Games202(P6、P7)环境光照与PRT全局光照
P6、实时环境光照 RealTime Environment Mapping
不同于全局光照
(1) IBL
我的Blog:
- QT with OpenGL(IBL-漫反射辐照)
- IBL-镜面反射(预滤波篇)
- IBL-镜面反射(LUT篇)
- QT with OpenGL(IBL-镜面反射)
(2) Spherical Harmonics 球面谐波
我的Blog:
- 球谐函数原理
- 球谐函数在环境光照中的使用原理
- 球谐函数实现环境光照漫反射实践
(3)Precomputed Radiance Transfer(PRT)【2002】
球谐函数近似环境光漫反射的问题:
- 没有几何遮挡关系,没有阴影。
- 只能处理Diffuse的物体
如何解决??引入了PRT。

PRT将Lighting部分拆成球面谐波基函数
L ( i ) ≈ ∑ l i B i ( i ) L(i)\approx \sum l_iB_i(i) L(i)≈∑liBi(i)
将light transport部分进行预计算,出射方向已知的情况下,light transport也可以展开维一个球面谐波函数。
V ( i ) ρ ( i , o ) m a x ( 0 , n ⋅ i ) ≈ ∑ t i B i ( i ) V(i)\rho(i,o)max(0,n\cdot i)\approx \sum t_iB_i(i) V(i)ρ(i,o)max(0,n⋅i)≈∑tiBi(i)
疑问:light transport与o(出射方向)无关,是不是代表着摄像机不可以转动?
- 并不是,因为物体只有漫反射,而漫反射向球面各个方向散射的光照是相同的,也就是说,同一个着色点在各个方向上看过去的颜色是相同的。故摄像机转动也不影响计算的结果!!!
疑问:那什么是不可以动的?
- light transport部分中包含了 V ( i ) V(i) V(i)项(可见性),也就是说一个着色点从四面八方是否被遮挡的条件是预计算好的。这标志这场景中进行预计算的物体,不可以再移动!
疑问:如果不变换环境光,是不是可以将 light transport 项和 lighting 项直接计算好值保存在着色点。这不就是给每个着色点预计算了所有的光照颜色吗?
- 额!我觉得确实是这样!!!不如离线渲染预计算~~
如果材质为Diffuse物体,即BRDF为常数
如果BRDF为常量,PRT可近似为如下函数,我们将光照与Visibility拆成两个积分分别计算(注意:这里并不是数学上严谨的,而是一种近似)

得到结果:
L ( o ) ≈ ρ ∑ l i ∫ Ω B i ( i ) V ( i ) m a x ( 0 , n ⋅ i ) d i L(o)\approx \rho \sum l_i \int_{\Omega} B_{i}(i)V(i)max(0,n\cdot i)di L(o)≈ρ∑li∫ΩBi(i)V(i)max(0,n⋅i)di
这里将光照的球谐函数留在了Visibility项中
∫ Ω B i ( i ) V ( i ) m a x ( 0 , n ⋅ i ) d i \int_{\Omega}B_{i}(i)V(i)max(0,n\cdot i)di ∫ΩBi(i)V(i)max(0,n⋅i)di
这里Light Transport项乘以一个基函数的积分,就是Light Transport的函数投影到基函数上的系数,这个系数可以预计算。
而预计算的结果就是Basic Function给数量的数字。即: ∫ Ω B i ( i ) V ( i ) m a x ( 0 , n ⋅ i ) d i \int_{\Omega}B_{i}(i)V(i)max(0,n\cdot i)di ∫ΩBi(i)V(i)max(0,n⋅i)di为一个预计算的常数
优点:光源可以切换,只要光源被预计算过
问题:场景中所有预计算过的东西都不能动
Light Transport的预计算
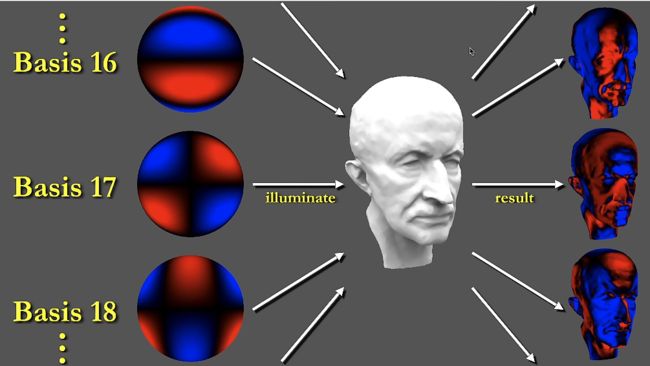
注意:这里是每一个 Shadering Point,也就是说,对于每一个着色顶点都要记录一串球谐函数展开的可见性系数(一般存储25个数,也就是5阶;更高的阴影精度需要存储更高阶的系数)
PRT既可以解决阴影问题,还可以解决Glossy的BRDF的问题。
渲染结果
将大量的渲染时间放在渲染之前,在渲染时只需要获取数据进行简单计算就好。该算法在2002年那个年代,就可以做到100帧的运行速率,可以说速度是非常快的。
如果材质为Glossy(有光泽的)物体,BRDF不为常数
Diffuse材质中提到,Light Transport项与出射方向无关,故是一个二维函数。
但Glossy物体BRDF不仅仅与入射角度有关,还与出射角度有关。也就是说它是一个4维的函数。

这里的i被预计算了,计算结果为 l i l_i li, T i ( o ) T_i(o) Ti(o)为预计算的与o有关的函数
然后我们将计算得到的 T i ( o ) T_i(o) Ti(o) 投影到关于 o o o 的球谐函数上。
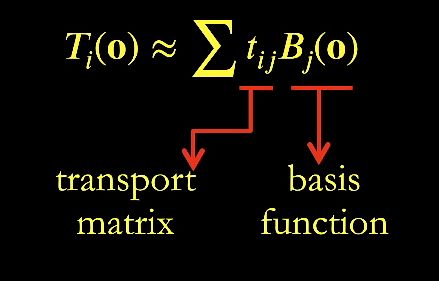
最终我们可以得到一个球谐函数的系数矩阵!!!

计算出射光照公式变为

将 L L L提出来得到
∑ i ( ∑ j t i j B j ( o ) ) L i \sum_i \left( \sum_j t_{ij}B_j(o) \right)L_i i∑(j∑tijBj(o))Li
我们已知,再Diffuse下,一个着色点保存了可见性函数的球谐函数系数。
而在Glossy下,一个着色点保存了与o有关的系数计算矩阵。
入射光照球谐系数与BRDF可见性矩阵相乘得到的向量 ∑ l i t i j \sum l_it_{ij} ∑litij,即为关于 o o o 的球谐函数的系数列表。

再将该系数与关于 o o o的基函数相乘求和,得到以o为出射角度的环境光镜面反射!
如果环境光照不变,我们可以将 light 项和 transport matrix项 直接计算好,得到一个关于o的基函数系数!
一般情况下,人们会使用3/4/5阶球谐基函数去近似。因此一个像素点需要存储 81/256/625 个系数
渲染结果
5万网格数,在2.2GHZ P4,ATI Radeon 8500上有3.6fps。
在现代GPU上,运行到100帧以上是没有问题的。
当金属度很高,反射接近于镜面时,PRT便解决不了这个问题了。

但到此为止,做的也仅仅是环境光照,直接光照的一种形式,而并不是有间接光照的全局光照。
PRT引入全局光照

经过了第一次的预计算,现在每一个着色点都记录了BRDF&visibility项在球谐函数下的展开系数,我们可以通过将着色点这些着色点作为次级光源再次预计算。
若我们将直接光照的计算表示为 L 1 L_1 L1:
L 1 ( x , ω ⃗ o ) = L e ( x , ω ⃗ o ) + ∫ Ω L ( x ′ , ω ⃗ i ) ρ ( x , ω ⃗ i , ω ⃗ o ) V ( x , x ′ ) G ( x , x ′ ) d ω ⃗ i L_1\left(x, \vec{\omega}_{o}\right)=L_{e}\left(x, \vec{\omega}_{o}\right)+\int_{\Omega} L\left(x^{\prime}, \vec{\omega}_{i}\right) \rho\left(x, \vec{\omega}_{i}, \vec{\omega}_{o}\right) V\left(x, x^{\prime}\right) G\left(x, x^{\prime}\right) d \vec{\omega}_{i} L1(x,ωo)=Le(x,ωo)+∫ΩL(x′,ωi)ρ(x,ωi,ωo)V(x,x′)G(x,x′)dωi
那么光线弹射一次得到的次级光照 L 2 L_2 L2计算即为
L 2 ( x , ω ⃗ o ) = ∫ Ω L 1 ( x ′ , ω ⃗ i ) ρ ( x , ω ⃗ i , ω ⃗ o ) ( 1 − V ( x , x ′ ) ) G ( x , x ′ ) d ω ⃗ i L_2\left(x, \vec{\omega}_{o}\right)=\int_{\Omega} L_1\left(x^{\prime}, \vec{\omega}_{i}\right) \rho\left(x, \vec{\omega}_{i}, \vec{\omega}_{o}\right) (1-V\left(x, x^{\prime}\right) )G\left(x, x^{\prime}\right) d \vec{\omega}_{i} L2(x,ωo)=∫ΩL1(x′,ωi)ρ(x,ωi,ωo)(1−V(x,x′))G(x,x′)dωi
而次级光照中,被照射的点为变为单个着色点,光源变为着色点周围可能会弹射直接光照的片元。
注意这里的差别:
L 2 L_2 L2中的visibility项变为了 1 − V ( x , x ′ ) 1-V(x,x') 1−V(x,x′)
这是因为次级光源正是来自那些被遮挡的部分。
次级光照计算的步骤
- 对于每个模型表面的着色点 x x x,计算他的直接光照(direct lighting)的传输函数 L 1 L_1 L1
- 从当前点 x x x 再发射多条射线,如果射线hit到其他三角形。
- 对于这个hit到的点,用三角形的重心坐标(barycentric coordinate)来对三角形每个顶点的transfer function的SH系数进行双线性插值求出hit点的transfer function的SH系数向量。
- 如果该点为Diffuse物体:则该系数为一个向量,可以直接得到SH系数向量
- 如果该点为Glossy物体:则该系数为一个矩阵,我们已知出射方向 o o o为该点指向渲染点的向量,故可以计算得到反射方向为 o o o的SH系数向量。
- 将得到的SH系数向量累加到着色点(次级光源照射点)
- 若着色点为Diffuse物体,则直接将两个球谐函数系数向量相加。
- 若着色点为Glossy物体,Glossy着色点存储了一个矩阵,因此我们需要将该球谐函数的向量与着色点的矩阵结合在一起,公式为【公式为自己推导,如果有错误,请指出纠正】:
∑ i [ ( ∑ j t i j B j ( o ) ) + t i 次 ] L i \sum_i \left[\left( \sum_j t_{ij}B_j(o) \right) + t_{i次} \right]L_i i∑[(j∑tijBj(o))+ti次]Li
设
t i 次 = ∑ j t i j 次 B j ( o ) t_{i次} = \sum_j t_{ij次}B_j(o) ti次=j∑tij次Bj(o)
这样我们就可以直接计算两个矩阵的和了
⇒ t i j 次 = ∫ t i 次 B j ( o ) = t i 次 ∫ o 在全部反射方向积分 B j ( o ) d ( o ) \Rightarrow t_{ij次} = \int t_{i次}B_j(o) \\ = t_{i次}\int_{o在全部反射方向积分}B_j(o) d(o) ⇒tij次=∫ti次Bj(o)=ti次∫o在全部反射方向积分Bj(o)d(o)
我们通过如下图可看到, B j B_j Bj 已知,对 B j ( o ) B_j(o) Bj(o) 球面积分。

结果是,只有第1项和第7项有值,且结果为一个常数,用 B B B表示。因此可以化简为
⇒ t i j 次 = t i 次 ∫ ( B 1 ( o ) + B 7 ( o ) ) d ( o ) = t i 次 B \Rightarrow t_{ij次} = t_{i次}\int (B_1(o)+B_7(o)) d(o) = t_{i次}B ⇒tij次=ti次∫(B1(o)+B7(o))d(o)=ti次B
综上得出:若着色点为Glossy物体,Glossy着色点存储的矩阵变化为
⇒ t i j 次 + = t i 次 B \Rightarrow t_{ij次} += t_{i次}B ⇒tij次+=ti次B
而这个B可近似为1。
本块内容参照了PRT完整讲解 https://zhuanlan.zhihu.com/p/609597945
并在其基础上 增加了 对于 Glossy物体 的 间接光反射 计算!
PRT的问题
- 场景中物体位置固定
- 物体的材质固定
- 需要大量的预计算
- 需要存储大量的数据
一些解决方法
- 使用其他的基函数(小波函数等)
- 将BRDF也单独求球谐函数,将方程变成三个基函数求和积分
- 不预计算,使用解析解解出来【在近10年内替代了PRT】
P7、全局光照
小波 Wavelet
将任意一个二维函数投影到小波对应的基函数上,可以发现大量的基函数的系数接近0.
这样我们就可以选取基函数中系数最大的多少个,做到有损压缩。
与SH(Spherical Harmonics )最大的区别是小波支持全频率的表示,既可以表示低频,也可以表示高频。
小波变换,对CubeMap中的每一个图单独做变换,将高频的信息留在周围三个区块,低频的东西留在左上图中。

然后对左上的图继续做小波变换,将高频取出,低频留在左上

SH与小波的区别
相同的存储量,小波可以得到更好的高频信息。
代价:小波不支持快速的旋转,不可以旋转光照。

RealTime Global Illumination(In 3D)实时全局光照(GI)
在实时全局光照中,一般指光线弹射两次的光照,即直接光照和一次的间接光照。
具体内容参照之后专题:
- Reflective Shadow Maps(RSM)
- Light Propagation Volumes(LPV)