高级数据结构之堆树
堆树
堆的定义
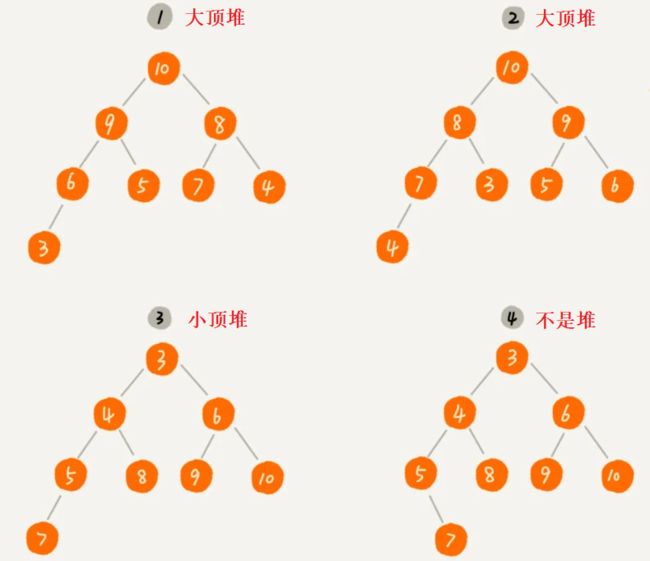
堆是什么?堆是一种特殊的树,他需要满足以下两点:
- 是一颗完全二叉树:除了最后一层,其他层每个节点都是满的且最后一层的节点都要靠左排列
- 其每一个节点的值都大于等于或者小于等于其左右子节点的值
堆实现思路
- 堆树如何来存储?
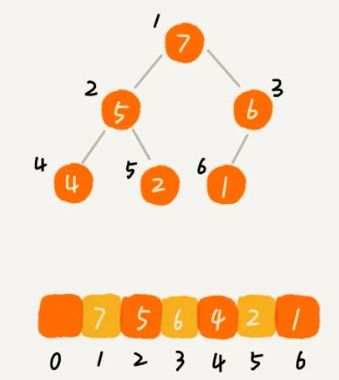
完全二叉树的最佳存储结构就是数组。因为它有着特殊的属性,直接利用下标就可以表示左右节点
左右子节点的公式:左=2i 、右=2i+1,i为数组下标
如果下标从0开始开始 ,这两个公式:2i+1,2i+2
- 堆的插入操作:
两种插入方式,头插法和尾插法,插入后可能不满足堆特性,调整过程称为堆化
头插法,从上往下堆化;尾插法:从下往上堆化
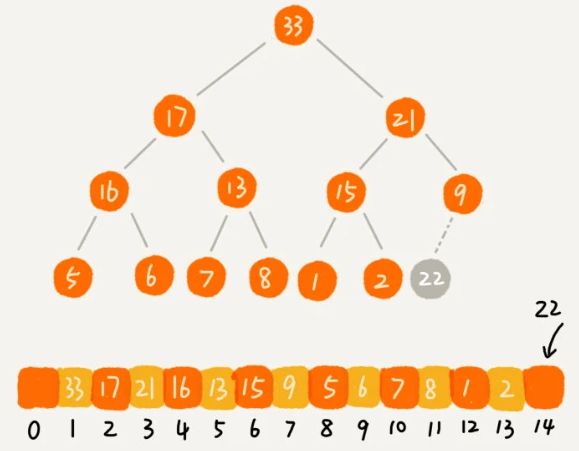
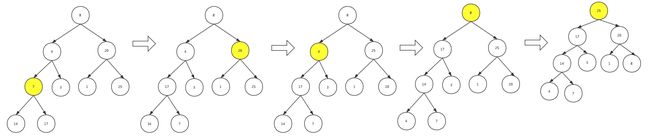
举例演示尾插法:从下往上堆化过程:
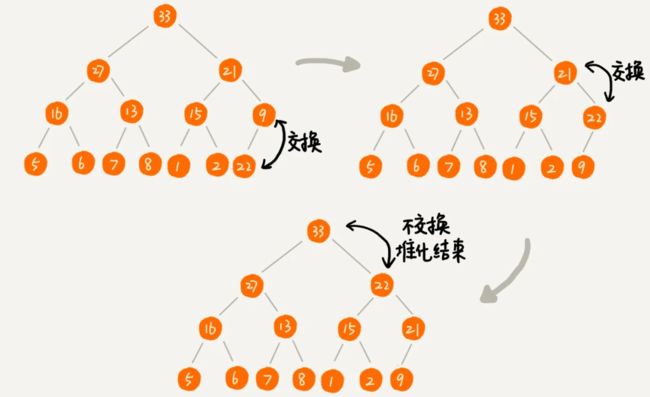
插入22
从下往上堆化
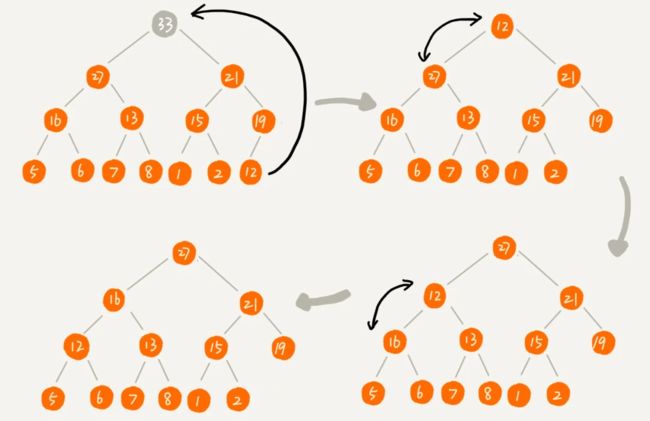
- 堆顶删除操作
其实就是把堆顶拿掉,然后进行堆化,怎么删除呢?
思路1:将数组第一个元素删除,整体迁移一位,然后堆化;
思路2:头尾交换,尾部位置指向null回收,然后堆化
对比:思路1需数组迁移复制,消耗大,思路2只需头尾交换
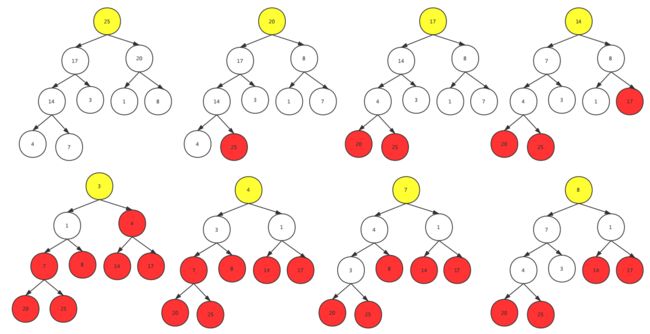
堆排序
假设给你一个序列:8 4 20 7 3 1 25 14 17,利用堆树进行排序
- 先按照序列顺序存储在完全二叉树中,然后堆化
- 头尾交换,保留尾节点数据,然后堆化
堆的应用
- 在前边实现赫夫曼树,我使用了一个优先队列大大减轻了我们的开发任务,但是大家知道这个优先队列内部是如何实现的呢?
- 如何实现一个用户热门搜索排行榜功能(微博热搜)?给你一个包含1亿关键词的用户检索的日志,如何取出排行前10的关键词。给你的处理机器:2CPU 2G内存 一台
Map分治+堆树
- 统计出现的频率Hash
- 维护一个大小为10的大顶堆
- 时间复杂度
- 空间复杂度。有可能内存爆炸,因为数据太多,放到硬盘
- 放到硬盘:分治,分成很多份。1亿个我分成 10个文件。分布式,分库分表。我要知道我的数据在哪张表,hash%分表数Hash%10=当前这个词放在哪个文件。分成了10个文件后:分别求top10,然后再把这个top10合起来。也就是有100个数,再求一次
- 优先级队列
- TOP K问题,比如给你一串1000万的数字 求前k大的数
一种是静态的数据
一种是动态的的数据
- 定时任务
- 给你1亿个不重复的数字(整数,1~2^32-1),求出top10。前10大的数字,还可动态添加新数字,但总个数不会超过1亿
实现优先队列
优先队列性质
- offer操作添加元素构建堆
- poll操作获取堆头并删除,然后堆化
- peek操作取堆头不删除
offer操作
// 添加一个元素
public boolean offer(E e) {
if (size == 0) queue[size++] = e;
else {
queue[size] = e;
bottomUpHeap(size, e);
//minHeap((E[]) queue, 0, size - 1);
size++;
grow(queue); // 扩容
}
return true;
}
自下而上堆化
/**
* 从下往上堆化, 时间复杂度:o(lgn)
* @param k 插入位置
* @param x 插入元素
*/
private void bottomUpHeap(int k, E x) {
while (k > 0) {
int parent = (k - 1) >>> 1; // 父节点
Object e = queue[parent];
// 插入>=父节点:小顶堆跳过
if (comparator.compare(x, (E) e) >= 0) break;
queue[k] = e;
k = parent;
}
queue[k] = x;
}
自上而下堆化
注意:经测试该段代码处理不了两个元素的堆化,poll删除操作有两个元素的处理逻辑
/**
* 自上而下堆化,时间复杂度:o(lgn)
* @param data 数据
* @param start 起始位置
* @param end 结束位置,主要用于堆排序
*/
private void upBottomHeap(E[] data, int start, int end) {
int p = start; // 父节点
int l = start * 2 + 1; // 左节点
int r = start * 2 + 2; // 右节点
while (l < end) {
// 满二叉树,没有最后一个右节点
if (r >= end && comparator.compare(data[p], data[l]) < 0) break;
if (r < end && // 满二叉树,有最后一个右节点.父节点 大于两个子节点 无需交换位置
comparator.compare(data[p], data[l]) < 0 &&
comparator.compare(data[p], data[r]) < 0) return; // 不用交换
// 比较子节点,小的一个和父节点交换位置
int swapIndex = r;
if (r < end && comparator.compare(data[l], data[r]) < 0) { // 左边比右边小
swapIndex = l; // 就要换右节点跟父节点
}
// 交换
swap(data, p, swapIndex);
// 循环模拟递归,记录下次递归位置
p = swapIndex; // 继续堆化
l = p * 2 + 1;
r = p * 2 + 2;
}
}
poll操作
public E poll() {
if (size == 0) return null;
E e = (E) queue[0];
removeTailHeap(); // 头尾交换,堆化
// removeHeadHeap(); // 删除头节点堆化
return e;
}
removeTailHeap(); // 头尾交换,堆化
private void removeTailHeap() {
// 交换头尾,然后堆化
swap((E[]) queue, 0, --size);
//queue[size]=null; // 回收数据,不回收就是堆排序
upBottomHeap((E[]) queue, 0, size - 1);
// 处理还有两个元素的特殊情况
if (size == 2 && comparator.compare((E) queue[0], (E) queue[1]) > 0) {
swap((E[]) queue, 0, 1);
}
}
removeHeadHeap(); // 删除头节点堆化
private void removeHeadHeap() {
queue = Arrays.copyOfRange(queue, 1, queue.length);
upBottomHeap((E[]) queue, 0, --size);
}
完整代码
package datastructure.queue;
import java.util.AbstractQueue;
import java.util.Arrays;
import java.util.Comparator;
import java.util.Iterator;
/**
* 优先队列
*
* @author zw
* @create 2023-04-14 23:21
*/
public class MyPriorityQueue<E> extends AbstractQueue<E> {
private final double DILATANCY_FACTOR = 0.75d;
private final Comparator<? super E> comparator; // 比较器决定是大顶堆还是小顶堆
transient Object[] queue;
private int size = 0;
public MyPriorityQueue(Comparator<? super E> comparator) {
this.queue = new Object[16];
this.comparator = comparator;
}
@Override
public Iterator<E> iterator() {
return null;
}
@Override
public int size() {
return size;
}
@Override
public boolean isEmpty() {
return size == 0;
}
// 添加一个元素
@Override
public boolean offer(E e) {
if (size == 0) queue[size++] = e;
else {
queue[size] = e;
bottomUpHeap(size, e);
//upBottomHeap((E[]) queue, 0, size - 1);
size++;
grow(queue);
}
return true;
}
private void grow(Object[] data) {
if (size > queue.length * DILATANCY_FACTOR) {
// 扩容,会把size*2
int newSize = size << 1 + 1;
queue = Arrays.copyOf(data, newSize);
}
}
private void swap(E[] data, int p1, int p2) {
E temp = data[p1];
data[p1] = data[p2];
data[p2] = temp;
}
// 移除并返问队列头部的元素
/**
* 两种方式:
* 1、头尾交换,删除尾节点,堆化
* 2、删除头节点,然后堆化
*
* @return
*/
@Override
public E poll() {
if (size == 0) return null;
E e = (E) queue[0];
//System.out.println(String.format("取出%s,堆化前%s", e, Arrays.toString(queue)));
removeTailHeap();
//System.out.println(String.format("取出%s,堆化后%s", e, Arrays.toString(queue)));
return e;
}
/**
* 这种方式要删除位置,但是思路简单
*/
private void removeHeadHeap() {
queue = Arrays.copyOfRange(queue, 1, queue.length);
upBottomHeap((E[]) queue, 0, --size);
}
/**
* 这种方式位置保留
*/
private void removeTailHeap() {
// 交换头尾,然后堆化
swap((E[]) queue, 0, --size);
//queue[size]=null; // 回收数据,是否注释,打印结果有不同理解
//System.out.println(String.format("头尾交换%s", Arrays.toString(queue)));
upBottomHeap((E[]) queue, 0, size - 1);
if (size == 2 && comparator.compare((E) queue[0], (E) queue[1]) > 0) {
swap((E[]) queue, 0, 1);
}
}
// 返回队列头部的元素
@Override
public E peek() {
if (size == 0) return null;
size--;
return (E) queue[0];
}
/**
* 插入过程堆化:从下往上,交换,直到根
*
* @param k 插入位置
* @param x 插入元素
*/
private void bottomUpHeap(int k, E x) {
while (k > 0) {
int parent = (k - 1) >>> 1; // 父节点
Object e = queue[parent];
// 插入>=父节点:小顶堆跳过
if (comparator.compare(x, (E) e) >= 0) break;
queue[k] = e;
k = parent;
}
queue[k] = x;
}
/**
* 小顶堆化
*
* @param data 数据
* @param start 起始位置
* @param end 结束位置,主要用于堆排序
*/
private void upBottomHeap(E[] data, int start, int end) {
int p = start; // 父节点
int l = start * 2 + 1; // 左节点
int r = start * 2 + 2; // 右节点
while (l < end) {
// 满二叉树,没有最后一个右节点
if (r >= end && comparator.compare(data[p], data[l]) < 0) break;
if (r < end && // 满二叉树,有最后一个右节点.父节点 大于两个子节点 无需交换位置
comparator.compare(data[p], data[l]) < 0 &&
comparator.compare(data[p], data[r]) < 0) return; // 不用交换
// 比较子节点,小的一个和父节点交换位置
int swapIndex = r;
if (r < end && comparator.compare(data[l], data[r]) < 0) { // 左边比右边小
swapIndex = l; // 就要换右节点跟父节点
}
// 交换
swap(data, p, swapIndex);
// 循环模拟递归,记录下次递归位置
p = swapIndex; // 继续堆化
l = p * 2 + 1;
r = p * 2 + 2;
}
}
// 堆排序
private void upBottomHeap(E[] data) {
int len = data.length;
for (int i = len / 2 - 1; i >= 0; i--) { //o(nlgn)
maxHeap(data, i, len); //
}
for (int i = len - 1; i > 0; i--) { //o(nlgn)
swap(data, 0, i);
upBottomHeap(data, 0, i); //这个i能不能理解?因为len~i已经排好序了
}
}
}
测试用例
public static void main(String[] args) {
MyPriorityQueue<Integer> queue = new MyPriorityQueue<>((o1, o2) -> o1 - o2);
Integer[] datas = {8, 4, 20, 7, 3, 1, 25, 14, 17};
System.out.println("输入:" + Arrays.toString(datas));
queue.heapSort(datas);
System.out.println("堆排序结果:" + Arrays.toString(datas));
Integer[] datas2 = {8, 4, 20, 7, 3, 1, 25, 14, 17};
for (int data : datas2) {
queue.offer(data);
System.out.println(String.format("插入%s,堆化后%s", data, Arrays.toString(queue.queue)));
}
System.out.println("---------------------");
while (!queue.isEmpty()) {
Integer poll = queue.poll();
System.out.println(String.format("取出%s,size=%s,堆化后%s", poll, queue.size, Arrays.toString(queue.queue)));
}
}
运行结果
输入:[8, 4, 20, 7, 3, 1, 25, 14, 17]
堆排序结果:[25, 20, 17, 14, 8, 7, 4, 3, 1]
插入8,堆化后[8, null, null, null, null, null, null, null, null, null, null, null, null, null, null, null]
插入4,堆化后[4, 8, null, null, null, null, null, null, null, null, null, null, null, null, null, null]
插入20,堆化后[4, 8, 20, null, null, null, null, null, null, null, null, null, null, null, null, null]
插入7,堆化后[4, 7, 20, 8, null, null, null, null, null, null, null, null, null, null, null, null]
插入3,堆化后[3, 4, 20, 8, 7, null, null, null, null, null, null, null, null, null, null, null]
插入1,堆化后[1, 4, 3, 8, 7, 20, null, null, null, null, null, null, null, null, null, null]
插入25,堆化后[1, 4, 3, 8, 7, 20, 25, null, null, null, null, null, null, null, null, null]
插入14,堆化后[1, 4, 3, 8, 7, 20, 25, 14, null, null, null, null, null, null, null, null]
插入17,堆化后[1, 4, 3, 8, 7, 20, 25, 14, 17, null, null, null, null, null, null, null]
---------------------
取出1,size=8,堆化后[3, 4, 17, 8, 7, 20, 25, 14, 1, null, null, null, null, null, null, null]
取出3,size=7,堆化后[4, 7, 17, 8, 14, 20, 25, 3, 1, null, null, null, null, null, null, null]
取出4,size=6,堆化后[7, 8, 17, 25, 14, 20, 4, 3, 1, null, null, null, null, null, null, null]
取出7,size=5,堆化后[8, 20, 17, 25, 14, 7, 4, 3, 1, null, null, null, null, null, null, null]
取出8,size=4,堆化后[14, 20, 17, 25, 8, 7, 4, 3, 1, null, null, null, null, null, null, null]
取出14,size=3,堆化后[17, 20, 25, 14, 8, 7, 4, 3, 1, null, null, null, null, null, null, null]
取出17,size=2,堆化后[20, 25, 17, 14, 8, 7, 4, 3, 1, null, null, null, null, null, null, null]
取出20,size=1,堆化后[25, 20, 17, 14, 8, 7, 4, 3, 1, null, null, null, null, null, null, null]
取出25,size=0,堆化后[25, 20, 17, 14, 8, 7, 4, 3, 1, null, null, null, null, null, null, null]
实现top k问题
实际问题抽象画:TOP K问题,比如给你一串1000万的数字 求前k大的数,两种情况
一种是静态的数据
一种是动态的的数据
- 给你1亿个不重复的数字(整数,1~2^32-1),求出top10。前10大的数字,还可动态添加新数字,但总个数不会超过1亿
- 如何实现一个用户热门搜索排行榜功能(微博热搜)?给你一个包含1亿关键词的用户检索的日志,如何取出排行前10的关键词。给你的处理机器:2CPU 2G内存 一台
Map分治+堆树
- 统计出现的频率Hash
- 维护一个大小为10的大顶堆
- 时间复杂度
- 空间复杂度。有可能内存爆炸,因为数据太多,放到硬盘
- 放到硬盘:分治,分成很多份。1亿个我分成 10个文件。分布式,分库分表。我要知道我的数据在哪张表,hash%分表数Hash%10=当前这个词放在哪个文件。分成了10个文件后:分别求top10,然后再把这个top10合起来。也就是有100个数,再求一次
package leetcode;
import datastructure.queue.MyPriorityQueue;
import java.io.*;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
/**
* 如何实现一个用户热门搜索排行榜功能(微博热搜)?给你一个包含1亿关键词的用户检索的日志,如何取出排行前10的关键词,还可动态添加新数字。
* 给你的处理机器:2CPU 2G内存 一台
*
* @author zw
* @create 2023-04-15 23:18
*/
public class TopK {
private List<String> fileSegments = new ArrayList<>();
/**
* 统计词频
*
* @param filePath
* @return
* @throws Exception
*/
private Map<String, Integer> wordCount(String filePath) throws Exception {
Map<String, Integer> wordCountMap = new HashMap<>();
InputStreamReader isr = new InputStreamReader(new FileInputStream(filePath), "UTF-8");
BufferedReader br = new BufferedReader(isr);
String str = null;
while ((str = br.readLine()) != null) {
String word = String.valueOf(str);
if (wordCountMap.containsKey(word)) {
wordCountMap.put(word, wordCountMap.get(word) + 1);
} else {
wordCountMap.put(word, 1);
}
}
return wordCountMap;
}
/**
* 数据文件分片
*
* @param filePath 文件路径
* @param num 分段数
*/
private void fileSegment(String filePath, int num) throws Exception {
File file = new File(filePath);
String name = file.getName().split(".")[0];
String suffix = file.getName().split(".")[1];
InputStreamReader isr = new InputStreamReader(new FileInputStream(filePath), "UTF-8");
BufferedReader br = new BufferedReader(isr);
String str = null;
while ((str = br.readLine()) != null) {
String word = String.valueOf(str);
int segment = word.hashCode() % num;
// 写到分片文件中
String segmentFilePath = file.getParent() + "/" + name + "_" + segment + "." + suffix;
writeSegmentFile(word, segmentFilePath);
}
}
private void writeSegmentFile(String word, String segmentFilePath) throws Exception {
File writeFile = new File(segmentFilePath);
if (!writeFile.exists()) {
// // 文件不存在,创建
writeFile.createNewFile();
fileSegments.add(segmentFilePath);
}
// 写入文件末尾行
BufferedWriter writer = new BufferedWriter(new FileWriter(writeFile));
writer.write(word);
writer.newLine();
}
public static void main(String[] args) throws Exception {
MyPriorityQueue<Map.Entry<String, Integer>> priorityQueue =
new MyPriorityQueue<Map.Entry<String, Integer>>(10, (o1, o2) -> o1.getValue() - o2.getValue());
TopK topK = new TopK();
// 数据分片
topK.fileSegment("E:\\userhost.txt", 10);
// 统计每个分段top k
for (String fileSegment : topK.fileSegments) {
MyPriorityQueue<Map.Entry<String, Integer>> segmentPriorityQueue =
new MyPriorityQueue<Map.Entry<String, Integer>>(10, (o1, o2) -> o1.getValue() - o2.getValue());
Map<String, Integer> wordCountMap = topK.wordCount(fileSegment);
for (Map.Entry<String, Integer> entry : wordCountMap.entrySet()) {
segmentPriorityQueue.offer(entry);
}
while (!segmentPriorityQueue.isEmpty()) {
priorityQueue.offer(segmentPriorityQueue.poll());
}
}
while (!priorityQueue.isEmpty()) {
Map.Entry<String, Integer> poll = priorityQueue.poll();
System.out.println(String.format("关键字=%s,词频=%s", poll.getKey(), poll.getValue()));
}
}
}