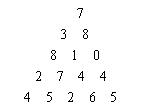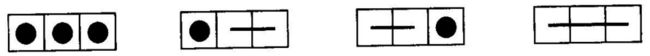OJ刷题 第十四篇(递归较多)
23204 - 进制转换
时间限制 : 1 秒
内存限制 : 128 MB
将一个10进制数x(1 <= x <= 100,000,000)转换成m进制数(2<= m <= 16) 。分别用 ABCDEF表示10以上的数字。
输入
x m (1 <= x <= 100,000,000, 2<= m <= 16)
输出
m进制数
样例
输入
31 16
输出
1F
答案:
#include
using namespace std;
int main() {
int x, m;
cin >> x >> m;
char arr[17] = { '0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F'};
char s[32] = { 0 };
int length = 0;
while (x) {
int r = x % m;
s[length++] = arr[r];
x /= m;
}
for (int i = length - 1; i >= 0; i--) {
cout << s[i];
}
return 0;
} 分析:这道题在刚学C语言或者数据结构栈那里来写是比较难的,因为栈的一个应用就是可以用来求进制转换。由于这道题是2到16进制之间任意进制的转换,因此我们要定义一个数组用来表示每次取模后的字符。并初始化,比如本题中的arr数组,先递增存储,最后倒着打印即可。
本题难的地方就是构造那个arr数组用来存储每次取模后的的字符。最后要倒着打印,刚开始学C语言感觉这题很难,但是现在感觉就基础题!
是否通过:
31001 - 数字三角形(动态规划思想)
时间限制 : 1 秒
内存限制 : 128 MB
如下所示为一个数字三角形。请编一个程序计算从顶到底的某处的一条路径,使该路径所经过的数字总和最大。只要求输出总和。
- 一步可沿左斜线向下或右斜线向下走;
- 三角形行数小于等于100;
- 三角形中的数字为0,1,…,99。
输入
测试数据通过键盘逐行输入
输出
最大值
样例
输入
5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5
输出
30
答案:
#include
using namespace std;
int main() {
int n;
int a[101][101] = { 0 };
cin >> n;
//输入数据,从下标1开始,对本题计算大有帮助
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
cin >> a[i][j];
}
}
//计算
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
int max1 = a[i][j] + a[i - 1][j - 1];
int max2 = a[i][j] + a[i - 1][j];
int max = max1 > max2 ? max1 : max2;
a[i][j] = max;
}
}
//找最大值路径
int MAX = a[n][1];
for (int i = 2; i <= n; i++) {
MAX = MAX > a[n][i] ? MAX : a[n][i];
}
cout << MAX << endl;
return 0;
} 分析:这个题其实难度不算大,只是题目有点难度的思维逻辑。题目说到:
一步可沿左斜线向下或右斜线向下走
这个是什么意思呢?意思就是说对每个元素a[i][j],到这个元素的路径只能从两个地方得来:
1、加上a[i-1][j-1],得到一个路径值
2、加上a[i-1][j],得到一个路径值
每个点都只有这两种情况,然后选出值较大的那个作为这个点的路径值。直到算到最后一行,然后找出最后一行的最大值即可。
是否通过:
31002 - 走楼梯
时间限制 : 1 秒
内存限制 : 128 MB
楼梯有 N 级台阶,上楼可以一步上一阶,也可以一步上二阶。编一递归程序,计算共有多少种不同走法?
输入
一个整数,表示 N 级台阶
输出
整数,表示走法的数量
样例
输入
3
输出
3
答案:
#include
using namespace std;
int f1(int N) {
if (N == 1) {
return 1;
}
if (N == 2) {
return 2;
}
return f1(N - 2) + f1(N - 1);
}
int main() {
int N;
cin >> N;
int count = f1(N);
cout << count << endl;
return 0;
} 分析:这是初学C语言遇到的最多的问题,也是一个非常经典的问题。它的核心思想就是
f3=f1+f2
一般能不用递归就不用,因为递归会消耗栈,问题规模大了,会重复计算很多,浪费时间。
是否通过:
31003 - 兔子繁殖
时间限制 : 1 秒
内存限制 : 128 MB
有一种兔子,出生后一个月就可以长大,然后再过一个月一对长大的兔子就可以生育一对小兔子且以后每个月都能生育一对。现在,我们有一对刚出生的这种兔子,那么,n 个月过后,我们会有多少对兔子呢?假设所有的兔子都不会死亡。
输入
输入文件仅一行,包含一个自然数 n。
输出
输出文件仅一行,包含一个自然数,即 n 个月后兔子的对数。
样例
输入
5
输出
5
#include
using namespace std;
int main() {
int n;
cin >> n;
long long sum = 0;
if (n == 1 || n == 2) {
sum = 1;
}
else {
long long int f1 = 1, f2 = 1;
for (int i = 3; i <= n; i++) {
sum = f1 + f2;
f2 = f1;
f1 = sum;
}
}
cout << sum << endl;
return 0;
} 分析:兔子繁殖问题就是一个著名的斐波那契数列。同样可以用递归,但是这里我没有用递归,性能会大幅度提高。
是否通过:
31004 - 骨牌铺法 (进阶版递归,二刷!!)
时间限制 : 1 秒
内存限制 : 128 MB
有 1×n 的一个长方形,用一个 1×1、1×2 和 1×3 的骨牌铺满方格。例如当 n=3 时为 1×3 的方格。
此时用 1×1、1×2 和 1×3 的骨牌铺满方格,共有四种铺法。如下图:
输入
n
输出
一共有多少种铺法
样例
输入
3
输出
4
答案:
#include
using namespace std;
int main() {
int n;
cin >> n;
int sum = 0;
if (n == 1) {
sum = 1;
}
else if (n == 2) {
sum = 2;
}
else if (n == 3) {
sum = 4;
}
else {
int f1 = 1, f2 = 2, f3 = 4;
for (int i = 4; i <= n; i++) {
sum = f1 + f2 + f3;
f1 = f2;
f2 = f3;
f3 = sum;
}
}
cout << sum << endl;
return 0;
} 分析:这个题第一次遇到感觉难度非常大,一是觉得题目生疏很难,或者说没理解题目的意思。我们先来整理题目的意思,当然我们知道
如果是1*1的矩形,只有 1种填充方法
如果是1*2的矩形,有2种填充方法,一种是全部用1*1方形填充,一种是一个用1*2方形填充
如果是1*3的矩形,有4种填充,怎么算?一种是全部用1*1的填充,一种是前面一个位置用1*1的方形填充,后面两个位置用1*2的方形填充,一种是前面两个位置用1*2的填充,后面一个位置用1*1的填充,最后一种就是直接用1*3的填充。
如果是1*4的矩阵,那么第一个位置用1*1的方形填充,后面三个位置任意填充有4种,前面两个位置用1*2的方形填充,后面两个位置有2种,前面三个位置用1*3的方形填充,后面一个位置有1种,即公有1+2+4=7种。
我想到这里已经发现了,骨牌铺法也是一个递归问题,相比斐波那契数列,这个题深度更深
f4=f3+f2+f1
是否通过:
23207 - 五子棋(重点!!二刷!)
时间限制 : 1 秒
内存限制 : 128 MB
五子棋是世界智力运动会竞技项目之一,是一种两人对弈的纯策略型棋类游戏,通常双方分别使用黑白两色的棋子,下在棋盘直线与横线的交叉点上,先形成5子连线者获胜。如果要开发一款五子棋小游戏,判断棋局输赢也将是其中很重要的一部分。
现有一个n行m列的棋盘,我们使用1表示棋格里有黑色棋子,2表示棋格里有白色棋子,0表示没有棋子。 给定t场对弈棋局,请判断是否有5子连线的棋子,如果有则输出Yes,没有则输出No。
输入
第1行,n m t (1≤n、m≤100,1≤t≤10) 接下来共t组数据,每行组数据n行,每行m个整数,每个整数的取值为0、1或者2
输出
t 行,如果有5子连线的棋子则输出Yes,否则输出No。每行一个。
样例
输入
5 6 4 1 1 1 1 1 0 2 2 0 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 1 1 0 1 0 2 1 0 2 2 0 0 1 0 2 0 0 0 1 0 2 0 0 0 1 0 2 0 0 2 1 1 0 1 0 0 2 0 2 2 0 0 1 0 1 0 0 0 0 0 2 0 0 0 1 0 2 0 1 2 1 1 0 1 2 2 1 0 2 2 0 0 1 0 2 0 0 0 1 2 2 0 0 0 2 0 2 0 0
输出
Yes Yes No Yes
答案:
#include
using namespace std;
bool Check(int a[][200], int n, int m) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (a[i][j] != 0) {
//判断右横
if (j + 4 <= m &&
a[i][j] == a[i][j+1] &&
a[i][j] == a[i][j+2] &&
a[i][j] == a[i][j+3] &&
a[i][j] == a[i][j+4]) {
return true;
}
//判断下竖
if (i + 4 <= n &&
a[i][j] == a[i+1][j] &&
a[i][j] == a[i+2][j] &&
a[i][j] == a[i+3][j] &&
a[i][j] == a[i+4][j]) {
return true;
}
//判断右斜
if (j + 4 <= m && i + 4 <= n &&
a[i][j] == a[i+1][j+1] &&
a[i][j] == a[i+2][j+2] &&
a[i][j] == a[i+3][j+3] &&
a[i][j] == a[i+4][j+4]) {
return true;
}
//判断左斜
if (j >= 5 && i + 4 <= n &&
a[i][j] == a[i+1][j-1] &&
a[i][j] == a[i+2][j-2] &&
a[i][j] == a[i+3][j-3] &&
a[i][j] == a[i+4][j-4]) {
return true;
}
}
}
}
return false;
}
int main() {
int n, m, t;
int a[200][200];
cin >> n >> m >> t;
for (int k = 1; k <= t; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cin >> a[i][j];
}
}
if (Check(a, n, m)) {
cout << "Yes" << endl;
}
else {
cout << "No" << endl;
}
}
} 分析:虽然很多人下过五子棋也知道下棋规则,但是要写代码判断一个棋局是不是分出胜负还是有不小难度的。五子棋游戏这是一款经典游戏,之前也开发来玩过。我们在判断的时候不用判断所有棋子,我们只需判断部分棋子就可以知道胜负,分四种情况:
1、右横,即某一行有5个棋子即可,只需判断最后一个棋子不超过棋盘的列数即可,即j+4<=m
2、下竖,即某一列有5个棋子即可,只需判断最后一个棋子的行数不超过棋盘的行数即可,即i+4<=n
3、右斜,即主对角线方向有5个棋子,两个条件,因为是斜着向右下方,因此j+4<=m且i+4<=n
4、左斜,即副对角线方向有5个棋子,同样是两个条件,因为是斜着向左下方,因此i+4<=n且j-4>=1,即只需j>=5即可!
是否通过: