代码随想录算法训练营第三天|链表part01|203.707.06
2023/7/28 任务
链表理论基础，203.移除链表元素，707.设计链表，06.反转链表
链表理论基础
链表的定义
-
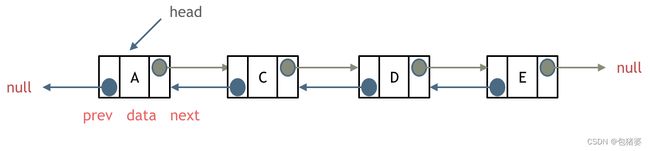
链表是一种通过指针串联在一起的线性结构，（以单链表为例）每一个节点由两部分组成，一个是数据域一个是指针域（存放指向下一个节点的指针），最后一个节点的指针域指向null（空指针的意思）。
-
链表的入口节点称为链表的头结点也就是head。
public class ListNode {
// 结点的值
int val;
// 下一个结点
ListNode next;
// 节点的构造函数(有一个参数)
public ListNode(int val) {
this.val = val;
}
}
链表的类型
-
单链表
- 指针域只能指向节点的下一个节点。
-
双链表
- 每一个节点有两个指针域，一个指向下一个节点，一个指向上一个节点。
- 既可以向前查询也可以向后查询。
-
循环链表
- 链表首尾相连，可以用来解决约瑟夫环问题。
- 链表首尾相连，可以用来解决约瑟夫环问题。
链表在内存中的存储方式
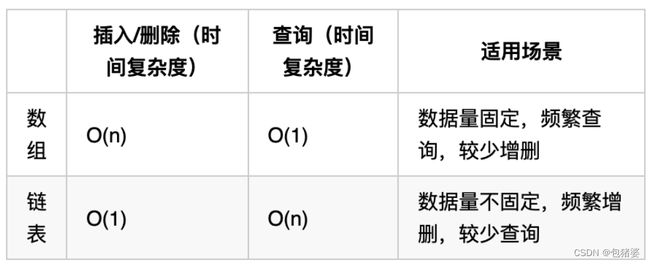
数组是在内存中是连续分布的，但是链表在内存中不是连续分布的。
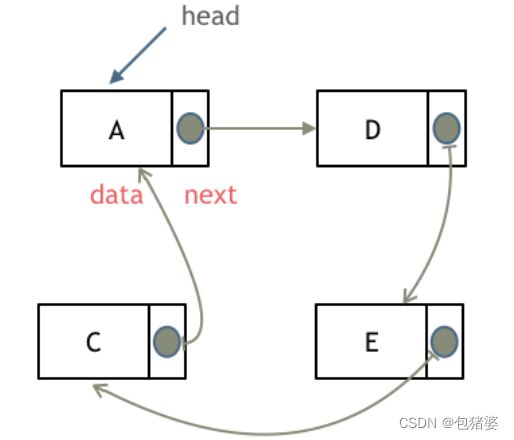
链表是通过指针域的指针链接在内存中各个节点。
所以链表中的节点在内存中不是连续分布的 ，而是散乱分布在内存中的某地址上，分配机制取决于操作系统的内存管理。
链表的操作
-
删除节点
如删除D节点，只需将C节点的next指针指向E节点即可。
在链表中删除后，D节点仍然存在内存中。在C++中最好手动释放它，而Java、Python中有内存回收机制。 -
添加节点
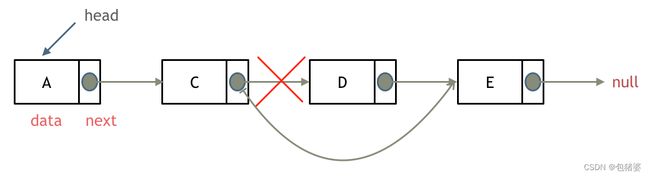
链表的增添和删除都是O(1)操作，也不会影响到其他节点。
但是要注意，要是删除第五个节点，需要从头节点查找到第四个节点通过next指针进行删除操作，查找的时间复杂度是O(n)。
链表与数组的性能分析
203.移除链表元素
链表操作中，可以使用原链表来直接进行删除操作，也可以设置一个虚拟头结点再进行删除操作。
题目链接/文章讲解/视频讲解
（解法一）直接使用原来的链表
class Solution {
public ListNode removeElements(ListNode head, int val) {
// 头节点判断
while (head != null && head.val == val) {
head = head.next;
}
if (head == null) {
return head;
}
ListNode cur = head;
while (cur != null) {
while (cur.next != null && cur.next.val == val) {
cur.next = cur.next.next;
}
cur = cur.next;
}
return head;
}
}
时间复杂度: O(n)
空间复杂度: O(1)
在单链表中移除头结点和移除其他节点的操作方式是不一样的，可以设置一个虚拟头结点，这样原链表的所有节点就都可以按照统一的方式进行移除了。
（解法二）设置虚拟头节点dummyHead
（和解法一的大致区别是 将头节点额外判断的代码去掉了，新加了dummy节点指向head，cur初始等于dummy，最后返回的是实际的头节点dummy->next）
下段代码在切入点转变的基础上，又加入了一个变量表示pre。
class Solution {
public ListNode removeElements(ListNode head, int val) {
if (head == null) {
return head;
}
ListNode dummy = new ListNode(-1, head);
ListNode pre = dummy;
ListNode cur = head;
while (cur != null) {
if (cur.val == val) {
pre.next = cur.next;
} else {
pre = cur;
}
cur = cur.next;
}
return dummy.next;
}
}
时间复杂度: O(n)
空间复杂度: O(1)
707.设计链表
使用虚拟头结点
题目链接/文章讲解/视频讲解
// 单链表
class ListNode {
int val;
ListNode next;
ListNode(int val) {
this.val = val;
}
}
class MyLinkedList {
// size存储链表元素的个数
int size;
// 虚拟头结点
ListNode head;
// 初始化链表
public MyLinkedList() {
size = 0;
head = new ListNode(0);
}
public int get(int index) {
if (index >= size || index < 0) {
return -1;
}
ListNode cur = head;
for (int i = 0; i <= index; i++) {
cur = cur.next;
}
return cur.val;
}
public void addAtHead(int val) {
addAtIndex(0, val);
}
public void addAtTail(int val) {
addAtIndex(size, val);
}
public void addAtIndex(int index, int val) {
if (index > size) {
return;
}
if (index < 0) {
index = 0;
}
ListNode addNode = new ListNode(val);
ListNode pre = head;
for (int i = 0; i < index; i++) {
pre = pre.next;
}
addNode.next = pre.next;
pre.next = addNode;
size++;
}
public void deleteAtIndex(int index) {
if (index < 0 || index >= size) {
return;
}
ListNode pre = head;
for (int i = 0; i < index; i++) {
pre = pre.next;
}
pre.next = pre.next.next;
size--;
}
}
// 双链表
// 除了定义的区别，代码部分最大的不同在get方法中，多了判断从头还是尾去get。此外要注意prev和next都需要修改。
// 写的时候犯了个错误，让pre.next = pre.next.next后，想继续pre.next.next.prev操作原来没改时候的pre.next的next，所以出现了错误，应该变为pre.next.prev。
class ListNode {
int val;
ListNode prev;
ListNode next;
ListNode(int val) {
this.val = val;
}
}
class MyLinkedList {
int size;
ListNode head;
ListNode tail;
public MyLinkedList() {
size = 0;
head = new ListNode(0);
tail = new ListNode(0);
head.next = tail;
tail.prev = head;
}
public int get(int index) {
if (index >= size || index < 0) {
return -1;
}
// 判断从哪一边开始遍历 时间更短
ListNode cur = tail;
if (index >= size / 2) {
for (int i = size; i > index; i--) {
cur = cur.prev;
}
} else {
cur = head;
for (int i = 0; i <= index; i++) {
cur = cur.next;
}
}
return cur.val;
}
public void addAtHead(int val) {
addAtIndex(0, val);
}
public void addAtTail(int val) {
addAtIndex(size, val);
}
public void addAtIndex(int index, int val) {
if (index > size) {
return;
}
if (index < 0) {
index = 0;
}
ListNode addNode = new ListNode(val);
ListNode pre = head;
for (int i = 0; i < index; i++) {
pre = pre.next;
}
addNode.next = pre.next;
addNode.prev = pre;
pre.next.prev = addNode;
pre.next = addNode;
size++;
}
public void deleteAtIndex(int index) {
if (index < 0 || index >= size) {
return;
}
ListNode pre = head;
for (int i = 0; i < index; i++) {
pre = pre.next;
}
pre.next = pre.next.next;
pre.next.prev = pre;
size--;
}
}
时间复杂度: 涉及 index 的相关操作为 O(index), 其余为 O(1)
空间复杂度: O(n)
206.反转链表
题目链接/文章讲解/视频讲解
改变所有next指针的指向即可。
// 双指针法
class Solution {
public ListNode reverseList(ListNode head) {
ListNode pre = null;
ListNode cur = head;
ListNode nex;
while (cur != null) {
// 先保存cur的next
nex = cur.next;
// 进行反转
cur.next = pre;
// 移动，为下一次做准备
pre = cur;
cur = nex;
}
head = pre;
return head;
}
}
时间复杂度: O(n)
空间复杂度: O(1)
// 递归法
class Solution {
public ListNode reverseList(ListNode head) {
head = reverse(head, null);
return head;
}
public ListNode reverse(ListNode cur, ListNode pre) {
if (cur == null) {
return pre;
}
ListNode nex = cur.next;
cur.next = pre;
return reverse(nex, cur);
}
}
// 从后向前递归
class Solution {
ListNode reverseList(ListNode head) {
// 边缘条件判断
// 当head是正序的最后一个节点时，递归开始返回，从此last一直记录这个反转后的头节点
if (head.next == null) return head;
// 递归调用，翻转第二个节点开始往后的链表
ListNode last = reverseList(head.next);
// 除了last记录的节点不需要走这些步骤，其他节点都需要做：下个节点指向自己，自己指向空
head.next.next = head;
// 最后能够保证 ： 此时的 head 节点为尾节点，next 需要指向 NULL
head.next = null;
return last;
}
}
时间复杂度: O(n), 要递归处理链表的每个节点
空间复杂度: O(n), 递归调用了 n 层栈空间