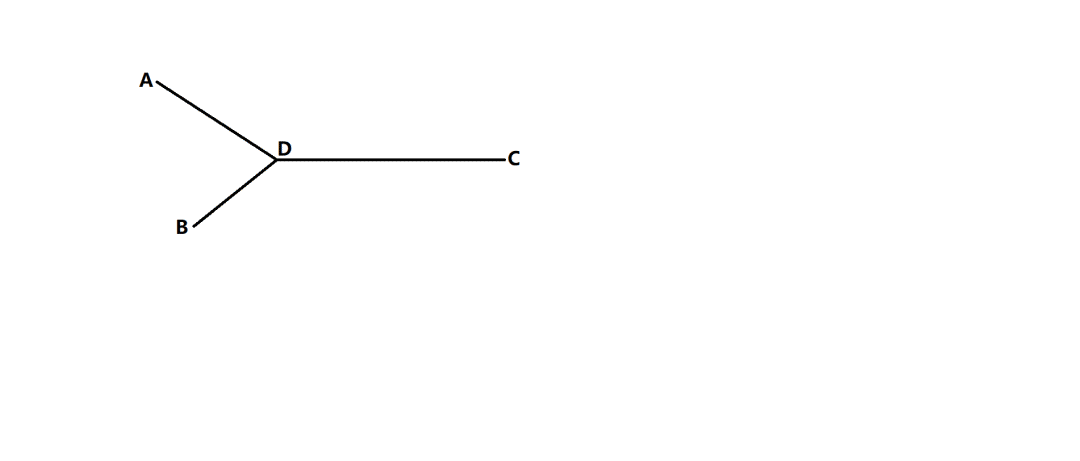每日一课 | 单向链表、双向链表和循环链表图文解析
02.
单向链表、双向链表、循环链表
大家好,我是小C,上期给大家分享—— 数组内存及数组面试常问算法全解析
本期分享内容:单向链表、双向链表和循环链表图文解析
本期小C邀请的是春晨溅雨·4位算法工程师为我们分享《数据结构算法面试全解析》专栏。
数据结构算法面试
单向链表、双向链表和循环链表
链表的种类有很多。我们常常会用到的链表有:单向链表、双向链表和循环链表。
链表不同于数组的地方在于:它的物理存储结构是非连续的,也就是说链表在内存中不是连续的,并且无序。它是通过数据节点的互相指向实现,当前节点除了存储数据,还会存储下一个节点的地址。我们不必在创建时指定链表的长度,因为链表可以无限的插入节点延伸,且插入和删除数据时,其时间复杂度都是 O(1)。
1. 单向链表
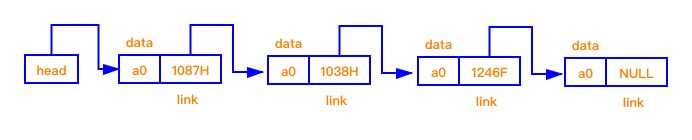
1.1 单向链表结构原理
单向链表在结构上有点向火车,你可以从“车厢 1”走至”车厢 2“,看看“车厢 2”里面都装了什么货品,但是如果你已经在“车厢 2”,想看“车厢 1”里的货品,单向链表是不能做到的,咱们继续看图说明:
1.2 单向链表 Java 实现
上面介绍了单向链表的结构,接下来用 Java 语言实现单向链表,因为这在面试中常常会让你手写一个链表出来,语言不受限制,理解了就能通用了。
首先我们需要先定义一个 Node 类,该对象代表链表中的一个节点。该对象包含了我们上述所说的 data,data 的类型我们定义成范型,这样定义的好处就是我们往该链表结构中存储任意对象,具有通用性。那么如何让这个 Node1 节点可以指向另一个 Node2 节点呢,很简单,在该 Node1 节点中存储下一个 Node2 节点对象。这样我们就可以通过 Node1 节点获取到 Node2 节点,如此嵌套,就形成了我们所要的链表结构。代码如下:
class Node {
//包可见性
Node next;
T data;
/**
* 构造函数
* @auther T-Cool
* @description 构造一个新节点
* 新元素与链表结合节点
*/
public Node(T data) {
this.data = data;
}
@Override
public String toString() {
return data.toString();
}
}
定义完 Node 节点,让我们再定义一个链表类 LinkedList:
public class LinkedList {
class Node {
Node next;
T data;
/**
* 构造函数
* @auther T-Cool
* @description 构造一个新节点
* 新元素与链表结合节点
*/
public Node(T data) {
this.data = data;
}
@Override
public String toString() {
return data.toString();
}
}
private Node head; // 链表表头
private int size; // 链表大小
public LinkedList() {
head = new Node(null);
}
public Node getHead() {
return head;
}
}
上述代码链表类 LinkedList 中定义了两个属性:head 是表头,size 代表链表的大小。
两个方法:构造函数和获取头节点的方法。以上就是一个完整的链表结构。说到数据结构那一定会涉及到对其增删改查。
整体的代码如下,方法功能介绍:
add(E data, int index):向链表中指定位置的元素(0 - size),返回新节点
add(E data):向链表末尾添加元素,返回新节点
add(Node node):向链表尾部添加新节点
remove(int index) :删除链表中指定位置的元素(0 ~ size-1)
removeDuplicateNodes() :删除链表中的重复元素(外循环 + 内循环)
getEndK(int k):找出单链表中倒数第 K 个元素(双指针法,相差 K-1 步)
/**
* @auther T-Cool
* @date 2020/2/12 下午 8:13
* @param
*/
public class LinkedList {
class Node {
//包可见性
Node next;
T data;
/**
* 构造函数
*
* @auther T-Cool
* @description 构造一个新节点
* 新元素与链表结合节点
*/
public Node(T data) {
this.data = data;
}
@Override
public String toString() {
return data.toString();
}
}
private Node head; // 链表表头
private int size; // 链表大小
public LinkedList() {
head = new Node(null);
}
public Node getHead() {
return head;
}
/**
* @description 向链表中指定位置的元素(0 - size),返回新节点
* @param data
* @param index
* @throws Exception
*/
public Node add(E data, int index) throws Exception {
if (index > size) {
throw new Exception("超出范围...");
}
Node cur = head;
for (int i = 0; i < index; i++) {
cur = cur.next;
}
Node node = new Node(data); // 将新元素链入链表
cur.next = node;
size++;
return node;
}
/**
* @description 向链表末尾添加元素,返回新节点
* @param data
* @throws Exception
*/
public Node add(E data) throws Exception {
return add(data, size);
}
/**
* @description 向链表尾部添加新节点
* @param node
*/
public void add(Node node){
Node cur = head;
while(cur.next != null){
cur = cur.next;
}
cur.next = node;
while(node != null){
size ++;
node = node.next;
}
}
/**
* @description 删除链表中指定位置的元素(0 ~ size-1)
* @param index
* @return
* @throws Exception
*/
public E remove(int index) throws Exception {
if (index > size - 1 || index < 0) {
throw new Exception("超出范围...");
}
Node cur = head;
for (int i = 0; i < index; i++) {
cur = cur.next;
}
Node temp = cur.next;
cur.next = temp.next;
temp.next = null;
size--;
return temp.data;
}
/**
* @description 向链表末尾删除元素
* @return
* @throws Exception
*/
public E remove() throws Exception {
return remove(size - 1);
}
/**
* @description 删除链表中的重复元素(外循环 + 内循环)
* 时间复杂度:O(n^2)
*/
public void removeDuplicateNodes() {
Node cur = head.next;
while (cur != null) { // 外循环
Node temp = cur;
while (temp != null && temp.next != null) { // 内循环
if (cur.data.equals(temp.next.data)) {
Node duplicateNode = temp.next;
temp.next = duplicateNode.next;
duplicateNode.next = null;
size --;
}
temp = temp.next;
}
cur = cur.next;
}
}
/**
* @description 找出单链表中倒数第 K 个元素(双指针法,相差 K-1 步)
* @param k
* @return 时间复杂度:O(n)
*/
public Node getEndK(int k) {
Node pre = head.next;
Node post = head.next;
for (int i = 1; i < k; i++) { // pre 先走 k-1 步
if (pre != null) {
pre = pre.next;
}
}
if (pre != null) {
// 当 pre 走到链表末端时,post 正好指向倒数第 K 个节点
while (pre != null && pre.next != null) {
pre = pre.next;
post = post.next;
}
return post;
}
return null;
}
/**
* @description 返回链表的长度
* @return
*/
public int size(){
return size;
}
}
通过上述代码我们就可以实现对单向链表的一些增删改查的操作了。实际上,在 JDK 中已经为我们封装好了,其实现原理和上面的代码大同小异,有兴趣的同学可以看下 LinkedList 的源码。
2019 阿里秋招面试真题:
这道题是笔者在面试大厂时经常遇到的一个经典算法题,实现方法很多,这里介绍一种性能比较优的解法,大家好好听,好好学:
如何判断单链表是否存在环
首先创建两个指针 1 和 2(在 java 里就是两个对象引用),同时指向这个链表的头节点。然后开始一个大循环,在循环体中,让指针 1 每次向下移动一个节点,让指针 2 每次向下移动两个节点,然后比较两个指针指向的节点是否相同。如果相同,则判断出链表有环,如果不同,则继续下一次循环。
public static boolean isLoopList(ListNode head){
ListNode slowPointer, fastPointer;
//使用快慢指针,慢指针每次向前一步,快指针每次两步
slowPointer = fastPointer = head;
while(fastPointer != null && fastPointer.next != null){
slowPointer = slowPointer.next;
fastPointer = fastPointer.next.next;
//两指针相遇则有环
if(slowPointer == fastPointer){
return true;
}
}
return false;
}
如何判断两个单链表是否相交,以及相交点
利用有环链表思路.对于两个没有环的链表相交于一节点,则在这个节点之后的所有结点都是两个链表所共有的。如果它们相交,则最后一个结点一定是共有的,则只需要判断最后一个结点是否相同即可。时间复杂度为 O(len1+len2)。对于相交的第一个结点,则可求出两个链表的长度,然后用长的减去短的得到一个差值 K,然后让长的链表先遍历 K 个结点,然后两个链表再开始比较。
2. 双向链表
通过上面一节,我们知道单向链表不能逆向查找,而双向链表结构的出现正是为了解决该缺点。
2.1 双向链表结构原理
双向链表不同于单向链表的地方在于,单向链表只有后继节点的指针域,而双向链表除了有一个后继节点的指针域外,还有有一个前驱指针域。
模型如下图所示:

顾名思义,前驱指针域存储了当前节点 Node 之前的内存地址,后继节点域存储了后面 Node 的存储地址。
完整双向链表结构如下图:
2.2 双向链表代码实现
根据上一节单向链表的结构我们稍作改动即可实现双向链表的结构,
代码如下:
class Node{
public T val;
public Node next;
public Node pre;
public Node(T val) {
this.val = val;
}
public void displayCurrentNode() {
System.out.print(val + " ");
}
}
与单向链表代码对比不难发现,双向链表在结构上比单向链表多定义了一个 Node 对象,实现了我们在前面所说的前驱指针域的功能。这里的类型依旧用的范型 T,具有通用性。在实际生产开发环境中,你都应该如此定义。displayCurrentNode 方法用来打印当前节点的值,如果这里存储的是对象,则打印当前对象的内存地址。
相比于单向链表,双向链表灵活之处在于可以用 O(1)的时间复杂度读取前驱节点的值,轻松的对其进行增删改查。
isEmpty:判断前驱节点是否为空
addPre:插入前驱节点,通过当前节点获取前驱节点,并赋值
addNext:插入后继节点
addBefore:在链表最前面插入新节点
addAfter:在链表最后面插入新节点
deleteFre:删除当前节点的前驱节点
deleteNext:删除当前节点的后继节点
deleteKey:删除当前节点
displayForward: 打印当前节点的前驱节点值
displayBackward:打印当前节点的后继节点值
同时代码中进行了一些备注,方便大家阅读。完整程序见代码块:
import java.io.IOException;
/**
* @author T-Cool
* @date 2020/2/14 下午 12:11
*/
public class DoublyLinkList{
private Node pre;
private Node next;
//初始化首尾指针
public DoublyLinkList(){
pre = null;
next = null;
}
public boolean isEmpty(){
return pre == null;
}
public void addPre(T value){
Node newNode = new Node(value);
// 如果链表为空
if(isEmpty()){
//last -> newLink
next = newNode;
}else {
// frist.pre -> newLink
pre.pre = newNode;
}
// newLink -> frist
newNode.next = pre;
// frist -> newLink
pre = newNode;
}
public void addNext(T value){
Node newNode = new Node(value);
// 如果链表为空
if(isEmpty()){
// 表头指针直接指向新节点
pre = newNode;
}else {
//last 指向的节点指向新节点
next.next = newNode;
//新节点的前驱指向 last 指针
newNode.pre = next;
}
// last 指向新节点
next = newNode;
}
public boolean addBefore(T key,T value){
Node cur = pre;
if(pre.next.val == key){
addPre(value);
return true;
}else {
while (cur.next.val != key) {
cur = cur.next;
if(cur == null){
return false;
}
}
Node newNode = new Node(value);
newNode.next = cur.next;
cur.next.pre = newNode;
newNode.pre = cur;
cur.next = newNode;
return true;
}
}
public void addAfter(T key,T value)throws RuntimeException{
Node cur = pre;
//经过循环,cur 指针指向指定节点
while(cur.val!=key){
cur = cur.next;
// 找不到该节点
if(cur == null){
throw new RuntimeException("Node is not exists");
}
}
Node newNode = new Node(value);
// 如果当前结点是尾节点
if (cur == next){
// 新节点指向 null
newNode.next = null;
// last 指针指向新节点
next = newNode;
}else {
//新节点 next 指针,指向当前结点的 next
newNode.next = cur.next;
//当前结点的前驱指向新节点
cur.next.pre = newNode;
}
//当前结点的前驱指向当前结点
newNode.pre = cur;
//当前结点的后继指向新节点
cur.next = newNode;
}
public void deleteFre(){
if(pre.next == null){
next = null;
}else {
pre.next.pre = null;
}
pre = pre.next;
}
public void deleteNext(T key){
if(pre.next == null){
pre = null;
}else {
next.pre.next = null;
}
next = next.pre;
}
public void deleteKey(T key)throws RuntimeException{
Node cur = pre;
while(cur.val!= key){
cur = cur.next;
if(cur == null){ //不存在该节点
throw new RuntimeException("Node is not exists");
}
}
// 如果 frist 指向的节点
if(cur == pre){
//frist 指针后移
pre = cur.next;
}else {
//前面节点的后继指向当前节点的后一个节点
cur.pre.next = cur.next;
}
// 如果当前节点是尾节点
if(cur == next){
// 尾节点的前驱前移
next = cur.pre;
}else {
//后面节点的前驱指向当前节点的前一个节点
cur.next.pre = cur.pre;
}
}
public T queryPre(T value)throws IOException,RuntimeException{
Node cur = pre;
if(pre.val == value){
throw new RuntimeException("Not find "+value+"pre");
}
while(cur.next.val!=value){
cur = cur.next;
if(cur.next == null){
throw new RuntimeException(value +"pre is not exeist!");
}
}
return cur.val;
}
public void displayForward(){
Node cur = pre;
while(cur!=null){
cur.displayCurrentNode();
cur = cur.next;
}
System.out.println();
}
public void displayBackward(){
Node cur = next;
while(cur!=null){
cur.displayCurrentNode();
cur = cur.pre;
}
System.out.println();
}
}
3.循环链表
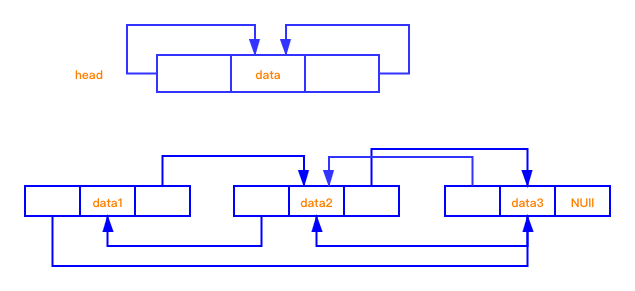
3.1 循环链表结构原理
循环链表相对于单向链表是一种特别的链式存储结构。循环链表与单链表很相似,唯一的改变就是将单链表中最后一个结点和头结点相关联,即将最后一个节点的后继指针域指向了头节点,这样整个链表结构就行成了一个环。这样改造的好处是当我们想要获取链表中的某个值时,表中的任何一个结点都能通过循环的方式到达该节点,并获取到该值。让我们看下模型图,如下:

看完图大家应该很容易循环链表,如果是空的循环链表,当前节点的指针域指向自己。如果是非空循环链表,则将 dataN 的指针域指向 data0。如此,循环链表即已实现。
接下来看下用 Java 如何定义一个循环链表。
public Node(Object data){
this.data = data;
}
}
下面的代码块实现了循环列表的增删改查功能,读者可以直接拿来运行哦~
```Java
/**
* @author T-Cool
* @date 2020/2/14 下午 3:57
*/
public class loopLinkedList {
public int size;
public Node head;
/**
* 添加元素
* @param obj
* @return
*/
public Node add(Object obj){
Node newNode = new Node(obj);
if(size == 0){
head = newNode;
head.next = head;
}else{
Node target = head;
while(target.next!=head){
target = target.next;
}
target.next = newNode;
newNode.next = head;
}
size++;
return newNode;
}
/**
* 在指定位置插入元素
* @return
*/
public Node insert(int index,Object obj){
if(index >= size){
return null;
}
Node newNode = new Node(obj);
if(index == 0){
newNode.next = head;
head = newNode;
}else{
Node target = head;
Node previous = head;
int pos = 0;
while(pos != index){
previous = target;
target = target.next;
pos++;
}
previous.next = newNode;
newNode.next = target;
}
size++;
return newNode;
}
/**
* 删除链表头部元素
* @return
*/
public Node removeHead(){
if(size > 0){
Node node = head;
Node target = head;
while(target.next!=head){
target = target.next;
}
head = head.next;
target.next = head;
size--;
return node;
}else{
return null;
}
}
/**
* 删除指定位置元素
* @return
*/
public Node remove(int index){
if(index >= size){
return null;
}
Node result = head;
if(index == 0){
head = head.next;
}else{
Node target = head;
Node previous = head;
int pos = 0;
while(pos != index){
previous = target;
target = target.next;
pos++;
}
previous.next = target.next;
result = target;
}
size--;
return result;
}
/**
* 删除指定元素
* @return
*/
public Node removeNode(Object obj){
Node target = head;
Node previoust = head;
if(obj.equals(target.data)){
head = head.next;
size--;
}else{
while(target.next!=null){
if(obj.equals(target.next.data)){
previoust = target;
target = target.next;
size--;
break;
}else{
target = target.next;
previoust = previoust.next;
}
}
previoust.next = target.next;
}
return target;
}
/**
* 返回指定元素
* @return
*/
public Node findNode(Object obj){
Node target = head;
while(target.next!=null){
if(obj.equals(target.data)){
return target;
}else{
target = target.next;
}
}
return null;
}
/**
* 输出链表元素
*/
public void show(){
if(size > 0){
Node node = head;
int length = size;
System.out.print("[");
while(length > 0){
if(length == 1){
System.out.print(node.data);
}else{
System.out.print(node.data+",");
}
node = node.next;
length--;
}
System.out.println("]");
}else{
System.out.println("[]");
}
}
}
4. 小试牛刀
4.1 2019 爱奇艺秋招面试真题:删除链表的中间节点
题目:
实现一种算法,删除单向链表中间的某个节点(即不是第一个或最后一个节点),假定你只能访问该节点。
示例:
输入:单向链表 a->b->c->d->e->f 中的节点 c
结果:不返回任何数据,但该链表变为 a->b->d->e->f
解题思路:
直接删除下一个结点。表面删除当前节点,实际删除下一个结点。
代码实现:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public void deleteNode(ListNode node) {
//思路:将下一个结点的值赋给当前节点,当前节点的下一个结点为下下一个结点。
node.val = node.next.val;
node.next = node.next.next;
}
}
4.2 2019 阿里巴巴秋招面试真题:如何找出有环链表的入环点?
解题思路:
假设从链表头节点到入环点的距离是 D,链表的环长是 S。那么循环会进行 S 次(为什么是 S 次,有心的同学可以自己揣摩下),可以简单理解为 O(N)。除了两个指针以外,没有使用任何额外存储空间,所以空间复杂度是 O(1)。
代码实现:
public static ListNode findEntranceInLoopList(ListNode head){
ListNode slowPointer, fastPointer;
//使用快慢指针,慢指针每次向前一步,快指针每次两步
boolean isLoop = false;
slowPointer = fastPointer = head;
while(fastPointer != null && fastPointer.next != null){
slowPointer = slowPointer.next;
fastPointer = fastPointer.next.next;
//两指针相遇则有环
if(slowPointer == fastPointer){
isLoop = true;
break;
}
}
//一个指针从链表头开始,一个从相遇点开始,每次一步,再次相遇的点即是入口节点
if(isLoop){
slowPointer = head;
while(fastPointer != null && fastPointer.next != null){
//两指针相遇的点即是入口节点
if(slowPointer == fastPointer){
return slowPointer;
}
slowPointer = slowPointer.next;
fastPointer = fastPointer.next;
}
}
return null;
}
4.3 美团面试真题 环形单链表约瑟夫问题
题目
输入:一个环形单向链表的头节点 head 和报数 m.
返回:最后生存下来的节点,且这个节点自己组成环形单向链表,其他节点都删除掉。
代码实现:
public static Node josephusKill(Node head, int m) {
if(head == null || m < 1)
return head;
Node last = head;
//定位到最后一个节点
while (head.next != last) {
head = head.next;
}
int count = 0;
while (head.next != head) {
if (++count == m) {
head.next = head.next.next;
count = 0;
} else {
head = head.next;
}
}
return head;
}
4.4 2019 饿了么秋招面试真题:链表相交
题目:
给定两个(单向)链表,判定它们是否相交并返回交点。请注意相交的定义基于节点的引用,而不是基于节点的值。换句话说,如果一个链表的第 k 个节点与另一个链表的第 j 个节点是同一节点(引用完全相同),则这两个链表相交。
示例 1:
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Reference of the node with value = 8
输入解释:相交节点的值为 8 (注意,如果两个列表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
解题思路:
根据题意,两个链表相交的点是指: 两个指针指向的内容相同,则说明该结点记在 A 链表上又在 B 链表上,进而说明 A 和 B 是相交的
而对于相交的情况,两条链表一定是这种结构:
代码实现:
class Solution {
public:
ListNode *getInterpNode(ListNode *headA, ListNode *headB) {
ListNode *t1 = headA; ListNode *t2 = headB;
while(t1 != t2){
if (t1 == NULL)
t1 = headB;
else t1 = t1->next;
if (t2 == NULL)
t2 = headA;
else t2 = t2->next;
}
return t1;
}
};
今日内容有get吗,欢迎各位留言讨论!
下期预告:如何用双向链表实现LRU淘汰机制算法
以上专栏均来自CSDN GitChat专栏《数据结构算法面试全解析》,作者春晨溅雨·4位算法工程师,专栏详情可识别下方二维码查看哦!
了解更多详情
可识别下方二维码