存储(五)—— B+树
如果你去应聘后台开发的职位,面试一圈下来,多半会发现,都在说mysql,都在说innodb,都在说索引,都在说B+树,B+树究竟是何物,看完此篇,如果说会让你在面试中游刃有余,我并不开心,如果说会让你对B+树产生的缘由以及背后的思想有所了解,那么我将倍感欣慰,如果能让你由此产生更多疑问和思考,我将手舞足蹈。
为什么要有B+树
B+树是对B树的改进,B树是对红黑树的改进,红黑树是对二三树的改进,二三树是对平衡树的改进,平衡树是对二叉树的改进,所以,先来看看:
为什么要有二叉树
不考虑hash表(不支持范围查找)的情况下,有什么数据结构可以做到尽可能快的查找和插入元素呢?
我们先来看最基本的两种数据结构:数组和链表。
假设我们有这样一个数字序列需要存储:1,3,6,2,4,5。
无脑存,来一个存一个,这样可以保证元素插入的时间复杂度是O(1),最后数组和链表是这个样子的:
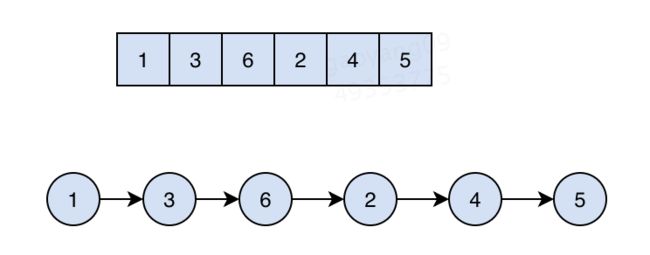
然后如果从这样的数组和链表中查找某个元素,那除了遍历,别无他法了,所以查找的时间复杂度是O(n),且不说范围查找的事情,单是这个O(n)是无论如何也无法接受的。
所以,我们得做点什么,让查询更快一些,按照我们翻书(比如让你翻开书的第几页)的常识,二分查找是很快的(O(logn)),但二分查找的前提是,所有的元素是排好序的。所以我们不能再无脑存了,必须保证每次插入元素后,数组或者链表都是有序的。
但是但是,问题又来了,对于数组来说,插入元素时,需要把后面的元素挨个后移,也就是说,插入元素的时间复杂度是O(n)。
链表呢?链表插入时不需要移动元素,但是链表这种数据无法进行二分查找的!
那有没有办法把数组和链表的优点结合一下,保证插入时不需要移动那么多元素,查找时还可以用二分呢?
于是,排序二叉树出现了:
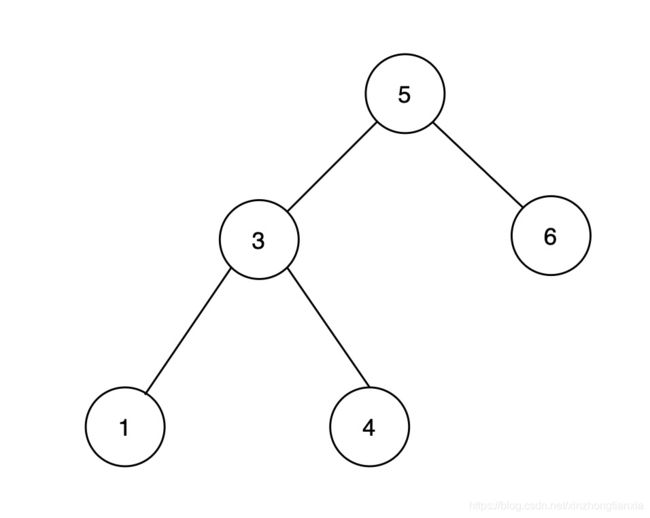
这种结构,综合了数组和链表的优点,每个节点左边的元素都比它小,右边的节点都比它大,这样无论是插入还是查找某个元素,平均时间复杂度都是O(logn),简直完美?
为什么要有平衡二叉树
不是的,之所以说平均时间复杂度是O(logn),那就说明有不平均的时候,考虑最坏的情况,比如插入元素的顺序是1,2,3,4,5,6,那么,最后得到的“二叉树”是这个样子的:
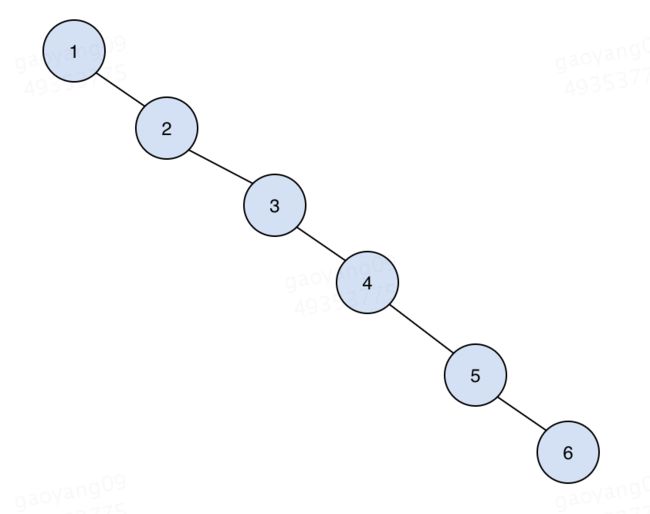
在这样的一棵二叉树中查找元素的时间复杂度显然是O(n),所以我们得想办法避免这种情况,使得这棵树无论如何尽可能在插入元素后仍然保持“平衡”。只有平衡才能保证二分查找的每一步过滤掉尽可能多的元素。
拿1,2,3这三个元素举例,插入时可以通过一些额外的旋转操作来保证二叉树的平衡,示意图如下:
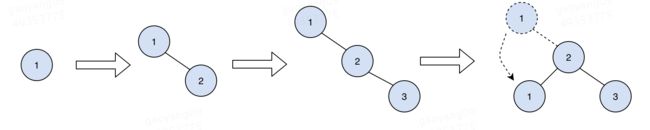
具体旋转算法比较复杂,本人不擅长,这里就不做介绍了,有兴趣可以网上搜一下,有很多不错的文章。
到目前为止,平衡二叉树看起来很完美,那
为什么要有二三树
因为AVL树(平衡二叉树)是一种完全平衡的二叉树,为了在插入和删除节点时维护这种完美的平衡性,其翻转操作在某些情况下代价很大(需要一直翻转到根节点),所以,如果我们可以牺牲一点点查询的性能(当然,整体时间复杂度仍然保证是对数级别的),来减小插入和删除节点时为了保持平衡而带来的代价,还是很不错的。
怎么做才能保证调整树的平衡时所用的步骤少一些呢?这就需要把二叉树变一下,是的一个节点最多可以容纳两个值,一个变形后的二叉树(又叫做二三树)大概是这个样子的:

原则上仍然保证每个节点的左边节点的值都比自己小,右边都比自己大,如果某个阶段中有两个值,那么这两个值中间的元素们都位于中间子树下面(比如上图中的H)。
插入节点时,总是插入到已经存在的节点中,如果插入后节点中的元素个数大于2,那么该节点就会进行分裂,多出来的元素向上级节点融合。
因为二三树的特点,可以保证每次插入和删除节点时,只需要局部调整即可保证整棵树的平衡,所以其插入和删除的效率理论上要比平衡二叉树好一些。但是,因为插入、删除节点的过程中,会遇到多种不同的节点(包含一个元素的节点、两个元素的节点、三个元素的临时节点),因此代码实现上极其复杂,所以,前辈们想了其他的办法,把二三树又变形了一下,在保证其调整平衡时所需步骤少的优点的同时,在代码实现上也"清晰了"不少,这个变形后的二三树就是红黑树了。
大名鼎鼎的红黑树
我想,凡是计算机专业的学生或者从事计算机相关工作的同学应该都对红黑树这个名字很熟悉,先来看看红黑树长什么样子:
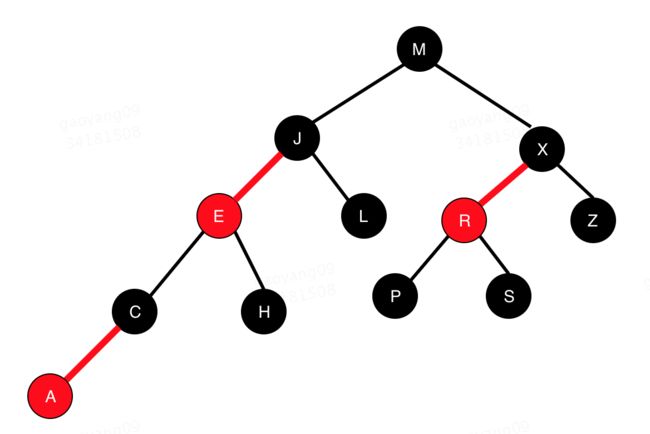
关于红黑树定义、诸多特点以及具体实现不是本文的重点,网上很多文章以及各大算法书都讲的很清楚,大家有兴趣可以去看看。
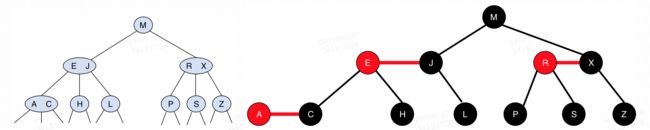
这里只说一点:让我们试着把红色节点拉平之后和之前的二三树放到一起看看,就知道红黑树和二三树的关系了:
B树
说了这么多,和索引有啥关系?和B+树有啥关系?为啥索引不直接设计成红黑树的结构?
红黑树在内存中运行,是没问题的,Java中的TreeMap以及HashMap中都有红黑树的实现。
但是,如果数据量很大(mysql表动辄上千万数据),大到内存装不下了呢?这时就要把数据存放到磁盘上,我们已经知道,磁盘上的随机查找速度很慢,如果二叉树的高度有十几层,那么查找一条位于叶子节点的数据需要转动磁盘十几次,这种数据查询效率显然是不能接受的。
我们注意到,磁盘io的次数和树的高度有关系 --> 树的高度和节点的总数有关系 --> 节点的总数和数据量的大小有关系。
现在我们既想减少磁盘io的次数,又不能减少数据量,看起来是无解的。
回过头来再看看上面的二三树,看看有没有什么启发?
二三树允许一个节点存储两个元素,如果我们继续扩展,允许一个几点存储的元素再多一些,比如几千条,那么我们树的节点的数量也将减少几千倍,树的高度自然低了,一次查找磁盘io的次数也就少了。
联想到我们在第三篇**《缓存和局部性原理》**中提到的,磁盘实际读取时,会进行预读,一次读取一个磁盘块大小(记得Linux是4K)的数据到内存中,所以我们一个节点的大小设计为一次磁盘预读数据量的大小就刚刚好了。
这样一来,我们设想中的数就变成下面这个样子了:
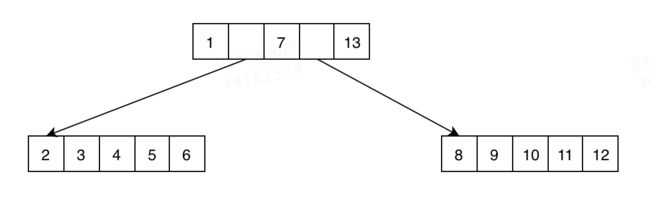
每个节点中都存了数据以及指向下一层节点的指针,比如我们想要查找3这个元素,查找步骤大致是下面这个样子的:
- 读取根节点到内存,根据指针找到3所在的节点
- 读取3所在的节点到内存
- 在读到内存的数据中(2、3、4、5、6)找到3
也许有同学会有疑问,节点中存放的数据太多的情况下,在一个节点中查找某个元素会不会很慢。答案是不会,此时节点的数据已经在内存中了,而且数据是有序的,我们可以用类似二分查找的算法来吧时间复杂度控制在O(lgn)。内存中的运算还是很快的。
上图中的结构,就是B树了。
B+树
B树这种结构在实际运用中还有没有什么需要改进的地方呢?
这里比较容易想到的有两点:
- 我们总是希望能尽快的定位到数据所在的节点,这样一来,我们就希望一次读取的节点中尽可能包含更多的信息,那么我们其实可以在叶子节点之外的其他层节点中只存放索引字段,而不是存放整条数据,这样一来,节点中存放的信息量大大增加了。
- 我们在实际查找中,经常遇到范围查找,比如这种sql
select * from tableA where id > 15 and id < 100;
对于这种范围查找,B树只能一次次的查找范围内的节点,这实在是不怎么高效。如果我们改进一下,在1的基础上,把所有的叶子节点(叶子节点中真正存储完整的数据)用指针连起来,每个叶子节点都有一个指向前面叶子节点和后面叶子节点的指针,这样一来,范围查询,只需要找到最前面的叶子节点,然后顺着指针,一路找到范围中最后的一个节点就可以了。
经过这两种改造,我们的B+树就诞生了:

其实这里可以再优化一点,我们可以把根节点一直保存在内存中,这样每次查找就都能节省一次I/O了。
按照B+树的这种设计理念,通常我们mysql表索引树的高度不会超过4层(4层可以存储上T的数据了)。
好了,理解了B+树的来龙去脉,我们回过头来看看一些常见的(但是很少人告诉我们为什么要这样做)数据库使用经验:
- 我们平时也会遇到需要分表的时候,前辈们通常会告诉你一个经验值:表中数据超过两千万(or三千万,or五千万)的时候,就需要分表了。
想想这是为啥?这个数量级分表应该就是为了防止B+树的高度从三层增加到四层。 - 也有人会这么告诉你,建立索引的字段最好不要过大。
这又是为啥?你想啊,B+树的一个节点的大小是固定的,用int型的字段建立索引和用long型的字段建立索引,想想树的高度会不会有差距? - 为啥索引有最左前缀匹配原则?
- 多列组合索引的存储是什么样子的?
- 。。。
诸多问题都是围绕着B+树的结构特点来的,融汇贯通之后,便不是什么难事了。
B+树的改进
在过去以及未来很长的一段时间内,B+树已经而且应该将会仍然作为使用最广泛的索引结构而存在。
但是,当今数据量暴增的时代,mysql这种传统的数据库也会有其局限的地方,主要体现在两点:
- 数据采集场景,数据量巨大,数据需要以极高的吞吐量源源不断的写入,这种场景下,B+树的结构就力不从心了,毕竟B+树每次写入数据前,先要查找数据应该写入的位置,虽然其查找速度很快,但是在大数据量的场景下,已经不太够用了。
- 当你发现现在的数据库表已经足够大了,需要重新分表甚至分库时,噩梦就来了(操作过的都知道有多麻烦)。
为了解决这些问题,一种新的存储结构出现了,且看下一篇:
《存储(六)———— LSM Tree》