分治算法课后习题

---

引言

在分治算法——经典案例分析这篇博客中，我们从二分搜索这个案例入手，介绍了分治算法的三个步骤：分解、解决、合并，并且留下了几道课后习题。本文可作为前面这篇文章课后习题的参考答案，如果你的解题思路和恭仔是类似的，那恭喜你已经掌握了分治这一解题利器。

题一：寻找中位数

输入: 数组a[1…n]
输出: a[1],…,a[n]的中位数

对于中位数问题，我们可以将其转变为找到第k小的数。

输入: 数组a[1…n]，整数k
输出: a中第k小的数

二分排序

对于上述思路，可以先对数组进行二分排序：
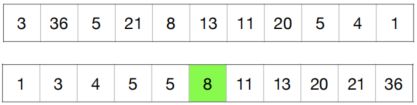
划分: 选择一个主元V，然后重新排列数组。

• L: 小于v的元素; M: 等于v的元素; R: 大于v的元素

1. k =4: 第4小的数必然是 5 (3 < k< 3 +2)

2. k =1: 第1小的数必然在L中，且必然是L中第1小的数 (k<3)

3. k =8: 第8小的数必然在R中，且必然是R中第3小的数 (k >3 + 2)
   ​
   $$select(a,k)=\{\begin{array}{cc}select(L,K)& k\le \left|L\right|\\ v& \left|L\right|\le k\le \left|L\right|+\left|M\right|\\ select(R,k-\left|L\right|-\left|M\right|)& k>\left|L\right|+\left|M\right|\end{array}$$

int partition(vector<int>& arr, int low, int high) {
    int pivot = arr[high]; // 选取最后一个元素作为基准值
    int i = low - 1; // 小于基准值的部分的右边界

    for (int j = low; j < high; j++) {
        if (arr[j] < pivot) {
            i++;
            swap(arr[i], arr[j]); // 将较小元素移到左边
        }
    }

    swap(arr[i + 1], arr[high]); // 将基准值放置在正确的位置
    return i + 1; // 返回基准值的位置
}

void quickSort(vector<int>& arr, int low, int high) {
    if (low < high) {
        int pi = partition(arr, low, high);

        quickSort(arr, low, pi - 1); // 递归地对左半部分排序
        quickSort(arr, pi + 1, high); // 递归地对右半部分排序
    }
}

double findMedian(vector<int>& arr) {
    int n = arr.size();
    quickSort(arr, 0, n - 1);

    if (n % 2 == 1) {
        return arr[n / 2];
    } else {
        return (arr[n / 2 - 1] + arr[n / 2]) / 2.0;
    }
}

int main() {
    vector<int> arr = {6, 2, 8, 1, 4, 7, 3, 5};

    double median = findMedian(arr);
    cout << "数组的中位数是：" << median << endl;
    return 0;
}

Mom-select

对于二分排序

1. 如果能够选择一个主元v，使得|L|=|R|，那么 $$T\left(n\right)=T\left(\frac{n}{2}\right)+n\Rightarrow T\left(n\right)=O\left(n\right)$$
2. 随机选择一个元素作为主元

• 最好情况: O(n)
• 最坏情况: $$T\left(n\right)=T\left(n-1\right)+n\Rightarrow T\left(n\right)=O\left(n^2\right)$$
• 平均情况: O(n)

有没有别的方法来选择主元V，使得最坏情况下O(n)呢?

有的，关键是找到⼀个合适的主元V使得数组二分得更加均匀，Mom-Select（Median of Medians）是一种用于在无序数组中找到第k小元素的选择算法。它的基本思想是通过分治和选择的方法来快速找到第k小的元素。

Mom-select步骤：

1. 分组：将数组分成大小为m（通常取5）的子组（除了最后一组可能小于m）。
2. 找到各组的中位数：对于每个子组，使用任何方法（如插入排序）找到其中位数。
3. 找到中位数的中位数：使用Mom-Select算法递归地找到所有中位数的中位数，记作p。
4. 划分：使用p作为枢纽元素对数组进行划分，将小于p的元素放在左侧，大于p的元素放在右侧，同时得到p所在的位置q。
5. 递归：如果q=k，则已找到第k小的元素，返回p。否则，根据q和k的大小关系，在左侧或右侧的子数组中继续递归查找。

// 在较小规模的数组中使用插入排序
void insertionSort(vector<int>& arr, int left, int right) {
    for (int i = left + 1; i <= right; i++) {
        int key = arr[i];
        int j = i - 1;
        while (j >= left && arr[j] > key) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
}

// 找到数组的中位数
int findMedian(vector<int>& arr, int left, int right) {
    insertionSort(arr, left, right);
    return left + (right - left) / 2;
}

// 交换元素位置
void swap(vector<int>& arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

int partition(vector<int>& arr, int left, int right, int pivotIndex) {
    int pivotValue = arr[pivotIndex];
    swap(arr, pivotIndex, right);  // 将枢纽元素移到右边
    int i = left;

    for (int j = left; j < right; j++) {
        if (arr[j] < pivotValue) {
            swap(arr, i, j);
            i++;
        }
    }

    swap(arr, i, right); // 将枢纽元素移到正确的位置
    return i;
}

int momSelect(vector<int>& arr, int left, int right, int k) {
    if (left == right) {
        return arr[left];
    }

    int n = right - left + 1;
    int i;
    vector<int> medians((n + 4) / 5);

    for (i = 0; i < n / 5; i++) {
        medians[i] = findMedian(arr, left + i * 5, left + i * 5 + 4);
    }

    if (i * 5 < n) {
        medians[i] = findMedian(arr, left + i * 5, left + i * 5 + n % 5 - 1);
        i++;
    }

    int medianOfMedians = (i == 1) ? medians[i - 1] : momSelect(medians, 0, i - 1, i / 2);

    int pivotIndex = partition(arr, left, right, medianOfMedians);
    int rank = pivotIndex - left + 1;

    if (k == rank) {
        return arr[pivotIndex];
    } else if (k < rank) {
        return momSelect(arr, left, pivotIndex - 1, k);
    } else {
        return momSelect(arr, pivotIndex + 1, right, k - rank);
    }
}

---

题二：逆序对

在一个数组A[1…n]中，逆序对 (inversion) 是一对索引(i,j)，满足iA[j]。一个包含n个元素的数组中的逆序对数量介于0(如果数组已排序)和2n(如果数组完全逆序)之间。设计一个高效的算法计算数组A[1…n]中逆序对的数量。

基本二分递归求解思路:

1. 将数组分成两半，并递归地计算左半部分和右半部分的逆序对数量。
2. 统计左半部分、右半部分以及跨越两个部分的逆序对数量。
3. 将两个部分合并，并在合并的过程中将逆序对数量更新。

//merge 合并两个有序数组并统计逆序对数量
int merge(vector<int>& arr, int left, int mid, int right) {
    int inversions = 0;
    int n1 = mid - left + 1;
    int n2 = right - mid;

    // 创建临时数组来存储左右两部分
    vector<int> leftArray(n1);
    vector<int> rightArray(n2);

    for (int i = 0; i < n1; i++)
        leftArray[i] = arr[left + i];
    for (int i = 0; i < n2; i++)
        rightArray[i] = arr[mid + 1 + i];

    int i = 0, j = 0, k = left;

    while (i < n1 && j < n2) {
        if (leftArray[i] <= rightArray[j]) {
            arr[k++] = leftArray[i++];
        } else {
            arr[k++] = rightArray[j++];
            inversions += (n1 - i);
        }
    }

    while (i < n1) {
        arr[k++] = leftArray[i++];
    }

    while (j < n2) {
        arr[k++] = rightArray[j++];
    }

    return inversions;
}

//递归地计算逆序对数量
int countInversionsHelper(vector<int>& arr, int left, int right) {
    int inversions = 0;

    if (left < right) {
        int mid = left + (right - left) / 2;
        inversions += countInversionsHelper(arr, left, mid);
        inversions += countInversionsHelper(arr, mid + 1, right);
        inversions += merge(arr, left, mid, right);
    }

    return inversions;
}

时间复杂度分析

1. 归并排序的时间复杂度：
   - 分解阶段：将数组递归地分解成越来越小的子数组，需要 log n 层，每层的时间复杂度是 O(n)。
   - 合并阶段：每层合并的时间复杂度也是 O(n)。
   因此，归并排序的总时间复杂度是 O(n log n)。
2. 合并操作中统计逆序对数量的时间复杂度：
   - 在合并两个有序数组的过程中，每当将一个元素从右侧数组移到左侧数组，就发现了一个逆序对。由于合并操作的总次数不超过 n，因此统计逆序对的时间复杂度是 O(n)。

综合以上两点，基于归并排序的逆序对算法的总时间复杂度是 O(n log n)。

---

题三：支配点

给定二维平面上两个不同的点p和q，如果p.x < q.x且p.y < q.y，称q支配p。给定一个点集P，设计一个高效的算法，计算每一个点p∈P支配的点的数量。给出算法的基本思路和伪代码描述，分析算法的时间复杂度。

二分法求解思路：

1. 分解：将点集 P 平均分成两部分，分别处理左半部分和右半部分。
2. 解决：递归地计算左半部分和右半部分中每个点支配的点的数量。
3. 合并：将左半部分和右半部分的结果合并起来，得到整个点集 P 中每个点支配的点的数量。

function countDominations(points):
    if points.length == 1:
        return 0
    
    // 分解
    mid = points.length / 2
    leftPoints = points[0...mid]
    rightPoints = points[mid+1...end]
    
    // 解决子问题
    leftDominations = countDominations(leftPoints)
    rightDominations = countDominations(rightPoints)
    
    // 合并结果
    dominations = leftDominations + rightDominations
    
    // 统计左边支配右边的情况
    for each point in leftPoints:
        for each point in rightPoints:
            if rightPoint.x > leftPoint.x and rightPoint.y > leftPoint.y:
                dominations++
    
    return dominations

时间复杂度分析

1. 分解阶段：将点集 P 平均分成两部分的过程需要 O(n) 的时间。
2. 解决子问题阶段：对左半部分和右半部分分别进行递归处理，需要的总时间是 2*T(n/2)。
3. 合并阶段：合并左半部分和右半部分的结果，需要 O(n) 的时间。
4. 统计左边支配右边的情况：对于每一个左边的点，需要遍历右边的所有点，所以这个过程的复杂度是 O(n^2)。
   T(n) = 2T(n/2) + O(n^2)
   时间复杂度为: O（n^2 log n）

简单地使用分治法求解这个问题的时间复杂度是相当高的，如果点集 P 非常大，需要考虑更优化的算法来提高效率。
通过分析可以发现，复杂度主要来源于第四步：统计点集左边支配右边的情况。这一步由于点是混乱划分的所以无法进行高效比较。

优化措施：先对点按照 x 坐标进行排序

1. 首先，对点集P按x值进行排序。
2. 从x值最大的点开始，向左遍历。这个点（由于是x值最大的）支配其左侧所有y值较小的点。
3. 对于每个后续的点，我们可以在其右侧已经处理过的点中搜索y值大于当前点的点，并计算它们的数量。
4. 每次处理一个点后，我们可以将其添加到一个已处理的点的列表中，并保持此列表按y值排序，以便进行后续的搜索。

function count_dominating_points(P):
    sort(P, key=lambda p: p.x)
    
    processed = []  # 已处理的点，按y值排序
    results = []
    
    for i in range(len(P) - 1, -1, -1):  # 从右到左遍历
        p = P[i]
        
        # 在processed中找到y值大于p.y的点的数量
        count = sum(1 for q in processed if q.y > p.y)
        
        results.append(count)
        
        # 将p插入processed，并保持按y值排序
        insert_sorted_by_y(processed, p)
    
    return reversed(results)

function insert_sorted_by_y(processed, p):
    index = find_insert_index(processed, p.y)
    processed.insert(index, p)

function find_insert_index(processed, y):
    for i in range(len(processed)):
        if processed[i].y > y:
            return i
    return len(processed)

这种方法的时间复杂度在最坏情况下是O($n^2$)。这是因为对于每个点，我们可能需要在processed中搜索其所有先前的点。不过，由于我们正在利用排序来简化搜索，实际运行时间可能会更快，特别是对于那些有明显支配关系的点集。

最好的情况是当所有的点按y值也是有序的。在这种情况下，每次插入一个新的点到processed列表都是O(1)操作，因为新点的y值总是小于或等于已处理点的y值。此外，对于每个点，我们不需要检查整个processed列表来确定它支配的点的数量，因为一旦我们遇到一个y值小于或等于当前点的y值的点，我们就知道其后面的所有点的y值也会小于或等于当前点的y值。所以，最好的情况下，对于每个点，计算支配的点的数量也只需要O(1)时间。这意味着总的时间复杂度为O(n)。

具体的运行时间可能会因点的实际分布和其他因素而有所不同。如果点的分布有某种特定的模式，那么实际的运行时间可能会更接近O(n)或介于O(n)和O($n^2$)之间。但在一般情况下，预计复杂度接近O($n^2$)。