PFL-MoE:基于混合专家的个性联邦学习
文章链接:PFL-MoE: Personalized Federated Learning Based on Mixture of Experts
发表会议:APWeb-WAIM 2021(CCF-C)
目录
- 1.背景介绍
-
- 联邦学习
- non-IID
- PFL
- 2.内容摘要
-
- 关键技术
-
- A.PFL-MoE
- B.PFL-MF
- C.PFL-MFE
- 实验结果
- 3.文章总结
1.背景介绍
过去几年,深度学习在AI应用领域(CV、NLP、RS)中快速发展,这离不开海量数据集的支持。这些数据集通常是来自不同组织、设备或用户的数据集合。
分布式机器学习(distributed machine learning, DML)则可以利用大量的工作节点协同进行训练,目前已广泛应用于在大容量数据集上训练大规模的神经网络模型。
然而在许多场景中,数据实际上分布在不同的客户端(属于不同的用户),对隐私很敏感,意味着这些数据无法进行共享。此外,随着边缘设备的存储和计算能力的增长,直接在边缘设备上执行学习越来越受青睐。联邦学习(Federated Learning ,FL)的出现很好的适应了这种场景。
联邦学习
第一个FL系统是由谷歌[1,2]开发的,该系统选择了一个可用的智能手机样本,基于边缘服务器架构更新语言预测模型,取得了很好的效果。
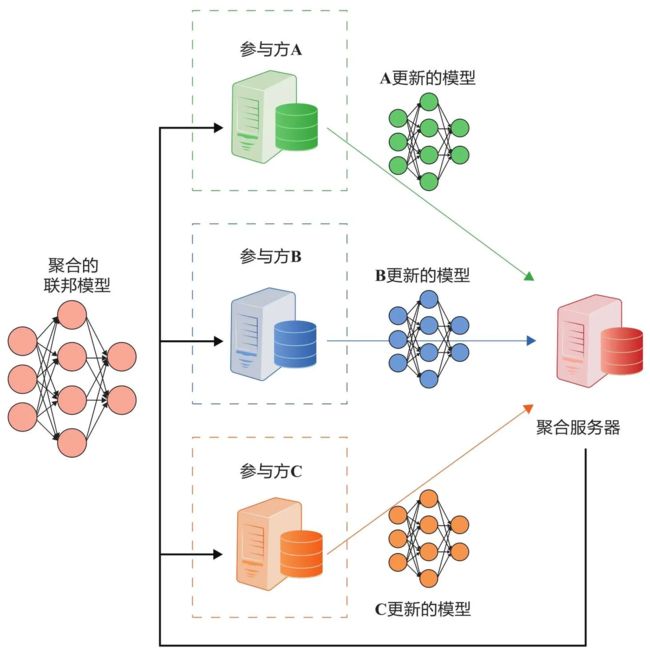
FL允许大量的客户端(移动电话和IoT设备)一起学习一个全局模型,而不需要数据共享。全局模型是通过迭代平均来自小客户端的模型更新而创建的。每轮FL大致包括三个基本阶段:
- FL服务器向每个参与客户端提供全局模型;
- 客户端根据其私有数据进行训练,并将更新后的模型返回服务器;
- FL服务器通过聚合上传的模型获取最新的全局模型。当训练收敛时,最终的全局模型可以获得与通过池化和共享数据训练的模型相似的性能。
联邦学习目前仍然存在许多挑战,包括隐私问题、通信成本、系统异质性和统计异质性:
- 隐私问题:虽然联邦学习只用模型参数进行通信,但研究表明,监视模型更新可以反向派生数据,使得隐私保护成为一个重要问题。关于隐私泄露的风险和保护方法已经发表了大量的文献。
- 通信成本:FL服务器协调参与者进行全局模型的迭代训练,其中上传和下载模型参数需要大量的通信开销。
- 系统异质性:在联邦设置中,所有边缘设备都可以是客户机。在大多数情况下,这些设备的网络资源较少,不能一直保持在线。
- 统计异质性:每个客户端的软硬件资源和计算能力相差很大。
这些问题需要联合学习框架来有效地协调和分配客户端。
non-IID
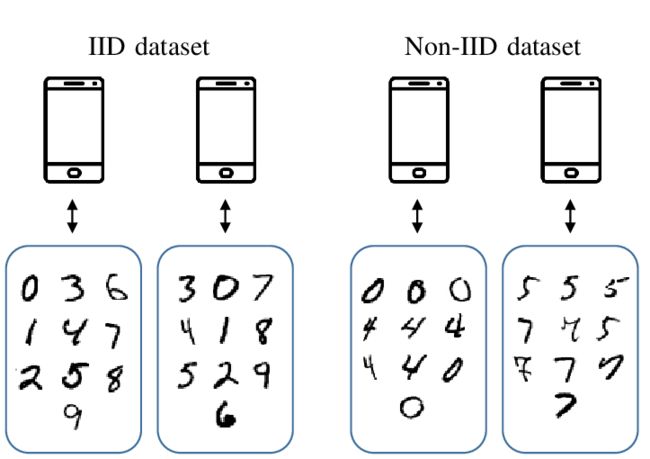
不同客户拥有的数据在统计上具有多样性。数据在客户端之间的分布是自然的不一致性和non-IID (IID,Independent and Identically Distributed),而且数据量也有很大的偏差。由于non-IID数据会导致模型参数波动较大,延迟甚至破坏收敛性,因此non-IID特征对训练的全局模型的收敛性有很大的影响。
如果考虑隐私保护机制,例如差异隐私,情况会更糟。在相同的全局模型下,不同的客户有很大的准确率差异。在一些客户中,全局模型甚至比本地训练的模型更糟糕。人们需要在模型的泛化性和异质性之间做出一定取舍。
大量实验论证了non-IID对于FL的训练影响,与此同时也有一批non-IID数据构造方法和non-IID数据集不断涌现。
- Li等人首次证明了广泛应用于联邦学习的FedAvg在
non-IID数据分布下的收敛性。 - Zhao等人提出了一种共享部分全局数据的方法,以缓解客户端之间的数据差异,从而提高全局模型的收敛速度和性能。
- 在FedProx中,将近端项添加到每个客户端的优化目标中,以限制其更新的漂移,使算法比FedAvg具有更好的鲁棒性和收敛稳定性。
- 个性化联邦学习则是从客户参与联邦学习的动机出发,以提高
non-IID数据分布客户个性化模型的准确性为目标,有效地提高了整体性能。
PFL
在个性化联邦学习(personalized federated learning, PFL)中,每个客户机学习适合自己的数据分发的个性化模型,这比单个全局模型更灵活。为了使联邦全局模型适应于单个客户端,常用的技巧包括微调、多任务学习、知识蒸馏和混合模型。
这些PFL技巧可以有效地改善单个参与者的模型性能,可以做到几乎所有的个性化模型都优于相应的本地训练模型。但个性化总是伴随着泛化性的丢失,具体表现为个性化模型泛化误差的增大。由于客户端只有少量数据,对应的个性化模型可能会与本地数据过度匹配。
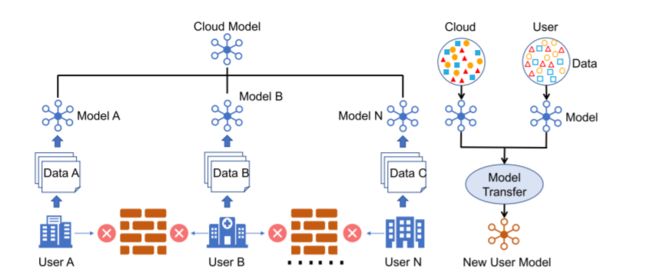
为了解决这个问题,有学者提出了FL+MoE相结合推理范式,具体来说结合了两种模型:在FL+MoE中,所有的客户合作建立一个通用的全局模型,但是维护私有的、适应领域的专家模型。在每个客户端中,全局模型和私有模型分别被视为全局专家和领域专家,它们的输出被Gating Net混合。两种模型的预测比单一全局模型的预测准确得多。
2.内容摘要
受FL+MoE的启发,本文提出了一种个性化的联邦学习方法PFL-MoE,该方法将个性化的模型视为本地专家,并通过MoE模型体系结构将其与联邦全局模型相结合。PFL- MoE是一种通用的方法,可以用现有的PFL算法来实例化。
特别地,本文提出了PFL- MF算法,这是一个基于冷冻(freeze-based,FB)算法的实例。PFL-FB是一种将联邦全局模型应用于单个客户端的有效算法。此外,为了提高门控网络的决策能力,本文对PFL-MF模型结构进行了改进,提出了一种扩展算法PFL-MFE。在各种non-IID的实验设置中,所提算法的全局精度更高,而局部测试精度与PFL-FB相同甚至更好。
关键技术
A.PFL-MoE
PFL-MoE可以分为三个阶段:
- 联邦学习(FL)阶段:遵循传统的FL框架,每个客户参与FL训练。
参数定义:训练客户数量 N;全局模型结构 M G M_{G} MG;全局模型参数 θ ( d 1 ) 维 \theta (d_{1})维 θ(d1)维
其中 θ ∈ R d 1 \theta \in \mathbb{R}^{d_{1}} θ∈Rd1 and R d 1 ∈ R \mathbb{R}^{d_{1}} \in \mathbb{R} Rd1∈R
FL的学习目标为:
min θ ∈ R d 1 F ( θ ) = 1 N ∑ i = 1 N f i ( θ ) \min_{\theta \in \mathbb{R}^{d_{1}}} F(\theta) =\frac{1}{N} \sum_{i=1}^{N} f_{i}(\theta) θ∈Rd1minF(θ)=N1i=1∑Nfi(θ)
对于每一个 f i f_{i} fi,由于数据分布不同,假设第 i i i 个客户的数据分布定义为 D i \mathcal{D} _{i} Di 则:
f i ( θ ) = E ( x , y ) ∼ D i [ L i ( M G ( θ ; x ) , y ) ] f_{i}(\theta)=\mathbb{E}_{(x,y)\sim\mathcal{D}_{i}} [L_{i}(M_{G}(\theta;x),y)] fi(θ)=E(x,y)∼Di[Li(MG(θ;x),y)]
其中 L i ( ⋅ ) L_{i}(·) Li(⋅)是客户 i i i 的损失函数
- 个性化( Personalization) 阶段:每个客户端从FL服务器下载最新的全局模型,然后进行本地适应,以获得基于全局模型和本地数据的个性化模型。
本文选择了基于微调的局部自适应PFL算法
PFL- FT来形式化地描述个性化阶段的细节。具体目标是为每个客户端找到一个好的模型参数,定义 F : R d 1 → R F:\mathbb{R}^{d_{1}} \rightarrow \mathbb{R} F:Rd1→R为全局损耗:
min θ 1 , θ 2 , . . . . , θ N ∈ R d 1 F ( θ 1 , θ 2 , . . . . , θ N ) = 1 N ∑ i = 1 N f i ( θ i ) \min_{\theta_{1},\theta_{2},....,\theta_{N} \in \mathbb{R}^{d_{1}}} F(\theta_{1},\theta_{2},....,\theta_{N}) =\frac{1}{N} \sum_{i=1}^{N} f_{i}(\theta_{i}) θ1,θ2,....,θN∈Rd1minF(θ1,θ2,....,θN)=N1i=1∑Nfi(θi)
f i ( θ i ) = E ( x , y ) ∼ D i [ L i ( y ^ , y ) ] f_{i}(\theta_{i})=\mathbb{E}_{(x,y)\sim\mathcal{D}_{i}} [L_{i}(\hat{y} ,y)] fi(θi)=E(x,y)∼Di[Li(y^,y)]
y ^ = M G ( θ i ; x ) \hat{y}=M_{G}(\theta_{i};x) y^=MG(θi;x)
其中 y ^ \hat{y} y^ 是对应于x的输出伪标签。在PFL-FT中, θ i \theta_{i} θi的初值为全局模型参数,由学习率较小的随机梯度下降法(SGD)更新:
θ i = θ i − α ⋅ ▽ f i ( θ i ) \theta_{i}=\theta_{i}-\alpha·\bigtriangledown f_{i}(\theta_{i}) θi=θi−α⋅▽fi(θi)
- 混合(Mixing)阶段:通过前两个阶段,客户得到两个模型,一个是个性化模型,另一个是全局模型。在混合专家模型结构的基础上,对门控网络的参数进行训练,使模型结合在一起工作。
混合结果
y ~ = ∑ i = 1 n G ( x ) i ⋅ M i ( x ) , w h e r e ∑ i = 1 n G ( x ) i = 1 \tilde{y} = {\textstyle \sum_{i=1}^{n}} G(x)_{i}·M_{i}(x),where {\textstyle \sum_{i=1}^{n}}G(x)_{i}=1 y~=∑i=1nG(x)i⋅Mi(x),where∑i=1nG(x)i=1
定义Gating Net G G G 的参数为 w i w_{i} wi( d 2 d_{2} d2维),门损失函数 p i p_{i} pi :
p i ( w i ) = E ( x , y ) ∼ D i [ L i ( y ~ , y ) ] p_{i}(w_{i})=\mathbb{E}_{(x,y)\sim\mathcal{D}_{i}} [L_{i}(\tilde{y} ,y)] pi(wi)=E(x,y)∼Di[Li(y~,y)]
其中 p i p_{i} pi : R d 1 → R \mathbb{R}^{d_{1}}\rightarrow\mathbb{R} Rd1→R, y ~ \tilde{y} y~可以表示为:
g = s i g m o i d ( G ( w i ; x ) ) g=sigmoid(G(w_{i};x)) g=sigmoid(G(wi;x))
y ~ = g ⋅ M G ( θ ; x ) + ( 1 − g ) ⋅ M G ( θ i ; x ) \tilde{y}=g·M_{G}(\theta;x)+(1-g)·M_{G}(\theta_{i};x) y~=g⋅MG(θ;x)+(1−g)⋅MG(θi;x)
g表示专家模型的混合比例,g为全局的权重,而1 - g为本地专家的权重。门控网络参数更新如下:
w i = w i − β ⋅ ▽ p i ( w i ) w_{i}=w_{i}-\beta·\bigtriangledown p_{i}(w_{i}) wi=wi−β⋅▽pi(wi)
B.PFL-MF
PFL- FB是一种基于冻结参数的局部适应PFL算法,属于PFL-DT的变式,它冻结联邦模型的基层,只微调最上层。根据PFL-MoE的三个步骤,本文提出了利用PFL-FB算法生成的本地专家的PFL-MF算法。
在PFL- FB中,全局模型结构 M G M_{G} MG 分为特征提取器 M E M_{E} ME 和分类器 M C M_{C} MC 两部分。定义 M E M_{E} ME和 M C M_{C} MC的参数分别为 θ E \theta_{E} θE 和 θ C \theta_{C} θC。在PFL-MF中, θ \theta θ 是全局模型参数,对于客户 i i i , ( θ E , θ C i \theta_{E},\theta_{C_{i}} θE,θCi) 由 θ \theta θ 进行初始化,其中 θ E \theta_{E} θE 由所有客户共享, θ C i \theta_{C_{i}} θCi 是是客户 i i i 的个性化分类器参数。
θ C i = θ C i − α ⋅ ▽ f i ( θ E , θ C i ) \theta_{C_{i}}=\theta_{C_{i}}-\alpha·\bigtriangledown f_{i}(\theta_{E},\theta_{C_{i}}) θCi=θCi−α⋅▽fi(θE,θCi)
f i ( θ E , θ C i ) = E ( x , y ) ∼ D i [ L i ( y ^ , y ) ] f_{i}(\theta_{E},\theta_{C_{i}})=\mathbb{E}_{(x,y)\sim\mathcal{D}_{i}} [L_{i}(\hat{y} ,y)] fi(θE,θCi)=E(x,y)∼Di[Li(y^,y)]
其中 a = M E ( θ E , x ) a=M_{E}(\theta_{E},x) a=ME(θE,x) and y ^ = M C ( θ C ; a ) \hat{y}=M_{C}(\theta_{C};a) y^=MC(θC;a)
在PFL-MF算法的混合阶段中,与上述不同的是,x对应的混合伪标号 y ~ \tilde{y} y~ 记为:
y ~ = g ⋅ M C ( θ C ; a ) + ( 1 − g ) ⋅ M C ( θ C i ; a ) \tilde{y}=g·M_{C}(\theta_{C};a)+(1-g)·M_{C}(\theta_{C_{i}};a) y~=g⋅MC(θC;a)+(1−g)⋅MC(θCi;a)
通过对Fashion-MNIST数据集的实验,作者发现PFL-MF能够实现良好的个性化,并保持良好的泛化能力。
C.PFL-MFE
由于简单线性网络的限制,当输入的是比较复杂的高维数据时,门控不能很好地工作。为了解决这个问题,本文提出了利用特征作为门控输入的PFL-MFE算法。在卷积神经网络中,基础层负责捕获一般特征,而深层负责分类。直观地说,与原始数据相比,这些特性是门控输入的更好选择。
PFL-MFE算法修改了PFL-MF算法的模型结构,改为以激活 a a a 作为门控输入:
g = s i g m o i d ( G ( w i ; a ) ) g=sigmoid(G(w_{i};a)) g=sigmoid(G(wi;a))
实验结果
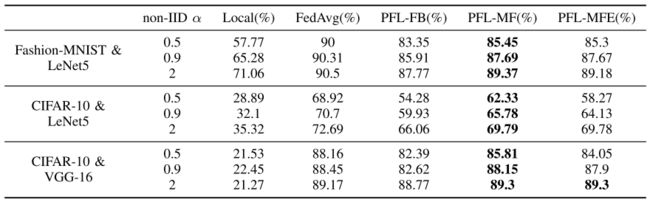
表一 :三个Baseline中所有客户端的局部测试精度的平均值,以及所提出的算法
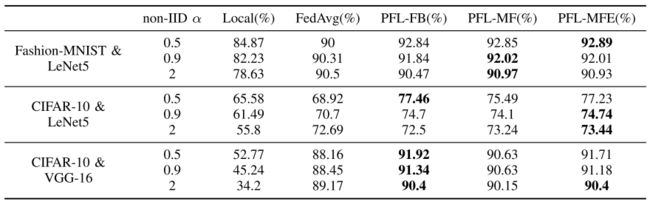
表二 :所有客户端全局测试精度的平均值:
在所有实验中,无论是大模型VGG-16还是小模型LeNet-5,局部测试和全局的准确率都低于FedAvg。在本地的CIFAR-10实验中,较大的模型VGG-16的精度特别低,明显低于较小的模型LeNet5。一般来说,模型越深,它的能力限制越高,但是训练需要更多的数据。虽然简单的模型在本地的性能相对较好,但它的局限性使客户更有动力参与联邦学习,以训练更强大的模型。
表二表明,三种PFL算法的平均全局测试精度要高于局部的,这意味着PLF可以有效提高模型在客户端的泛化能力。由表1可知,在α = 0.5时,这三种个性化算法的平均局部测试准确度比FedAvg高出2% ~ 10%。然而,PFL-FB更容易引起过拟合。当相对较大时,PFL-FB更容易对局部数据过度拟合,使得个性化的模型比全局模型更差。
在本文提出的PFL-MF算法中,如果个性化的模型出现恶化,将被门控网络直接丢弃。此外,门控网络已经知道哪些数据适合使用个性化模型,哪些数据需要更多地向全局模型倾斜。因此,PFL-MF更稳定,其局部测试精度始终高于FedAvg。
在FashionMNIST上的实验中,本文提出的PFL-MF算法在两次测试中均优于PFL-FB,表明PFL-MF比PFL-FB具有更好的个性化和泛化效果。
在CIFAR-10上的实验中,PFL-MFE比PFL-MF更有效,因为门控网络可以利用抽象特征间接做出更好的决策。对于简单的Fashion-MNIST数据集,PFL-MF就足够了。在保持PFL-MF优点的同时,PFL-MFE可以更好地识别复杂的输入数据。这也说明将特征替换直接输入能得到”更牢固“的门控网络模型。
3.文章总结
本文提出了PFL-MoE,一种基于混合专家模型的个性化联邦学习方法。PFL-MoE可以结合个性化模型和全局模型的优点,实现更好的个性化和更好的泛化。作为PFL-MoE的一个实例,PFL-MF在局部测试和全局测试中都比已有的算法PFL-FB表现得更好。实验结果表明,PFL-MFE增强了混合专家模型选通网络的决策能力,能够有效地处理复杂的数据。