复习C语言过程中的总结与思考(万字长文 + 思维导图,建议收藏)
内容长文,多图预警!!!
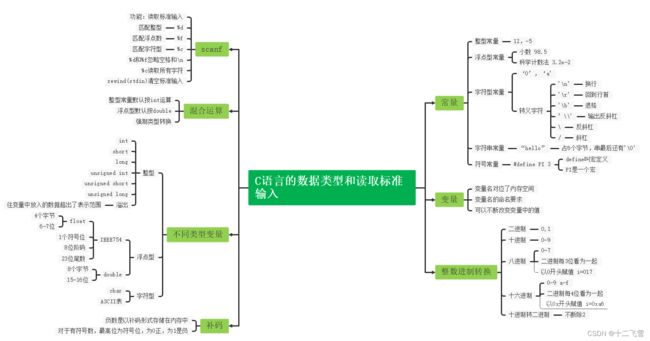
- 一、C语言的数据类型和读取标准
-
- 1. C语言中整数型**常量**的数据类型为int类型,例子如下:
- 2. C语言中浮点数型常量的数据类型为double类型
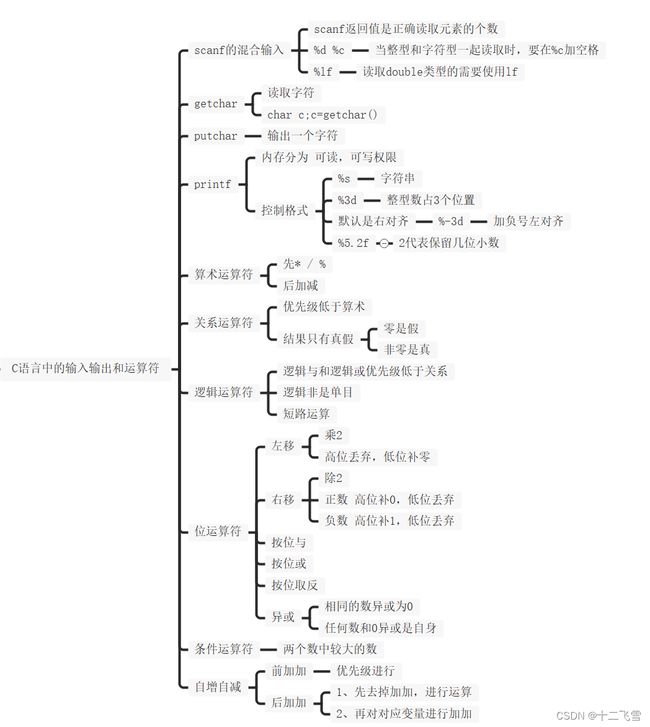
- 二、C语言中的输入输出及位运算符
-
- 1、scanf函数缓冲区和返回值
- 2、位运算
-
- 例1:字母大小写转换
- 例2、交换a、b的值
- 例3:找出数组中只出现一次的一个数
- 例4:找出数组中只出现一次的两个数(分治+位运算)
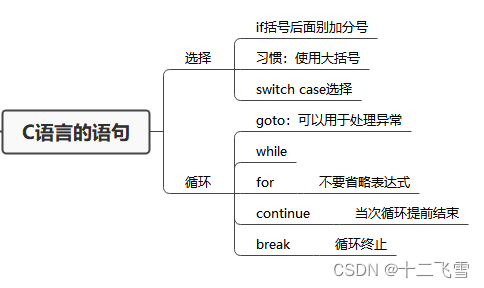
- 三、C语言的基本逻辑语句
-
- goto语句的巧用——异常处理
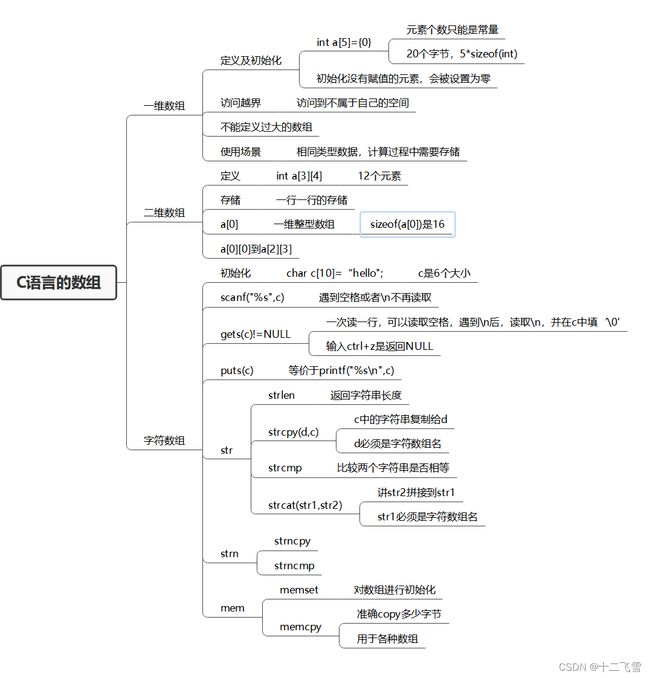
- 四、C语言的数组
-
- str、strn、mem系列函数
- 五、指针——C语言的灵魂,C语言对程序员的信任
-
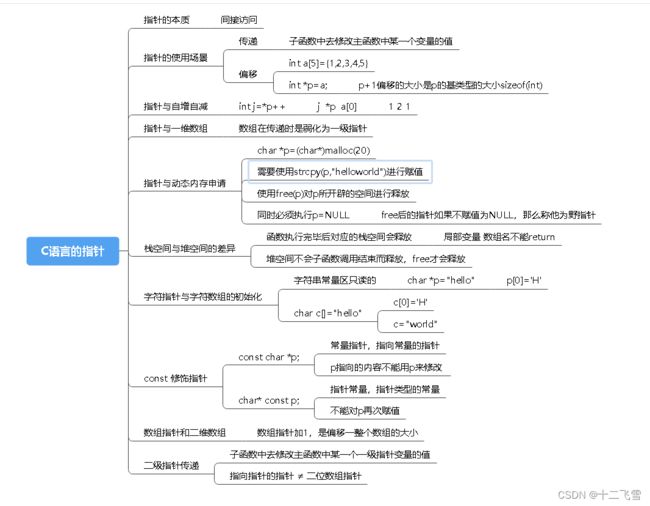
- 1、指针的本质
- 2、指针在函数中的传递
- 3、指针和数组
- 4、数组指针的思考
- 5、动态内存申请和野指针
- 6、堆和栈的区别——C语言中不同的内存区
- 7、字符数组和字符指针区别
- 8、const修饰符
- 9、手动实现memmove
- 10、数组指针、二维数组和二级指针理解
- 六、C语言的函数
-
- 1、头文件和函数调用
- 2、setjmp和longjmp
- 3、函数递归
- 七、结构体——将数据打包
-
- 1、结构体的定义及访问成员方法
- 2、结构体指针和结构体变量声明
- 3、typedef的使用
- 4、结构体实现单链表方法
- 5、共用体和枚举类型
- 6、题目:链表逆置
- 7、题目:查找倒数第n位的结点元素
- 8、题目:查找链表中间位置的结点元素
- 八、C语言文件操作
-
- 1、文件指针
- 2、文件的打开与关闭
- 3、文件的读与写
-
- 3.1 fputc函数和 fgetc函数
- 3.2 fread函数和 fwrite函数。
- 3.3 fgets函数和 fputs函数
- 3.4 fprintf函数和 fscanf函数
- 3.5 ftell函数
- 九、C语言预处理
-
- 1、宏定义
- 2、条件编译
- —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— ——
- 文章至此,非常感谢各位读者的耐心阅读,C语言的干货内容已经结束。接下来的内容是作者自己学习数据结构的代码练习,只做代码实现不做详细讲解,请读者自行决定去留。
- —— —— —— —— —— —— —— —— —— —— —— —— —— —— —— ——
- 十、C语言中常用数据结构与算法
-
- 1、数据结构 栈的实现
- 2、数据结构 队列的实现
- 3、数据结构 二叉树
- 十 一、C语言中常见的排序算法
-
- 1、冒泡排序
- 2、选择排序
- 3、插入排序
- 4、希尔排序
- 5、快速排序(递归)
- 6、堆排序
- 7、归并排序
- 8、计数排序
- 排序算法性能对比
- 十二、C语言中常见的查找算法
-
- 1、二分查找
- 2、哈希表
- 3、位图bitmap
- 待续..
- 红黑树补档
内容概述
笔者基于《龙哥教你学C语言》、《C陷阱与缺陷》补充一些C语言的问题和之前学习没有注意到的地方。好久没有写过文章了,这次写C的文章主要是为了复习C的语法,为了进一步学习C++打好基础。考虑到太长的文章读起来比较累,所以后续学习了《C和指针》、《C专家编程》考虑为本文继续补充或者再开新坑。
作者在撰写本文时已经学过C语言了,所以本文要求对C语言有一定基础,也对C语言中重点内容做一个复习,对之前的学习进行查漏补缺。每部分内容都会先放上思维导图用于复习C语言的语法内容。如果某些语法不记得了,可以在 C++ 菜鸟教程网站进行复习,那么开始吧。
如果各位前辈对本文中的问题感兴趣,可以在评论区互相讨论,互相学习。
系统环境
Microsoft Visual Studio 2013、2017、2019、2021均可 下载地址
一、C语言的数据类型和读取标准
1. C语言中整数型常量的数据类型为int类型,例子如下:
#include运行后发现变量 l 的值为0
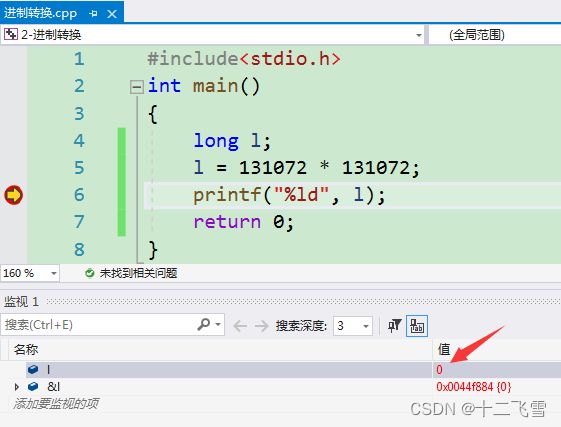
为什么会是0呢,这就和一开始所说的整数型常量是int类型有关了,打开程序员计算器输入131072,得到的二进制位0010 0000 0000 0000 0000,如下图中我们可以看到后四字节为0000 0000 0000 0000,int类型长度为4字节,即131072的int类型值为0,所以上述程序运行的实际上是l = 0*0;
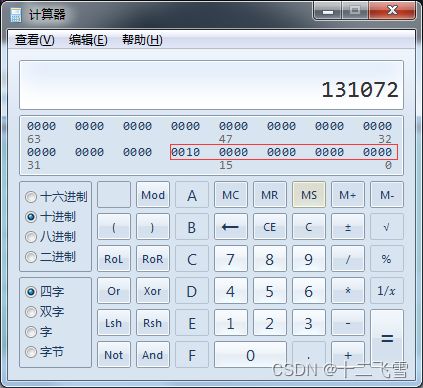
那么应该如何改动程序才可以获得我们想要的结果呢?没错,就是使用强制类型转换,正确写法如下。
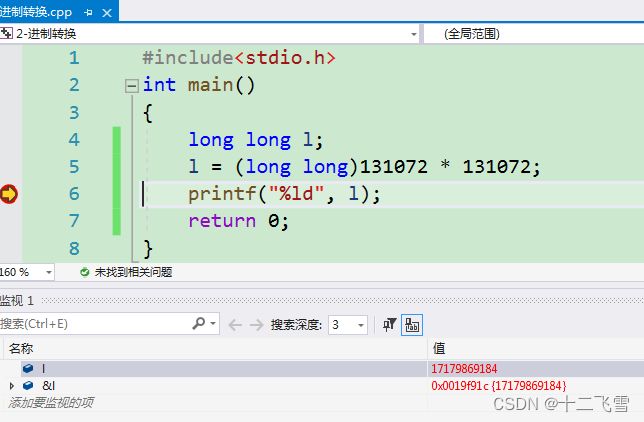
2. C语言中浮点数型常量的数据类型为double类型
double类型在C语言中按照IEEE854标准占据8字节存储双精度浮点数,可以表示的精度为6-7位小数。
下面看一个浮点数常量的案例:
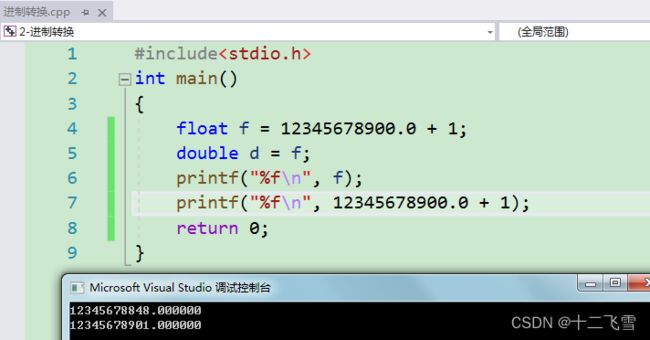
显然浮点型常数的精度比普通float类型的变量精度更高,原因就在于浮点数常量的数据类型为double类型。
二、C语言中的输入输出及位运算符
1、scanf函数缓冲区和返回值
scanf函数本质上是阻塞进程,等待键盘的输入,键盘输入的内容最终进入缓冲区,然后scanf再从缓冲区中读出。
如果刚输入一个整型再读入一个字符型,则打印出的字符变量什么都没有
scanf("%d",&i); //10
printf("%d",i); //10
scanf("%c",&c); //
出现这种情况的原因在于,读取字符的scanf将缓冲区中的'\n'换行符读入了,实际上变量c并非没有值,而是值为'\n',打印为换行符。
实际上,scanf在读取整型、浮点型、字符串类型时会忽略'\n'、空格符等字符,但在读取字符型时却无法忽略。
为了实现连续输入,VS(2013-2017)版本中的库中有这样一种函数fflush(stdin)清空标准输入缓冲区。用法如下:
while(fflush(stdin),scanf("%d",&i))!=EOF) {...}
如果使用上述写法读取字符,则会出现错误,导致缓冲区内的字符被清空,最终只能读入第一个输入的字符。
while(fflush(stdin),scanf("%c",&c))!=EOF) {...}
注:在VS2019版本中可以使用rewind(stdin);清空缓冲区,和fflush(stdin)写法稍有不同。例如:
scanf("%d",&a); //输入整型变量a
rewind(stdin); //清空缓冲区
scanf("%c",&c); //再读入字符变量c
此时,不会再出现c变量读入换行符'\n'的情况了
scanf函数的返回值含义是正确输入的字符个数
同样的,printf函数也有其返回值,含义为输出的字符个数
2、位运算
简单介绍一下C语言中的位运算,包括&(与)、|(或)、!(非)、^(异或)、>>(逻辑右移)、<<(逻辑左移)等几种。
这里不对上述位运算符做解释,网络上的语法教程也很多很详细,不做赘述,这里想借用几个案例来体现位运算的巧妙之处。
例1:字母大小写转换
看到这个问题,很多读者都会说简单,大写字母的ASCII 比小写字符的ASCII小32,直接减32就可以进行转换。这里呢笔者通过读王爽老师的《汇编语言》学到了新的方法。一般来说,位运算的速度要比逻辑运算快。那我们如何通过位运算来优化处理这个问题的过程呢?如下图。
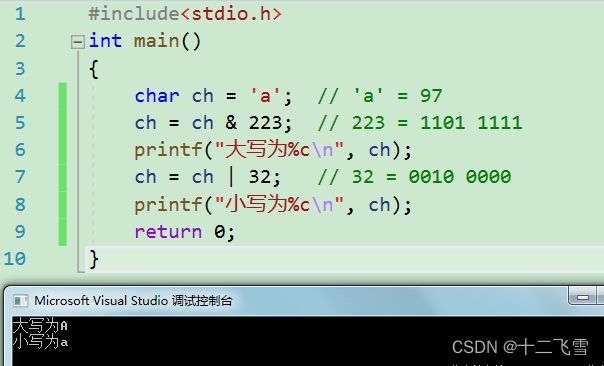
这里使用了位运算符实现了大小写转换的操作,代码中所用到的二进制数位如下:
a - 0110 0001
223 - 1101 1111
32 - 0010 0000
我们会发现当a和223按位与的操作结果就是a的第6位bit(从右向左)改为0,第6位的bit位含义刚好是2^5=32
实际上a和223按位与就是a-32 = 97-32 = 65,得到了A
同理a和32按位或的操作结果就是a的第6位bit(从右向左)改为1,第6位的bit位含义刚好是2^5=32
实际上A和32按位或就是A+32 = 65+32 = 97,得到了a
例2、交换a、b的值
- 交换两个变量的值,常规做法为声明一个变量tem,用tem作为中介值,交换a和b的值,写法如下:
//第一种交换方法:
int tem = a;
a = b;
b = tem;
- 上述的写法需要额外申请一个变量空间,耗费较大,我们还可以不申请额外的空间交换a和b的值,写法如下:
//第二种交换方法:
a = a+b;
b = a-b;
a = a-b;
- 利用a与b的合,使用减法的方法就可以交换a和b的值。这里抛出问题,既然可以使用加减的方式交换,那是否能用位运算符进一步优化代码呢?
//第三种交换方法:
a = a^b;
b = a^b;
a = a^b;
这里直接上代码,不太容易理解,举个例子,a = 0101(5),b = 0011(3)
a = a^b = 0110(6)
b = a^b = 0101(5)
a = a^b = 0011(3)
讲解一下原理,为什么异或就能交换变量a和b的值呢?这里涉及到离散数学中的知识点,首先我们要先了解异或运算的性质。
1、 任何数与自身异或为0 a^a = 0
2、 任何数与0异或为自身 a^0 = a
3、 异或运算具有结合律 a^b^c = (a^b)^c = a^(b^c)
4、 异或运算具有交换律 a^b = b^a
了解了性质后再把代码拆开了看,
a = a^b;
b = a^b = a^b^b = a; //根据交换律,b^b = 0, 然后a^0 = a;
a = a^b = a^b^a = b; //根据交换律,a^a = 0, 然后b^0 = b;
基于上述的异或的性质,再给出一个小案例——找出数组中只出现一次的数,请读者独立思考后阅读代码:
//找出数组中只出现一次的数
#include例3:找出数组中只出现一次的一个数
题目:101个数中有50个数出现了2次,1个数出现了1次,找出这一个数。
本题使用了位运算的第一条和第二条性质,即50*2个数异或后得到的结果为0,再用0与另一个数异或即可得出出现了一次的数。代码如下:
# include 例4:找出数组中只出现一次的两个数(分治+位运算)
这题在上一题的基础上进行了改进,即两个数只出现了一次,这时候就要用到了分治的思想,关键在于如何划分整个数组。
1. 对所有数进行异或得到result
2. 用result&(-result),可以得到result的最小为1的位数
3. 最后用此结果与整个数组按位与操作就可以划分出两堆
4. 两堆中分别有一个只出现一次的数,再对两堆进行异或操作即可
对于第一步,异或可以理解为找不同,找到这a、b两个数的不同即result,虽然此时不知道这两个数是什么。其次第二步,这个result的最低1位与a、b一个相同一个不同。这样不太容易理解,举几个例子看看:
10 对应 1010
6 对应 0110
6&10 对应 1100
可以看到第三位,即6&10的最低位1位分别与6的第三位和10的第三位,一个相同一个不同。这里我们就借助这种特点用于划分数组。
找出最低的1位:12&(-12) = 1100 & 0100 = 0100
紧接着将得出的结果与整个数组相与,由于6和10的第三位不同,所以用0100与整个数组相与必定可以把6和10分在两堆中
最后从两堆中分别异或找出数即可
#include 三、C语言的基本逻辑语句
goto语句的巧用——异常处理
如今C语言的学习过程中,一般不学习goto语句,最早可以追溯到荷兰计算机科学家Dijkstra提出的goto有害论。但是goto语句仍然可以实现一些有趣的操作,比如异常处理,goto语句可以使得某些语句不执行,直接跳转到报错的语句,案例如下:
#include 四、C语言的数组
str、strn、mem系列函数
str系列函数主要对字符串进行操作
strn系列函数在操作字符串的时候可以加长度参数
mem系列函数主要对内存中的内容进行操作
//引入头文件
#include五、指针——C语言的灵魂,C语言对程序员的信任
1、指针的本质
int a = 3;
int *p;
//或写作 int* p;
p = &a;//p指向a的地址
//直接访问
printf("%d",a);
//间接访问
printf("%d",*p);
2、指针在函数中的传递
void func(int *b)//b是形参,是一个整型指针的形参
{
*b = 5;
}
int main()
{
int a = 10;
printf("%d",a);// 10
func(&a);//&a是实参
printf("%d",a);// 5
return 0;
}
上述代码中,先打印10,再打印5,原因在于func函数将a的地址作为参数传入,对a地址所指向的内存单元进行了修改。
3、指针和数组
通过传入的参数来修改数组的值
void change(char *d)
{
*d = 'H';
d[1] = 'E';
*(d + 2) = 'L';
}
int main()
{
char c[10] = "hello";
char* p = c;
change(c);
puts(c); //HELlo
4、数组指针的思考
来看一个《C陷阱和缺陷》中的一个例子,下列代码中,使用了非常规方式访问了数组a的第二个元素。“事实上,由于*(a + i), (i + a)的含义一样,那么a[i]和i[a]的含义也是一样的,但我们决不推荐这样写。”——《C陷阱和缺陷》。
我们来分析一下,按照我们的惯性思维,a是数组,i是变量,i[a]应该是错误的语法,但实际上编译器可以识别并且打印出相同的结果,可以说明C语言中的数组实际上就是使用指针来访问数组,也就是说*(i+a)等价于i[a]。这是一个非常有趣的例子,虽然我们不会这样编写代码,但是对于加深指针的理解颇有帮助。
#include5、动态内存申请和野指针
在C语言中可以使用malloc函数进行内存空间申请分配,并且malloc函数申请的是堆空间,使用方法如下:
char* p;//无类型指针
p=(char*)malloc(5);//malloc分配的就是堆空间
strcpy(p, "hello");
puts(p);
free(p);
p = NULL;
关于为什么要在malloc后使用strcpy函数对其进行赋值,因为"hello"字符串是常量,编译器优化后,完全可以将整个赋值直接作为程序段,从而不占用额外的内存空间。而且必须使用strcpy。
关于指针p的释放中,如果只进行了free§,而不执行p = NULL;这样p就是野指针,野指针就是指不知道此指针会指向那一部分内存,而且野指针可能会造成内存泄漏,是非常严重的行为,一定要记得将指针置空。
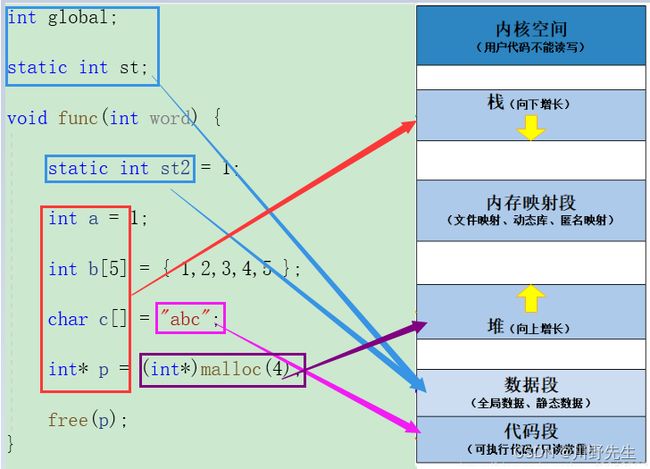
6、堆和栈的区别——C语言中不同的内存区
C语言中总共有5个区域,分别是栈区、堆区、常数区、静态区、代码区。
栈区:只在程序运行时出现,函数内部的变量、函数的参数以及返回值都会使用栈空间。栈空间在函数结束后由系统自动回收。
堆区:一般存放new或者malloc的对象,需要程序员使用delete或者free手动回收。堆空间不会因为函数执行结束而释放。
代码段:存放C语言程序编译后生成的可执行机器代码和只读常量。
常数区: 存放局部变量或者全局变量的值。
数据区: 用于存放全局变量或者静态变量。
7、字符数组和字符指针区别
字符指针所指向的内存空间是字符串常量,无法改变。
字符数组是一个数组,可以改变数组的值。
看一下例子:
char* p = "hello";
char c[10] = "hello";//等价于strcpy(c,"hello");
c[0] = 'H';//strcpy(c,"world");
//p[0] = 'H';不可以修改只读的字符串常量区,也不可以strcpy(p,"world");
p = "world";
puts(p);//可以修改,打印world
//c = "world";不可以的
puts(c);
8、const修饰符
const所修饰的变量不可改变,const修饰的指针所指向的空间也是不可变的。
char str[] = "hello world";
char str1[] = "how do you do";
char* const p=str;//p不可以再指向别的地方
p[0] = 'H';
puts(p);
9、手动实现memmove
通过指针的方式移动内存中的数据,即实现memmove函数代码如下:
#define _CRT_SECURE_NO_WARNINGS
#include 10、数组指针、二维数组和二级指针理解
- 数组指针:指向数组的指针,可以将数组赋值给数组指针。例子如下:
#include - 二级指针:指向指针的指针,不等于二维数组。
接下来看一个函数传递二级指针和一级指针交换值的例子:
#include 最终的结果就是将指针pj 指向的数值赋值给了指针pi所指向的值。
分析首先来看一下函数的形参,分别是二级指针和一级指针,而函数的实参呢,则传递了指针pi的地址,和指针pj。
传入指针pi的地址,实际上就是传递了指向指针pi的指针,就是二级指针,所以函数的形参使用了**pi,然后再将pj指针赋值给*pi。
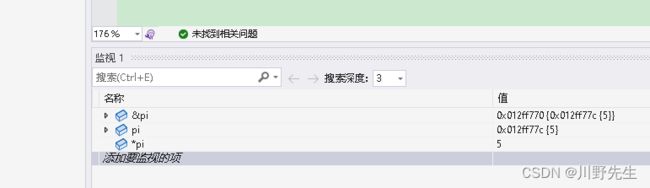
当我使用debug模式,对变量进行监控时可以发现,pi存放数值5,pi存放数值5所在的地址,&pi存放的就是pi的地址,相信到这里就可以很好理解二级指针和一级指针的关系了,其内容与《计算机组成原理》中的直接寻址和简介寻址相似,请读者好好体会。
- 二级指针和指针数组
char* p[5];
char b[5][10] = { "chinese","math","Java","python","c" };
char** p2;
for (int i=0;i<5;i++){
p[i] = b[i];//p[0]是字符指针类型,b[0]一维字符数组的数组名
}
p2 = p;//&p[0]--p内部所存储的指针类型是二级指针
上述代码中,将**p[i]=b[i]**的操作实际上是让指针数组p的每一个元素指向二维字符数组b的每一行首地址。并且p2是二级指针,指向指针数组p的首地址。
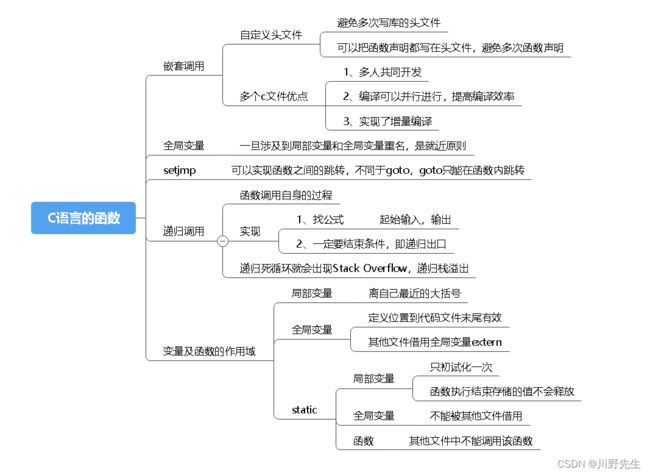
六、C语言的函数
1、头文件和函数调用
前面思维导图中讲到了,头文件的优点避免多次重写声明,多个c文件的优点在于可以使得多人协同开发系统,对程序进行多人分工模块化开发,使得程序的各个函数功能清晰,开发效率大大提升。下面给出一个例子,例子中包含func.h、func.c和main.c文件,体现了头文件、多个c文件以及函数之间互相调用的体现。
- 自定义头文件,将函数声明和引入系统头文件都放在此文件中。
//func.h是自定义头文件
#include - 自定义c文件,引入头文件,对头文件中定义的函数进行具体描述。
#include "func.h"
//函数的定义,也叫函数实现
int printStar(int i,int j)
{
printf("******************\n");
printf("printStar i=%d\n", i);
return i + 3;
}
void printMessage()
{
printf("how do you do\n");
printStar(5,3);
}
- 唯一的程序入口主函数,引入头文件,并且可以调用其他c文件中的函数。
#include "func.h"
int main()
{
printMessage();
printStar(2, 3);
return 0;
}
2、setjmp和longjmp
在C语言中函数内跳转需要使用goto语句,从一个函数跳转到另一个函数就需要使用setjmp和longjmp。这里做一点知识拓展,在汇编语言中由short jmp和long jmp用于进行跳转,类似于goto。也许C语言中做了更详细的区分,在过去的学习中,我几乎没有使用过setjmp和longjmp,应用场景不是很多,作为了解即可。给出书上的案例:
#include 3、函数递归
递归是指函数调用其自身的行为,要注意的是递归必须有递归出口,即结束掉递归的条件,否则会出现栈溢出的情况。前面讲了栈区存放的是函数内部的变量,如果无限次调用自身的函数,其中的变量并不会被重新定义,而是会再次申请栈区的空间,知道栈区满了,报出Stack Overflow的错误。
- 求阶乘的递归函数,输入一个较大的n,会反复调用自身,函数的参数和返回值都会占用栈区空间,每调用一次就会在申请一次栈区空间,直到当前的递归退出才会释放栈区空间。
//递归调用深度过大,会出现stack overflow
int f(int n)
{
if (1 == n) {//结束条件,递归出口
return 1;
}
return n * f(n - 1);
}
- 递归相较于循环的好处,递归的表达式相较于循环的逻辑简单,但是递归深度越深所占用的空间即栈区就会越多。
以下例子分别使用递归和循环的方式实现斐波那契函数。除此之外,递归的方式在树型数据结构中使用很多,极大简化了代码的复杂程度。
#include 七、结构体——将数据打包
1、结构体的定义及访问成员方法
C语言的结构体实现了将数据封装在一起的效果,即将数据打包,如下结构体基本使用的例子帮助复习。
//定义一个student结构体
struct student
{
int num;
char name[20];
char sex;
};
int main()
{
//初始化结构体
struct student s = { 101,"lele",'m' };
//结构体指针
struct student* p;
//结构体数组
struct student sarr[3] = { 1001,"lilei",'M',1005,"zhangsan",'M',1007,"lili",'f' };//
p = &s;
//通过结构体指针去访问每一个成员
//通过 -> 的方式
printf("%d %s %c\n", p->num, p->name, p->sex);
//通过 . 的方式
printf("%d %s %c\n", (*p).num, (*p).name, (*p).sex);
p = sarr;
printf("num=%d,p->num=%d\n",p++->num,p->num);
//打印1001和1005
return 0;
}
2、结构体指针和结构体变量声明
笔者在学习这部分内容,结构体指针和变量以及定义时声明的方法总是弄混,重新整理一下。我们在定义时声明结构体变量,会自动为这个结构体分配内存空间。当然了如果声明的是结构体指针,也会为指针分配内存,但不会为指针所指向的内容分配空间。看一下如下例子:
//带有一个成员变量的stu结构体
struct stu{
int n;
}s1,*p;
此处在定义结构体时声明了一个结构体变量和一个结构体指针变量
接下来我们分别来访问结构体变量和结构体指针变量
//为结构体成员赋值,并且打印
s1.n = 10;
printf("%d",s1.n);
//为结构体指针所指向的成员赋值,并且打印
p->n = 100;
printf("%d",p->n);
显然第二种写法错误,无法赋值,也无法打印我们想要的结果。问题就出在,定义时只是声明了一个结构体指针,仅仅是一个指针,什么都没有。如果我们想要得到正确结果,有两种写法:
- 第一种写法:p = &s1; 这样p就指向了s1,就可以使用p对s1进行操作了。
p = &s1;
p->n = 100;
printf("%d",p->n);
- 第二种写法:使用malloc分配内存空间。
p = malloc(sizeof(stu));
p->n = 10;
printf("%d",p->n);
- 特别提醒1:如果结构体的成员变量有指针类型同样需要为其分配内存空间
特别提醒2:如果是typedef struct定义结构体类型,需要在malloc前进行正确的强制转换,因为即便是指针指向了正确的位置,但如果指针指向的数据类型错误,那么访问成员变量就会出现问题。
typedef struct stu
{
char name[10];//数组不用再分配
char *sex;//指针类型需要分配空间,必要时记得回收
}stu;
int main()
{
stu *st;
st=(stu *)malloc(sizeof(stu));
st->sex=(char*)malloc(sizeof(char)*1);
strcpy(st->name,"zhangsan");
scanf("%s",st->sex);
}
3、typedef的使用
typedef可以自定义新类型,同样可以将结构体也作为新的类型名,例子如下:
typedef int ELEMTYPE;
//不要让变量名和结构体类型重名
//比如typedef int int;没有必要
int main()
{
ELEMTYPE i;
scanf("%d", &i);
printf("%d", i);
return 0;
}
typedef将结构体作为类型名的例子,代码如下:
typedef struct student
{
int num;
char name[20];
char sex;
}stu,*pstu;
int main()
{
stu s = { 101 };
pstu p;
return 0;
}
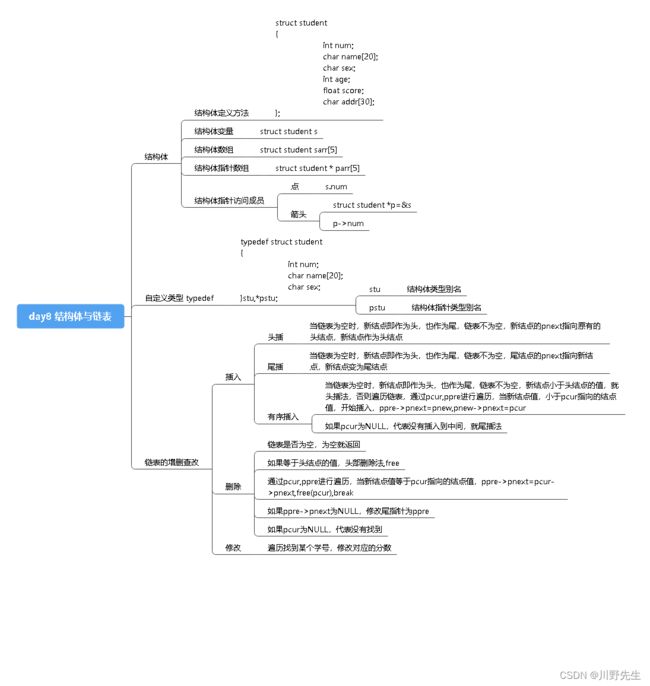
4、结构体实现单链表方法
单链表是非常重要的数据结构,包含单链表定义、初始化、头插法、尾插法、顺序插入、链表删除和链表修改。
由于网上关于单链表的内容很多,这里不做赘述,只给出代码,以供复习。
- 头文件func.h
#include- 函数实现文件func.c
#include"func.h"
// 头插法
// 此处LinkList* 和 LNode**含义相同,参考前面一级指针和二级指针的内容
void list_head_insert(LinkList* pphead, LNode** pptail, ElemType i)
{
//1、申请结点空间,并初始化
LinkList node = (LinkList)malloc(sizeof(LNode));
node->num = i;
node->pnext = NULL;
//2、当链表为空时,新结点就是头结点,同时也是尾结点
if (*pphead == NULL) {
*pphead = node;
*pptail = node;
}
//3、当链表不空时,将新结点作为新的头结点
else {
node->pnext = pphead;
*pphead = node;
}
}
//尾插法
void list_tail_insert(LinkList* pphead, LNode** pptail, ElemType i)
{
//1、申请结点空间,并初始化
LinkList node = (LinkList)malloc(sizeof(LNode));
node->num = i;
node->pnext = NULL;
//2、当链表为空时,新结点就是头结点,同时也是尾结点
if (*pphead == NULL) {
*pphead = node;
*pptail = node;
}
//3、当链表不空时,将新结点作为新的尾结点
else {
(*pptail)->pnext = node;
*pptail = node;
}
}
//顺序打印
void list_print(LinkList phead) {
while (phead) {
printf("%3d %5.2f\n", phead->num, phead->score);
phead = phead->pnext;
}
printf("\n");
}
//顺序插入
void list_sort_insert(LinkList* pphead, LinkList* pptail, ElemType i)
{
//1、申请结点空间,并初始化
LinkList node = (LinkList)malloc(sizeof(LNode));
node->num = i;
node->pnext = NULL;
LinkList pre, p;//当前结点p和前驱结点pre,方便插入
pre = p = *pphead;
//2、当链表为空时,新结点就是头结点,同时也是尾结点
if (*pphead == NULL) {
*pphead = node;
*pptail = node;
}
//3、当头结点的值大于i时,插入在头部作为头结点
else if (p->num > node->num) {
node->pnext = p;
*pphead = node;
}
//4、插入在中间的情况
else {
//顺序遍历
while (p) {
if (p->num > node->num) {
pre->pnext = node;
node->pnext = p;
return;//插入成功就退出
}
pre = p;
p = p->pnext;
}
//如果上述循环没有退出,应该将node插入到结尾处
(*pptail)->pnext = node;
*pptail = node;
}
}
//删除结点
void list_delete(LinkList* pphead, LinkList* pptail, ElemType i)
{
LinkList pre, p;
pre = p = (*pphead);
//1、如果删除的结点在头部
if (p->num == i) {
*pphead = pre->pnext;
//如果删除链表中唯一结点,则将尾指针置为NULL
if (*pphead == NULL) {
*pptail = NULL;
}
free(p);//释放空间,应该置为NULL
p = NULL;
}
//2、如果删除的结点在中间或者尾部
else {
while (p) {
if (p->num == i) {
pre->pnext = p->pnext;
free(p);
p = NULL;//释放结点要制空
break;
}
pre = p;
p = p->pnext;
}
//3、删除的结点是尾结点,修改尾指针
if (pre->pnext == NULL) {
*pptail = pre;
}
//4、未找到的情况
if (p == NULL) {
printf("未找到");
return;
}
}
}
//链表修改
void list_modify(LinkList phead, ElemType i, float score)
{
while (phead != NULL) {
if (phead->num == i) {
phead->score = score;
}
phead = phead->pnext;
}
if (phead == NULL) {
printf("未找到");
}
}
- 主函数调用源.c
#include "func.h"
int main()
{
LinkList phead = NULL, ptail = NULL;
ElemType i;
while (scanf("%d", &i) != EOF)
{
//list_head_insert(&phead, &ptail, i);
//list_tail_insert(&phead, &ptail, i);
list_sort_insert(&phead, &ptail, i);
}
list_print(phead);
//while (printf("请输入删除结点值\n"), scanf("%d", &i) != EOF)
//{
// list_delete(&phead, &ptail, i);
// list_print(phead);
//}
float f;
while (scanf("%d%f", &i, &f) != EOF)
{
list_modify(phead, i, f);//输入对应学号,修改它的成绩
list_print(phead);
}
return 0;
}
5、共用体和枚举类型
- 共用体union,和结构体十分类似,但又有很多不同之处。首先共用体中的成员变量共用一片存储区域,并且共用体的最大长度为成员变量中最大的类型。如果对共用体的成员变量进行赋值会影响到其他的成员变量,至于如何影响则需要观察内存了。
union data
{
int i;
char ch;
float f;
};
union data a;//共用体也叫联合体
a.i = 10;
a.ch = 'm';
a.f = 98.2;
- 枚举类型,枚举型是预处理指令#define的替代,枚举和宏其实非常类似。枚举类型有一个特点,如果不对其成员变量赋初值,那么其成员变量的值从0依次递增。如果对其中之一赋了初值,那么后面的会在此基础上递增。例子如下:
enum weekday
{
sun,mon,tue=5,wed,thu,fri,sat
};
//这里的变量的结果为0,1,5,6,7,8,9
6、题目:链表逆置
使用带有头结点的链表,使用头插法进行原地逆置。链表定义与上文相同只给出函数,代码如下:
//逆序(头结点方式):实际上就是取下链表头,将后面的元素头插法即可
void reverse(pLNode* phead) {
pLNode p = (*phead)->next;
(*phead)->next = NULL;
pLNode tem;
while (p) {
tem = p; //使用tem摘下结点
p = p->next; //p后移
tem->next = (*phead)->next; //将tem结点插入到phead后面
(*phead)->next = tem;
}
}
7、题目:查找倒数第n位的结点元素
设置双指针1和2,指针2先走n-1步,然后两个指针同步前进,直到指针2到尾部,此时指针1就为倒数第n的结点。
- 第一步:设置指针p和q,q向后移动n个,假设n为3,此时p指向1,q指向3。
p q
1 2 3 4 5 6 7 8 9 - 第二步:指针p和q同步后移,直到q指到尾部
p q
1 2 3 4 5 6 7 8 9 - 此时p所指的结点就为倒数第3的结点,具体函数代码如下:
//查找倒数第n的结点(链表带有头结点)
void func(pLNode* phead, int n) {
pLNode p = (*phead)->next;
pLNode q = (*phead)->next;
for (int i = 0; i < n-1; i++) {
q = q->next;
}
printf("倒数第%d的元素为%d", n, p->val);
while (q) {
p = p->next;
q = q->next;
}
printf("倒数第%d的元素为%d", n, p->val);
}
8、题目:查找链表中间位置的结点元素
与上题相似,设置双指针1和2,不过使用快慢指针的方式可以得到中间元素。指针1每次走1步,指针2每次走2步,当指针2走到链表尾部的时候,指针1刚好指向链表的中间结点。代码如下:
//找到链表中位于中间的结点元素
void func(pLNode* phead) {
//设置快慢指针,慢指针p一次走1步,快指针q一次走2步
pLNode p = (*phead)->next;
pLNode q = (*phead)->next;
while (q->next != NULL) {
p = p->next;
q = q->next->next;
}
printf("中间结点元素为:%d", p->val);
}
八、C语言文件操作
1、文件指针
打开文件后,我们会得到一个FILE的文件指针,然后通过文件指针对文件进行读写操作,文件指针是一个结构体,结构体如下:
struct _iobuf {
char *_ptr;
int _cnt;
char *_base;
int _flag;
int _file;
int _charbuf;
int _bufsiz;
char *_tmpfname;
};
typedef struct _iobuf FILE;
FILE* pf;//文件指针变量
pf是一个指向文件指针,我们可以通过对文件指针的成员变量进行操作来访问文件。
2、文件的打开与关闭
fopen函数用于打开文件,并返回一个关联该文件的流。如果发生错误,fopen返回NULL。
fopen的函数定义如下:FILE *fopen(const char *fname,const char *mode);
fclose函数用于关闭给出的文件流,并释放缓冲区。fclose执行成功返回0,失败返回EOF。
fclose的函数定义如下:int fclose(FILE *stream);
常用的mode参数如下:
| mode(方式) | 意义 |
|---|---|
| “r” | 打开一个用于读取的文本文件 |
| “w” | 创建一个用于写入的文本文件 |
| “a” | 附加到一个文本文件 |
| “rb” | 打开一个用于读取的二进制文件 |
| “wb” | 创建一个用于写入的二进制文件 |
| “ab” | 附加到一个二进制文件 |
| “r+” | 打开一个用于读/写的文本文件 |
| “w+” | 创建一个用于读/写的文本文件 |
| “a+” | 打开一个用于读/写的文本文件 |
| “rb+” | 打开一个用于读/写的二进制文件 |
| “wb+” | 创建一个用于读/写的二进制文件 |
| “ab+” | 打开一个用于读/写的二进制文件 |
//测试打开关闭文件
#define _CRT_SECURE_NO_WARNINGS
#include3、文件的读与写
3.1 fputc函数和 fgetc函数
fputc函数用于将字符ch的值输出到fp所指的文件中,如果成功,返回输出的字符数量,失败返回EOF。
fputc的函数定义如下:int fputc(int ch, FILE *stream);
fgetc函数用于从指定文件中读入一个字符,该文件必须是以读或者读写的方式打开的。
fputc的函数定义如下:int fgetc(FILE *stream);
//测试fclose和fgetc读写文件
//向文件中写入一串字符串
char sent[] = "what's your name?";
int i = 0;
while (sent[i] && i < strlen(sent)) {
fputc(sent[i], fp);
i++;
}
//从文件中读出一串字符
char c;
while ((c = fgetc(fp)) != EOF)
{
putchar(c);
}
当我信心慢慢地编写了如下代码:心怀期待地等待读出结果,结果啥也没有,然后我突然想到了一个问题,对于文件中的内容读写实际上是用指针在操作,那么我写完字符串后,指针是否就停留在了末尾,然后读文件的时候从末尾开始,所以就没有任何结果。
带着问题做验证,我先用了一个比较笨的方法,关闭再打开文件,重新进行读操作,确实如此。重新打开文件后,文件指针回到了开头就又可以读取文件内容了。那么我如何操作读写文件的指针呢?这里的问题先按下不表,我们先学习第二种读写方式再来处理这个问题。
3.2 fread函数和 fwrite函数。
fread函数用于从给定流 stream 读取数据到 ptr 所指向的数组中。
fread的函数定义如下:int fread(void *buffer, size_t size, size_t num, FILE *stream);
fwrite函数用于把 ptr 所指向的数组中的数据写入到给定流 stream 中。
fwrite的函数定义如下:int fwrite(const void *buffer, size_t size, size_t count, FILE *stream);
这里必须处理上面遗留的问题了,否则fwrite函数还会出现和fgetc函数一样的情况,介绍两个函数分别是rewind函数和fseek函数。
fseek函数用于设置流 stream 的文件位置为给定的偏移 offset,参数 offset 意味着从给定的 whence 位置查找的字节数,第三个参数可以为SEEK_SET: 文件开头,SEEK_CUR: 当前位置,SEEK_END: 文件结尾。
fseek的函数定义如下:int fseek(FILE *stream, long offset, int fromwhere);
rewind函数用于设置文件位置为给定流 stream 的文件的开头。
rewind的函数定义如下:int rewind(FILE *stream);
//测试fread和fwrite读写文件
char sent[] = "what's your name?";
fwrite(sent, sizeof(char), sizeof(sent), fp);
//从文件中读出一个字符
//重置文件读写指针到开头
//rewind(fp);
//将文件读写指针从当前位置偏移-17整个数组长度的位置,即文件开头
//fseek(fp, -17, SEEK_CUR);
fseek(fp, 0, SEEK_SET);
fread(sent, sizeof(char), sizeof(sent)-1, fp);
printf("%s", sent);
上述代码中rewind和fseek函数的效果等价,读者可以自行尝试。
3.3 fgets函数和 fputs函数
fgets函数从指定的流 stream 读取一行,并把它存储在 str 所指向的字符串内。当读取 n-1个字符,或读取到换行符,或到达文件末尾时,就会停止。
fgets的函数定义如下:char *fgets(char *str, int n, FILE *stream)
fputs函数把字符串写入到指定的流 stream 中,但不包括空字符。
fputs的函数定义如下:int fputs(const char *str, FILE *stream)
//fgets函数和fputs函数的测试
#include 3.4 fprintf函数和 fscanf函数
fprintf函数,用于发送格式化输出到流 stream 中。
fprintf的函数定义如下:int fprintf(FILE *stream, const char *format, ...)
//fprintf的测试
#include fscanf函数,用于从流 stream 读取格式化输入。
fscanf的函数定义如下:int fscanf(FILE *stream, const char *format, ...)
//fscanf的测试
#include 3.5 ftell函数
ftell函数,返回给定流 stream 的当前文件位置。
ftell 的函数定义如下:long int ftell(FILE *stream)
九、C语言预处理
1、宏定义
宏定义的格式如下 #define 标识符 替换列表,宏定义需要注意两个错误:
- 一种常见的错误是在宏定义中使用 “=”
#define N = 1024
int a[N]; //会被解释为int a[=1024]
- 第二个常见错误是末尾使用分号
#define N 1024;
int a[N]; //会被解释为int a[1024;]
我们可以使用宏定义给数字、字符值和字符串值命名,如下:
#define N 1024
#define TRUE 1
#define FALSE 0
#define sent "hello,world"
使用#define有许多显著的优点:
- 提高代码可读性
- 宏定义易于修改
- 可以对C语法做小的修改。
- 对类型进行重命名
带参数的宏定义
可以定义如下形式的宏定义:
#define MAX(x,y) ((x)>(y)?(x):(y))
#define ISEVEN(n) ((n)%2==0)
为什么要加这么多括号呢?因为在使用宏定义的时候,预处理器直接宏定义的部分替换。举个例子:
#define ISEVEN(n) ((n)%2==0)
ISEVEN(i)+3的含义是((i)%2==0)+3
#define ISEVEN(n) n%2==0
ISEVEN(i)+3的含义是 i%2==0+3
不加括号设定优先级就无法得到我们想要的结果,所以在使用宏定义的时候需要小心。
const 和宏定义的区别
- 编译器处理方式不同。define在预处理阶段进行,const在编译运行阶段进行。
- 类型和安全检查不同。define宏没有类型,不做检查,仅做替换展开。const有具体类型,编译阶段会检查类型。
- 存储方式不同。define仅展开,不会分配内存。const会在内存中分配。
- 使用const可以避免不必要的内存分配。
- const定义常量从汇编的角度来看只是给出了变量的地址,define则是给出立即数,define定义的常量在内存中有若干副本。
- const的销量更高。因为const变量是常量,没有读写内存的操作。
2、条件编译
#if 指令和 #end if 指令
上述两条指令方便调试:
#define DEBUG 1
#if DEBUG
printf("hello");
#endif
如果DEBUG的值为0,则预处理器会将printf函数保留在程序中执行。如果DEBUG的值为0并重新编译,那么预处理器会将这4行代码都删除,即不运行。
#ifdef 指令和 #ifndef 指令
#ifdef 指令用于测试一个标识符是否已经定义成宏。
#ifndef指令与#ifdef相似,不过#ifndef用于测试一个标识符是否未被定义为宏。
—— —— —— —— —— —— —— —— —— —— —— —— —— —— —— ——
文章至此,非常感谢各位读者的耐心阅读,C语言的干货内容已经结束。接下来的内容是作者自己学习数据结构的代码练习,只做代码实现不做详细讲解,请读者自行决定去留。
—— —— —— —— —— —— —— —— —— —— —— —— —— —— —— ——
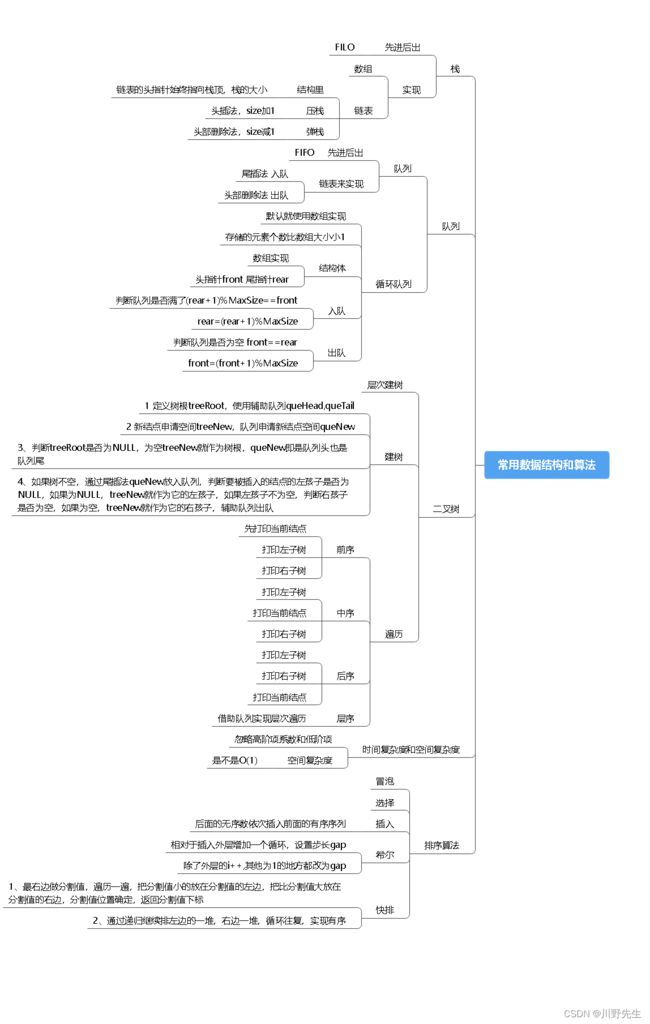
十、C语言中常用数据结构与算法
1、数据结构 栈的实现
栈数据结构的特点是先进先出,只在一段进行操作,并设有栈顶指针始终指向栈顶元素。共享栈正是基于栈数据结构所设立。
- 头文件stack.h—— 定义数据结构,声明函数
#include- stack.c ——实现函数
#include"stack.h"
//初始化链栈
void init_stack(pStack stack)
{
stack->phead = NULL;
stack->size = 0;
}
//出栈操作需要判断栈是否为空
int pop(pStack stack)
{
int tem;
//1.判断栈是否为空
if (stack->size == 0) {
printf("栈为空");
}
//2.栈不空,从链表头删除一个结点
else {
pNode p = stack->phead;
stack->phead = p->next;
tem = p->num;
free(p);
p = NULL;
stack->size--;
return tem;
}
}
//入栈操作使用头插法
void push(pStack stack, int val)
{
pNode p = (pNode)malloc(sizeof(Node));
p->num = val;
p->next = NULL;
//1.栈为空时,p成为第一结点入栈
if (stack->size == 0) {
stack->phead = p;
}
else {
p->next = stack->phead;
stack->phead = p;
}
stack->size++;
}
//取栈顶指针
int GetTop(pStack stack)
{
//1.判断栈是否为空
if (!stack->phead)
{
printf("stack is empty\n");
return -1;
}
//2.如果栈非空则返回第一个结点的值
else {
return stack->phead->num;
}
}
//判断栈空
int IsEmpty(pStack stack)
{
if (!stack->phead) {
printf("栈空");
return 0;
}
else {
printf("栈非空");
return 1;
}
}
//获取栈大小
int GetSize(pStack stack)
{
return stack->size;
}
- 源.c ——测试
#include"stack.h"
int main()
{
Stack s;
init_stack(&s);
push(&s, 10);
push(&s, 5);
printf("stack top val=%d\n", GetTop(&s));
pop(&s);
pop(&s);
printf("stack is empty?%c\n",IsEmpty(&s) ? 'Y' : 'N');
return 0;
}
int stack[100];
int top = -1;
2、数据结构 队列的实现
队列的数据结构特点是先进先出,并设有队头和队尾,在线性表的两端进行操作。双端队列、循环队列等数据结构在队列的基础之上作为改进。本文主要介绍循环队列,循环队列相对于普通队列,优点在于空间可重复使用。代码如下:
- 头文件queue.h—— 定义数据结构,声明函数
#include- queue.c——实现函数
#include"queue.h"
//初始化循环队列
void initQueue(SqQueue* Q)
{
Q->front = Q->rear = 0;
}
//判断队列是否为空
int IsEmpty(SqQueue* Q)
{
if (Q->front == Q->rear) {
printf("队空\n");
return 1;
}
else {
printf("队不空\n");
return 0;
}
}
//进队操作
int EnQueue(SqQueue* Q, ElemType x)
{
//1. 判断队满
if ((Q->rear + 1) % MaxSize == Q->front) {
printf("队满无法入队\n");
return 0;
}
//2. 队不满正常插入
else {
Q->data[Q->rear] = x;
Q->rear = (Q->rear + 1) % MaxSize;
printf("%d入队成功\n",x);
return 1;
}
}
//出队操作
int DeQueue(SqQueue* Q, ElemType* x)
{
//1.判读队空
if (IsEmpty(Q)) {
printf("队空,无法出队\n");
return 0;
}
//2.队不空正常出
else {
*x = Q->data[Q->front];
Q->front = (Q->front + 1) % MaxSize;
printf("%d出队成功\n", *x);
return 1;
}
}
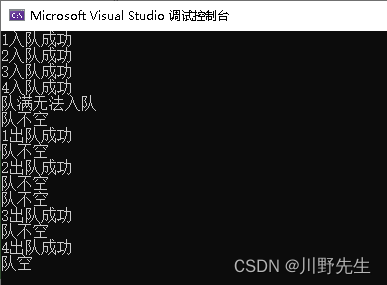
- 源.c——调用函数进行验证
#include"queue.h"
int main()
{
SqQueue Q;
initQueue(&Q);
int x;
EnQueue(&Q, 1);
EnQueue(&Q, 2);
EnQueue(&Q, 3);
EnQueue(&Q, 4);
EnQueue(&Q, 5);
DeQueue(&Q, &x);
DeQueue(&Q, &x);
IsEmpty(&Q);
DeQueue(&Q, &x);
DeQueue(&Q, &x);
IsEmpty(&Q);
return 0;
}
3、数据结构 二叉树
二叉树是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树,且有左右之分。
- 头文件tree.h—— 定义数据结构,声明函数
#define _CRT_SECURE_NO_WARNINGS
#include - tree.c——实现函数
#include "tree.h"
//建树
void buildBinaryTree(pNode_t* treeRoot, pQueue_t* queHead, pQueue_t* queTail, ElemType val)
{
//给树结点申请空间
pNode_t treeNew = (pNode_t)calloc(1, sizeof(Node_t));
treeNew->c = val;
pQueue_t queNew = (pQueue_t)calloc(1, sizeof(Queue_t));
queNew->insertPos = treeNew;
pQueue_t queCur;
//判断树是否为空
if (NULL == *treeRoot)
{
*treeRoot = treeNew;
*queHead = queNew;
*queTail = queNew;
}
else {
//入队
(*queTail)->pnext = queNew;
*queTail = queNew;
//判断某个树结点的左孩子是否为空,放入左边
if (NULL==(*queHead)->insertPos->left)
{
(*queHead)->insertPos->left = treeNew;
}
else if (NULL == (*queHead)->insertPos->right)判断某个树结点的右孩子是否为空
{
(*queHead)->insertPos->right = treeNew;
//当某个树结点左右孩子都有了,出队
queCur = *queHead;
*queHead = queCur->pnext;
free(queCur);
queCur = NULL;
}
}
}
//前序遍历,深度优先遍历
void preOrder(pNode_t treeRoot)
{
if(treeRoot)
{
putchar(treeRoot->c);
preOrder(treeRoot->left);
preOrder(treeRoot->right);
}
}
//中序遍历
void midOrder(pNode_t treeRoot)
{
if (treeRoot)
{
midOrder(treeRoot->left);
putchar(treeRoot->c);
midOrder(treeRoot->right);
}
}
//后续遍历
void latOrder(pNode_t treeRoot)
{
if (treeRoot)
{
latOrder(treeRoot->left);
latOrder(treeRoot->right);
putchar(treeRoot->c);
}
}
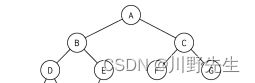
- 主函数源.c
#include "tree.h"
int main()
{
ElemType val;
pNode treeRoot = NULL;
pQueue queHead = NULL, queTail = NULL;
while (scanf("%c", &val) != EOF)
{
if (val == '\n')
{
break;
}
buildBinaryTree(&treeRoot, &queHead, &queTail, val);
}
preOrder(treeRoot);
printf("\n------------------------\n");
midOrder(treeRoot);
printf("\n------------------------\n");
latOrder(treeRoot);
return 0;
}
十 一、C语言中常见的排序算法
1、冒泡排序
冒泡排序是笔者学到的第一个排序,时间复杂度为O(n^2),空间复杂度为O(1)。主要的思想在于,依次拿当前元素与后面的元素进行比较然后进行交换。算法中做了一个优化,定义一个flag,就是如果元素不再进行交换,说明数组元素有序,就停止循环。代码如下:
//冒泡排序
void bubble(int a[])
{
int flag;//是否有序的标记
for (int i = 0; i < N; i++) {
flag = 1;
for (int j = i + 1; j < N; j++) {
if (a[i] > a[j]) {
SWAP(a[i], a[j]);
flag = 0;
}
}
//如果函数中未发生交换,flag始终未1,那么数组有序,退出循环
if (flag) break;
}
}
2、选择排序
选择排序通过一轮一轮的比较得出每一轮中的最大或者最小值,再按顺序存储这些最值,最终可以得到一个有序序列,该算法的时间复杂度是O(n^2),空间复杂度为O(1)。代码如下:
//选择排序
void select(int a[])
{
int min_index;//最小值下标
for (int i = 0; i < N-1; i++) {
min_index = i;
for (int j = i + 1; j < N; j++) {
if (a[j] < a[min_index]) {
min_index = j;
}
}
//循环一轮后,得到本轮最小值,与a[i]进行交换
SWAP(a[min_index], a[i]);
}
}
3、插入排序
插入排序,其目的在于对未排序的序列元素,在前面有序的序列中进行扫描直到扫描出可以插入的位置,将其插入有序序列中。插入排序空间复杂度为O(n^2),空间复杂度为O(1)。代码实现如下:
//插入排序
void insert(int a[])
{
int insert_val;//即将插入的值
int j,i;
for (i = 1; i < N; i++) {
//记录插入元素
insert_val = a[i];
//遍历有序序列,查找可插入的位置
for (j = i - 1; j >= 0; j--) {
if (a[j] > insert_val) {
//元素后移,留出插入的位置
a[j + 1] = a[j];
}
//不大于此元素的时候则不用后移了,即找到了插入的位置,退出循环
else{
break;
}
}
//直接插入在后一个位置
a[j + 1] = insert_val;
}
}
4、希尔排序
希尔排序以插入排序为基础,设置了步长gap,希尔排序可以将组内的数据进行排序,相对于插入排序,待排序元素可以向前移动较多位置,插入排序则只能移动一位。相对于插入排序的效率,希尔排序要更高。希尔排序的时间复杂度为O(nlogn),看空间复杂度为O(1),具体代码如下:
void shell(int a[])
{
int insert_val, gap;
int i, j;
//设置步长,步长每次递减一半
for (gap = N / 2; gap > 0; gap--) {
//与插入排序类似,区别在于循环的增量为gap而不是1
for (i = gap; i < N; i++) {
insert_val = a[i];
//有序序列元素每次后移gap个位置
for (j = i - gap; j >= 0 && a[j] > insert_val; j -= gap) {
a[j + gap] = a[j];
}
a[j + gap] = insert_val;
}
}
}
5、快速排序(递归)
快速排序是非常常用的排序,主要是基于分治法的思想,设置一个基准值,基准值可以为数组中的任意元素,要求左侧元素都小于基准值,右侧元素都大于基准值,否则交换,然后以分界点再次递归,最后得到排好序的数组。虽然快速排序是不稳定排序,但是快速排序的效率很高,时间复杂度为O(nlogn),空间复杂度为O(logn)。声明:如下快速排序的代码参考AcWing算法基础班中给出的快速排序模板。代码如下:
//快速排序
void quick(int a[], int left, int right)
{
//递归出口,当最后两个元素或者一个元素有序退出
if (left >= right) return;
int x = a[(left + right) / 2];
int i = left - 1;
int j = right + 1;
while (i < j) {
//保证x左侧的元素都小于x
do i++; while (a[i] < x);
//保证x右侧的元素都大于x
do j--; while (a[j] > x);
if (i < j) SWAP(a[i], a[j]);
}
quick(a, left, j);
quick(a, j + 1, right);
}
6、堆排序
堆排序基于数组存储树的结构,这种特殊的结构叫做堆,近似于完全二叉树,其特性为子结点关键字大于或者小于父结点的关键字。
如果使用建大根堆或者小根堆的方式找出最大或最小的数会容易一些,时间复杂度为O(nlogn)。堆排序实际上就是找出当前序列中最大或者最小的数,然后将其放入尾部即树较低的位置,重复n次,故堆排序的时间复杂度为(nlogn),空间复杂度为O(1)。适用场景:十万个数中找出前10大的数。实现代码如下:
//调整某棵子树为大根堆
//堆得根从0下标开始,左孩子son = 2*dad+1
//堆得根从1下标开始,左孩子son = 2*dad
void adjustMaxHeap(int* a, int adjustPos, int len)
{
int dad = adjustPos;
int son = 2 * dad + 1;//左孩子下标
while (son < len) {//son要小于数组长度
//先比较左孩子和右孩子,谁大就和父亲比较
if (son + 1 < len && a[son + 1] > a[son]) {
son++;
}
//用大的孩子和父亲比较,比父亲大的要和父亲交换
if (a[son] > a[dad]) {
SWAP(a[son], a[dad]);
dad = son;
son = 2 * dad + 1;
}
//否则跳出循环,此父亲大于孩子
else {
break;
}
}
}
//堆排序
void heap(int a[])
{
int i;
//调整为大根堆
for (i = N / 2 - 1; i >= 0; i--) {
adjustMaxHeap(a, i, N);
}
//交换堆顶和尾部元素
SWAP(a[0], a[N - 1]);
for (i = N - 1; i > 1; i--) {
adjustMaxHeap(a, 0, i);//把剩下的元素调整为大根堆
SWAP(a[0], a[i - 1]);//把顶部元素和最后一个元素进行交换
}
}
7、归并排序
归并排序是二分法的典型案例,归并排序对其子序列,子序列再对子序列排序,保证其每个子序列有序,最终合并成有序序列。归并排序的时间复杂度为O(logn),空间复杂度为O(n)。实现代码如下,主要体会递归实现分治思想的奇妙之处:
//子序列归并
void merge_arr(int* a, int low, int mid, int high)
{
int b[N];
int i,j,k;
for(i = 0; i < N; i++) {
b[i] = a[i];
}
for (i = low, j = mid + 1, k = low; i <= mid && j <= high; k++) {
//两个序列进行比较,将较小的放入新序列中
if (b[j] < b[i]) {
a[k] = b[j];
j++;
}
else if (b[i] < b[j]) {
a[k] = b[i];
i++;
}
}
//判断两个序列是否为空,不为空则将剩余元素全部加入
while (i <= mid) {
a[k] = b[i];
k++;
i++;
}
while (j <= high) {
a[k] = b[j];
k++;
j++;
}
}
//归并排序
void merge(int a[], int low, int high)
{
if (low < high) {
int mid = (low + high) / 2;
merge(a, low, mid);
merge(a, mid + 1, high);
merge_arr(a, low, mid, high);
}
}
8、计数排序
计数排序类似于哈希表,相似之处在于,序列中待排序的数对应新开辟数组的下标,将对应下标的数组值+1,然后按照顺序将数值放回原数组中,即为有序的序列。这里值得考虑的是,如果待排序的序列中有较大的数则不宜选用计数排序,如{1,9999999},新开辟的数组空间会浪费很多。
计数排序的时间复杂度为O(n+k),空间复杂度为O(k)。
//计数排序
void count(int a[])
{
//M为元素的最大范围,这里M为100
int count[M] = { 0 };
int i, j, k;
//元素对应下标的值++
for (i = 0; i < N; i++) {
count[a[i]]++;
}
k = 0;
//将数填写回去
for (i = 0; i < M; i++) {
for (j = 0; j < count[i]; j++) {
a[k++] = i;
}
}
}
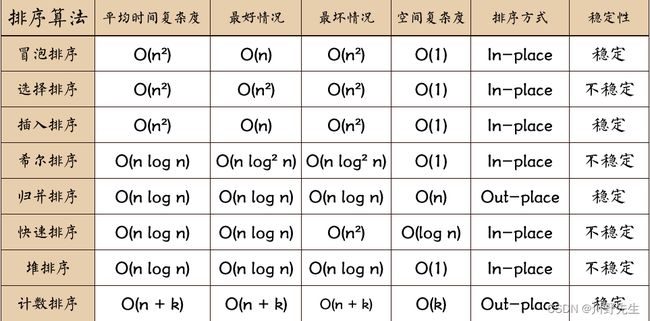
排序算法性能对比
十二、C语言中常见的查找算法
1、二分查找
二分查找是有序查找算法,先用查找值与中间值进行比较,在确定在左半边还是右半边继续查找。二分查找的时间复杂度为O(logn),还记得小时候玩过一个猜分数的游戏,现在想想如果用二分查找的方法去猜100分以内的分数最多7次就可以猜出来了。非递归代码如下:
#include2、哈希表
哈希表通过散列函数使得关键字key和表中位置建立一个相对位置。散列表:根据关键字直接进行访问的数据结构。散列函数最常见的是除数取余法,一般公式为f(key)=key mod p(p<=m),除此之外,还有直接定址法、数字分析法、平方取中法等。使用散列表是会出现多个key映射到同一位置的情况,这时候就需要处理冲突,一般使用线性探测法,除此之外还有平方探测法、再散列法、伪随机序列法、拉链法等。
下列代码中使用了除数取余法和线性再探测法,代码如下:
#include3、位图bitmap
位图用一个bit位来标记某个元素对应的value,而key即是这个元素。由于采用bit为单位来存储数据,因此在可以大大的节省存储空间。
一个32位整型,在内存中占32bit,可以用对应的32个bit位来表示十进制的0-31个数,bitmap算法利用这种思想处理大量数据的排序与查询,该算法重点在于如何建立十进制和二进制的映射关系。此外位图并非没有应用场景,在操作系统中对于磁盘的管理就是使用了位图,1和0表示磁盘块是否使用。这里给出代码:
参考博客:https://www.cnblogs.com/dyllove98/archive/2013/07/26/3217741.html
#include待续…
留言:实际上本文还有两个项目未实现,一个是红黑树,一个是编译器,作者先挖个坑,以后来填。欢迎佬们在评论区交流点赞。
红黑树补档
》》传送门在此《《