(二分、分治、贪心)北大暑期练习题
目录
01:派(二分——最大化最小值)
02:河中跳房子(二分——最大化最小值)
03:矩形分割(二分)
07:求排列的逆序数(分治)
08:输出前k大的数(分治)
4110:圣诞老人的礼物-Santa Clau’s Gifts(贪心)
4151:电影节(贪心)
POJ3190 Stall Reservations (贪心+优先队列)
01:派(二分——最大化最小值)
描述
我的生日要到了!根据习俗,我需要将一些派分给大家。我有N个不同口味、不同大小的派。有F个朋友会来参加我的派对,每个人会拿到一块派(必须一个派的一块,不能由几个派的小块拼成;可以是一整个派)。
我的朋友们都特别小气,如果有人拿到更大的一块,就会开始抱怨。因此所有人拿到的派是同样大小的(但不需要是同样形状的),虽然这样有些派会被浪费,但总比搞砸整个派对好。当然,我也要给自己留一块,而这一块也要和其他人的同样大小。
请问我们每个人拿到的派最大是多少?每个派都是一个高为1,半径不等的圆柱体。
输入
第一行包含两个正整数N和F,1 ≤ N, F ≤ 10 000,表示派的数量和朋友的数量。
第二行包含N个1到10000之间的整数,表示每个派的半径。
输出
输出每个人能得到的最大的派的体积,精确到小数点后三位。
样例输入
3 3
4 3 3样例输出
25.133
题解:最大化最小值问题。对于派的体积进行二分查找,判断是否满足条件(也就是假定一个解,并判定是否可行)。注意:有f+1个人共享派(包含主人),对于这种浮点数间的二分注意卡精度。
#include
#include
#include
#include
using namespace std;
#define PI acos(-1.0)
const int maxn=1e4+10;
double v[maxn],EPS=1e-6;
int n,f,a;
bool C(double x){
int cnt=0;
for(int i=0;i=f) return true;
return false;
}
void solve(){
sort(v,v+n);
double l=0,r=v[n-1],ans;
while(r-l>=EPS){
double mid=l+(r-l)/2;
if(C(mid)){
ans=mid;
l=mid;
}else r=mid;
}
printf("%.3lf\n",ans);
}
int main(){
scanf("%d%d",&n,&f);
f++;
for(int i=0;i 02:河中跳房子(二分——最大化最小值)
描述
每年奶牛们都要举办各种特殊版本的跳房子比赛,包括在河里从一个岩石跳到另一个岩石。这项激动人心的活动在一条长长的笔直河道中进行,在起点和离起点L远 (1 ≤ L≤ 1,000,000,000) 的终点处均有一个岩石。在起点和终点之间,有N (0 ≤ N ≤ 50,000) 个岩石,每个岩石与起点的距离分别为Di (0 < Di < L)。
在比赛过程中,奶牛轮流从起点出发,尝试到达终点,每一步只能从一个岩石跳到另一个岩石。当然,实力不济的奶牛是没有办法完成目标的。
农夫约翰为他的奶牛们感到自豪并且年年都观看了这项比赛。但随着时间的推移,看着其他农夫的胆小奶牛们在相距很近的岩石之间缓慢前行,他感到非常厌烦。他计划移走一些岩石,使得从起点到终点的过程中,最短的跳跃距离最长。他可以移走除起点和终点外的至多M (0 ≤ M ≤ N) 个岩石。
请帮助约翰确定移走这些岩石后,最长可能的最短跳跃距离是多少?
输入
第一行包含三个整数L, N, M,相邻两个整数之间用单个空格隔开。
接下来N行,每行一个整数,表示每个岩石与起点的距离。岩石按与起点距离从近到远给出,且不会有两个岩石出现在同一个位置。
输出
一个整数,最长可能的最短跳跃距离。
样例输入
25 5 2
2
11
14
17
21样例输出
4提示
在移除位于2和14的两个岩石之后,最短跳跃距离为4(从17到21或从21到25)。
题解:最大化最小值问题,本题可以说是P142 二分搜索——最大化最小值(POJ2456 Aggressive cows)的另一种表达方式。
#include
#include
#include
#include
using namespace std;
const int maxn=5e5+10;
int x[maxn],N,M,L;
bool C(int d){
int cnt=1,last=0;
for(int i=1;i<=N+1;i++){
if(x[i]-x[last]>=d){
cnt++;
last=i;
}
}
if(cnt>=N+2-M) return true;
return false;
}
void solve(){
int l=0,r=L,ans;
while(l<=r){
int mid=l+(r-l)/2;
if(C(mid)){
ans=mid;
l=mid+1;
}
else r=mid-1;
}
printf("%d\n",ans);
}
int main(){
scanf("%d%d%d",&L,&N,&M);
for(int i=1;i<=N;i++)
scanf("%d",&x[i]);
x[0]=0;
x[N+1]=L;
solve();
return 0;
}
七月二十六写的这题的代码如下:
//二分搜索:最大化最小值
#include
#include
#include
using namespace std;
const int maxn=5e4+10;
const int inf=1e9;
int L,N,M,D[maxn];
bool C(int d){
int last,crt;
for(int i=0;i1){
int mid=(lb+ub)/2;
if(C(mid)) lb=mid;
else ub=mid;
}
printf("%d\n",lb);
}
int main(){
scanf("%d%d%d",&L,&N,&M);
for(int i=0;i 03:矩形分割(二分)
描述
平面上有一个大矩形,其左下角坐标(0,0),右上角坐标(R,R)。大矩形内部包含一些小矩形,小矩形都平行于坐标轴且互不重叠。所有矩形的顶点都是整点。要求画一根平行于y轴的直线x=k(k是整数) ,使得这些小矩形落在直线左边的面积必须大于等于落在右边的面积,且两边面积之差最小。并且,要使得大矩形在直线左边的的面积尽可能大。注意:若直线穿过一个小矩形,将会把它切成两个部分,分属左右两侧。
输入
第一行是整数R,表示大矩形的右上角坐标是(R,R) (1 <= R <= 1,000,000)。
接下来的一行是整数N,表示一共有N个小矩形(0 < N <= 10000)。
再接下来有N 行。每行有4个整数,L,T, W 和 H, 表示有一个小矩形的左上角坐标是(L,T),宽度是W,高度是H (0<=L,T <= R, 0 < W,H <= R). 小矩形不会有位于大矩形之外的部分。
输出
输出整数n,表示答案应该是直线 x=n。 如果必要的话,x=R也可以是答案。
样例输入
1000 2 1 1 2 1 5 1 2 1
样例输出
5
#include
#include
using namespace std;
const int maxn=1e4+10;
typedef long long ll;
ll a[maxn];
struct Rectangle{
ll l,t,w,h;
ll s;
}rec[maxn];
ll r,n,mx;
ll C(ll x){
ll s1=0,s2=0;
for(int i=0;i=rec[i].l+rec[i].w) s1+=rec[i].s;
else if(x<=rec[i].l) s2+=rec[i].s;
else{
s1+=(x-rec[i].l)*rec[i].h;
s2+=(rec[i].l+rec[i].w-x)*rec[i].h;
}
}
return s1-s2;
}
void solve(){
ll lb=0,ub=r;
while(ub-lb>1){
//cout<0) ub=mid;
else lb=mid;
}
//cout< 07:求排列的逆序数(分治)
描述
在Internet上的搜索引擎经常需要对信息进行比较,比如可以通过某个人对一些事物的排名来估计他(或她)对各种不同信息的兴趣,从而实现个性化的服务。
对于不同的排名结果可以用逆序来评价它们之间的差异。考虑1,2,…,n的排列i1,i2,…,in,如果其中存在j,k,满足 j < k 且 ij > ik, 那么就称(ij,ik)是这个排列的一个逆序。
一个排列含有逆序的个数称为这个排列的逆序数。例如排列 263451 含有8个逆序(2,1),(6,3),(6,4),(6,5),(6,1),(3,1),(4,1),(5,1),因此该排列的逆序数就是8。显然,由1,2,…,n 构成的所有n!个排列中,最小的逆序数是0,对应的排列就是1,2,…,n;最大的逆序数是n(n-1)/2,对应的排列就是n,(n-1),…,2,1。逆序数越大的排列与原始排列的差异度就越大。
现给定1,2,…,n的一个排列,求它的逆序数。
输入
第一行是一个整数n,表示该排列有n个数(n <= 100000)。
第二行是n个不同的正整数,之间以空格隔开,表示该排列。
输出
输出该排列的逆序数。
样例输入
6
2 6 3 4 5 1样例输出
8提示
1. 利用二分归并排序算法(分治);
2. 注意结果可能超过int的范围,需要用long long存储。
来源
习题(15-4)
题解:分治。算法复杂度n*log(n),将序列平分成两块,左右两边都是有序的,比如说都是从小到大进行排列的,
2 5 7 9| 1 3 4 6 给左右两边分别设置一个指针,l1,l2.初始状态我们让l1指向2,l2指向1,可以看到2>1这就产生了1个逆序数。又因为l1所指向的数都比它后边的每一个数都要小,所以5 7 9 都能与1组成逆序数。
整个过程和归并排序很像,直接用归并排序代码附加一个计数即可。
代码1:
#include
#include
using namespace std;
const int maxn=1e5+10;
typedef long long ll;
int a[maxn],b[maxn],n;
ll sum;
void Merge(int v[],int l,int mid,int r,int tmp[]){
int p1=l,p2=mid+1,tg=0;
while(p1<=mid&&p2<=r){
if(v[p1]<=v[p2]){
tmp[tg++]=v[p1++];
}else{
sum+=(mid-p1+1); //注意点
tmp[tg++]=v[p2++];
}
}
while(p1<=mid)
tmp[tg++]=v[p1++];
while(p2<=r)
tmp[tg++]=v[p2++];
for(int i=0;i 当然,tmp数组也可不放在形参表里。
#include
#include
using namespace std;
const int maxn=1e5+10;
typedef long long ll;
int a[maxn],tmp[maxn],n;
ll sum;
void Merge(int v[],int l,int mid,int r){
int p1=l,p2=mid+1,tg=0;
while(p1<=mid&&p2<=r){
if(v[p1]<=v[p2]){
tmp[tg++]=v[p1++];
}else{
sum+=(mid-p1+1); 注意点
tmp[tg++]=v[p2++];
}
}
while(p1<=mid)
tmp[tg++]=v[p1++];
while(p2<=r)
tmp[tg++]=v[p2++];
for(int i=0;i 08:输出前k大的数(分治)
描述
给定一个数组,统计前k大的数并且把这k个数从大到小输出。
输入
第一行包含一个整数n,表示数组的大小。n < 100000。
第二行包含n个整数,表示数组的元素,整数之间以一个空格分开。每个整数的绝对值不超过100000000。
第三行包含一个整数k。k < n。
输出
从大到小输出前k大的数,每个数一行。
样例输入
10
4 5 6 9 8 7 1 2 3 0
5样例输出
9
8
7
6
5题解:1.排序后输出。时间复杂度为O(n*log(n));
2.分治:把前k大的数都弄到数组的右边。利用快排思想将前K大的数找出来,排序的时候只对只对k个数进行排序即可。快排思想分出k个数的时间复杂度为O(n),这k个数的排序的时间复杂度为O(n+k*log(k) ),所以总的时间复杂度为O(n+k*log(k) ).如果k比n小很多,那么时间复杂度接近O(n),这样会比方法1快很多。而如果n和k差不多大的时候,用分治来处理也就没什么意义了。
#include
#include
#include
#include
#include
using namespace std;
const int maxn=1e5+10;
int a[maxn],n,k;
void swp(int &a,int &b)
{
int temp=a;
a=b;
b=temp;
}
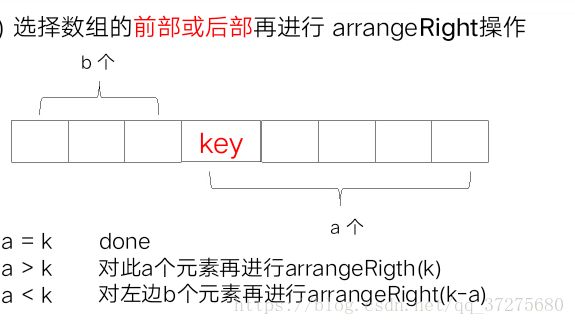
void arrangeRight(int v[],int l,int r,int k){ //把数组v[]区间[l,r]前k大的数都弄到数组的最右边
if(l>=r) return ;
int tmp=v[l];
int low=l,high=r;
while(low=tmp) high--;
swp(v[low],v[high]);
while(lowk) arrangeRight(v,low+1,r,k);
if(numn-k;i--)
printf("%d\n",a[i]);
return 0;
}
4110:圣诞老人的礼物-Santa Clau’s Gifts(贪心)
描述
圣诞节来临了,在城市A中圣诞老人准备分发糖果,现在有多箱不同的糖果,每箱糖果有自己的价值和重量,每箱糖果都可以拆分成任意散装组合带走。圣诞老人的驯鹿最多只能承受一定重量的糖果,请问圣诞老人最多能带走多大价值的糖果。
输入
第一行由两个部分组成,分别为糖果箱数正整数n(1 <= n <= 100),驯鹿能承受的最大重量正整数w(0 < w < 10000),两个数用空格隔开。其余n行每行对应一箱糖果,由两部分组成,分别为一箱糖果的价值正整数v和重量正整数w,中间用空格隔开。
输出
输出圣诞老人能带走的糖果的最大总价值,保留1位小数。输出为一行,以换行符结束。
样例输入
4 15
100 4
412 8
266 7
591 2样例输出
1193.0题解:贪心。重点关注下<运算符的重载。
#include
#include
#include
#include
using namespace std;
const double eps=1e-6;
struct Candy{
int v;int w;
bool operator < (const Candy &c)const{
return double(v)/w-double(c.v)/c.w>eps;
}
}candies[110];
int main(){
int n,w;
scanf("%d%d",&n,&w);
for(int i=0;i=candies[i].w){
ans+=candies[i].v;
w-=candies[i].w;
}else{
ans+=1.0*candies[i].v/candies[i].w*w;
w=0;
break;
}
}
printf("%.1lf\n",ans);
return 0;
} 4151:电影节(贪心)
描述
大学生电影节在北大举办! 这天,在北大各地放了多部电影,给定每部电影的放映时间区间,区间重叠的电影不可能同时看(端点可以重合),问李雷最多可以看多少部电影。
输入
多组数据。每组数据开头是n(n<=100),表示共n场电影。
接下来n行,每行两个整数(0到1000之间),表示一场电影的放映区间
n=0则数据结束
输出
对每组数据输出最多能看几部电影
样例输入
8
3 4
0 7
3 8
15 19
15 20
10 15
8 18
6 12
0
样例输出
3题解:贪心。
#include
#include
#include
#include
using namespace std;
struct Film{
int s;int e;
bool operator < (const Film &f)const{
if(e!=f.e) return ef.s;
}
}films[110];
int main(){
int n;
while(~scanf("%d",&n)&&n){
for(int i=0;i=films[last].e){
num++;
last=i;
}
}
printf("%d\n",num);
}
return 0;
} POJ3190 Stall Reservations (贪心+优先队列)
Description
Oh those picky N (1 <= N <= 50,000) cows! They are so picky that each one will only be milked over some precise time interval A..B (1 <= A <= B <= 1,000,000), which includes both times A and B. Obviously, FJ must create a reservation system to determine which stall each cow can be assigned for her milking time. Of course, no cow will share such a private moment with other cows.
Help FJ by determining:
- The minimum number of stalls required in the barn so that each cow can have her private milking period
- An assignment of cows to these stalls over time
Many answers are correct for each test dataset; a program will grade your answer.
Input
Line 1: A single integer, N
Lines 2..N+1: Line i+1 describes cow i's milking interval with two space-separated integers.
Output
Line 1: The minimum number of stalls the barn must have.
Lines 2..N+1: Line i+1 describes the stall to which cow i will be assigned for her milking period.
Sample Input
5
1 10
2 4
3 6
5 8
4 7Sample Output
4
1
2
3
2
4Hint
Explanation of the sample:
Here's a graphical schedule for this output:
Time 1 2 3 4 5 6 7 8 9 10
Stall 1 c1>>>>>>>>>>>>>>>>>>>>>>>>>>>
Stall 2 .. c2>>>>>> c4>>>>>>>>> .. ..
Stall 3 .. .. c3>>>>>>>>> .. .. .. ..
Stall 4 .. .. .. c5>>>>>>>>> .. .. ..Other outputs using the same number of stalls are possible.
题解:贪心,优先队列。
#include
#include
#include
#include
#include
using namespace std;
struct Cow{
int a,b;
int No;
bool operator<(const Cow &c)const{
return as.e;
}
Stall(int e1,int n):e(e1),No(n){}
};
int main(){
int n;
scanf("%d",&n);
for(int i=0;i pq;
for(int i=0;i