leetcode二叉树系列(一）

 

目录

1、对称二叉树

2、二叉树的层序遍历

 3、二叉树的最大深度

4、从前序和中序遍历构造二叉树 

1、对称二叉树

对称二叉树

题目描述：

 

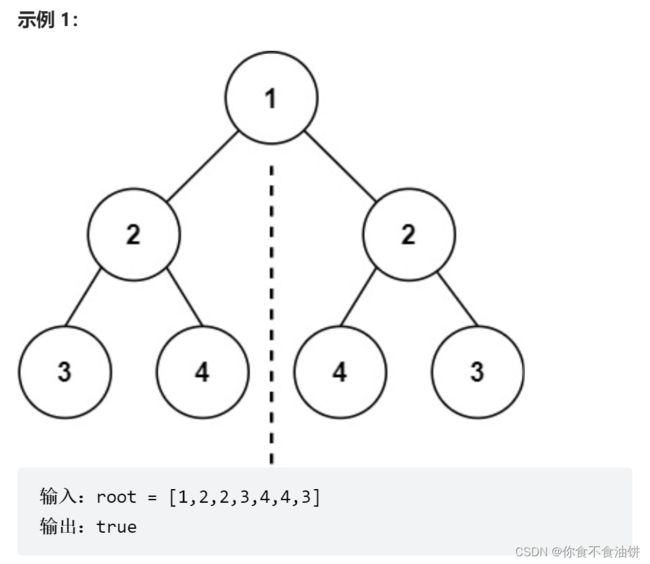
思路：要判断二叉树是否是对称二叉树，对称二叉树的条件大家得看清 是要root.left.right = root.right.left，我开始就吃了亏，没审清题，以为是要左节点等于左节点，右节点等于右节点；

这道题比较简单，我们直接进入代码：

    public boolean isSymmetric(TreeNode root) {    
        return dfs(root.left,root.right);
    }
    public boolean dfs(TreeNode left,TreeNode right){
        if(left == null && right == null) return true;
        if(left == null || right == null) return false;
        if( left.val != right.val) return false;

        return (dfs(left.left,right.right) && dfs(left.right,right.left));          
    }

2、二叉树的层序遍历

二叉树的层序遍历

题目描述：

 

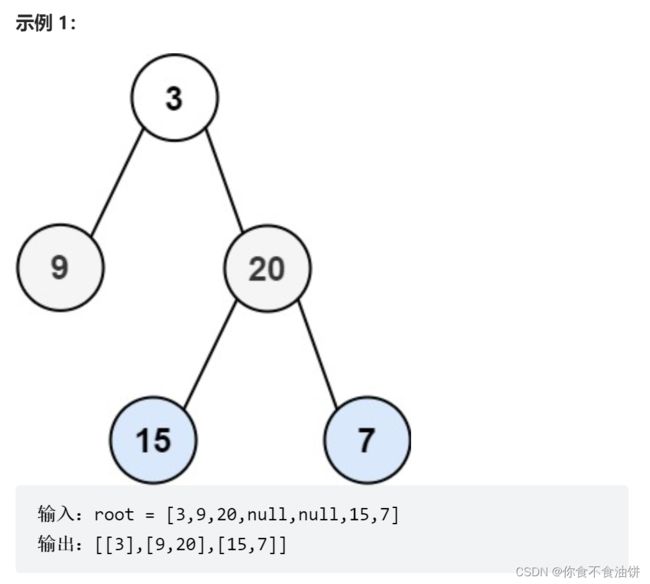
思路：层序遍历就是遍历二叉树时，从第一层依次遍历到第二层再到第三层，与我们往常的前序、中序、后序遍历不同；

BFS(广度优先遍历)，就是专门用于进行层序遍历的搜索算法，所以这道题我们会采用bfs来进行二叉树的层序遍历

代码如下：

public List> levelOrder(TreeNode root) {
    List> lists = new ArrayList<>();
    if (root == null) return lists;
    Queue queue = new LinkedList<>();
    queue.offer(root);
    while (!queue.isEmpty()){
        //size为每一层节点的个数
        int size = queue.size();
        List list = new ArrayList<>();
        for (int i = 0; i < size; i++) {
            TreeNode node = queue.poll();
            list.add(node.val);
            if (node.left != null) queue.offer(node.left);
            if (node.right != null) queue.offer(node.right);
        }
        lists.add(list);
    }
    return lists;
}

 3、二叉树的最大深度

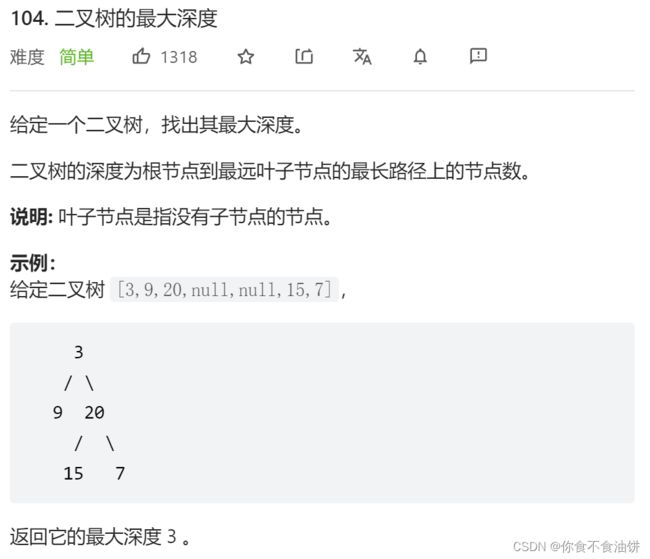
二叉树的最大深度

题目描述：

 

思路：就是做一个递归操作，很简单，直接看代码

    public int maxDepth(TreeNode root) {
        if(root == null) return 0;
        return Math.max(root.left == null ? 0 : maxDepth(root.left),
                        root.right == null ? 0 : maxDepth(root.right)) + 1;
    }

4、从前序和中序遍历构造二叉树 

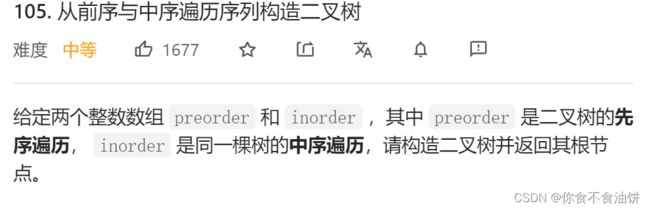
从前序和中序遍历构造二叉树

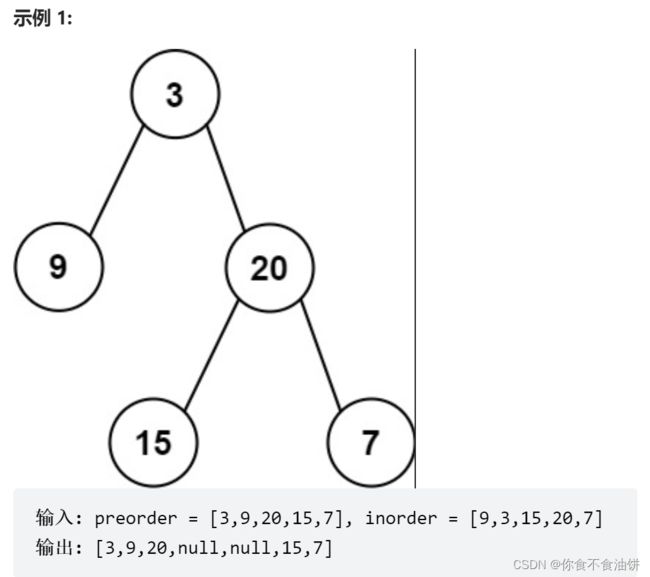
题目描述：

 

思路： 前序遍历数组[3,9,20,15,7],中序遍历数组[9,3,15,20,7]，进行递归操作

第一次递归，建立val为3的节点root，我们找到它在中序遍历数组中出现的位置，

root.left =[9]，root.right = [20,15,7]

第二次递归，建立val为9的节点root，此时回退，返回root；

第三次递归，建立val为20的节点root，我们依然找到它在中序遍历数组出现的位置，

root.left = [15]，root.right = [7]

第四次递归，建立val为15的节点root，此时回退，返回root；

第五次递归，建立val为7的节点root，此时回退，返回root；

第五次递归结束时，此时回退完成后，二叉树就已经建立完毕

至于我们判断回退的条件，我们可以递归参数中加入preStart、preEnd表示在前序数组中的开始索引位置和结束索引位置，当preStart == preEnd时，退出此次递归；

进入代码：

public TreeNode buildTree(int[] preorder, int[] inorder) {
    LinkedHashMap map = new LinkedHashMap<>();
    return build(preorder,0,preorder.length,inorder,0,inorder.length);
}
public TreeNode build(int[] preorder,int preStart,int preEnd,int[] inorder,int inStart,int inEnd){
    if(preStart == preEnd) return null;
    int rootVal = preorder[preStart];
    //每一个节点都是他子节点的主节点
    TreeNode root = new TreeNode(rootVal);
    int index = inStart;
    for(;index < inEnd;index++){
        if(rootVal == inorder[index])
            break;
    }
    //移动了多少个位置才到达主节点
    int leftnum = index - inStart;
    root.left = build(preorder,preStart+1,preStart+leftnum+1,inorder,inStart,index);
    root.right = build(preorder,preStart+leftnum+1,preEnd,inorder,index+1,inEnd);
    return root;
}

持续更新中~~