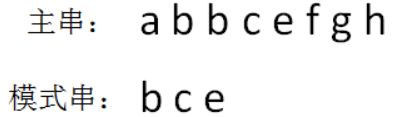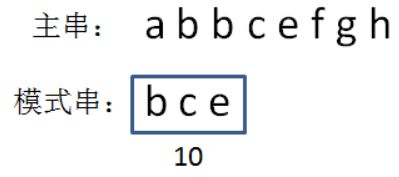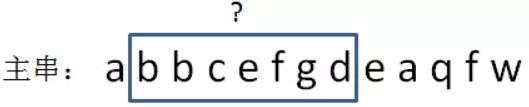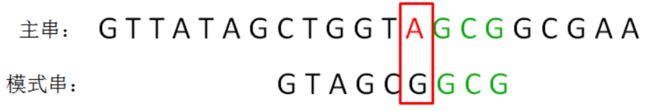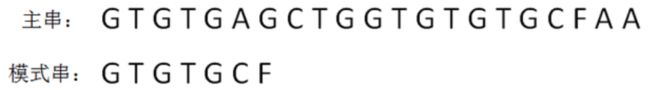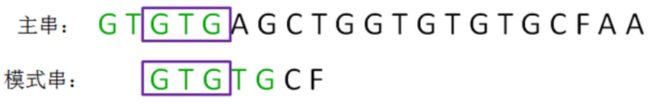字符串匹配算法
目录
1 字符串匹配问题的形式定义
2 BF(Brute Force,暴力检索)
2.1 步骤
2.2 复杂度分析
2.3 Python实现
3 RK(Robin-Karp,哈希检索)
3.1 RK算法的具体工作过程
3.1.1 第一步,生成模式串的hashcode
3.1.2 生成主串当中第一个等长子串的hashcode
3.1.3 第三步,比较两个hashcode。
3.1.4 第四步,生成主串当中第二个等长子串的hashcode。
3.1.5 第五步,比较两个hashcode
3.1.6 第六步,生成主串当中第三个等长子串的hashcode
3.1.7 第七步,比较两个hashcode
3.1.8 第八步,逐个字符比较两字符串
3.2 hash的计算优化
3.3 时间复杂度
3.4 Python 实现
4 Boyer- Moore算法
4.1 坏字符规则
4.2 好后缀规则
4.3 移动规则
4.4 Python实现
4.4.1 计算坏字符bmBc
4.4.2 计算好后缀数组bmGs[]
4.4.3 bmGc数组的辅助数组suff[]
4.4.4 示例
5 KMP
5.1 整体思路
5.2 求next数组
5.2.1 next数组是什么?
5.2.2 如何寻找前后缀,生成next
5.2.3 如何生成next数组
5.3 KMP实现
字符串匹配算法,是在实际工程中经常遇到的问题,也是各大公司笔试面试的常考题目。此算法通常输入为原字符串(string)和子串(pattern),要求返回子串在原字符串中首次出现的位置。比如原字符串为“ABCDEFG”,子串为“DEF”,则算法返回3。常见的算法包括:BF(Brute Force,暴力检索)、RK(Robin-Karp,哈希检索)、KMP(教科书上最常见算法)、BM(Boyer Moore)、Sunday等。
1 字符串匹配问题的形式定义
- 文本(Text)是一个长度为 n 的数组 T[1..n];
- 模式(Pattern)是一个长度为 m 且 m≤n 的数组 P[1..m];
- T 和 P 中的元素都属于有限的字母表 Σ 表;
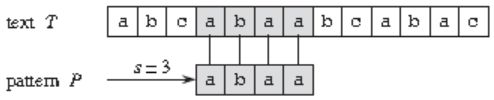
- 如果 0≤s≤n-m,并且 T[s+1..s+m] = P[1..m],即对 1≤j≤m,有 T[s+j] = P[j],则说模式 P 在文本 T 中出现且位移为 s,且称 s 是一个有效位移(Valid Shift)。
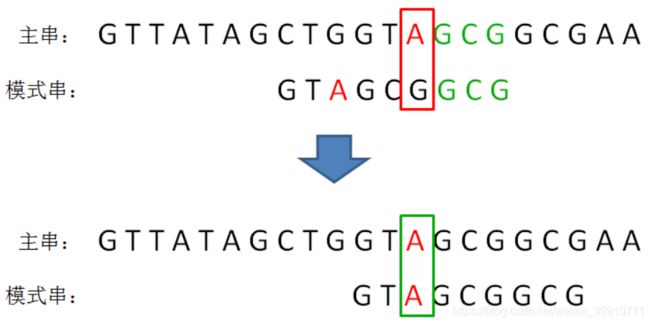
比如上图中,目标是找出所有在文本 T = abcabaabcabac 中模式 P = abaa 的第一次出现。该模式在此文本中仅出现一次,即在位移 s = 3 处,位移 s = 3 是有效位移。
2 BF(Brute Force,暴力检索)
2.1 步骤
我们可以让字符串 needle 与字符串 haystack 的所有长度为 m 的子串均匹配一次。
为了减少不必要的匹配,我们每次匹配失败即立刻停止当前子串的匹配,对下一个子串继续匹配。如果当前子串匹配成功,我们返回当前子串的开始位置即可。如果所有子串都匹配失败,则返回 −1。
2.2 复杂度分析
- 时间复杂度:O(n×m),其中 n 是字符串 haystack 的长度,m 是字符串 needle 的长度。最坏情况下我们需要将字符串needle 与字符串haystack 的所有长度为 m 的子串均匹配一次。
- 空间复杂度:O(1)。我们只需要常数的空间保存若干变量。
2.3 Python实现
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
if not haystack:
return -1
if not needle:
return 0
len_haystack = len(haystack)
len_needle = len(needle)
i = 0
j = 0
start = 0
while start <= len_haystack - len_needle:
if haystack[i] == needle[j]:
i += 1
j += 1
else:
start += 1
i = start
j = 0
if j == len_needle:
return start
return -1
s = Solution()
print(s.strStr("aabcaaabcbacd", "aabcb"))
print(s.strStr("hello", "llo"))
print(s.strStr("hello", "lle"))
3 RK(Robin-Karp,哈希检索)
Rabin-Karp算法是由Rabin和Karp提出的一个在实际中有比较好应用的字符串匹配算法,此算法的预处理时间为O(m),但它的在最坏情况下的时间复杂度为O((2n-m+1)m),而平均复杂度接近O(m+n),此算法的主要思想就是通过对字符串进行哈稀运算,使得算法可以容易的排除大量的不相同的字符串。
假设模式字符串的长度为m,利用Horner法则p = p[m] + 10(p[m -1] + 10(p[m-2]+...+10(p[2]+10p[1])...)),求出模式字符串的哈希值p,而对于文本字符串来说,对应于每个长度为m的子串的哈稀值为t(s+1)=10(t(s)-10^(m-1)T[s+1])+T[s+m+1],然后比较此哈稀值与模式字符串的哈稀值是否相等,若不相同,则字符串一定不同,若相同,则需要进一步的按位比较,所以它的最坏情况下的时间复杂度为O(mn)。
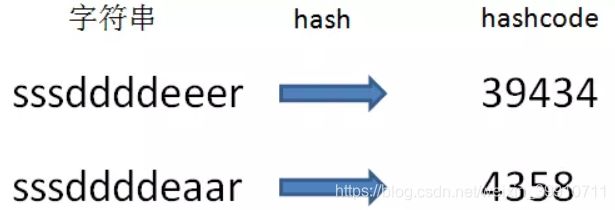
用过哈希表的朋友们都知道,每一个字符串都可以通过某种哈希算法,转换成一个整型数,这个整型数就是hashcode:
hashcode = hash(string)显然,相对于逐个字符比较两个字符串,仅比较两个字符串的hashcode要容易得多。
3.1 RK算法的具体工作过程
给定主串和模式串如下(假定字符串只包含26个小写字母):
3.1.1 第一步,生成模式串的hashcode
生成hashcode的算法多种多样,比如:
(1)按位相加
这是最简单的方法,我们可以把a当做1,b当做2,c当做3......然后把字符串的所有字符相加,相加结果就是它的hashcode。
bce = 2 + 3 + 5 = 10但是,这个算法虽然简单,却很可能产生hash冲突,比如bce、bec、cbe的hashcode是一样的。
(2)转换成26进制数
既然字符串只包含26个小写字母,那么我们可以把每一个字符串当成一个26进制数来计算。
bce = 2*(26^2) + 3*26 + 5 = 1435这样做的好处是大幅减少了hash冲突,缺点是计算量较大,而且有可能出现超出整型范围的情况,需要对计算结果进行取模。
为了方便演示,后续我们采用的是按位相加的hash算法,所以bce的hashcode是10:
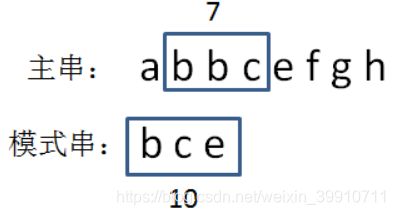
3.1.2 生成主串当中第一个等长子串的hashcode
由于主串通常要长于模式串,把整个主串转化成hashcode是没有意义的,只有比较主串当中和模式串等长的子串才有意义。
因此,我们首先生成主串中第一个和模式串等长的子串hashcode,
即abb = 1 + 2 + 2 = 5:
3.1.3 第三步,比较两个hashcode。
显然,5!=10,说明模式串和第一个子串不匹配,我们继续下一轮比较。
3.1.4 第四步,生成主串当中第二个等长子串的hashcode。
bbc = 2 + 2 + 3 = 7:
3.1.5 第五步,比较两个hashcode
显然,7!=10,说明模式串和第二个子串不匹配,我们继续下一轮比较。
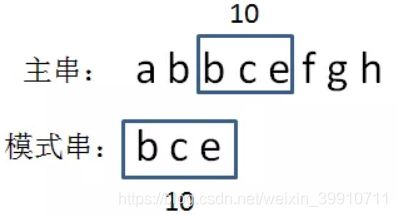
3.1.6 第六步,生成主串当中第三个等长子串的hashcode
bce= 2 + 3 + 5 = 10:
3.1.7 第七步,比较两个hashcode
显然,10 ==10,两个hash值相等!这是否说明两个字符串也相等呢?
别高兴的太早,由于存在hash冲突的可能,我们还需要进一步验证。
3.1.8 第八步,逐个字符比较两字符串
hashcode的比较只是初步验证,之后我们还需要像BF算法那样,对两个字符串逐个字符比较,最终判断出两个字符串匹配。
最后得出结论,模式串bce是主串abbcefgh的子串,第一次出现的下标是2。
3.2 hash的计算优化
每次hash的时间复杂度是o(n),如果把全部子串都进行hash,总的时间复杂度和BF算法一样,是o(mn)。因此需要对hash的计算方法进行优化:对子串的hash计算并不是独立的,从第二个子串开始,每一个子串的hash都可以由上一个子串的简单增量计算来得到:
让我们再来看一个例子:
![]()
上图中,我已知子串abbcefg的hashcode是26,那么如何计算下一个子串,也就是bbcefgd的hashcode呢?
我们没有必要把子串的字符重新进行累加运算,而是可以采用一个更简单的方法。由于新子串的前面少了一个a,后面多了一个d,所以:
再下一个子串bcefgde的计算也是同理:
3.3 时间复杂度
RK算法计算单个子串hash的时间复杂度是o(n),但由于后续子串hash是增量计算,所以总的时间复杂度仍然是o(n)。
RK算法的缺点在于哈希冲突,每一次哈希冲突的时候,RK算法都要对子串和模式串进行逐个字符的比较,如果冲突太多了,RK算法就退化成了BF算法。
3.4 Python 实现
import string
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
def get_hash_value(str_hash, hash_table):
hash_value = 0
for word in str_hash:
hash_value = hash_value + hash_table[word]
return hash_value
hash_table = {}
i = 1
for word in string.ascii_lowercase:
hash_table[word] = i
i += 1
if not haystack:
return -1
if not needle:
return 0
len_haystack = len(haystack)
len_needle = len(needle)
needle_hash = get_hash_value(needle, hash_table)
haystack_hash = get_hash_value(haystack[:len_needle], hash_table)
i = 0
j = 0
while i <= len_haystack - len_needle:
if haystack_hash != needle_hash:
if len_haystack - i == len_needle:
return -1
haystack_hash = haystack_hash - hash_table[haystack[i]] + hash_table[haystack[i + len_needle]]
i += 1
else:
while j < len_needle:
if haystack[i + j] != needle[j]:
haystack_hash = haystack_hash - hash_table[
haystack[i]] + hash_table[haystack[i + len_needle]]
i += 1
break
else:
j += 1
if j == len_needle:
return i
return -1
s = Solution()
print(s.strStr("aabcaaabcbacd", "aabcb"))
print(s.strStr("hello", "llo"))
print(s.strStr("hello", "lle"))4 Boyer- Moore算法
在用于查找子字符串的算法当中,BM(Boyer-Moore)算法被认为最高效的字符串搜索算法,它由Bob Boyer和J Strother Moore设计于1977年。 一般情况下,比KMP算法快3-5倍。该算法常用于文本编辑器中的搜索匹配功能,比如大家所熟知的GNU grep命令使用的就是该算法,这也是GNU grep比BSD grep快的一个重要原因。
BF算法在比较过程中有很多是没有意义的,但是BF算法还是让模式串一位一位挪动;RK算法回避了字符的直接比较,改为比较两个字符串的哈希值,但这样做可能产生哈希冲突,性能并不稳定。那么,能否仍然采用字符比较的思路,并且尽量减少无谓的比较呢?这就是BM算法的比较方向。
BM算法的精华就在于BM(text, pattern),也就是BM算法当不匹配的时候一次性可以跳过不止一个字符。即它不需要对被搜索的字符串中的字符进行逐一比较,而会跳过其中某些部分。通常搜索关键字越长,算法速度越快。它的效率来自于这样的事实:对于每一次失败的匹配尝试,算法都能够使用这些信息来排除尽可能多的无法匹配的位置。即它充分利用待搜索字符串的一些特征,加快了搜索的步骤。
BM算法制定了两条规则,一个是“坏字符规则”,一个是“好后缀规则”。BM算法实际上包含两个并行的算法(也就是两个启发策略):坏字符算法(bad-character shift)和好后缀算法(good-suffix shift)。这两种算法的目的就是让模式串每次向右移动尽可能大的距离。
4.1 坏字符规则
“坏字符” 是什么意思?就是指模式串和子串当中不匹配的字符。
(1)第一轮
还以上面的字符串为例,当模式串和主串的第一个等长子串比较时,子串的最后一个字符T就是坏字符:
坏字符不是主串位置2的字符T,是因为BM的检测顺序是相反的,是从字符串的最右侧向最左侧检测的。
当检测到第一个坏字符之后,我们有必要让模式串一位一位向后挪动和比较吗?并不需要。
因为只有模式串与坏字符T对齐的位置也是字符T的情况下,两者才有匹配的可能。
(2)第二轮
不难发现,模式串的第1位字符也是T,这样一来我们就可以对模式串做一次“乾坤大挪移”,直接把模式串当中的字符T和主串的坏字符对齐,进行下一轮的比较:
坏字符的位置越靠右,下一轮模式串的挪动跨度就可能越长,节省的比较次数也就越多。这就是BM算法从右向左检测的好处。
接下来,我们继续逐个字符比较,发现右侧的G、C、G都是一致的,但主串当中的字符A,是又一个坏字符:
(3)第三轮
我们按照刚才的方式,找到模式串的第2位字符也是A,于是我们把模式串的字符A和主串中的坏字符对齐,进行下一轮比较:
接下来,我们继续逐个字符比较,这次发现全部字符都是匹配的,比较完成:
上述使用3轮就比较完成了。如果坏字符在模式串中不存在,就直接把模式串挪到主串坏字符的下一位:
总结:
当出现一个坏字符时, BM算法向右移动模式串, 让模式串中最靠右的对应字符与坏字符相对,然后继续匹配。坏字符算法有两种情况。
Case1:模式串中有对应的坏字符时,让模式串中最靠右的对应字符与坏字符相对(PS:BM不可能走回头路,因为若是回头路,则移动距离就是负数了,肯定不是最大移动步数了),如下图。
Case2:模式串中不存在坏字符,很好,直接右移整个模式串长度这么大步数,如下图。
But, 如果遇到下面这样的情况,
开始 pattern中的c 和 text中的b 不匹配,按上面的规则将pattern右移直至最右边的b与text的b对齐进行比对。再将 pattern中的c 与 text中的c 进行比对,匹配继续往左比对,直到位置3处pattern中的a与text中的b不匹配了,按上面讲的启发式规则应该将pattern中最右边的b与text的b对齐,可这时发现啥了?pattern走了回头路,干吗?当然不干,才不要那么傻,针对这种情况,只需要将pattern简单的右移一步即可,坚持不走回头路!
4.2 好后缀规则
“好后缀” 又是什么意思?就是指模式串和子串当中相匹配的后缀。
让我们看一组新的例子:
对于上面的例子,如何我们继续使用“坏字符规则”,会有怎样的效果呢?
从后向前比对字符,我们发现后面三个字符都是匹配的,到了第四个字符的时候,发现坏字符G:
接下来我们在模式串找到了对应的字符G,但是按照坏字符规则,模式串仅仅能够向后挪动一位:
这时候坏字符规则显然并没有起到作用,为了能真正减少比较次数,轮到我们的好后缀规则出场了。由于好后缀规则的实现细节比坏字符规则要难理解得多,所以我们这里只介绍一个大概思路:
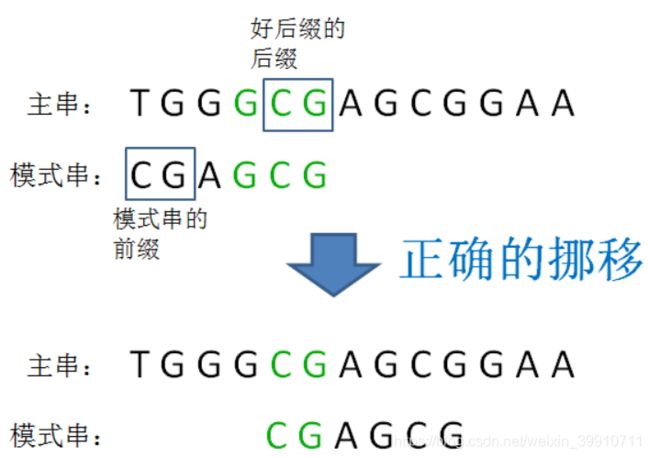
我们回到第一轮的比较过程,发现主串和模式串都有共同的后缀“GCG”,这就是所谓的“好后缀”。
如果模式串其他位置也包含与“GCG”相同的片段,那么我们就可以挪动模式串,让这个片段和好后缀对齐,进行下一轮的比较:
显然,在这个例子中,采用好后缀规则能够让模式串向后移动更多位,节省了更多无谓的比较。
如果模式串汇中不存在其他与好后缀相同的片段,不能直接挪动模式串到好后缀的后面,如下:
要先判断一种特殊情况:模式串的前缀是否和好后缀的后缀相匹配,免得挪过头了。
总结:
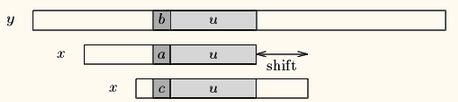
如果程序匹配了一个好后缀, 并且在模式中还有另外一个相同的后缀或后缀的部分, 那把下一个后缀或部分移动到当前后缀位置。假如说,pattern的后u个字符和text都已经匹配了,但是接下来的一个字符不匹配,我需要移动才能匹配。如果说后u个字符在pattern其他位置也出现过或部分出现,我们将pattern右移到前面的u个字符或部分和最后的u个字符或部分相同,如果说后u个字符在pattern其他位置完全没有出现,很好,直接右移整个pattern。这样,好后缀算法有三种情况,如下图所示:
- Case1:模式串中有子串和好后缀完全匹配,则将最靠右的那个子串移动到好后缀的位置继续进行匹配。
- Case2:如果不存在和好后缀完全匹配的子串,则在好后缀中找到具有如下特征的最长子串,使得P[m-s…m]=P[0…s]。
- Case3:如果完全不存在和好后缀匹配的子串,则右移整个模式串。
4.3 移动规则
BM算法的移动规则是:
j += MAX(shift(好后缀),shift(坏字符)),即BM算法是每次向右移动模式串的距离是,按照好后缀算法和坏字符算法计算得到的最大值。shift(好后缀)和shift(坏字符)通过模式串的预处理数组的简单计算得到。坏字符算法的预处理数组是bmBc[],好后缀算法的预处理数组是bmGs[]。
什么时候使用“坏字符规则”,什么时候使用“好后缀规则”?可以在每一轮的字符比较之后,按照坏字符和好后缀规则分别相应的挪动距离,哪一种距离更长,就把模式串挪到相应的长度。
4.4 Python实现
BM算法子串比较失配时,按坏字符算法计算pattern需要右移的距离,要借助bmbc数组,而按好后缀算法计算pattern右移的距离则要借助bmgs数组。
"坏字符规则":
后移位数 = 坏字符的位置 - 搜索词中的上一次出现位置
"好后缀规则":
后移位数 = 好后缀的位置 - 搜索词中的上一次出现位置
举例来说,如果字符串"ABCDAB"的后一个"AB"是"好后缀"。那么它的位置是5(从0开始计算,取最后的"B"的值),在"搜索词中的上一次出现位置"是1(第一个"B"的位置),所以后移 5 - 1 = 4位,前一个"AB"移到后一个"AB"的位置。
再举一个例子,如果字符串"ABCDEF"的"EF"是好后缀,则"EF"的位置是5 ,上一次出现的位置是 -1(即未出现),所以后移 5 - (-1) = 6位,即整个字符串移到"F"的后一位。
这个规则有三个注意点:
(1)"好后缀"的位置以最后一个字符为准。假定"ABCDEF"的"EF"是好后缀,则它的位置以"F"为准,即5(从0开始计算)。
(2)如果"好后缀"在搜索词中只出现一次,则它的上一次出现位置为 -1。比如,"EF"在"ABCDEF"之中只出现一次,则它的上一次出现位置为-1(即未出现)。
(3)如果"好后缀"有多个,则除了最长的那个"好后缀",其他"好后缀"的上一次出现位置必须在头部。比如,假定"BABCDAB"的"好后缀"是"DAB"、"AB"、"B",请问这时"好后缀"的上一次出现位置是什么?回答是,此时采用的好后缀是"B",它的上一次出现位置是头部,即第0位。这个规则也可以这样表达:如果最长的那个"好后缀"只出现一次,则可以把搜索词改写成如下形式进行位置计算"(DA)BABCDAB",即虚拟加入最前面的"DA"。
4.4.1 计算坏字符bmBc
因为 i 位置处的字符可能在pattern中多处出现(如下图所示),而我们需要的是最右边的位置。
如前所述,bmBc[]的计算分两种情况,与前一一对应。
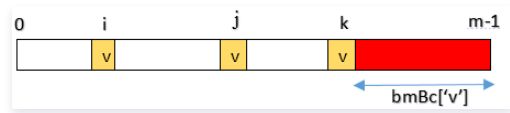
- Case1:字符在模式串中有出现,bmBc[‘v’]表示字符v在模式串中最后一次出现的位置,距离模式串串尾的长度,如上图所示。
- Case2:字符在模式串中没有出现,如模式串中没有字符v,则BmBc[‘v’] = strlen(pattern)。
注:pattern中的最后一个字符,如果没有在前面出现过,那么它的bmBc值为m;如果出现过,按照出现的倒数第二个计算。
写成代码也非常简单:
def get_bmbc(needle):
bmbc = {}
m = len(needle)
for i in range(m-1):
bmbc[needle[i]] = m-1-i
if needle[-1] not in bmbc.keys():
bmbc[needle[-1]] = m
return bmbc计算pattern需要右移的距离,要借助bmBc数组,那么bmBc的值是不是就是pattern实际要右移的距离呢?No,想想也不是,比如前面举例说到利用bmBc算法还可能走回头路,也就是右移的距离是负数,而bmBc的值绝对不可能是负数,所以两者不相等。那么pattern实际右移的距离怎么算呢?这个就要看text中坏字符的位置了,前面说过坏字符算法是针对text的,还是看图吧,一目了然。图中v是text中的坏字符(对应位置i+j),在pattern中对应不匹配的位置为i,那么pattern实际要右移的距离就是:bmbc[‘v’] – (m - 1 - i)。
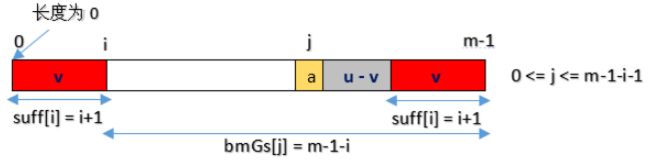
4.4.2 计算好后缀数组bmGs[]
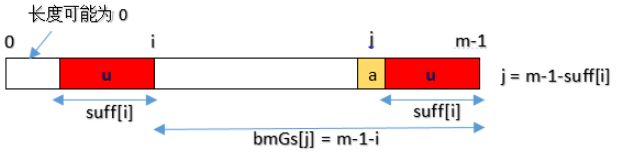
这里bmGs[]的下标是数字而不是字符了,表示字符在pattern中位置。
如前所述,bmGs数组的计算分三种情况,与前一一对应。假设图中好后缀长度用数组suff[]表示。
- Case1:对应好后缀算法case1,如下图,j是好后缀之前的那个位置。
- Case2:对应好后缀算法case2:如下图所示:
- Case3:对应与好后缀算法case3,bmGs[i] = strlen(pattern)= m
代码如下:
def get_bmgs(needle):
m = len(needle)
suff = get_suff_2(needle)
print("suff: ", suff)
# Case3, 先全部赋值为m
bmgs = [m] * m
# case 2
j = 0
i = m - 1
while i >= 0:
# 当0-i的值与结尾的i+1个值相等时
if suff[i] == i+1:
# j = i
# 0到 m-1-i 的值改为 m-i-1
while j < m-1-i:
if bmgs[j] == m:
bmgs[j] = m-i-1
j += 1
i -= 1
# Case1
i = 0
while i <= m-2:
bmgs[m-1-suff[i]] = m-1-i
i += 1
return bmgs4.4.3 bmGc数组的辅助数组suff[]
在计算bmGc数组时,为提高效率,先计算辅助数组suff[]表示好后缀的长度。实际上 suff[i] 就是求pattern中以 i 位置字符为后缀和以最后一个字符为后缀的公共后缀串的长度。
举个例子:
- i : 0 1 2 3 4 5 6 7
- pattern: b c a b a b a b
计算suff[i]:
- 当i=7时,按定义suff[7] = strlen(pattern) = 8
- 当i=6时,以pattern[6]为后缀的后缀串为bcababa,以最后一个字符b为后缀的后缀串为bcababab,两者没有公共后缀串,所以suff[6] = 0
- 当i=5时,以pattern[5]为后缀的后缀串为bcabab,以最后一个字符b为后缀的后缀串为bcababab,两者的公共后缀串为abab,所以suff[5] = 4
- 以此类推……
- 当i=0时,以pattern[0]为后缀的后缀串为b,以最后一个字符b为后缀的后缀串为bcababab,两者的公共后缀串为b,所以suff[0] = 1
代码如下:
def get_suff(needle):
start_time = time.time()
len_needle = len(needle)
suff = [len_needle] * len_needle
for i in range(len_needle-2, -1, -1):
j = i
while j >= 0 and needle[j] == needle[len_needle-1-(i-j)]:
j -= 1
suff[i] = i - j
print(time.time() - start_time)
return suff优化:
上述常规方法太暴力了,对其进行改进。基本的扫描都是从右向左,改进的地方就是利用了已经计算得到的suff[]值,计算现在正在计算的suff[]值。具体怎么利用,看下图:
- i 是当前正准备计算suff[]值的那个位置。
- f 是上一个成功进行匹配的起始位置(不是每个位置都能进行成功匹配的, 实际上能够进行成功匹配的位置并不多)。
- g 是上一次进行成功匹配的失配位置。
如果i在g和f之间,那么一定有P[i]=P[m-1-f+i],即两个字符相同;并且如果suff[m-1-f+i] < i-g, 则suff[i] = suff[m-1-f+i],这不就利用了前面的suff了吗。
PS:这里有些人可能觉得应该是suff[m-1-f+i] <= i – g,因为若suff[m-1-f+i] = i – g,还是没超过suff[f]的范围,依然可以利用前面的suff[],但这是错误的,比如一个极端的例子:
- i : 0 1 2 3 4 5 6 7 8 9
- pattern: a a a a a b a a a a
suff[4] = 4,这里 f=4,g=0,当 i=3时,这时suff[m-1=f+i]=suff[8]=3,而suff[3]=4,两者不相等,因为上一次的失配位置g可能会在这次得到匹配。
代码如下:
def get_suff_2(needle):
start_time = time.time()
m = len(needle)
suff = [m] * m
f = m-1
g = 0
for i in range(m - 2, -1, -1):
if f != m-1 and suff[m-1-(f-i)] < i-g and i > g:
suff[i] = suff[m-1-(f-i)]
else:
j = i
while j >= 0 and needle[j] == needle[m-1-(i-j)]:
j -= 1
suff[i] = i - j
if i != j:
f = i
g = j
print(time.time() - start_time)
return suff4.4.4 示例
text:abcddgbsbcabababerzbdj
pattern:bcababab
bmBc[]、suff[]和bmGs[]结果如下:
PS:这里也许有人会问:bmBc[‘b’]怎么等于2,它最后出现在pattern最后一个位置,如果按照最后一个位置计算,就是原地不动或走回头路。因此需要使用它出现的倒数第二个位置。
代码如下:
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
import time
class Solution:
def strStr(self, haystack, needle):
def get_suff(needle):
start_time = time.time()
len_needle = len(needle)
suff = [len_needle] * len_needle
for i in range(len_needle-2, -1, -1):
j = i
while j >= 0 and needle[j] == needle[len_needle-1-(i-j)]:
j -= 1
suff[i] = i - j
print(time.time() - start_time)
return suff
def get_suff_2(needle):
start_time = time.time()
m = len(needle)
suff = [m] * m
f = m-1
g = 0
for i in range(m - 2, -1, -1):
if f != m-1 and suff[m-1-(f-i)] < i-g and i > g:
suff[i] = suff[m-1-(f-i)]
else:
j = i
while j >= 0 and needle[j] == needle[m-1-(i-j)]:
j -= 1
suff[i] = i - j
if i != j:
f = i
g = j
print(time.time() - start_time)
return suff
def get_bmbc(needle):
bmbc = {}
m = len(needle)
for i in range(m-1):
bmbc[needle[i]] = m-1-i
if needle[-1] not in bmbc.keys():
bmbc[needle[-1]] = m
return bmbc
def get_bmgs(needle):
m = len(needle)
suff = get_suff_2(needle)
print("suff: ", suff)
# Case3, 先全部赋值为m
bmgs = [m] * m
# case 2
j = 0
i = m - 1
while i >= 0:
# 当0-i的值与结尾的i+1个值相等时
if suff[i] == i+1:
# j = i
# 0到 m-1-i 的值改为 m-i-1
while j < m-1-i:
if bmgs[j] == m:
bmgs[j] = m-i-1
j += 1
i -= 1
# Case1
i = 0
while i <= m-2:
bmgs[m-1-suff[i]] = m-1-i
i += 1
return bmgs
# 获取坏字符
bmbc = get_bmbc(needle)
print(bmbc)
# 获取好后缀数组
bmgs = get_bmgs(needle)
print(bmgs)
# 进行比较
m = len(needle)
n = len(haystack)
i = m - 1
j = 0
while j <= n-m:
while i >= 0 and needle[i] == haystack[i+j]:
i -= 1
if i < 0:
print("Find it, the position is %d: ", j)
return j
else:
bmbc_j = m if haystack[i + j] not in bmbc.keys() else bmbc[haystack[i + j]]
j += max(bmbc_j - m + 1 + i, bmgs[i])
i = m-1
print("No find.\n")
return -1
s = Solution()
print(s.strStr("aabcbadaabcbacb", "aabcbacb"))
# print(s.strStr("abcddgbsbcabababerzbdj", "bcababab"))5 KMP
KMP算法一种改进的模式匹配算法,是D.E.Knuth、V.R.Pratt、J.H.Morris于1977年联合发表,KMP算法又称克努特-莫里斯-普拉特操作。它的改进在于:每当从某个起始位置开始一趟比较后,在匹配过程中出现失配,不回溯i,而是利用已经得到的部分匹配结果,将一种假想的位置定位“指针”在模式上向右滑动尽可能远的一段距离到某个位置后,继续按规则进行下一次的比较。
5.1 整体思路
KMP算法的整体思路是什么样子呢?让我们来看一组例子:
KMP算法和BF算法的“开局”是一样的,同样是把主串和模式串的首位对齐,从左到右对逐个字符进行比较。
(1)第一轮,模式串和主串的第一个等长子串比较,发现前5个字符都是匹配的,第6个字符不匹配,是一个“坏字符”:
这时候,如何有效利用已匹配的前缀 “GTGTG” 呢?
我们可以发现,在前缀“GTGTG”当中,后三个字符“GTG”和前三位字符“GTG”是相同的:
在下一轮的比较时,只有把这两个相同的片段对齐,才有可能出现匹配。这两个字符串片段,分别叫做最长可匹配后缀子串和最长可匹配前缀子串。
(2)第二轮,我们直接把模式串向后移动两位,让两个“GTG”对齐,继续从刚才主串的坏字符A开始进行比较:
按照第一轮的思路,我们来重新确定最长可匹配后缀子串和最长可匹配前缀子串:
(3)第三轮,我们再次把模式串向后移动两位,让两个“G”对齐,继续从刚才主串的坏字符A开始进行比较:
以上就是KMP算法的整体思路:在已匹配的前缀当中寻找到最长可匹配后缀子串和最长可匹配前缀子串,在下一轮直接把两者对齐,从而实现模式串的快速移动。
那么,如何找到一个字符串前缀的“最长可匹配后缀子串”和“最长可匹配前缀子串”?可以事先缓存到一个集合中,用的时候再去集合里面取。这个集合被称为next数组。
5.2 求next数组
5.2.1 next数组是什么?
next数组到底是个什么鬼呢?这是一个一维整型数组,数组的下标代表了“已匹配前缀的下一个位置”,元素的值则是“最长可匹配前缀子串的下一个位置”。
5.2.2 如何寻找前后缀,生成next
- 找前缀时,要找除了最后一个字符的所有子串。
- 找后缀时,要找除了第一个字符的所有子串。
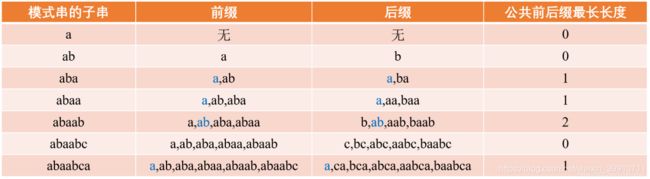
现在有串P=abaabca,各个子串的最大公共前后缀长度如下表所示:
这样,公共前后缀最长长度就会和串P的每个字符产生一种对应关系:
这个表的含义是在当前字符作为最后一个字符时,当前子串所拥有的公共前后缀最长长度。例如当c作为最后一个字符时,当前子串abaabc并没有公共前后缀。
接下来我们就用这个表来引出next数组,next 数组的值是除当前字符外(注意不包括当前字符)的公共前后缀最长长度,相当于把上表做一个变形,将表中公共前后缀最长长度全部右移一位,第一个值赋为-1。例如 c对应next值的意义是,c之前(不包括c)的子串abaab所拥有的公共前后缀最长长度为2,我们称next数组中的值为失效函数值,也就是c的失效函数值为2。
next数组如下:
5.2.3 如何生成next数组
由于已匹配前缀数组在主串和模式串当中是相同的,所以我们仅仅依据模式串,就足以生成next数组。
最简单的方法是从最长的前缀子串开始,把每一种可能情况都做一次比较。
假设模式串的长度是m,生成next数组所需的最大总比较次数是1+2+3+4+......+m-2 次。
显然,这种方法的效率非常低,如何进行优化呢?
我们可以采用类似“动态规划”的方法。首先next[0]和next[1]的值肯定是0,因为这时候不存在前缀子串;从next[2]开始,next数组的每一个元素都可以由上一个元素推导而来。
已知next[i]的值,如何推导出next[i+1]呢?让我们来演示一下上述next数组的填充过程:
(1)第一步
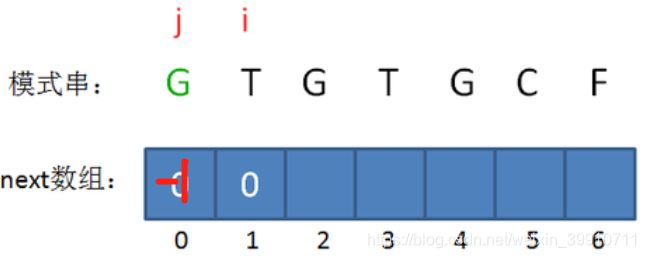
如图所示,我们设置两个变量i和j,其中i表示“已匹配前缀的下一个位置”,也就是待填充的数组下标,j表示“最长可匹配前缀子串的下一个位置”,也就是待填充的数组元素值。
当已匹配前缀不存在的时候,最长可匹配前缀子串当然也不存在,所以i=0,j=0,此时next[0] = -1。
(2)第二步
接下来,我们让已匹配前缀子串的长度加1:
此时的已匹配前缀是G,由于只有一个字符,同样不存在最长可匹配前缀子串,所以i=1,j=0,next[1] = 0。
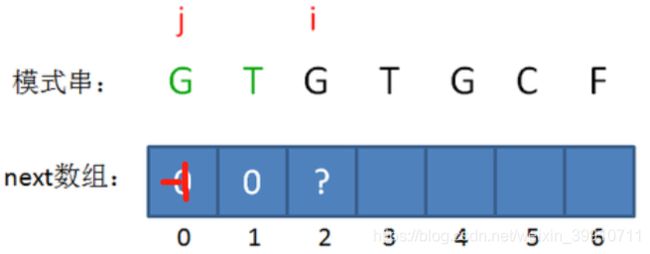
(3)第三步
接下来,我们让已匹配前缀子串的长度继续加1:
此时的已匹配前缀是GT,我们需要开始做判断了:由于模式串当中 pattern[j] != pattern[i-1],即G!=T,最长可匹配前缀子串仍然不存在。
所以当 i=2 时,j 仍然是0,next[2] = 0。
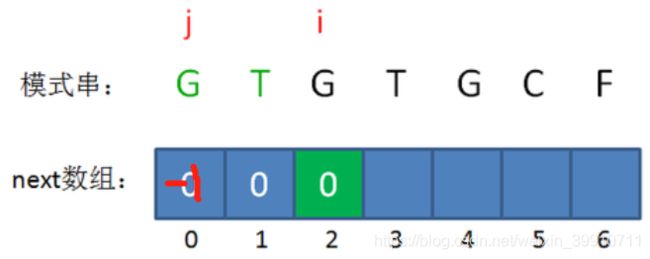
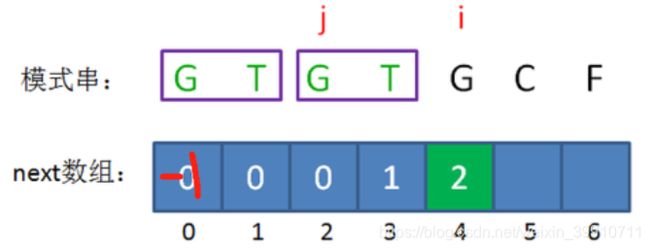
(4)第四步
接下来,我们让已匹配前缀子串的长度继续加1:
此时的已匹配前缀是GTG,由于模式串当中 pattern[j] = pattern[i-1],即G=G,最长可匹配前缀子串出现了,是G。
所以当i=3时,j=1,next[3] = next[2]+1 = 1。
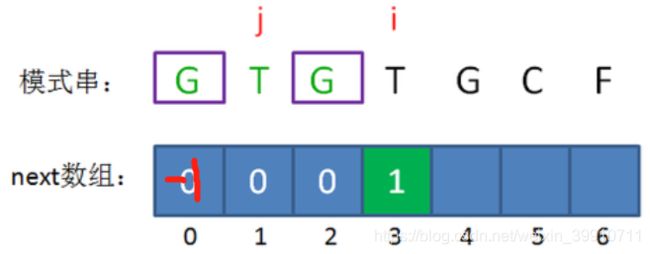
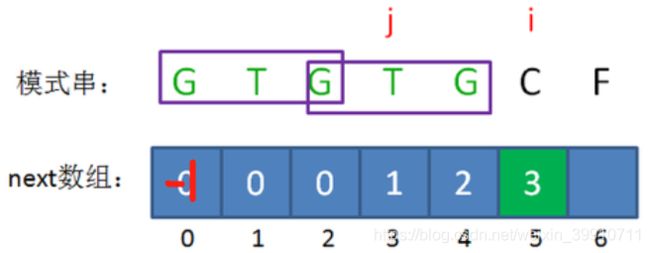
(4)第四步
接下来,我们让已匹配前缀子串的长度继续加1:
此时的已匹配前缀是GTGT,由于模式串当中 pattern[j] = pattern[i-1],即T=T,最长可匹配前缀子串又增加了一位,是GT。
所以当i=4时,j=2,next[4] = next[3]+1 = 2。
(5) 第五步
接下来,我们让已匹配前缀子串的长度继续加1:
此时的已匹配前缀是GTGTG,由于模式串当中 pattern[j] = pattern[i-1],即G=G,最长可匹配前缀子串又增加了一位,是GTG。
所以当i=5时,j=3,next[5] = next[4]+1 = 3。
(6)第六步
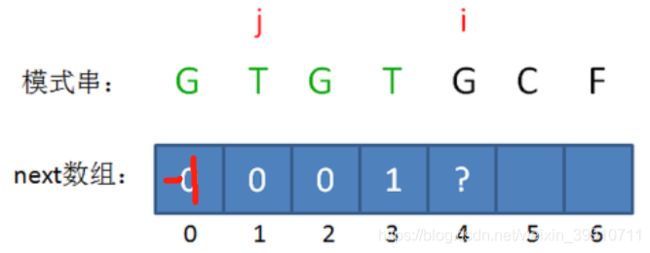
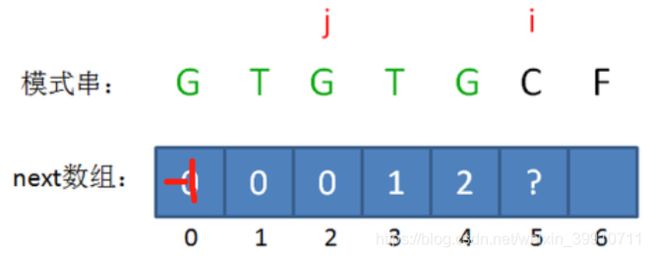
接下来,我们让已匹配前缀子串的长度继续加1:
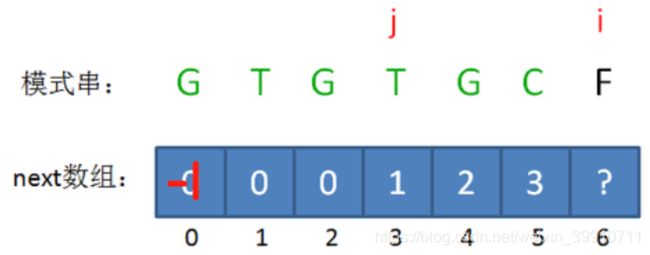
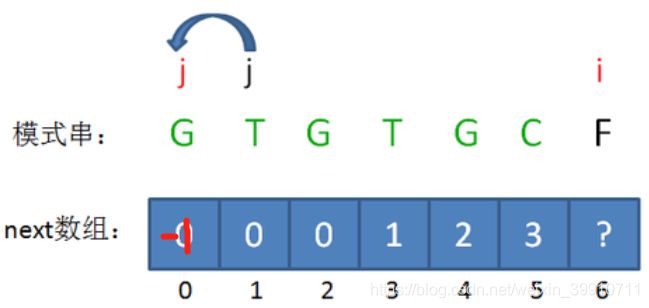
此时的已匹配前缀是GTGTGC,这时候需要注意了,模式串当中 pattern[j] != pattern[i-1],即T != C,这时候该怎么办呢?
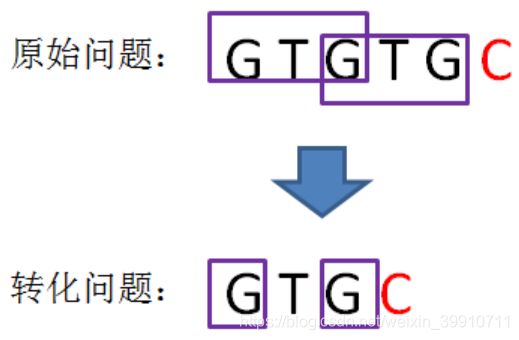
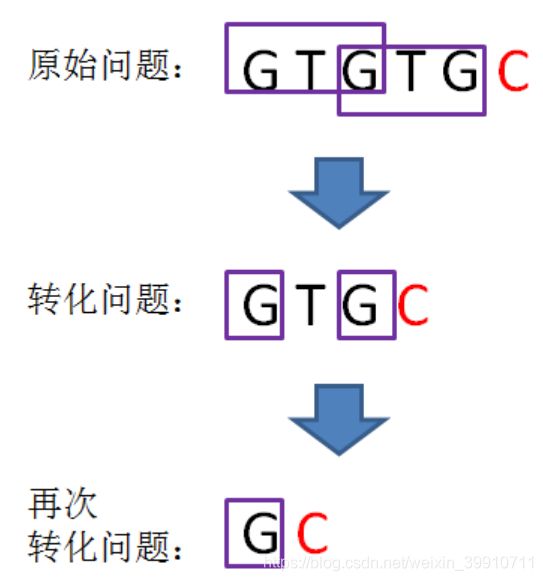
这时候,我们已经无法从next[5]的值来推导出next[6],而字符C的前面又有两段重复的子串“GTG”。那么,我们能不能把问题转化一下?
或许听起来有些绕:我们可以把计算“GTGTGC”最长可匹配前缀子串的问题,转化成计算“GTGC”最长可匹配前缀子串的问题。
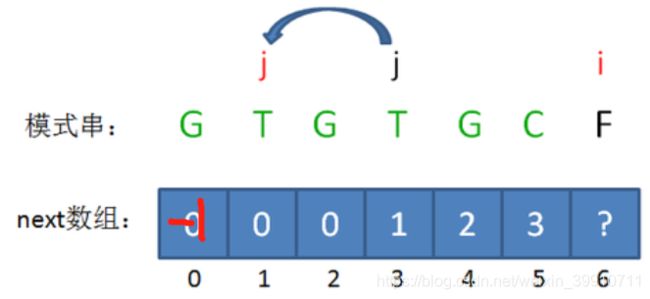
这样的问题转化,也就相当于把变量j回溯到了next[j],也就是 j=next[j] 的局面(i值不变):
回溯后,情况仍然是 pattern[j] != pattern[i-1],即T!=C。那么我们可以把问题继续进行转化:
问题再次的转化,相当于再一次把变量j回溯到了next[j],也就是j=0的局面:
回溯后,情况仍然是 pattern[j] != pattern[i-1],即G!=C。j 已经不能再次回溯了,所以我们得出结论:i=6时,j=0,next[6] = 0。
5.3 KMP实现
1. 对模式串预处理,生成next数组
2. 进入主循环,遍历主串
2.1. 比较主串和模式串的字符
2.2. 如果发现坏字符,查询next数组,得到匹配前缀所对应的最长可匹配前缀子串,移动模式串到对应位置
2.3.如果当前字符匹配,继续循环
Python实现:
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
# @Time : 2021/8/16 19:47
# @Author : song.xiangyu
class Solution:
def strStr(self, haystack, needle):
# def get_next(needle):
# next = [-1, 0]
# m = len(needle)
# j = 0
# for i in range(1, m-1):
# if needle[j] == needle[i]:
# j += 1
# else:
# while next[j] != -1 and needle[j] != needle[i]:
# j = next[j]
# if needle[j] == needle[i]:
# j += 1
# next.append(j)
# return next
def get_next(substring):
next = [-1]
i = 0
j = -1
while i < len(substring) - 1:
if j == -1 or substring[i] == substring[j]:
i += 1
j += 1
next.append(j)
else:
j = next[j]
return next
next = get_next(needle)
print(next)
# 进行匹配
n = len(haystack)
m = len(needle)
i = 0
j = 0
while i < n and j < m:
# while j < m:
if j == -1 or haystack[i] == needle[j]:
i += 1
j += 1
else:
j = next[j]
if j == m:
return i - j
else:
return -1
s = Solution()
# print(s.strStr("aabcbadaabcbacd", "aabcbacb"))
print(s.strStr("abcddgbsbcabababerzbdj", "bcababab"))
print(s.strStr("abcddgbsbcahihibababerzbdj", "bcbcababab"))- 空间复杂度:KMP算法唯一的额外空间是next数组,假设模式串长度是m,那么算法的空间复杂度就是o(m)。
- 时间复杂度:KMP算法包括两步,第一步生成next数组,时间复杂度可以估算为o(m);第二步的主循环是对主串的遍历,时间复杂度可以估算为o(n),因此,KMP算法的整体时间复杂度是o(m+n),其中m是模式串长度,n是主串长度。
漫画:什么是字符串匹配算法?https://mp.weixin.qq.com/s?__biz=MzIxMjE5MTE1Nw%3D%3D&chksm=8c99d02cbbee593ae0fb7fa1c8c610e7c1f57009e0c0ecbe19d07f60951912c915bce65c8619&idx=1&mid=2653201142&scene=21&sn=8cac1bbcfdb94474f0cc3855705cc253#wechat_redirect
BM:
【算法】字符串匹配2 BM算法 坏字符规则 好后缀规则 python代码实现:https://blog.csdn.net/sscc_learning/article/details/89568045
字符串匹配的Boyer-Moore算法:http://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html
从入门到精通之Boyer-Moore字符串搜索算法详解:https://cloud.tencent.com/developer/article/1088330
KMP:
漫画:什么是KMP算法?:https://baijiahao.baidu.com/s?id=1659735837100760934&wfr=spider&for=pc
KMP算法详解: https://blog.csdn.net/yyzsir/article/details/89462339