上采样相关技术
一、参考资料
上采样和上卷积的区别
怎样通俗易懂地解释反卷积?
卷积和池化的区别、图像的上采样(upsampling)与下采样(subsampled)
[读论文]用全卷积Res网络做深度估计
对抗生成网络GAN系列——DCGAN简介及人脸图像生成案例
深度学习中常用的几种卷积(上篇):标准二维卷积、转置卷积、1*1卷积(附Pytorch测试代码)
二、相关介绍
1. 上采样与下采样
无论下采样(缩放图像)还是上采样(放大图像),采样方式有很多种。如最近邻插值,双线性插值,均值插值,中值插值等方法。
1.1 上采样(Upsample)
在应用在计算机视觉的深度学习领域,由于输入图像通过卷积神经网络(CNN)提取特征后,输出的尺寸往往会变小,而有时我们需要将图像恢复到原来的尺寸以便进行进一步的计算(e.g.图像的语义分割)。这个采用扩大图像尺寸,实现图像由小分辨率到大分辨率的映射的操作,叫做上采样(Upsample)。上采样,又称为图像插值(interpolating),即为放大图像的过程。
上采样有3种常见的方法:双线性插值(bilinear interpolation),转置卷积(Transposed Convolution),反池化(Unpooling)。
1.2 下采样(subsample)
下采样又称为降采样(downsample),主要目的是缩小图像尺寸,使得图像符合显示区域的大小,或者生成对应图像的缩略图。在计算机视觉中,CNN特征提取过程即为下采样过程。
对于一幅图像I尺寸为M*N,对其进行s倍下采样,即得到(M/s)*(N/s)尺寸的得分辨率图像,当然s应该是M和N的公约数才行,如果考虑的是矩阵形式的图像,就是把原始图像s*s窗口内的图像变成一个像素,这个像素点的值就是窗口内所有像素的均值
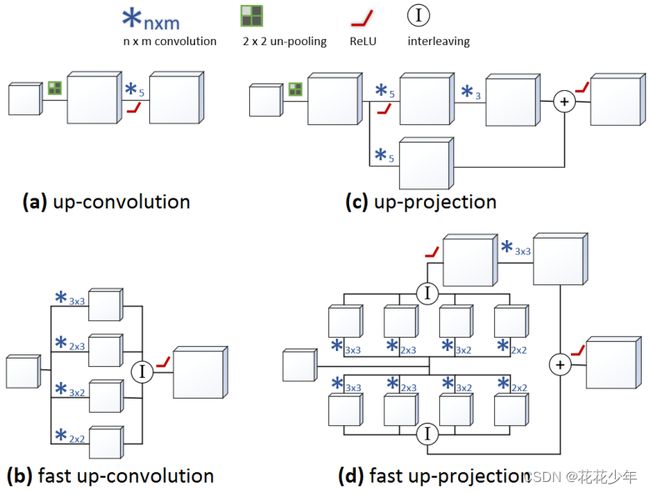
2. 上卷积(Up-convolution)
upconv上卷积是什么? monodepth源码阅读
Deeper Depth Prediction with Fully Convolutional Residual Networks
2.1 方法一(base版)
Up-convolution,又称为upconv,是通过插值增加特征图的空间分辨率。其结构如下图所示: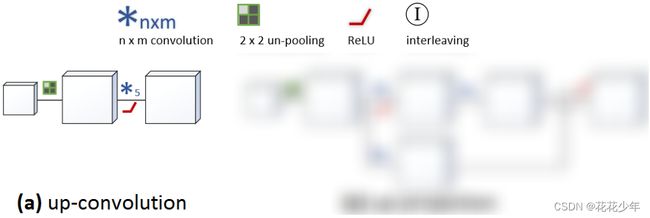

Up-convolution包含三个过程:
- un-pooling上池化过程。把特征图中的一个元素映射成2×2的大小,左上角是这个元素,其他三个格子都是零;
- 卷积过程。用5×5的卷积进行卷积计算;
- ReLu激活过程。
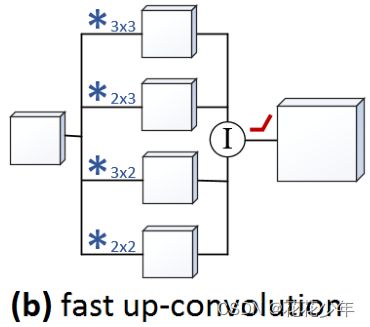
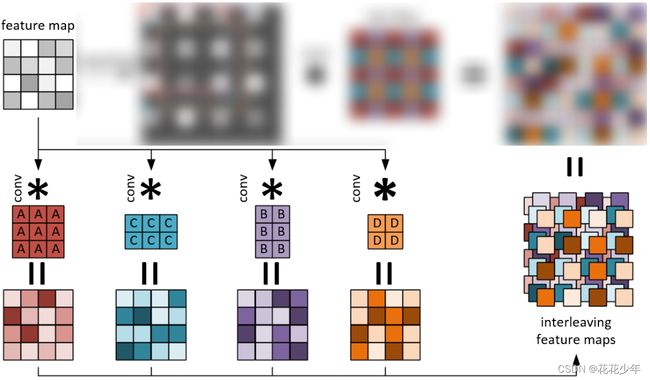
2.2 方法二(改进版)
Deeper Depth Prediction with Fully Convolutional Residual Networks
基于base版本改进的fast up-convolution,其
3. Deconvolution
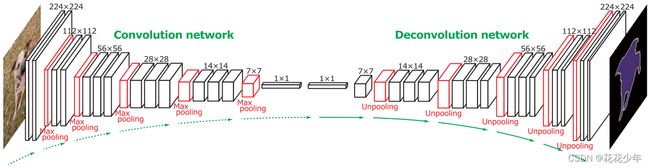
Learning deconvolution network for semantic segmentation
4. 上投影(up-projection)
Deeper Depth Prediction with Fully Convolutional Residual Networks
We call this new up-sampling block up-projection since it extends the idea of the projection connection to up-convolutions.
5. convolution+pooling
卷积+池化操作,构成convolution+pooling层。
6. unpooling+convolution
是convolution+pooling的逆向操作,构成unpooling+convolution层。
三、上采样相关方法
1. 转置卷积(Transposed Convolution)
怎样通俗易懂地解释反卷积?
转置卷积(Transposed Convolution)
抽丝剥茧,带你理解转置卷积(反卷积)
1.1 引言
对于很多生成模型(如GAN中的生成器、自动编码器(Autoencoder)、语义分割等模型),我们通常希望进行与正常卷积相反的转换,即我们希望执行上采样,比如自动编码器或者语义分割。(对于语义分割,首先用编码器提取特征图,然后用解码器回复原始图像大小,这样来分类原始图像的每个像素。)实现上采样的传统方法是应用插值方案或人工创建规则。而神经网络等现代架构则倾向于让网络自己自动学习合适的变换,无需人类干预。为了做到这一点,我们可以使用转置卷积。
1.2 转置卷积的概念
转置卷积(Transposed Convolution) 在语义分割或者对抗神经网络(GAN)中比较常见,其主要作用是做上采样(UpSampling)。
转置卷积又叫反卷积、逆卷积。不过转置卷积是目前最为正规和主流的名称,因为这个名称更加贴切的描述了卷积的计算过程,而其他的名字容易造成误导。在主流的深度学习框架中,如TensorFlow,Pytorch,Keras中的函数名都是conv_transpose。所以学习转置卷积之前,我们一定要弄清楚标准名称,遇到他人说反卷积、逆卷积也要帮其纠正,让不正确的命名尽早的淹没在历史的长河中。
我们先说一下为什么人们很喜欢将转置卷积称为反卷积或逆卷积。首先举一个例子,将一个4x4的输入通过3x3的卷积核在进行普通卷积(无padding, stride=1),将得到一个2x2的输出。而转置卷积将一个2x2的输入通过同样3x3大小的卷积核将得到一个4x4的输出,看起来似乎是普通卷积的逆过程。就好像是加法的逆过程是减法,乘法的逆过程是除法一样,人们自然而然的认为这两个操作似乎是一个可逆的过程。转置卷积不是卷积的逆运算(一般卷积操作是不可逆的),转置卷积也是卷积。对于同一个卷积核,经过转置卷积操作之后只能恢复到原来的大小(shape),数值与原来不同。所以转置卷积的名字就由此而来,而并不是“反卷积”或者是“逆卷积”,不好的名称容易给人以误解。
转置卷积和直接卷积有很大的区别,直接卷积是用一个“小窗户”去看一个“大世界”,而转置卷积是用一个“大窗户”的一部分去看“小世界”。
1.3 转置卷积操作
转置卷积核大小为k,步长s,填充p,则转置卷积的运算步骤可以归为以下几步:
- 首先,在元素间填充s-1个零元素(等于0不用填充);
- 然后,在特征图四周填充k-p-1个零元素;
- 接着,对卷积核进行上下、左右翻转;
- 最后,以stride=1,padding=0,做卷积操作。
1.4 转置卷积示例
假设,输入层为2x2,转置卷积核大小为k=3,步长stride=1,填充padding=0,通过转置卷积后,得到大小4x4的特征图。

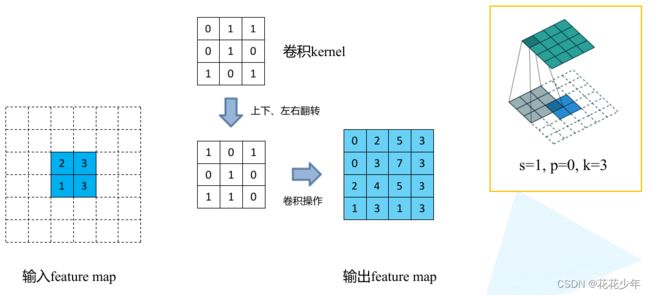
值得一提的是,可以通过改变padding和stride,将2x2的输入映射到不同的图像尺寸。如下图,stride=2,则在元素间填充1个零元素;padding=0,则在特征图四周填充2个零元素。通过转置卷积后,得到大小5x5的特征图。
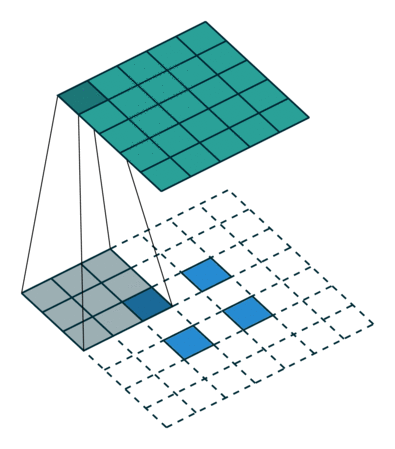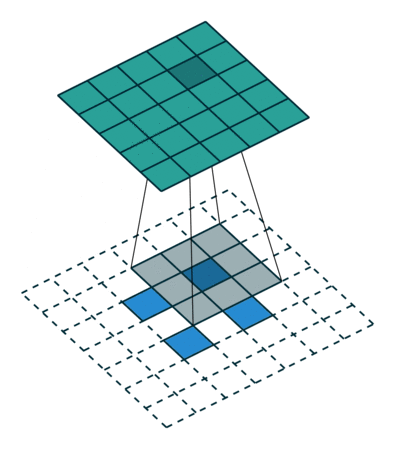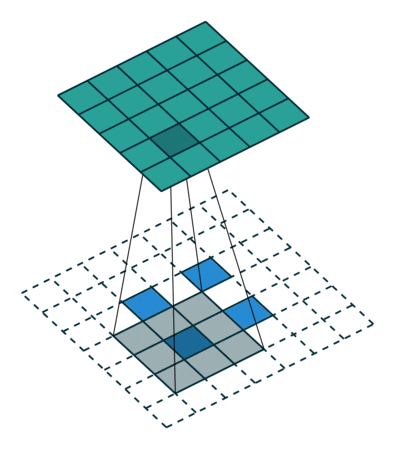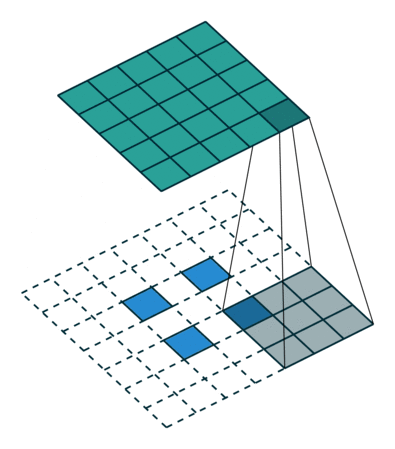
1.5 棋盘效应(Checkerboard Artifacts)
棋盘效应(Checkerboard Artifacts)
卷积操作总结(三)—— 转置卷积棋盘效应产生原因及解决
Deconvolution and Checkerboard Artifacts
棋盘效应是由于转置卷积的“不均匀重叠”(Uneven overlap)的结果,使图像中某个部位的颜色比其他部位更深。
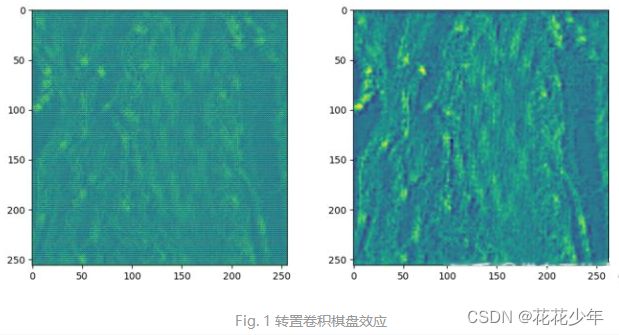
1.6 代码实现
import torch
import torch.nn as nn
def transposed_conv_official():
feature_map = torch.as_tensor([[1, 0],
[2, 1]], dtype=torch.float32).reshape([1, 1, 2, 2])
print(feature_map)
trans_conv = nn.ConvTranspose2d(in_channels=1, out_channels=1,
kernel_size=3, stride=1, bias=False)
trans_conv.load_state_dict({"weight": torch.as_tensor([[1, 0, 1],
[0, 1, 1],
[1, 0, 0]], dtype=torch.float32).reshape([1, 1, 3, 3])})
print(trans_conv.weight)
output = trans_conv(feature_map)
print(output)
def transposed_conv_self():
feature_map = torch.as_tensor([[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0],
[0, 0, 2, 1, 0, 0],
[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0]], dtype=torch.float32).reshape([1, 1, 6, 6])
print(feature_map)
conv = nn.Conv2d(in_channels=1, out_channels=1,
kernel_size=3, stride=1, bias=False)
conv.load_state_dict({"weight": torch.as_tensor([[0, 0, 1],
[1, 1, 0],
[1, 0, 1]], dtype=torch.float32).reshape([1, 1, 3, 3])})
print(conv.weight)
output = conv(feature_map)
print(output)
def main():
transposed_conv_official()
print("---------------")
transposed_conv_self()
if __name__ == '__main__':
main()
输出结果
tensor([[[[1., 0.],
[2., 1.]]]])
Parameter containing:
tensor([[[[1., 0., 1.],
[0., 1., 1.],
[1., 0., 0.]]]], requires_grad=True)
tensor([[[[1., 0., 1., 0.],
[2., 2., 3., 1.],
[1., 2., 3., 1.],
[2., 1., 0., 0.]]]], grad_fn=<SlowConvTranspose2DBackward>)
---------------
tensor([[[[0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0.],
[0., 0., 1., 0., 0., 0.],
[0., 0., 2., 1., 0., 0.],
[0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0.]]]])
Parameter containing:
tensor([[[[0., 0., 1.],
[1., 1., 0.],
[1., 0., 1.]]]], requires_grad=True)
tensor([[[[1., 0., 1., 0.],
[2., 2., 3., 1.],
[1., 2., 3., 1.],
[2., 1., 0., 0.]]]], grad_fn=<ThnnConv2DBackward>)
Process finished with exit code 0
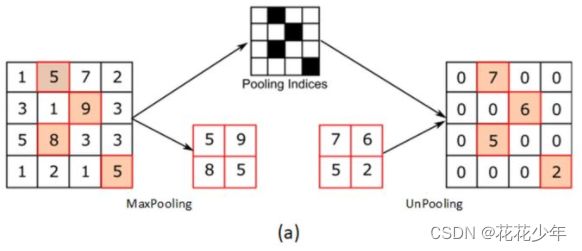
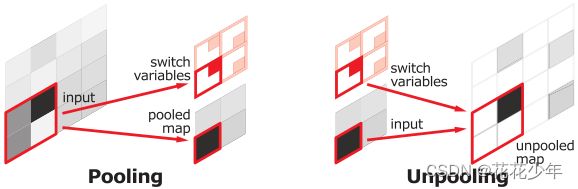
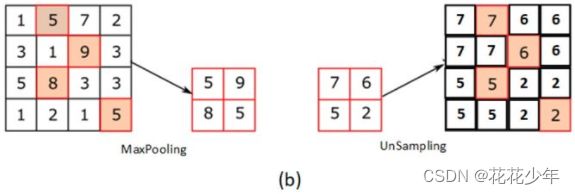
2. 反池化(Unpooling)
Unpooling是pooling操作的逆向过程,可以提高特征图的空间分辨率。
2.1 方法一
2.2 方法二
Learning to Generate Chairs with Convolutional Neural Networks
Deeper Depth Prediction with Fully Convolutional Residual Networks
用2x2的块进行反池化操作,左上角为实值,其他补0。
2.3 方法三
Adaptive Deconvolutional Networks for Mid and High Level Feature Learning
在卷积神经网络中,最大池化操作是不可逆的,但可以通过一组转换变量来记录每个池化区域内最大值的位置,从而获得近似的反池化。
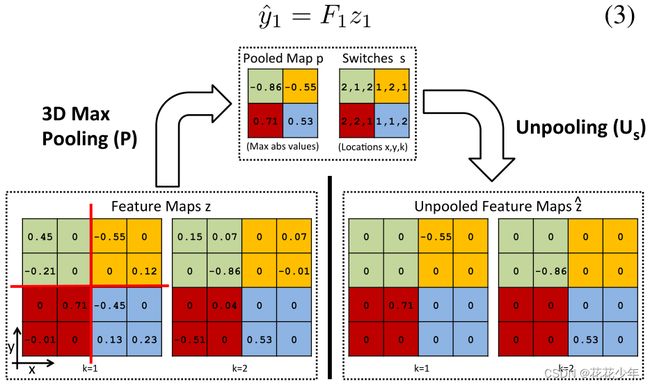
3D最大池化。特征图z划分为2x2的区域,每个区域用不同颜色表示。对每个区域进行最大池化操作,得到池化图p和转换图s。其中,k表示维度,转换图s记录了每个区域最大值的位置。
2.4 方法四
Visualizing and Understanding Convolutional Networks
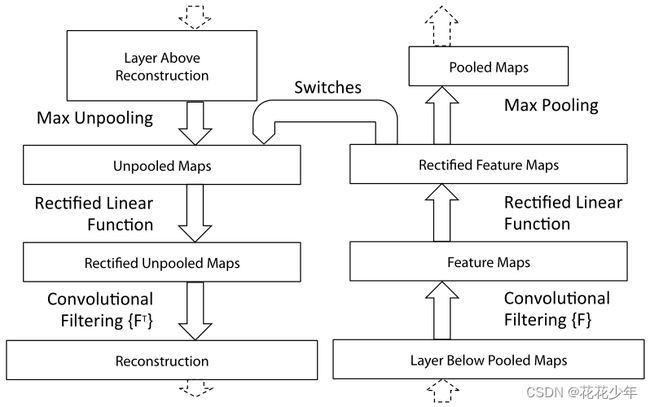

2.5 方法五
Learning deconvolution network for semantic segmentation