很重要的数据结构
很重要的数据结构
文章目录
- 很重要的数据结构
-
- 1 数组
-
-
- 1. 1 数组特点:
-
- 2 链表
-
-
- 2.1链表特点:
- 2.2 单项链表
- 2.3 双向链表
-
- 3 二叉树
-
-
- 3.1 二叉树特点
- 3.2 二叉树的分支
- 3.3 遍历操作
- 3.4 删除结点
- 3.5 查找局限性
-
- 4 `AVL`树(平衡二叉树)
-
-
- 4.1 描述:
-
- 5 `2-3-4`树
-
-
- 5.1 描述
- 5.2 生成的过程
- 5.3 和红黑树的等价关系
-
- 5.3.1 `2结点`
- 5.3.2 `3结点`
- 5.3.3 `4结点`
-
- 6 红黑树
-
-
- 6.1描述
- 6.2 旋转描述
-
- 6.2.1 概念讲解
- 6.3 新增结点
- 6.4 234树删除操作
- 6.5 红黑树删除
-
- 7 [Trie树](https://baike.baidu.com/item/Trie树)
视频链接 阿里P7大佬手撕红黑树全套教程-(二叉树、哈希、B+树、Hash、平衡算法、数据结构)
1 数组
1. 1 数组特点:
- 内存地址连续
- 申请较大内存需要完整的内存块
- 可以通过下标进行成员访问,下标访问的性能高
- 增删的消耗高,如果数组越界,还会需要扩容
2 链表
2.1链表特点:
- 链表也是顺序存储数据,不过在内存上不是连续的
- 链表分为单项链表,双向链表
2.2 单项链表
- 单项链表只保存下一个节点的指针/引用
- 单向链表查询 耗时
- 单向链表的插入和删除操作方便
2.3 双向链表
- 双向保存上一个节点和下一个节点,
- 查询效率高于单向链表
- 插入和删除操作也很方便
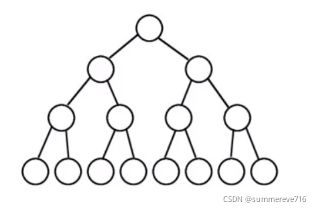
3 二叉树
3.1 二叉树特点
- 每个子结点只有两个结点的树,每个结点至多拥有两课子树(即二叉树中不存在度大于2的节点),并且,二叉树的子树有左右之分,其次序不能任意颠倒
- 任意结点左子树不为空,则左子树的值均小于根节点的值
- 任意结点右子树不为空,则右子树的值均大于根节点的值
- 任意结点的左右子树都是二叉树
- 二叉树不存在键值相等的结点
- 树的深度就是根节点到叶子节点的最大高度
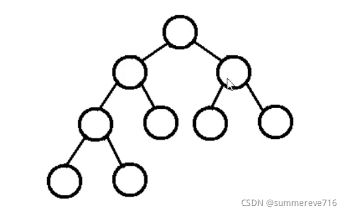
3.2 二叉树的分支
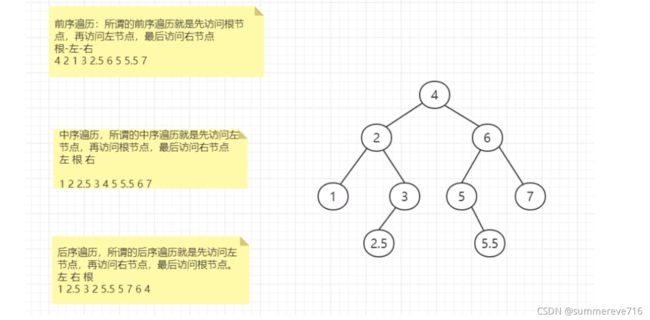
3.3 遍历操作
- 查找最小值: 沿着左子树一直查找,最后一个就是最小值
- 查找最大值: 沿着右子树一直查找,最后一个就是最大值
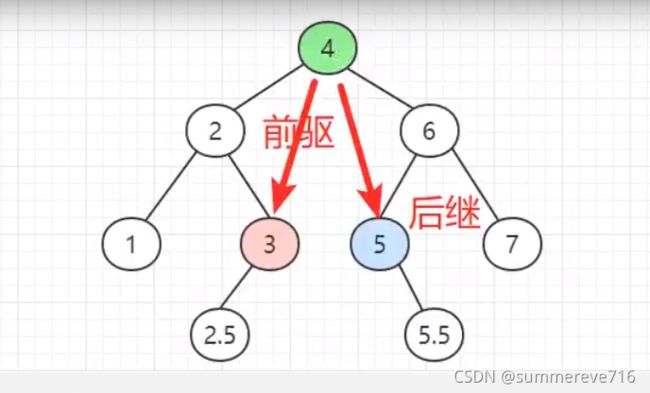
- 查找前驱节点:小于当前结点的最大值,结点左边右子树查找,最大值 (非叶子节点)
- 查找后继节点:大于当前结点的最小值。结点右边左子树查找,最小值(非叶子节点)
前驱节点,按照中序排列后,当前结点前面的为前驱,后面的为后继结点
因为也可以网上找,比如叶子结点的前驱和后继都在上面
/**
* 获取前驱结点
* 1. 如果当前结点有左子节点,则遍历左子节点的右树,最大值就是前驱节点
* 2. 如果没有左子节点,则找父节点,并且父节点的 左子结点 不是自身的点(就是向上找到没有左结点的给结点)
**/
private TreeNode getPresursor(final TreeNode node){
if ( node == null ) return null;
if ( node.getLeft() == null ){
//往上面找
TreeNode _node = node;
TreeNode parent = _node.getParent();
while( parent != null && parent.getLeft() != _node){
_node = parent;
parent = _node.getParent();
}
return _node;
}
else{
TreeNode _node = node.getLeft();
while( _node.getRight() != null ){
_node = _node.getRight();
}
return _node;
}
}
/**
* 获取后继节点
* * 1. 如果当前结点有 [右子节点],则遍历 [右子节点]的 [左树],最小值就是后继节点
* * 2. 如果没有 [右子节点],则找父节点,并且父节点的 右 不是自身的点(就是向上找到没有 [右节点] 的给结点)
*/
private TreeNode getSuccessor(final TreeNode node ){
if ( node == null ) return null;
if ( node.getRight() == null ){
TreeNode parent = node.getParent();
TreeNode _node = node;
while( parent!= null && parent.getRight() != _node){
_node = parent;
parent = _node.getParent();
}
return _node;
}
else{
TreeNode _node = node.getRight();
while( _node.getLeft() != null ){
_node = _node.getLeft();
}
return _node;
}
}
3.4 删除结点
二叉树中删除结点:本质上是找前驱节点或者后继结点来替代
- 叶子节点直接删除
- 只有一个子结点的用其子结点替代(本质上就是找到前驱结点或者后继节点,左节点就是前驱节点,右节点就是后继节点)
- 有两个结点的,需要找到替代结点(提到节点就是前驱节点或者后继节点)
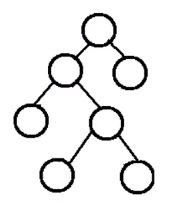
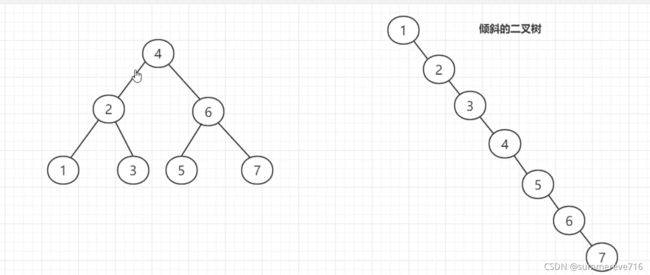
3.5 查找局限性
- 如果不凑巧,二叉树会变成倾斜二叉树,,线性链(双向链表)
public class TreeNode<T extends Comparable<T>> implements myBaseNode {
private TreeNode parent;
private TreeNode left;
private TreeNode right;
private T value;
public TreeNode(T value) {
this.value = value;
}
//设置左子结点,则左子结点的父节点就是this
public void setLeft(TreeNode node){
left = node;
if ( node != null ){
node.parent = this;
}
}
//设置右子结点,则右子结点的父节点就是this
public void setRight(TreeNode node){
right = node;
if ( node != null ){
node.parent = this;
}
}
public TreeNode left(){
return left;
}
public TreeNode right(){
return right;
}
public T getValue(){
return this.value;
}
public TreeNode getParent(){
return parent;
}
//比较数据
public int compareValue(T v){
return v.compareTo(value);
}
//从父节点删除自身,并且返回父节点
public TreeNode removeFromParent(){
return replaceFromParent(null);
}
//从父节点处使用指定的结点替换自己
public TreeNode replaceFromParent(TreeNode node){
if ( parent == null ){
//基本上就是根节点
node.parent = parent ;
return parent;
}
if ( parent.left == this ){
parent.setLeft(node);
}
else{
parent.setRight(node);
}
return parent;
}
public void setValue(T value) {
this.value = value;
}
}
/**
* 描述: []
* 创建时间: 2021/8/3122:40
*
* @Author LDJ
* @Version v1.0
* @update [2021/8/31 22:40] [LDJ][变更描述]
**/
//二叉树节点
public class myTreeNodeDemo<T extends Comparable<T>> {
//根节点
private TreeNode root = null;
//添加
public TreeNode add(T value){
if ( value == null ){
throw new RuntimeException("value not be null");
}
if ( root == null ){ //如果当前root == null, 直接添加到父节点
root = createTreeNode(value);
return root;
}
//新建的结点
TreeNode node = createTreeNode(value);
//指向当前根节点
TreeNode last = root;
int compareValue = 0;
while (true ){
compareValue = last.compareValue( value); //对比当前添加的对象和已有的对象,如果一样则不能添加
if ( compareValue == 0){
//不能一样,添加失败
return null;
}
else if ( compareValue >0){ //大于,则放在右子树
if ( last.right() == null ){
last.setRight(node); //先判断当前的结点上有没有数据,有则对比大小,看是左子树还是右子树
break; //如果没有数据则直接添加,并且设置node的parent为last
} //
else{ //
last = last.right();
continue;
}
}
else { //小于放在左子树
if ( last.left() == null ){
last.setLeft(node);
break;
}
else
{
last = last.left();
continue;
}
}
}
return node;
}
//创建结点
TreeNode createTreeNode(T value ){
return new TreeNode( value);
}
//获取最左结点 //用于中序和后续排列需要
private TreeNode getLeft( TreeNode node ){
if ( node.left() == null ) return node;
return getLeft(node.left());
}
/**
* 获取前驱结点
* 1. 如果当前结点有左子节点,则遍历左子节点的右树,最大值就是前驱节点
* 2. 如果没有左子节点:
* 2.1 若该节点是其父节点的右边孩子,那么该节点的前驱结点即为其父节点。
* 2.2 若该节点是其父节点的左边孩子,那么需要沿着其父亲节点一直向树的顶端寻找
**/
private TreeNode getPresursor(final TreeNode node){
if ( node == null ) return null;
if ( node.left() == null ){
//往上面找
TreeNode _node = node;
TreeNode parent = _node.getParent();
while( parent != null && parent.left() == _node){
_node = parent;
parent = _node.getParent();
}
return parent;
}
else{
TreeNode _node = node.left();
while( _node.right() != null ){
_node = _node.right();
}
return _node;
}
}
/**
* 获取后继节点
* 1. 如果当前结点有 [右子节点],则遍历 [右子节点]的 [左树],最小值就是后继节点
* 2. 如果没有 [右子节点]:
* 2.1 若该节点是其父节点的左边孩子,那么该节点的后继结点即为其父节点。
* 2.2 若该节点是其父节点的右边孩子,那么需要沿着其父亲节点一直向树的顶端寻找
*/
private TreeNode getSuccessor(final TreeNode node ){
if ( node == null ) return null;
if ( node.right() == null ){
TreeNode parent = node.getParent();
TreeNode _node = node;
while( parent!= null && parent.right() == _node){
_node = parent;
parent = _node.getParent();
}
return parent;
}
else{
TreeNode _node = node.right();
while( _node.left() != null ){
_node = _node.left();
}
return _node;
}
}
/**
* 删除结点
* 1. 如果当前删除的节点是叶子节点,直接删除
* 2. 找到前驱节点/后继节点,替换
* 1. 如果替换的节点x是叶子节点,直接 替换
* 2. 如果节点x不是叶子节点,需要找他的子结点替换节点x
*
**/
public void deleteNode(T value){
//先查找
TreeNode node = find(root,value); // 现根据value查找到结点所在位置,
if ( node == null){
return; //找不到就算了,不删除了
}
//叶子节点
if ( node.left() == null && node.right() == null){ //没有子节点的是叶子节点,包括单个的root结点
//直接删除
node.removeFromParent();//从parent上移除自己
}
else{
//使用前驱结点或者后继结点替代
TreeNode nextNode = getPresursor(node); //获取前驱结点(左边最大的结点->左边找右子树)
if ( nextNode == null ){
nextNode = getSuccessor(node); //获取后继结点(右边最小的结点->右边找左子树)
}
if ( nextNode == null ){
//找不到替换节点,
throw new RuntimeException("找不到替换节点");
}
//替换node
node.setValue(nextNode.getValue());
//判断替换节点是否是叶子节点
if ( nextNode.left() !=null && nextNode.right() != null ){
//替换节点是叶子节点,不管了
nextNode.removeFromParent();
}
else
{
TreeNode replacementNode = nextNode.left()==null?nextNode.right():nextNode.left();
//将replacementNode 替换nextNode
nextNode.replaceFromParent(replacementNode);
}
}
}
//根据数值查找结点
//使用递归的调用方式
private TreeNode find(TreeNode node ,T value){
if ( node != null ){
int res = node.compareValue(value);
if ( res ==0 ){
return node;
}
else if ( res > 0 ){
return find( node.right(),value);
}
else{
return find( node.left(),value);
}
}
return null;
}
//前序排列
public void show_qx(TreeNode node ){
if ( node == null ){
return ;
}
System.out.print(node.getValue()+ " ");
show_qx(node.left());
show_qx(node.right());
}
//显示中序排列,目前还有问题,等会完善
public void show_zx(TreeNode node ){
if ( node == null ){
return ;
}
show_zx(node.left());
System.out.print(node.getValue() + " ");
show_zx(node.right());
}
//跟 左 右
/*
①先输出节点的值,然后将节点入栈
②然后判断节点的左子节点是否为空,如果不为空,则继续循环①;如果为空,则证明这一条线路上的节点值已经被遍历完了,
则跳出循环进行出栈操作,只要栈不为空,则节点出栈,并让节点等于他的右子节点,继续进行①号循环
③直到所有节点都已经出栈,且循环到节点为空,则遍历结束
Stack 是vector的子类
*/
public void show_qx_strack(TreeNode node){
StringBuffer buffer = new StringBuffer("\r\n");
//声明一个栈
Stack<TreeNode> stack = new Stack<>();
if ( node == null){
return;
}
TreeNode t = node;
while(t != null || !stack.isEmpty()){
while( t != null ){
buffer.append(t.getValue()).append(" ");
stack.push(t);
t = t.left();
}
if ( !stack.isEmpty()){
t = stack.pop();
t = t.right();
}
}
System.out.println(buffer.toString());
}
//显示后续排列,目前还有问题,等会完善
public void show_hx(TreeNode node ){
if ( node == null ){
return ;
}
show_hx(node.left());
show_hx(node.right());
System.out.print(node.getValue() + " ");
}
//以该节点作为旋转指点,进行左旋
private void turnLeft(TreeNode node){
if ( node == null )return;
//如果右子节点是空的,无法移动
if ( node.right() == null ) return;
TreeNode rightNode = node.right();
//先将当前node从它父节点上替换,
//同时更新rightNode 的父节点
//返回的就是rightNode新的父节点
TreeNode parent = node.replaceFromParent(rightNode);
if ( parent == null ){
//更新root结点
root = rightNode;
}
//将右子结点设置为当前结点的父节点
node.setRight( rightNode.left());
//删除rightNode 的左节点
rightNode.setLeft(node);
}
//以该节点作为旋转指点,进行右旋
private void turnRight(TreeNode node){
if ( node == null) return ;
//如果左子节点是空的,无法左旋
if ( node.left() == null) return;
TreeNode leftNode = node.left();
//先将当前node从它父节点上替换,
//同时更新rightNode 的父节点
//返回的就是rightNode新的父节点
TreeNode parent = node.replaceFromParent(leftNode);
if ( parent == null ){
root = leftNode;
}
//将左子结点的右子节点设置为旋转节点的左子节点
node.setLeft( leftNode.right());
//将旋转结点放在leftNode的左子节点上
leftNode.setLeft(node);
}
//测试前驱节点
@Test
public void testPredecessor(){
myTreeNodeDemo<Integer> demo = new myTreeNodeDemo<>();
demo.add(1);
demo.add(2);
TreeNode d3 = demo.add(3);
System.out.println(getPresursor(d3).getValue());
System.out.println(getSuccessor(d3)==null?"null":"ok");
}
//测试左旋
@Test
public void testTurnLeft(){
myTreeNodeDemo<Integer> demo = new myTreeNodeDemo<>();
demo.add(1);
demo.add(2);
demo.add(3);
System.out.println("前序排列");
demo.show_qx(demo.root);
//左旋
demo.turnLeft(demo.root);
//前序排列
demo.show_qx(demo.root);
demo.turnRight(demo.root);
//前序排列
demo.show_qx(demo.root);
}
@Test
public void testBl(){
myTreeNodeDemo<Double> demo = new myTreeNodeDemo<>();
demo.add(4.0);
demo.add(2.0);
demo.add(1.0);
demo.add(3.0);
demo.add(6.0);
demo.add(5.0);
demo.add(7.0);
demo.add(2.5);
demo.add(5.5);
//前序排列
System.out.println("前序排列");
demo.show_qx(demo.root);
demo.show_qx_strack(demo.root);
//中序排列
System.out.println("\n中序排列");
demo.show_zx(demo.root);
//后续排列
System.out.println("\r\n后续排列");
demo.show_hx(demo.root);
}
@Test
public void test(){
myTreeNodeDemo<Double> demo = new myTreeNodeDemo<>();
demo.add(4.0);
demo.add(2.0);
demo.add(1.0);
demo.add(3.0);
demo.add(6.0);
demo.add(5.0);
demo.add(7.0);
demo.add(2.5);
demo.add(5.5);
//前序排列
System.out.println("前序排列");
demo.show_qx(demo.root);
//中序排列
System.out.println("中序排列");
// demo.show_zx();
System.out.println("root的前驱节点");
System.out.println(demo.getPresursor(demo.root).getValue());
System.out.println("根节点的后驱结点");
System.out.println(demo.getSuccessor(demo.root).getValue());
//删除结点
System.out.println("前序排列");
demo.deleteNode(4.0);
demo.show_qx(demo.root);
System.out.println("root结点数据:"+demo.root.getValue());
}
@Test
public void testDelete(){
myTreeNodeDemo<Integer> demo = new myTreeNodeDemo<>();
TreeOperation operation = new TreeOperation();
demo.add(6);
demo.add(3);
demo.add(2);
demo.add(1);
demo.add(11);
demo.add(9);
demo.add(7);
demo.add(8);
demo.add(12);
operation.show(demo.root);
demo.deleteNode(11);
operation.show(demo.root);
}
}
4 AVL树(平衡二叉树)
4.1 描述:
- BST(二分查找树) 存在的问题是,树在插入的时候会导致倾斜,不同的插入顺序会导致树的高度不一致,而树的高度直接影响树的搜索效率。最坏的情况下所有的结点都在一条斜线上,这样树的高度为n。基于BST存在的问题,平衡二叉树(Balanced BST)产生了。平衡树的插入和删除的时候,会通过旋转操作将高度保持在logN。其中两款具有代表性的平衡树分别是AVL(高度平衡树,具备二叉搜索树的所有特性,而且左右子树的高度差不超过1) 和红黑树
- 平衡因子,某结点的左子树与右子树的高度(深度)差即为该结点的平衡因子(BF,Balance Factor)。平衡二叉树上所有结点的平衡因子只可能是 -1,0 或 1。如果某一结点的平衡因子绝对值大于1则说明此树不是平衡二叉树。
- AVL树通过插入数据时不断的左旋和右旋 来实现
public class Node<T extends Comparable<T> > implements myBaseNode {
Node parent;
Node left;
Node right;
T value;
public Node parent() {
return parent;
}
public Node left() {
return left;
}
public Node right() {
return right;
}
public T getValue() {
return value;
}
public Node(T value) {
this.value = value;
}
//从父节点删除自身,并且返回父节点
public Node removeFromParent(){
return replaceFromParent(null);
}
//从父节点处使用指定的结点替换自己
public Node replaceFromParent(Node node){
if ( parent == null ){
//基本上就是根节点
node.parent = parent ;
return parent;
}
if ( parent.left == this ){
parent.setLeft(node);
}
else{
parent.setRight(node);
}
return parent;
}
//设置左子结点,则左子结点的父节点就是this
public void setLeft(Node node){
left = node;
if ( node != null ){
node.parent = this;
}
}
//设置右子结点,则右子结点的父节点就是this
public void setRight(Node node){
right = node;
if ( node != null ){
node.parent = this;
}
}
}
package com.java.tree.AVLTree;
import com.java.tree.BalanceTree.TreeNode;
import com.java.treeShow.TreeOperation;
/**
* 描述: 平衡二叉树
* 创建时间: 2021/9/312:20
*
* @Author LDJ
* @Version v1.0
* @update [2021/9/3 12:20] [LDJ][变更描述]
**/
public class AvlTree<T extends Comparable<T>> {
Node root = null;
private Node parentOf(Node node){
if ( node == null ) return null;
return node.parent;
}
private Node leftOf(Node node){
if ( node == null ) return null;
return node.left;
}
private Node rightOf(Node node){
if ( node == null ) return null;
return node.right;
}
//插入数据
public void insert(T value){
if ( value == null ){
return;
}
if ( root == null ){
root = new Node(value);
return;
}
Node node = root;
while ( true ){
int cmp = value.compareTo((T) node.value);
if ( cmp == 0 ) return;
if ( cmp < 0 ){
//插入左边
if ( leftOf(node)==null ){
//插入位置
break;
}
else{
node = leftOf(node);
continue;
}
}
else{
if ( rightOf(node) == null ){
break;
}
else{
node = rightOf(node);
}
}
}
Node n = new Node(value);
if ( value.compareTo((T) node.value) < 0 ){
node.setLeft(n);
}
else{
node.setRight(n);
}
//
fixTree(n);
}
/**
* 每次都是检查该节点的父节点,
**/
private void fixTree(Node n) {
Node parent = parentOf(n);
while( parent != null ){
int leftHeight = maxLen(parent.left);
int rightHeight = maxLen(parent.right);
//需要旋转
if ( Math.abs(leftHeight - rightHeight)> 1) {
if ( leftHeight< rightHeight){
//左旋
ronateLeft(parent);
}
else{
//右旋
ronateRight(parent);
}
}
//向上检查
parent = parentOf(parent);
}
}
//旋转节点的 左子节点变成父节点,,
//旋转节点变为原左子结点的右节点
//原左子节点的右节点变为原旋转结点的左子节点
private void ronateRight(Node node) {
//如果是空结点或者没有左节点,不用旋转
if ( node == null || leftOf(node) == null ){
return;
}
Node leftNode = leftOf(node);
//将当前结点从父节点上摘除,并且替换成左子节点
node.replaceFromParent(leftNode);
if ( node == root){
root = leftNode;
}
Node rightNode = rightOf(leftNode);
node.setLeft(rightNode);
leftNode.setRight(node);
}
//左旋
private void ronateLeft(Node node) {
if ( node == null || rightOf(node) == null ){
return;
}
Node rightNode = rightOf(node);
node.replaceFromParent(rightNode);
if ( node == root) root = rightNode;
Node leftNode = leftOf(rightNode);
node.setRight(leftNode);
rightNode.setLeft(node);
}
private Node findNode( T value){
Node node = root;
while( node != null ){
int cmp = value.compareTo((T) node.value);
if ( cmp == 0) return node;
else if ( cmp > 0){
node = node.right;
}
else{ node = node.left;}
}
return null;
}
public void deleteNode( T value){
Node node = findNode(value);
deleteNode(node);
}
/**
* 删除结点
* 1. 如果当前删除的节点是叶子节点,直接删除
* 2. 找到前驱节点/后继节点,替换
* 1. 如果替换的节点x是叶子节点,直接 替换
* 2. 如果节点x不是叶子节点,需要找他的子结点替换节点x
*
**/
public void deleteNode(Node node){
if ( node == null){
return; //找不到就算了,不删除了
}
//叶子节点
if ( node.left() == null && node.right() == null){ //没有子节点的是叶子节点,包括单个的root结点
//直接删除
node.removeFromParent();//从parent上移除自己
}
else{
//使用前驱结点或者后继结点替代
Node nextNode = getPrecursorNode(node); //获取前驱结点(左边最大的结点->左边找右子树)
if ( nextNode == null ){
nextNode = getSuccessorNode(node); //获取后继结点(右边最小的结点->右边找左子树)
}
if ( nextNode == null ){
//找不到替换节点,
throw new RuntimeException("找不到替换节点");
}
//替换node
node.value = (nextNode.getValue());
//判断替换节点是否是叶子节点
if ( nextNode.left() !=null && nextNode.right() != null ){
//替换节点是叶子节点,不管了
nextNode.removeFromParent();
}
else
{
Node replacementNode = nextNode.left()==null?nextNode.right():nextNode.left();
//将replacementNode 替换nextNode
nextNode.replaceFromParent(replacementNode);
}
}
//删除之后需要修复平衡
fixTree(node);
}
//获取后继节点
//右子树中最小
private Node getSuccessorNode(Node node){
if ( node == null || rightOf(node) == null) return null;
Node tmpNode = rightOf(node);
while( leftOf(tmpNode) != null){
tmpNode = leftOf(tmpNode);
}
return tmpNode;
}
//获取前驱节点
//左子树最大
private Node getPrecursorNode(Node node){
if ( node == null || leftOf(node) == null) return null;
Node tmpNode = leftOf(node);
while( rightOf(tmpNode) != null){
tmpNode = rightOf(tmpNode);
}
return tmpNode;
}
//获取结点的高度
private int maxLen(Node node){
return node == null ? 0 : (1 + Math.max(maxLen(node.left()), maxLen(node.right())));
}
public static void main(String[] args) {
AvlTree<Integer> tree = new AvlTree<>();
TreeOperation operation = new TreeOperation();
for (int i = 10; i >0; i--) {
tree.insert(i);
System.out.println("----------------------"+i+"-----------------------\r\n");
operation.show(tree.root);
}
for (int i = 10; i >1; i--) {
tree.deleteNode(i);
System.out.println("----------------------"+i+"-----------------------\r\n");
operation.show(tree.root);
}
operation.show(tree.root);
}
}
5 2-3-4树
5.1 描述
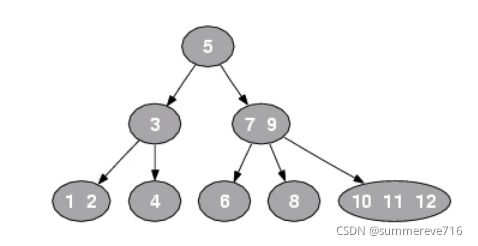
2-3-4树是四阶的B树(Balance Tree),他是属于i一种多路查找树,他的结构有以下限制
- 所有的叶子节点都有相同的深度
- 结点只能是 2结点,3结点 或者4结点之一
- 2 结点: 包括1个元素的结点,有2个子结点
- 3 结点: 包括2个元素的结点,有3个子结点
- 4 结点: 包括3个元素的结点,有4个子结点
所有的结点必须至少包括一个元素
元素始终保持排序顺序,整体上保持二叉查找树的性质,即父节点大于左子结点,小于右子结点
而且结点有多个元素时,每个元素必须大于她左边的 和 它左子树中的元素
2-3-4树的查询操作和普通二叉树一样,非常简单,但是由于其结点元素数不确定,在一些编程语言中实现并不方便,实现一般使用它的等同–红黑树
5.2 生成的过程
- 1 先插入到叶子节点(或者根节点),如果叶子节点中的元素个数小于3,则插入
- 如果叶子节点的元素超过三个,则将原叶子节点的中间的元素裂变,上移为父节点
- 上移之后还需要判断父节点是否需要裂变,,,,,
- 演示网站 (usfca.edu)
5.3 和红黑树的等价关系
红黑树起源2-3-4树,他的本质就是2-3-4树
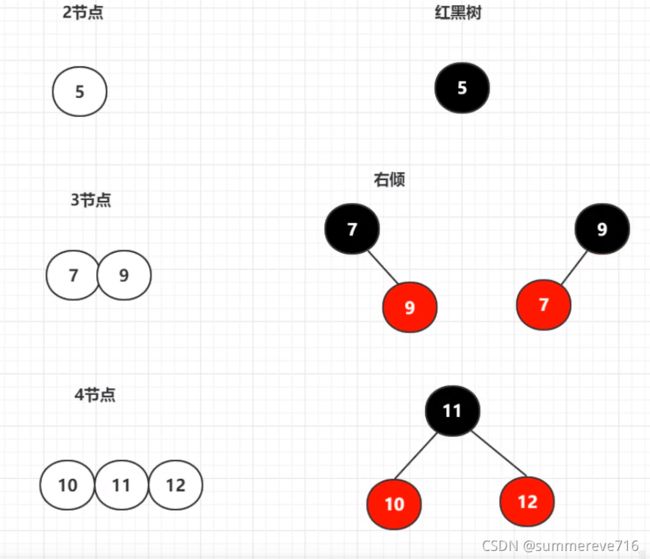
5.3.1 2结点
一个2结点对应的红黑树结点就是一个黑色节点
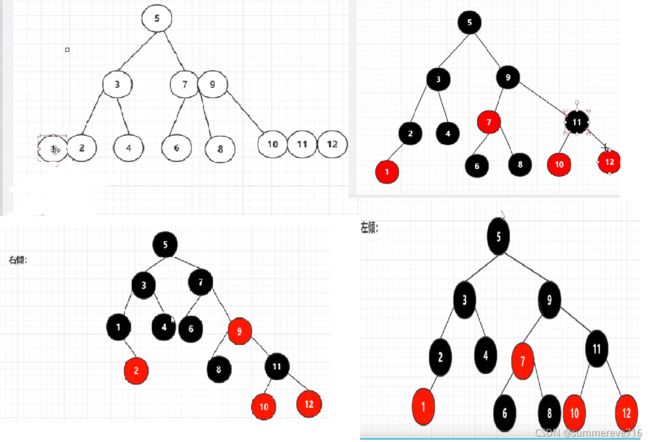
5.3.2 3结点
一个3结点可以有两种情况的红黑树结点,一种时右倾,一种时左倾。所以一个2-3-4树可以右多个红黑树
无论是左倾还是右倾,都是==上黑下红==的原则
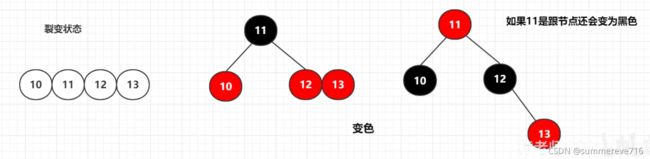
5.3.3 4结点
一个4结点对应红黑树的 ==上黑下2红==
6 红黑树
6.1描述
红黑树,Red-Black-Tree [RBT] 是一个自平衡(不是绝对的平衡)的二叉查找树[BST],树上的每个结点都遵循下面的规则:
- 每个结点要么是黑色,要么是红色
- 根节点是黑色
- 每个叶子节点(NIL)是黑色
- 每个红色结点的两个子结点一定都是黑色
- 任意一结点到每个叶子节点的路径都包含相同的黑节点
- 根据红黑树和234树的关系可知,234树的所有叶子结点的深度是一致的
- 红黑树的黑色节点是平衡的
红黑树能自平衡,靠的就是左旋,右旋和变色
操作 描述 左旋 以某个结点作为支点(旋转节点),其右子节点变为旋转节点的父节点,右子结点的左子节点变为旋转结点的右子结点,左子节点保持不变 右旋 以某个结点作为支点,其左子结点变为旋转节点的父节点,左子节点的右子节点变为旋转结点的左子节点,右子节点保持不变 变色 结点的颜色红黑转换
6.2 旋转描述
6.2.1 概念讲解
**左旋**:以某个结点作为支点(旋转节点),其右子节点变为旋转节点的父节点,右子结点的左子节点变为旋转结点的右子结点,左子节点保持不变
**右旋**:以某个结点作为支点(旋转节点),其右子节点变为旋转节点的父节点,右子结点的左子节点变为旋转结点的右子结点,左子节点保持不变
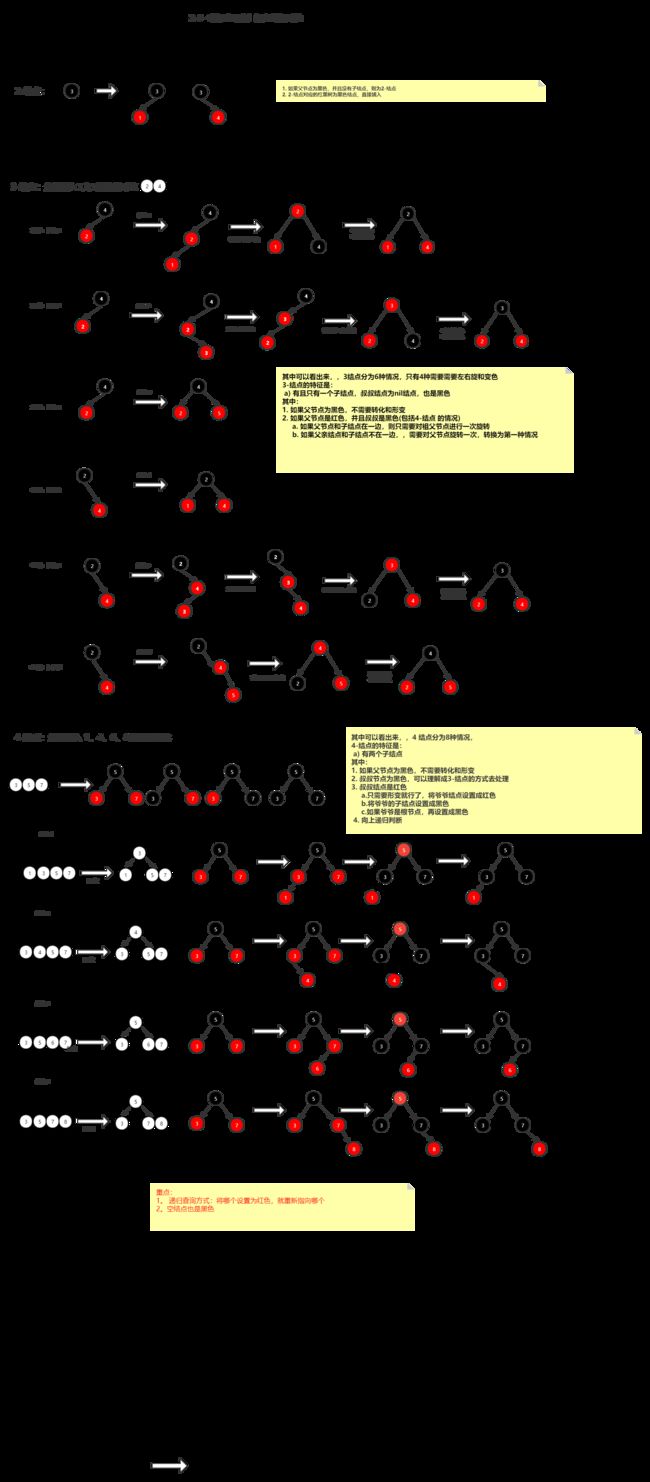
6.3 新增结点
234树中结点怎加需要遵守以下规则:
- 插入都是向最下面一层插入
- 升元: 将插入结点由 2-结点 升级成 3-结点,或 3-结点升级为4-结点
- 向4-结点插入元素之后,,需要将周昂见元素提到父节点中升元,原结点变成两个2- 结点,再把元素插入到 2-节点中,如果父节点也是4-结点,则向上递归,直到根节点后将树的高度增加1
- java面试-彻底搞懂红黑树_LYoungJ的博客-CSDN博客_java 红黑树
6.4 234树删除操作
- 情况1: 自己能搞定,对应叶子节点是3节点 和 4节点
- 情况2: 自己搞不定,需要兄弟借,但是兄弟不借,找父亲借,父亲下来,然后兄弟找一个人去代替父亲当家
- 兄弟节点是3-4-节点,
- 情况3: 找兄弟借,兄弟也没有
6.5 红黑树删除
- 遵循二叉树删除原理,对叶子节点直接删除,非叶子节点使用前驱或者后继节点替换删除
- 所以红黑树肯定是删除倒数第一层和倒数第二层
- 红黑树删除操作一定是2-3-4树的叶子节点
- 红黑树节点删除的本质就是删除2-3-4树的叶子节点,那么2-3-4树的叶子节点删除操作
代码:
package com.java.tree.RBTree;
import com.java.treeShow.myBaseNode;
/**
* 描述: []
* 创建时间: 2021/9/122:03
*
* @Author LDJ
* @Version v1.0
* @update [2021/9/1 22:03] [LDJ][变更描述]
**/
public class RBNode <K extends Comparable<K> ,V> implements myBaseNode {
public static final boolean RED = true;
public static final boolean BLACK = false;
private RBNode parent; //父节点
private RBNode left; //左子结点
private RBNode right; //右子结点
private boolean color;
private K key;
private V value;
public RBNode(RBNode parent, K key, V value) {
this.parent = parent;
this.key = key;
this.value = value;
}
public RBNode(K key, V value) {
this.key = key;
this.value = value;
}
public RBNode( K key, V value,boolean color) {
this.color = color;
this.key = key;
this.value = value;
}
public void setParent(RBNode parent) {
this.parent = parent;
}
public RBNode parent(){
return parent;
}
public RBNode left(){
return left;
}
public RBNode right(){
return right;
}
public boolean color(){
return color;
}
public void setColor(boolean color) {
this.color = color;
}
//设置左节点
public void setLeft(RBNode node){
left = node;
if ( node != null){
node.parent = this;
}
}
//设置右节点
public void setRight(RBNode node){
right = node;
if (node!= null) node.parent = this;
}
public K getKey() {
return key;
}
public V getValue() {
return value;
}
public RBNode removeFromParent(){
return replaceFromParent(null);
}
//从父节点处使用指定的结点替换自己
public RBNode replaceFromParent(RBNode node){
if ( parent == null ){
//基本上就是根节点
node.parent = parent ;
return parent;
}
if ( parent.left == this ){
parent.setLeft(node);
}
else{
parent.setRight(node);
}
return parent;
}
public void setValue(V value) {
this.value = value;
}
public void setKey(K key) {
this.key = key;
}
}
package com.java.tree.RBTree;
import com.java.treeShow.TreeOperation;
import javax.naming.ldap.Rdn;
/**
* 描述: [红黑树]
* 创建时间: 2021/9/122:01
*
* @Author LDJ
* @Version v1.0
* @update [2021/9/1 22:01] [LDJ][变更描述]
**/
public class RBTree<K extends Comparable<K>,V> {
public static final boolean RED = true;
public static final boolean BLACK = false;
//根节点
private RBNode root;
private RBNode parentOf(RBNode node){
if ( node == null ) return null;
return node.parent();
}
private RBNode leftOf(RBNode node){
if ( node == null ) return null;
return node.left();
}
private RBNode rightOf(RBNode node){
if ( node == null ) return null;
return node.right();
}
private boolean colorOf(RBNode node){
if ( node == null ) return RBNode.BLACK;
return node.color();
}
private void setColor(RBNode node ,boolean color){
if ( node == null) return;
if ( node == root ) node.setColor(RBNode.BLACK);
node.setColor(color);
}
/**
* 添加结点
* 1. 判断是否有根节点。如果没有则创建
* 2. 插入过程跟avl,二叉查找树一样,小的左边,大的右边,一样的滚蛋
* 3. 对插入结点进行判定
**/
public void add(K key,V value){
if ( key == null ){
throw new NullPointerException();
}
RBNode node = root;
if ( node == null ){
node = new RBNode(key,value);
setRoot(node);
return ;
}
RBNode newNode = new RBNode(key,value,RBNode.RED);
int cmp = 0;
while( true ){
cmp = key.compareTo((K) node.getKey()); //对比node的compare()
if ( cmp == 0 ){
return;
}
if ( cmp < 0 ){
if ( leftOf(node) == null ){
node.setLeft( newNode);
break;
}
node = leftOf(node);
continue;
}
else if ( cmp>0){
if ( rightOf(node) == null ){
node.setRight(newNode);
break;
}
node = rightOf(node);
continue;
}
}
//上面是正常的二叉树插入
fixRbTreeAfterPut(newNode);
}
/**
* 对插入结点进行判断 是否需要旋转或者变色 ,
* 把 哪个设置成红色,就把x指向哪个
* 还有就是黑色结点和空结点一样,都是黑色,,所以,,反过来,可以把
* 归纳 :
* 2-结点本身就是黑色,且没有子节点,则直接插入
* 3-结点有一个非空子结点,
* 4-结点有两个非空,当两个子结点为一红一黑时,可以当作3-结点处理
* 逻辑判断
* 1.如果当前结点是null,则直接返回
* 2.如果当前结点的父节点是黑色,则直接返回,不需要处理
* 3.如果叔叔节点为红色,则是4-结点,
* a.将爷爷节点设置成红色
* b.将父节点和叔叔节点设置成黑色
* c.需要判定爷爷节点是否为根节点,如果是,则设置为黑色,并且退出循环
* d.如果不是root则指向爷爷,然后继续循环
* 4.叔叔结点为黑色,全部归纳为3-结点处理,(此时父亲是红色,自己也是红色)
* 4.1. 如果父亲在左侧
* 4.1.1 如果自己在左侧,将爷爷节点右旋,然后将父亲设置为黑色,父亲的右节点设置为红色
* 4.1.2 如果自己在右侧,将父节点右旋,再将自己指向左节点,就变成和4.1.1一样的情况
* 4.2. 如果父亲在右侧
* 4.2.1 如果自己在右侧,将爷爷节点左旋,然后将原父亲设置为黑色,原父亲的左节点设置为红色
* 4.2.2 如果自己在右侧,将父节点左旋,再将自己指向右节点,就变成和4.2.1一样的情况
**/
private void fixRbTreeAfterPut(RBNode x) {
if ( x == null )
{
//如果 结点x == null则直接返回
return ;
}
setColor(x,RED);
while ( x != null && x!= root && colorOf(parentOf(x))==RED){
//通过判断是否有叔叔结点来确定是3结点还是4结点
RBNode uncleNode = leftOf(parentOf(parentOf(x))) == parentOf(x)? rightOf(parentOf(parentOf(x))): leftOf(parentOf(parentOf(x)));
if ( colorOf(uncleNode) == BLACK) {
//如果父亲在左侧
if ( parentOf(x) == leftOf(parentOf(parentOf(x)))){
//4.1.1 如果自己在左侧,将爷爷节点右旋,然后将父亲设置为黑色,父亲的右节点设置为红色
if ( x == leftOf( parentOf(x))){
rotateRight(parentOf(parentOf(x)));
setColor(parentOf(x),BLACK);
setColor(rightOf(parentOf(x)),RED);
x = parentOf(x);
}
else{
//4.1.2 如果自己在右侧,将父节点右旋,再将自己指向左节点,就变成和4.1.1一样的情况
rotateLeft(parentOf(x));
x = leftOf(x);
}
}
else{
if ( x == rightOf(parentOf(x))){
//4.2.1 如果自己在右侧,将爷爷节点左旋,然后将原父亲设置为黑色,原父亲的左节点设置为红色
rotateLeft(parentOf(parentOf(x)));
setColor(parentOf(x),BLACK);
setColor(leftOf(parentOf(x)),RED);
x = parentOf(x);
}
else{
//4.2.2 如果自己在右侧,将父节点左旋,再将自己指向右节点,就变成和4.2.1一样的情况
rotateRight(parentOf(x));
x = rightOf(x);
}
}
}
else
{
// 3.如果叔叔节点为红色,则是4-结点,
//a.将爷爷节点设置成红色
setColor(parentOf(parentOf(x)),RED);
// b.将父节点和叔叔节点设置成黑色
setColor(leftOf(parentOf(parentOf(x))),BLACK);
setColor(rightOf(parentOf(parentOf(x))),BLACK);
//c.需要判定爷爷节点是否为根节点,如果是,则设置为黑色,并且退出循环
if ( parentOf(parentOf(x)) == root){
setRoot(parentOf(parentOf(x)));
return;
}
else{
//d.如果不是root则指向爷爷,然后继续循环
x = parentOf(parentOf(x));
}
}
}
if ( x!= null && x == root ){
setRoot(x);
}
}
/**
* 根据key删除节点
* @author : LDJ
* @date : 2021/9/7 10:55
* @param key
* @return 类型:V 说明:
**/
public V removeValue(K key){
RBNode node = find(key);
//没找到
if ( node == null )return null;
return removeNode2(node);
}
/**
* 根据key找到对应的节点
* @author : LDJ
* @date : 2021/9/7 10:57
* @param key
* @return 类型:com.java.tree.RBTree.RBNode 说明:
**/
private RBNode find(K key){
RBNode node = root;
while( node!= null ){
int cmp = key.compareTo((K) node.getKey());
if ( cmp == 0 )return node;
else if ( cmp > 0 ) node =node.right();
else node = node.left();
}
return null;
}
/**
* 删除节点
* 1. 如果当前节点是空结点,直接返回null
* 2. 如果当前节点是叶子节点,直接删除
* 3. 获取前驱节点,也就是替换节点,然后获取不到就获取后继节点
* 4. 将前驱节点的key和value赋值给node,
* 5. 将precursorNode 的子结点替换precursorNode 的位置
* 6. 将precursorNode从其父类中删除
**/
private V removeNode( RBNode node){
//三种情况
if ( node == null )return null;
V oldValue = (V) node.getValue();
//如果是叶子节点
if ( leftOf(node)== null && rightOf(node) == null ){
if ( node==root){
root = null;
}
else{
//如果不是root节点
//可能还需要判断删除的节点是什么颜色,如果是红色,不用管,
//如果是黑色,破坏了红黑树的平衡,还需要修复
if ( colorOf(node) == BLACK ){
fixRbTreeAfterRemove(node);
}
node.removeFromParent();
}
}
else{
//获取前驱节点,也就是替换节点
RBNode replacementNode = getSuccessorNode(node);
if ( replacementNode == null ){
replacementNode = getSuccessorNode(node);
}
//没有前驱也没有后置节点,只能说明是叶子节点,上面处理过,如果还出现,肯定是出问题了
if ( replacementNode == null ){
throw new RuntimeException("not found replacement node");
}
//替换节点数据
node.setKey(replacementNode.getKey());
node.setValue(replacementNode.getValue());
//然后判断replacementNode节点的数据
//是否有子结点,如果有,则将其替换到原replacementNode的位置
//而且最多只有一个节点
RBNode childNode = replacementNode.left()==null?replacementNode.right():replacementNode.left();
if ( childNode!= null){
//存在一个节点
//将childNode 在replacementNode 的父节点上替换掉replacementNode
replacementNode.replaceFromParent(childNode);
}
else{
replacementNode.removeFromParent();
}
//删除的是前驱节点,所以要啊判断一下前驱节点的颜色
if ( colorOf(childNode) == BLACK ){
fixRbTreeAfterRemove(childNode);
}
//置空
replacementNode = null;
}
return oldValue;
}
/**
* 删除节点:
* 1. 如果node是非叶子节点,找到要删除节点的前驱或者后继节点 nextNode
* 2. 将nextNode的数据赋给node,然后将node指向nextNode,从而将删除node变为删除nextNode
* 3. 如果nextNode 是叶子节点,则先判断是否为黑色,如果是黑色先形变,然后再删除
* 4. 如果不是叶子节点,获取他的子结点,替换nextNode的位置,然后判断nextNode是否黑色,如果是则形变子结点
**/
private V removeNode2( RBNode node){
if( node == null )return null;
V oldValue = (V) node.getValue();
//非叶子节点
if ( leftOf(node) != null || rightOf(node)!=null){
RBNode replaceNode = getPrecursorNode(node);
if ( replaceNode == null ){
replaceNode = getSuccessorNode(node);
}
node.setValue(replaceNode.getValue());
node.setKey(replaceNode.getKey());
//然后就变成了删除 前驱或者后继节点
node = replaceNode;
}
//将问题变为删除nextNode
//此时,只需要判定,是叶子节点,还是有一个节点的情况
//获取子结点,如果存在就是非叶子节点,如果不存在,就是叶子节点
RBNode replaceNode = leftOf(node)==null ? rightOf(node):leftOf(node);
if ( replaceNode == null ){
//叶子节点
//先判定是否为黑色 直接删除
if ( colorOf(node) == BLACK){
fixRbTreeAfterRemove(node);
}
//直接删除
node.removeFromParent();
}
else{
//如果是非叶子节点,存在一个替换节点
//将replaceNode 替换到node的父节点位置
node.replaceFromParent(replaceNode);
//因为node是要删除的,replaceNode只是移到了node的位置
if ( colorOf(node) == BLACK){
fixRbTreeAfterRemove(replaceNode);
}
node = null;
}
return oldValue;
}
/**
* 删除了一个红黑节点之后,进行修复,有点复杂,分为三种情况:
* 情况一:自己能搞对,自己所在的是3-节点或4-节点
* 情况二:自己搞不定,父亲下来,兄弟中找一个去当爸爸。。兄弟是3-节点或者4-节点
* 情况三:自己和兄弟都搞不定
**/
private void fixRbTreeAfterRemove(RBNode x) {
/**
* 如果是红色节点,已经直接删除了,所以不可能出现,也就是说,形变的情况,只需要考虑情况二 和情况三
* 而这两种情况下都需要向兄弟借,因此,需要先获取到兄弟。
* 在获取到兄弟之后,判断兄弟的类型从而确定是情况二还是情况三
* 重点:获取真正的兄弟节点,需要配合2-3-4树来看
* 如果兄弟是 叶子节点,则是情况三
* 如果兄弟是 3-节点或者4-节点,则是情况二
*/
while ( x != null && x != root && colorOf(x)==BLACK){
//先从左边判断
//为什么不讨论没有兄弟的情况呢?因为红黑树是黑色平衡树,不可能存在父亲是黑色,而没有叔叔的情况
if ( x == leftOf(parentOf(x))){
//自己在父节点的左边
RBNode broNode = rightOf(parentOf(x));
//这是兄弟节点,需要判断是否是真的兄弟节点
//判断依据就是,bronode不是红色,黑色是真兄弟,红色是假的
//需要进行形变,具体方式是将2-3-4树的左倾换成右倾
if ( colorOf(broNode) == RED ){
//切换左右倾,先变色
//父节点和兄弟节点互换颜色,然后父节点左倾
setColor(parentOf(x),RED);
setColor(broNode,BLACK);
rotateLeft(parentOf(x));
//重新获取兄弟节点
broNode = rightOf(parentOf(x));
}
//然后就是判断情况二还是情况三 ,
//情况二 兄弟节点至少有一个红色,,情况三 兄弟的节点都是黑色
if ( colorOf(leftOf(broNode)) == BLACK && colorOf(rightOf(broNode)) == BLACK){
//这是情况三
//有两种情况,一种是父节点红色,兄弟节点黑色,只需要将兄弟节点变红,然后向上递归就行
//第二种情况,父节点黑色,兄弟黑色,删除节点会破坏平衡
//暂时有点问题
setColor(broNode,RED);
x = parentOf(x);
}
else{
//这是情况二=
//如果兄弟节点的子结点在右边
if ( colorOf(rightOf(broNode)) == BLACK){
setColor(broNode,RED);
setColor(leftOf(broNode),BLACK);
rotateLeft(broNode);
//重新获取兄弟节点
broNode = rightOf(parentOf(x));
}
setColor(broNode,colorOf(parentOf(x)));
setColor(parentOf(x),BLACK);
setColor(rightOf(broNode),BLACK);
rotateLeft(parentOf(x));
x = root;
}
}
else{
RBNode broNode = leftOf(parentOf(x));
//这是兄弟节点,需要判断是否是真的兄弟节点
//判断依据就是,bronode不是红色,黑色是真兄弟,红色是假的
//需要进行形变,具体方式是将2-3-4树的左倾换成右倾
if ( colorOf(broNode) == RED ){
//切换左右倾,先变色
//父节点和兄弟节点互换颜色,然后父节点左倾
setColor(broNode,BLACK);
setColor(parentOf(x),RED);
rotateRight(parentOf(x));
//重新获取兄弟节点
broNode = leftOf(parentOf(x));
}
//然后就是判断情况二还是情况三 ,
//情况二 兄弟节点至少有一个红色,,情况三 兄弟的节点都是黑色
if ( colorOf(leftOf(broNode)) == BLACK && colorOf(rightOf(broNode)) == BLACK){
//这是情况三
//有两种情况,一种是父节点红色,兄弟节点黑色,只需要将兄弟节点变红,然后向上递归就行
//第二种情况,父节点黑色,兄弟黑色,删除节点会破坏平衡
//暂时有点问题
setColor(broNode,RED);
x = parentOf(x);
}
else{
//这是情况二
//如果兄弟节点的子结点在右边
if ( colorOf(leftOf(broNode)) == BLACK){
setColor(broNode,RED);
setColor(rightOf(broNode),BLACK);
rotateRight(broNode);
//重新获取兄弟节点
broNode = leftOf(parentOf(x));
}
setColor(broNode,colorOf(parentOf(x)));
setColor(parentOf(x),BLACK);
setColor(leftOf(broNode),BLACK);
rotateRight(parentOf(x));
x = root;
}
}
}
setColor(x,RBNode.BLACK);
}
//设置根节点
public void setRoot(final RBNode node){
node.setColor(RBNode.BLACK);
this.root = node;
}
//左旋
/*
1. 判断旋转结点是否为空,如果为空则直接退出
2. 判断旋转结点是否有右子节点,如果没有则直接退出
3. 在旋转结点的父结点处,将原旋转节点替换成右子节点,如果原旋转节点为根节点,则设置原右子节点为根节点
4. 先缓存原右子节点的左子节点,将原旋转结点设置成原右子节点的左子结点,
5. 将第四步保存的原右子节点的左子结点插入到原旋转节点的右子节点
6. 完成左旋
*/
private void rotateLeft(RBNode node){
//1. 判断当前结点是否为空,
if ( node == null ){
return;
}
//2 .判断当前结点是否右右子节点
//右子节点为空,则不能旋转
RBNode rightNode = rightOf(node);
if ( rightNode == null ){
return ;
}
//3.在旋转结点的父结点处,将原旋转节点替换成右子节点,如果原旋转节点为根节点,则设置原右子节点为根节点
node.replaceFromParent(rightNode);
if ( node == root){
//根节点
setRoot(rightNode);
}
//4.将原旋转结点设置成原右子节点的左子结点
RBNode leftNode = leftOf(rightNode);
rightNode.setLeft(node);
//5.最后将原右子节点的左子结点插入到 原旋转节点的右子节点
node.setRight(leftNode);
//打完收工
}
/*
1. 判断旋转结点是否为空,如果为空则直接退出
2. 判断旋转结点是否有左子节点,如果没有则直接退出
3. 在旋转结点的父结点处,将原旋转节点替换成左子节点,如果原旋转节点为根节点,则设置原左子节点为根节点
4. 先缓存原右子节点的右子节点,将原旋转结点设置成原左子节点的右子结点,
5. 将第四步保存的原左子节点的右子结点插入到原旋转节点的左子节点
6. 完成右旋
*/
private void rotateRight(RBNode node){
//1. 判断旋转结点是否为空,如果为空则直接退出
if ( node == null ) return;
//2. 判断旋转结点是否有左子节点,如果没有则直接退出
RBNode leftNode = leftOf(node);
if ( leftNode == null ) return;
//3. 在旋转结点的父结点处,将原旋转节点替换成左子节点,如果原旋转节点为根节点,则设置原左子节点为根节点
node.replaceFromParent(leftNode);
if ( node == root ){
setRoot(leftNode);
}
//4. 先缓存原右子节点的右子节点,将原旋转结点设置成原左子节点的右子结点,
RBNode rightNode = rightOf(leftNode);
leftNode.setRight(node);
//5. 将第四步保存的原左子节点的右子结点插入到原旋转节点的左子节点
node.setLeft(rightNode);
}
/**
* 获取前驱结点
* 1. 如果当前结点有左子节点,则遍历左子节点的右树,最大值就是前驱节点
* 2. 如果没有左子节点:
* 2.1 若该节点是其父节点的右边孩子,那么该节点的前驱结点即为其父节点。
* 2.2 若该节点是其父节点的左边孩子,那么需要沿着其父亲节点一直向树的顶端寻找
**/
private RBNode getPrecursorNode(RBNode node){
if ( node == null ){
throw new NullPointerException();
}
if ( leftOf(node) == null ){
RBNode p = node.parent();
RBNode tm = node;
while ( p != null && p.left() == tm ){
tm = p;
p = tm.parent();
}
return p;
}
else{
RBNode precursorNode = leftOf(node);
while( true){
if ( rightOf(precursorNode) == null){
break;
}
precursorNode = rightOf(precursorNode);
}
return precursorNode;
}
}
/**
* 获取后继节点
* 1. 如果当前结点有 [右子节点],则遍历 [右子节点]的 [左树],最小值就是后继节点
* 2. 如果没有 [右子节点]:
* 2.1 若该节点是其父节点的左边孩子,那么该节点的后继结点即为其父节点。
* 2.2 若该节点是其父节点的右边孩子,那么需要沿着其父亲节点一直向树的顶端寻找
*/
private RBNode getSuccessorNode(RBNode node){
if ( node == null ){
throw new NullPointerException();
}
if ( rightOf(node) == null ) {
RBNode p = node.parent();
RBNode tm = node;
while ( p != null && p.right() == tm ){
tm = p;
p = tm.parent();
}
return p;
}
else{
RBNode successorNode = rightOf(node);
while ( true ){
if ( leftOf(successorNode) == null){
break;
}
successorNode = leftOf(successorNode);
}
return successorNode;
}
}
//遍历
public void showQX(final RBNode node ){
if ( node == null) return;
System.out.println(node.getKey());
showQX(leftOf(node));
showQX(rightOf(node));
}
public static void main(String[] args) {
RBTree<Integer,String> tree = new RBTree<>();
TreeOperation operation = new TreeOperation();
final String value = "demo";
final int array[] = {6,4,8,3,5,7,9,1,2,10};
for (int i = 1; i < 11; i++) {
tree.add(i,value);
operation.show(tree.root);
System.out.println("---------------------"+i+"----------------------");
}
tree.removeValue(5);
operation.show(tree.root);
}
}
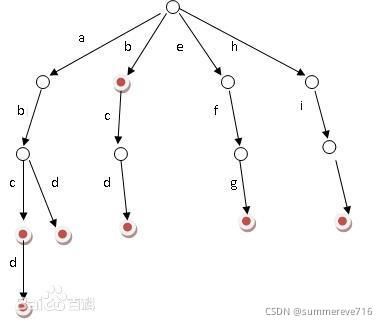
7 Trie树
说明:又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
性质
packagecom.suning.search.test.tree.trie;
public class Trie
{
private int SIZE=26;
private TrieNode root;//字典树的根
Trie() //初始化字典树
{
root=new TrieNode();
}
private class TrieNode //字典树节点
{
private int num;//有多少单词通过这个节点,即由根至该节点组成的字符串模式出现的次数
private TrieNode[] son;//所有的儿子节点
private boolean isEnd;//是不是最后一个节点
private char val;//节点的值
private boolean haveSon;
TrieNode()
{
num=1;
son=new TrieNode[SIZE];
isEnd=false;
haveSon=false;
}
}
//建立字典树
public void insert(String str) //在字典树中插入一个单词
{
if(str==null||str.length()==0)
{
return;
}
TrieNode node=root;
char[]letters=str.toCharArray();
for(int i=0,len=str.length(); i<len; i++)
{
int pos=letters[i]-'a';
if(node.son[pos]==null)
{
node.haveSon = true;
node.son[pos]=newTrieNode();
node.son[pos].val=letters[i];
}
else
{
node.son[pos].num++;
}
node=node.son[pos];
}
node.isEnd=true;
}
//计算单词前缀的数量
public int countPrefix(Stringprefix)
{
if(prefix==null||prefix.length()==0)
{
return-1;
}
TrieNode node=root;
char[]letters=prefix.toCharArray();
for(inti=0,len=prefix.length(); i<len; i++)
{
int pos=letters[i]-'a';
if(node.son[pos]==null)
{
return 0;
}
else
{
node=node.son[pos];
}
}
return node.num;
}
//打印指定前缀的单词
public String hasPrefix(String prefix)
{
if (prefix == null || prefix.length() == 0)
{
return null;
}
TrieNode node = root;
char[] letters = prefix.toCharArray();
for (int i = 0, len = prefix.length(); i < len; i++)
{
int pos = letters[i] - 'a';
if (node.son[pos] == null)
{
return null;
}
else
{
node = node.son[pos];
}
}
preTraverse(node, prefix);
return null;
}
// 遍历经过此节点的单词.
public void preTraverse(TrieNode node, String prefix)
{
if (node.haveSon)
{
for (TrieNode child : node.son)
{
if (child!=null)
{
preTraverse(child, prefix+child.val);
}
}
return;
}
System.out.println(prefix);
}
//在字典树中查找一个完全匹配的单词.
public boolean has(Stringstr)
{
if(str==null||str.length()==0)
{
return false;
}
TrieNode node=root;
char[]letters=str.toCharArray();
for(inti=0,len=str.length(); i<len; i++)
{
intpos=letters[i]-'a';
if(node.son[pos]!=null)
{
node=node.son[pos];
}
else
{
return false;
}
}
return node.isEnd;
}
//前序遍历字典树.
public void preTraverse(TrieNodenode)
{
if(node!=null)
{
System.out.print(node.val+"-");
for(TrieNodechild:node.son)
{
preTraverse(child);
}
}
}
public TrieNode getRoot()
{
return this.root;
}
public static void main(String[]args)
{
Trietree=newTrie();
String[]strs= {"banana","band","bee","absolute","acm",};
String[]prefix= {"ba","b","band","abc",};
for(Stringstr:strs)
{
tree.insert(str);
}
System.out.println(tree.has("abc"));
tree.preTraverse(tree.getRoot());
System.out.println();
//tree.printAllWords();
for(Stringpre:prefix)
{
int num=tree.countPrefix(pre);
System.out.println(pre+""+num);
}
}
}