机器学习3——朴素贝叶斯（基于概率论的分类方法）

贝叶斯公式

条件概率

• 事件（结果）：A
• 原因（条件）：B

公式：
$$P(B|A)=\frac{P(AB)}{P(A)}$$
变形：
$$P(AB)=P(B|A)P(A)=P(A|B)P(B)$$
多事件的条件概率公式：
$$P(A_1{A}_2{A}_3{A}_4{A}_5)=P(A_1)P(A_2|A_1)P(A_3|A_1{A}_2)P(A_4|A_1{A}_2{A}_3)P(A_5|A_1{A}_2{A}_3{A}_4)$$

全概率公式

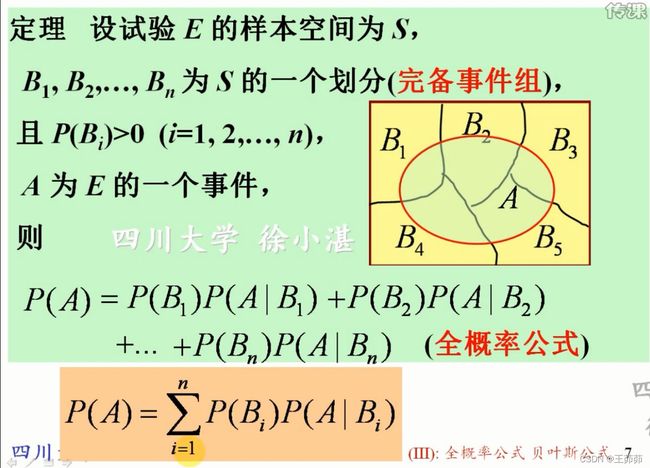
全概率公式的推导：

全概率公式的意义：
由原因推结果。事件A发生的概率是由所有可能导致事件A发生的原因的概率的总和。

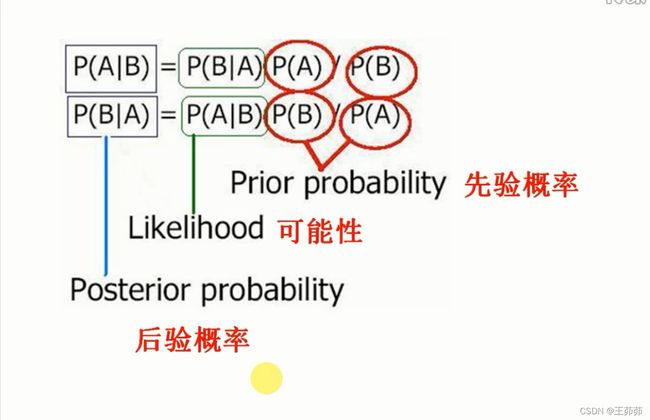
贝叶斯公式

贝叶斯公式：
$$P(B_i|A)=\frac{P(A|B_i)P(B_i)}{P(A)}$$
公式推导：

公式意义：
事件A已经发生的条件下，求解导致事件A发生的原因B_i的概率。

先验概率、后验概率

该部分参考链接
频率流派和贝叶斯流派的解读

朴素贝叶斯

参考链接：给出了朴素贝叶斯算法非常简洁明了的例子解释
贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而朴素朴素贝叶斯分类是贝叶斯分类中最简单，也是常见的一种分类方法。

朴素： 朴素贝叶斯算法是假设各个特征之间相互独立

贝叶斯分类的基本思想就是根据贝叶斯公式求解给定数据（特征）属于某个类别的概率，选择概率最大的类别作为数据的最终类别。

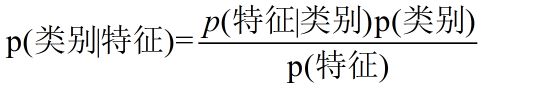
例子:
给定一个人的特征为（不帅、性格不好、身高矮、不上进），还有一系列的数据（训练集），希望求得对于这个人是选择嫁还是不嫁（就是对这个人进行分类）。

根据朴素贝叶斯的分类思想，分别求得 P（嫁|不帅、性格不好、身高矮、不上进）与P（不嫁|不帅、性格不好、身高矮、不上进）的值，最大的即为该人的类别。

朴素贝叶斯模型优缺点

• 优点：
  在数据较少的情况下仍然适用，可以处理多类别问题。
• 缺点：
  对于输入数据的类型要求比较高，需要的是标称型数据。因此对于数值型的数据可能需要划分范围进行处理等。

使用朴素贝叶斯过滤垃圾邮件

根据朴素贝叶斯算法对邮件进行分类，二分类问题。

实现步骤：
1、准备数据：
将文本数据解析成词条向量。

• 先读入文本内容；
• 然后对文本内容进行切分，切分成一个词语的List，此处使用正则表达式进行筛选，去掉无用的标点符号；textParse(String)
• 创建一个list存放数据集中出现的所有的单词，构成词袋；createVocabList(dataSet)
• 根据词袋计算每个文本的词向量，在该示例中使用0-1向量表示；setOfWords2Vec(vocabList, input)

2、训练算法：trainNB(trainMatrix, trainCategory)
对于朴素贝叶斯模型，对算法的训练其实就是根据训练集的数据计算公式需要的先验概率以及条件概率。注意，为了避免出现小数相乘下溢的现象，代码中使用log函数进行计算。（重点看看对于下溢问题的处理

• 计算每个类别在数据集中出现的频率（频率表示概率）；
• 计算每个类别下所有的训练集数据中每个词的出现的次数，以及该类别下的所有训练数据集的所有的词的出现次数。
  （因为使用的是0-1向量表示文本数据，因此可以直接对训练集的所有向量进行相加即可计算每个词出现的次数）

3、测试算法：classifyNB(vec2Classify, p0Vec, p1Vec, pClass1)
根据训练函数计算的先验概率以及条件概率，计算每个类别下的测试数据的后验概率，选择后验概率最大的类别作为最终的类别。

import random

import numpy as np
from math import log


def loadDataSet():
    postingList = [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                   ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                   ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                   ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                   ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                   ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0, 1, 0, 1, 0, 1]  # 1 is abusive, 0 not
    return postingList, classVec


def createVocabList(dataSet):
    # 创建一个list存放数据集中出现的所有的单词
    vocabList = set([])  # 使用set来保证集合元素的不重复性
    for data in dataSet:
        vocabList |= set(data)  # 求并集
    return list(vocabList)


def setOfWords2Vec(vocabList, input):
    '''
    将input输入转换为词汇向量，在input中出现的词汇标注为1，其余为0
    :param vocabList:
    :param input:
    :return:
    '''
    inputVec = [0] * len(vocabList)
    for word in set(input):
        if word in vocabList:
            index = vocabList.index(word)
            inputVec[index] = 1
        else:
            print("%s在词汇表中没有出现过" % (word))
    return inputVec


def bagOfWords2Vec(vocabList, input):
    '''
    将句子转化为词向量，但是对于出现的词使用其出现次数表示
    :param vocabList:
    :param input:
    :return:
    '''
    inputVec = [0] * len(vocabList)
    for word in set(input):
        if word in vocabList:
            index = vocabList.index(word)
            inputVec[index] += 1
        else:
            print("%s在词汇表中没有出现过" % (word))
    return inputVec


def trainNB(trainMatrix, trainCategory):
    '''
    二分类问题，计算贝叶斯公式中需要的部分，先验概率【二分类所以只计算一种类别的概率即可，另一种直接 1-】以及条件概率【对文档的词向量计算每个类别的条件概率，返回向量】
    :param trainMatrix: 训练集的文档矩阵,每一行是【0,1】vector（词向量）
    :param trainCategory: 训练集的类别向量
    :return:
    '''
    numTrainDoc = len(trainMatrix)
    numWords = len(trainMatrix[0])
    # 1、先计算每个类别的先验概率P(C_i)
    cate1P = sum(trainCategory) / float(numTrainDoc)
    # 2、计算条件概率
    # 先计算每个类别下，每个单词在文档矩阵中出现的频次
    wordFreq0 = np.ones(numWords)  # 此处初始化为1，防止出现条件概率为0的项导致计算乘积之后整个分子都变0
    wordFreq1 = np.ones(numWords)
    cateWords0 = 2.0  # 此处初始化为2
    cateWords1 = 2.0
    for docindex in range(numTrainDoc):
        if trainCategory[docindex] == 0:
            wordFreq0 += trainMatrix[docindex]  # 此处很巧妙，trainMatrix是词向量【0-1向量】构成的，因此只需+即可
            cateWords0 += sum(trainMatrix[docindex])
        else:
            wordFreq1 += trainMatrix[docindex]
            cateWords1 += sum(trainMatrix[docindex])
    wordFreq0 = np.log(wordFreq0 / cateWords0)  # 为了防止小数相乘导致的下溢，所以使用log函数
    wordFreq1 = np.log(wordFreq1 / cateWords1)
    return wordFreq0, wordFreq1, cate1P


def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    '''
    朴素贝叶斯分类函数，只需要计算每个类别的后验概率，选择最大的类别即可
    :param vec2Classify: 待分类的词向量
    :param p0Vec:
    :param p1Vec:
    :param pClass1:
    :return:
    '''
    p0 = sum(vec2Classify * p0Vec) + log(1 - pClass1)  # 注意啊，此处，因为已经将结果转化为了log，所以原来的乘法---变成了加法
    p1 = sum(vec2Classify * p1Vec) + log(pClass1)
    if p0 > p1:
        return 0
    else:
        return 1


def textParse(String):
    '''
    解析句子。将句子解析为单词列表。去掉其中的标点符号并且将所有的字符转为小写。
    :param String:
    :return:
    '''
    import re
    listOfTokens = re.split(r'\W*', String)  # re.split(pattern,str)根据pattern进行切分
    return [word.lower() for word in listOfTokens if len(word) > 2]


def spamTest():
    '''
    对贝叶斯垃圾邮件分类器进行实现
    :return:
    '''
    # 1、首先读入数据，并且解析文本文件
    docList = []
    classList = []
    # docWordsList = []
    for i in range(1, 26):
        doc = textParse(open('./email/spam/%d.txt' % i).read())
        docList.append(doc)
        # docWordsList.extend(doc)
        classList.append(1)
        doc = textParse(open('./email/ham/%d.txt' % i).read())
        docList.append(doc)
        # docWordsList.extend(doc)
        classList.append(0)
    # 2、随机构建测试集以及训练集
    vocabList = createVocabList(docList)
    testSet = []  # 随机选择10例作为测试集
    trainSet = list(range(50))
    for i in range(10):
        randomnum = int(random.uniform(0,50))
        print(randomnum)
        testSet.append(randomnum)
        del (trainSet[randomnum])
    # 3、训练：将选定的训练集的数据转化为词向量然后输入到trainNB函数中计算先验概率以及条件概率
    trainMatrix = []
    trainClass = []
    for docindex in trainSet:
        trainMatrix.append(setOfWords2Vec(vocabList, docList[docindex]))
        trainClass.append(classList[docindex])
    wordFreq0, wordFreq1, cate1P = trainNB(np.array(trainMatrix), np.array(trainClass))
    # 4、测试：计算错误率
    errorcount = 0
    for docindex in testSet:
        docVector = setOfWords2Vec(vocabList, docList[docindex])
        res = classifyNB(docVector, wordFreq0, wordFreq1, cate1P)
        if res != classList[docindex]:
            errorcount += 1
    print("错误率是", errorcount / float(len(testSet)))


# 按间距中的绿色按钮以运行脚本。
if __name__ == '__main__':
    dataSet, labels = loadDataSet()
    vocabList = createVocabList(dataSet)
    print(vocabList)

    # instanceVec = setOfWords2Vec(vocabList, dataSet[0])
    # print(instanceVec)

    dataMatrix = []
    for doc in dataSet:
        dataMatrix.append(setOfWords2Vec(vocabList, doc))
    wordFreq0, wordFreq1, cateP1 = trainNB(dataMatrix, labels)
    print(wordFreq0)
    print(wordFreq1)
    print(cateP1)

    # testNB
    testDoc1 = testEntry = ['love', 'my', 'dalmation']
    testVec1 = np.array(setOfWords2Vec(vocabList, testDoc1))
    print(classifyNB(testVec1, wordFreq0, wordFreq1, cateP1))

    testDoc2 = ['stupid', 'garbage']
    testVec2 = np.array(setOfWords2Vec(vocabList, testDoc2))
    print(classifyNB(testVec2, wordFreq0, wordFreq1, cateP1))

    spamTest()