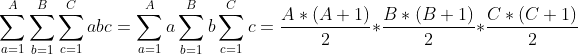AtCoder题解——AtCoder Regular Contest 107——A - Simple Math

题目相关

题目链接

AtCoder Regular Contest 107 A 题，https://atcoder.jp/contests/arc107/tasks/arc107_a。

Problem Statement

Given are three positive integers A, B, and C. Compute the following value modulo 998244353：

Input

Input is given from Standard Input in the following format:

A B C

Output

Print the value modulo 998244353.

Samples1

Sample Input 1

1 2 3

Sample Output 1

18

Explaination

We have: (1×1×1)+(1×1×2)+(1×1×3)+(1×2×1)+(1×2×2)+(1×2×3)=1+2+3+2+4+6=18.

Samples2

Sample Input 2

1000000000 987654321 123456789

Sample Output 2

951633476

Constraints

• 1 ≤ A, B, C ≤ 10^9

题解报告

题目翻译

给定三个正数 A、B 和 C，求 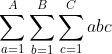的值，数据要对 998244353 取模。

题目分析

一个标准的数论题目，不要被三个累计求和吓住了。如果使用暴力，由于最大值是 10^9，这样最大的计算可能性就是 10^9*10^9*10^9=10^27，肯定是 TLE。

我们知道等差数列求和公式为：

公式中首项为 ，项数为 n，公差为 d，前 n 项和为 Sn。

对于本题公差为 1 的等差数列，。

这样，我们可以将计算公式进行化简：

这样，我们通过数学方法，将 复杂度变为 O(1)。

数据范围估计

根据题目描述，，这样 的最大值为 ，可以使用 long long 表示。

同余定理

本题的考点之一。

对于乘法而言：(a*b) mod c = ((a mod c) * (b mod c)) mod c。

AC 参考代码

//https://atcoder.jp/contests/arc107/tasks/arc107_a
//A - Simple Math Editorial

#include 

using namespace std;

const long long MO=998244353;
int main() {
    long long a,b,c;
    cin>>a>>b>>c;

    long long t0=(a*(a+1)/2)%MO;
    long long t1=(b*(b+1)/2)%MO;
    long long t2=(c*(c+1)/2)%MO;
    long long ans=(t0*t1)%MO;
    ans=(ans*t2)%MO;
    cout<