KMP 算法 + 运用前后缀信息 + 案例分析 + 实战力扣题

一、理解KMP算法如何运用后缀和前缀的信息

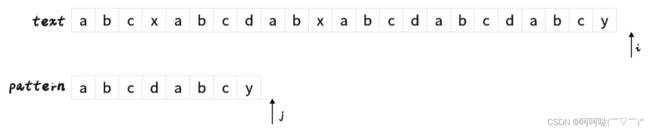
• 文本串text:abcxabcdabxabcdabcdabcy
• 模式串pattern:abcdabcy

当发现不匹配的点，我们的目标不是在这个串中进行回溯操作。因此我们要检查的是 d 的前面的子串（abc），在这个子串（abc）中是否存在后缀与前缀相同的情况。所有的字符都是单独的，因此这里没有后缀与前缀相同的情况，因此意味着我们下一个比较对象将从 x 和 a 开始，再一次地，我们将会理解得更好在这个例子当中。

此时发现还是匹配失败，而 j = 0,退无可退了，那么就 i++；（指向下一个位置）

匹配成功的话就 i++; j++;

当 i 指向 x ，j 指向 c 的时候，发生匹配失败！因此再一次地，我们检查在 c 前面的子串（abcdab）中，是否存在前后缀相同的情况，且取最长的，发现 ab 是最长的公共前后缀。这意味着，在 x 和 c 发生不匹配时，x 左边的子串一定是 ab。因此也意味着，因为 x 左边的子串ab和子串（abcdab）后缀是一定相同的，子串（abcdab）后缀和其前缀也一定是相同的，故不需要再次去匹配前缀（ab）；下一次匹配可以从 x 和 c（pattern[2]） 开始。

也就是说，我们不需要在主串中向前回顾，去寻找下一个匹配点在哪里，现在我们从 x 和 c 这里开始，那是因为这个子串（abcdab）的后缀（ab）也是前缀（ab），而后缀（ab）已经和x 左边的子串ab匹配过了，那么没有理由再去匹配一遍前缀（ab）了，因此我们从x 和 c开始匹配 

此时 x 和 c 匹配失败，我们检查 c 前面的子串（ab）是否存在前后缀相同的情况，发现没有！因此意味着我们下一个比较对象将从 x 和 a 开始

此时发现还是匹配失败，而 j = 0,退无可退了，那么就 i++；（指向下一个位置）

匹配成功的话就 i++; j++;

当 i 指向 d ，j 指向 y 的时候，发生匹配失败！我们检查 y 前面的子串（abcdabc）是否存在前后缀相同的情况，且取最长的，发现 abc 是最长的公共前后缀。这意味着，在 d 和 y 发生不匹配时，y 之前的已经匹配了，y之前的子串（abcdabc）的后缀（abc）和文本串中 d 的前面子串（abc）相同。而子串（abcdabc）的后缀（abc）和前缀（abc）相同，可以说后缀也是前缀，那么就没有理由再一次去匹配abc。下一次比较可以从模式串的d开始，也就是从当前文本串的 d 和 模式串的 d 开始匹配 

匹配成功的话就 i++; j++;

此时 i 越界，j 越界（匹配成功），结束！

二、D数组

此时 pattern[i] != pattern[j]，即 b != a,匹配失败，此时 j = 0,继续 i++

---

此时 pattern[i] != pattern[j]，即 c != a,匹配失败，此时 j = 0,继续 i++

---

此时 pattern[i] != pattern[j]，即 d != a,匹配失败，此时 j = 0,继续 i++

---

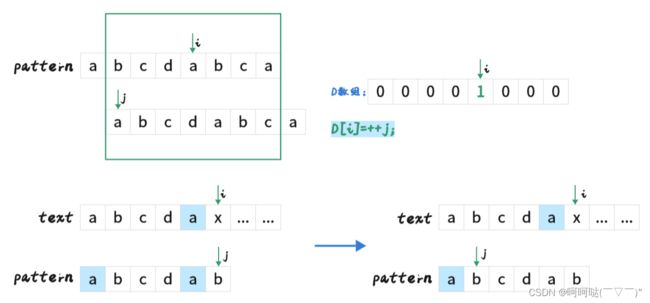
此时 pattern[i] == pattern[j]，即 a == a,匹配成功，此时记录D[i] = ++j;即 j = 1，D[4] = 1; 然后继续i++;（注意 j++ 操作已经在 D[i] = ++j 中了）

---

此时 pattern[i] == pattern[j]，即 b == b,匹配成功，此时记录D[i] = ++j;即 j = 2，D[5] = 2; 然后继续i++;（注意 j++ 操作已经在 D[i] = ++j 中了）

---

此时 pattern[i] == pattern[j]，即 c == c,匹配成功，此时记录D[i] = ++j;即 j = 3，D[6] = 3; 然后继续i++;（注意 j++ 操作已经在 D[i] = ++j 中了）

---

此时 pattern[i] != pattern[j]，即 a != d,匹配失败，此时 j = 3,执行 j = D[j-1]; 即 j = D[3-1] = D[2] = 0;

那么 j = 0；继续判断 j 和 i 所指向的字符是否匹配

---

此时 pattern[i] == pattern[j]，即 a == a,匹配成功，此时记录D[i] = ++j;即 j = 1，D[7] = 1; 然后继续i++;（注意 j++ 操作已经在 D[i] = ++j 中了）

---

此时 i 越界，终止！

---

探究一下，这其中的一个值的意义，以此类推：

这意味着在子串abcda有最大公共前后缀为a，其前后缀相同都为a,因此我们匹配了 后缀a 和 文本串 x 前面的子串a,也就意味着 前缀a 和文本串 x 前面的子串a已经匹配了，所以下一个我们检查的是 x 和 b

C++代码：

#include
#include
using namespace std;

void print_matching_result(string s, int start) {
    for (int i = 0; i < start; i++)
        cout << " ";
    cout< 0) j = D[j - 1];
            else i++;
        }
    }
}

void kmp(string text, string pattern) {
    cout << "**********************************************" << endl;
    cout << text << endl;
    int i = 0, j = 0, nt = text.size(), np = pattern.size();
    int* D = new int[np]();
    getD(D, pattern);
    while (i < nt) {
        if (pattern[j] == text[i]) {
            i++, j++;
            if (j == np) {
                print_matching_result(pattern, i - j);
                j = D[np - 1];
            }
        }
        else {
            if (j > 0) j = D[j - 1];
            else i++;
        }
    }
}

int main()
{
    kmp("ABABABABC", "ABAB");
    kmp("ABABCABAB", "ABAB");
    kmp("AAAAAAA", "AAA");
    kmp("ABABABC", "ABABC");
    kmp("XYXZdeOXZZKWXYZ", "WXYZ");
    kmp("GCAATGCCTATGTGACCTATGTG", "TATGTG");
    kmp("AGATACGATATATAC", "ATATA");
    kmp("CATCGCGGAGAGTATAGCAGAGAG", "GCAGAGAG");
    return 0;
}

我的往期文章（详解KMP算法核心原理：j = D[j-1]）：

KMP 算法 + 详细笔记 + 核心分析 j = D[j-1]-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/133848188?spm=1001.2014.3001.5501参考和推荐B站视频：

【中文字幕】Knuth–Morris–Pratt(KMP)_Pattern_Matching(Substring_search)_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV18k4y1m7Ar?p=1&vd_source=a934d7fc6f47698a29dac90a922ba5a3

实战力扣题，感兴趣的话可以看一下我的往期文章：

leetCode 214.最短回文串 + KMP-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/133915196?spm=1001.2014.3001.5501