唐宇迪机器学习实战课程笔记(全)

机器学习模型的参数，不是直接数学求解，而是利用数据，进行迭代epoch，梯度下降优化求解。

1. 线性回归

1.1线性回归理论

• 目标：更好的拟合连续函数(分割连续样本空间的平面h(·))
  

• ${\epsilon }^{(i)}$是 真实值$y^{(i)}$ 与 预测值$h_{\theta }(x)={\theta }^T{x}^{(i)}$之间的误差
  

• 求解参数$\theta$ ：误差项$\epsilon$服从高斯分布，利用最大似然估计，转换为最小二乘法
  

• 从最小二乘法得到目标函数$J(\theta )$，为求其最值，利用梯度下降算法，沿偏导数(梯度)反方向，迭代更新计算，求解参数$\theta$ 。
  

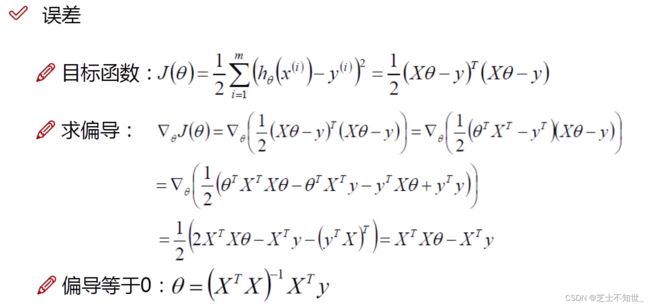
• 梯度下降算法：BatchGD批量梯度下降、SGD随机梯度下降、Mini-BatchGD小批量梯度下降(实用)
  batch一般设为$2^5$=64、$2^6$=128、$2^7$=256，越大越好
  
  GD的矩阵运算：
  

• 学习率lr：开始设1e-3，逐渐调小到1e-5
  

1.2线性回归实战

数据预处理中normalize标准化作用：对输入全部数据$\frac{X-\mu }{\sigma }$，使得不同值域的输入$x_i$、$x_j$分布在同一取值范围。如$x_i\in [0.1,0.5]$，$x_j\in [10,50]$，normalize使其同一值域。

prepare__for_train.py

"""Prepares the dataset for training"""

import numpy as np
from .normalize import normalize
from .generate_sinusoids import generate_sinusoids
from .generate_polynomials import generate_polynomials


def prepare_for_training(data, polynomial_degree=0, sinusoid_degree=0, normalize_data=True):

    # 计算样本总数
    num_examples = data.shape[0]

    data_processed = np.copy(data)

    # 预处理
    features_mean = 0
    features_deviation = 0
    data_normalized = data_processed
    if normalize_data:
        (
            data_normalized,
            features_mean,
            features_deviation
        ) = normalize(data_processed)

        data_processed = data_normalized

    # 特征变换sinusoidal
    if sinusoid_degree > 0:
        sinusoids = generate_sinusoids(data_normalized, sinusoid_degree)
        data_processed = np.concatenate((data_processed, sinusoids), axis=1)

    # 特征变换polynomial
    if polynomial_degree > 0:
        polynomials = generate_polynomials(data_normalized, polynomial_degree, normalize_data)
        data_processed = np.concatenate((data_processed, polynomials), axis=1)

    # 加一列1
    data_processed = np.hstack((np.ones((num_examples, 1)), data_processed))

    return data_processed, features_mean, features_deviation

linearRegressionClass.py

class LinearRegression_:

    def __init__(self, data, labels, polynomial_degree=0, sinusoid_degree=0, normalize_data=True):
        """
        1.对数据进行预处理操作
        2.先得到所有的特征个数
        3.初始化参数矩阵
        """
        (data_processed,
         features_mean,
         features_deviation) = prepare_for_training(data, polynomial_degree, sinusoid_degree, normalize_data=True)

        self.data = data_processed
        self.labels = labels
        self.features_mean = features_mean
        self.features_deviation = features_deviation
        self.polynomial_degree = polynomial_degree
        self.sinusoid_degree = sinusoid_degree
        self.normalize_data = normalize_data

        num_features = self.data.shape[1]
        self.theta = np.zeros((num_features, 1))

    def train(self, alpha=0.01, num_iterations=500):
        """
                    训练模块，执行梯度下降
        """
        cost_history = self.gradient_descent(alpha, num_iterations)
        return self.theta, cost_history

    def gradient_descent(self, alpha, num_iterations):
        """
                    实际迭代模块，会迭代num_iterations次
        """
        cost_history = []
        for _ in range(num_iterations):
            self.gradient_step(alpha)
            cost_history.append(self.cost_function(self.data, self.labels))
        return cost_history

    def gradient_step(self, alpha):
        """
                    梯度下降参数更新计算方法，注意是矩阵运算
        """
        num_examples = self.data.shape[0]
        prediction = LinearRegression_.hypothesis(self.data, self.theta)
        delta = prediction - self.labels
        theta = self.theta
        theta = theta - alpha * (1 / num_examples) * (np.dot(delta.T, self.data)).T
        self.theta = theta

    def cost_function(self, data, labels):
        """
                    损失计算方法
        """
        num_examples = data.shape[0]
        delta = LinearRegression_.hypothesis(self.data, self.theta) - labels
        cost = (1 / 2) * np.dot(delta.T, delta) / num_examples
        return cost[0][0]

    @staticmethod
    def hypothesis(data, theta):
        predictions = np.dot(data, theta)
        return predictions

    def get_cost(self, data, labels):
        data_processed = prepare_for_training(data,
                                              self.polynomial_degree,
                                              self.sinusoid_degree,
                                              self.normalize_data
                                              )[0]

        return self.cost_function(data_processed, labels)

    def predict(self, data):
        """
                    用训练的参数模型，与预测得到回归值结果
        """
        data_processed = prepare_for_training(data,
                                              self.polynomial_degree,
                                              self.sinusoid_degree,
                                              self.normalize_data
                                              )[0]

        predictions = LinearRegression_.hypothesis(data_processed, self.theta)

        return predictions

单输入变量线性回归：
$$y={\theta }^1{x}^1+b$$
single_variate_LinerRegression.py

import os
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from linearRegressionClass import *

dirname = os.path.dirname(__file__)
data = pd.read_csv(dirname + "/data/world-happiness-report-2017.csv", sep=',')
train_data = data.sample(frac=0.8)
test_data = data.drop(train_data.index)

# 选定考虑的特征
input_param_name = 'Economy..GDP.per.Capita.'
output_params_name = 'Happiness.Score'

x_train = train_data[[input_param_name]].values
y_train = train_data[[output_params_name]].values
x_test = test_data[[input_param_name]].values
y_test = test_data[[output_params_name]].values

# 用创建的随机样本测试
# 构造样本的函数
# def fun(x, slope, noise=1):
#     x = x.flatten()
#     y = slope*x + noise * np.random.randn(len(x))
#     return y

#     # 构造数据
# slope=2
# x_max = 10
# noise = 0.1
# x_train = np.arange(0,x_max,0.2).reshape((-1,1))
# y_train = fun(x_train, slope=slope, noise=noise)
# x_test = np.arange(x_max/2, x_max*3/2, 0.2).reshape((-1,1))
# y_test = fun(x_test, slope=slope, noise=noise)

#     #观察训练样本和测试样本
# # plt.scatter(x_train, y_train, label='train data', c='b')
# # plt.scatter(x_test, y_test, label='test data', c='k')
# # plt.legend()
# # plt.title('happiness - GDP')
# # plt.show()


#     #测试 - 与唐宇迪的对比
# lr = LinearRegression()
# lr.fit(x_train, y_train)
# print(lr.predict(x_test))
# print(y_test)

# y_train = y_train.reshape((-1,1))
# lr = LinearRegression_(x_train, y_train)
# lr.train()
# print(lr.predict(x_test))
# print(y_test)

lr = LinearRegression()
lr.fit(x_train, y_train, alpha=0.01, num_iters=500)
y_pre = lr.predict(x_test)
print("开始损失和结束损失", lr.cost_hist[0], lr.cost_hist[-1])
# iters-cost curve
# plt.plot(range(len(lr.cost_hist)), lr.cost_hist)
# plt.xlabel('Iter')
# plt.ylabel('cost')
# plt.title('GD')
# plt.show()
plt.scatter(x_train, y_train, label='Train data')
plt.scatter(x_test, y_test, label='test data')
plt.plot(x_test, y_pre, 'r', label='Prediction')
plt.xlabel(input_param_name)
plt.ylabel(output_params_name)
plt.title('Happy')
plt.legend()
plt.show()

多输入变量线性回归
$$y=\sum _{i=1}^n{\theta }^i{x}^i+b$$
非线性回归
1.对原始数据做非线性变换，如$x->ln(x)$
2.设置回归函数的复杂度最高$x^n$

2.训练调参基本功(线性回归、岭回归、Lasso回归)

构建线性回归方程拟合数据点

2.1 线性回归模型实现

准备数据，预处理perprocess（标准化normalize），划分数据集（训练集train和测试集test），导包（sklearn或自己写的class），实例化LinearRegression，设置超参数（lr/eopch/batch…），是否制定learning策略（学习率衰减策略），权重参数初始化init_weight（随机初始化/迁移学习），训练（fit或自己写for迭代计算梯度更新参数），预测

2.2不同GD策略对比

MiniBatch梯度下降实例

theta_mini_list = []
cost_mini_list = []

batch_size = 10
n_epochs = 50
iters_per_epoch = int(num_samples / batch_size) + 1

theta = np.random.randn(num_features, 1)

# 学习率衰减策略
def learn_schedule(t):
    t0 = 10
    t1 = 2500
    return t0/(t1+t)

def cost(X_b, y, theta):
    num_features = X_b.shape[1]
    num_samples = X_b.shape[0]
    delta = y - np.dot(X_b,theta)
    return 1/(2*num_samples) * np.sum(delta ** 2)

theta_mini_list.append(theta.copy())
loss_mini = cost(X_b, y, theta)
cost_mini_list.append(loss_mini)

epoch = 0
for i in range(1000000):
    batch_mask = np.random.permutation(num_samples)[:10]
    X_batch = X_b[batch_mask]
    y_batch = y[batch_mask]

    grads = - 1/(batch_size) * np.dot(X_batch.T, (y_batch - X_batch.dot(theta)))
    alpha = learn_schedule(i)
    theta -= alpha * grads
    
    if not i%iters_per_epoch:
        loss_mini = cost(X_b, y, theta)
        cost_mini_list.append(loss_mini)
        theta_mini_list.append(theta.copy())
    
    epoch += 1
    if epoch >= n_epochs:
        break

theta_mini_list = np.array(theta_SGD_list)
theta_mini_list[-3:]

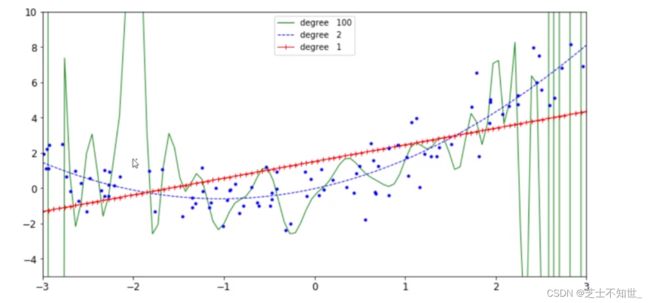
2.3多项式曲线回归

最高次项>1

sklearn.preporcessing.PloynomialFeatures(degree=最高项次幂,include_bias=是否包含偏置项)

不同degree拟合的效果

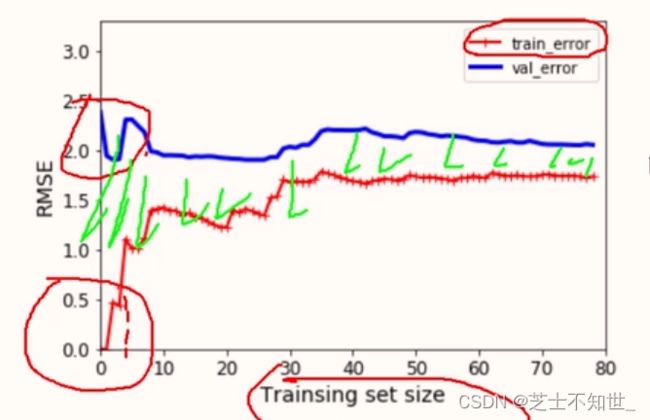
2.4过拟合和欠拟合

训练集数据量与过拟合风险：
数据越多，train和test的error差异越小，过拟合风险越低。(形象比喻：学生做题(train)和考试(test)的关系，学生做练习题(train_size)越多，考试(test)发挥越好，过拟合就是平时做题少，导致考试不如平时。)

多项式回归的高次项次数与过拟合风险：
degree次数越高，过拟合风险越大。

import scipy.io
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
def plot_learning_curves(model, X, y):
    # 切分train和val
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
    train_errors ,test_errors = [], []
    # 每次训练m个样本(对比不同样本数量下的训练效果)
    for m in range(1,len(X_train)):
        # 本次训练只需要前m个数据
        model.fit(X_train[:m],y_train[:m])
        # 计算训练集和测试集预测结果，用于计算训练集和测试集上的误差
        y_train_pre = model.predict(X_train[:m])
        y_test_pre = model.predict(X_test)  # 测试集要用全部数据
        train_errors.append(mean_squared_error(y_train[:m], y_train_pre))
        test_errors.append(mean_squared_error(y_test, y_test_pre))
    # RMSE=MSE开方
    plt.plot(np.sqrt(train_errors),'r-+',linewith=2,label="train")
    plt.plot(np.sqrt(test_errors),'b-+',linewith=2,label="test")
    plt.legend()

model = LinearRegression()
X, y = [], []
plot_learning_curves(model, X, y)
plt.xlabel('Training Size')
plt.ylabel('RMSE error')
plt.axis([0,80,0,3.3])
plt.show()

2.5正则化

正则化：在loss添加正则项(惩罚偏好，包括L1和L2)，缓解过拟合。

L1正则项： L1正则化最大的特点是能稀疏矩阵，进行庞大特征数量下的特征选择。L1是模型各个参数的绝对值之和
L2正则项：(推荐) L2正则能够有效的防止模型过拟合，解决非满秩下求逆困难的问题。L2是模型各个参数的平方和的开方值。

正则项的系数$\alpha$：$\alpha$称为正则化参数，如果$\alpha$选取过大，会把所有参数w均最小化，造成欠拟合；如果$\alpha$选取过小，会导致对过拟合问题解决不当，因此$\alpha$的选取是一个技术活。

为了缓解线性回归过拟合，使用正则化改进：1.岭回归 2.Lasso回归
岭回归正则化loss：线性回归的MSEloss + L2正则项(平方和根)，(效果：使权重可能小，且不同权重值差异更小) 其中$\alpha$是正则项惩罚力度：$$loss=\sqrt[]{||y-Xw|{|}^2}+\alpha \ast \sqrt[]{||w|{|}^2}$$

岭回归是加了L2正则项的最小二乘，主要适用于过拟合严重或各变量之间存在多重共线性的时候，岭回归是有bias的，这里的bias是为了让variance更小。

左图表示一次线性岭回归，右图表示高次非线性岭回归。
根据右图可知，$\alpha$越大，曲线的斜率浮动变化越大(即不同权重w差异越大)

Lasso回归正则化loss：线性回归的MSEloss + L1正则项(绝对值和)，LASSO 回归同样是通过添加正则项来改进普通最小二乘法，不过这里添加的是 L1 正则项。即：
$$loss=\sqrt[]{||y-Xw|{|}^2}+\alpha \ast ||w||$$

3.分类模型评估(Mnist实战SGD_Classifier)

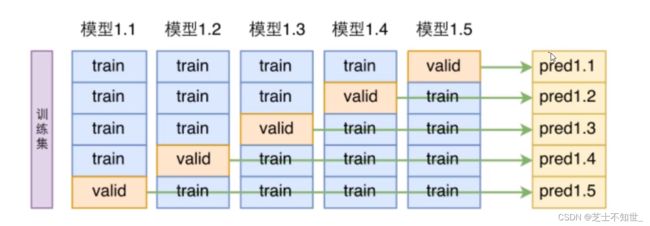
3.1 K折交叉验证K-fold cross validation

①切分完训练集training和测试集testing后
②再对training进行均分为K份
③训练的迭代将进行K轮，每轮将其中K-1份作为training，1份作为验证机validation，边训练train边验证valid
④最后训练和验证的epoch结束了，再用测试集testing进行测试。
常用的K=5/10

import numpy as np
import os
import matplotlib
import matplotlib.pyplot as plt

plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
import warnings

warnings.filterwarnings('ignore')
np.random.seed(42)

# from sklearn.datasets import fetch_openml
# mnist = fetch_openml('MNIST original')
# 也可以GitHub下载，手动加载
import scipy.io

mnist = scipy.io.loadmat('MNIST-original')
# 图像数据 (28x28x1)的灰度图，每张图像有784个像素点(=28x28x1)
# print(mnist)  # 字典key=data和label，数据存在对应的value中
X, y = mnist['data'], mnist['label']
# print(X.shape)  # data  784 x 70000,每列相当于一张图，共70000张图像
# print(y.shape)  # label 1 x 70000，共70000个标签


# 划分数据，训练集training，测试集testing，train取前60000，test取后10000
# 列切片
X_train, X_test, y_train, y_test = X[:, :60000], X[..., 60000:], y[:, :60000], y[..., 60000:]
# 训练集数据洗牌打乱
import numpy as np

X_train = np.random.permutation(X_train)
y_train = np.random.permutation(y_train)

# 因为后面要画混淆矩阵，最好是2分类任务：0-10的数字判断是不是5
# 将label变为true和false
y_train_5 = (y_train == 5)[0]
y_test_5 = (y_test == 5)[0]

# print(X_train.shape)
# print(y_train_5.shape)

X_train = X_train.T
X_test = X_test.T
# 创建线性模型SGDClassifier
from sklearn.linear_model import SGDClassifier

sgd_clf = SGDClassifier(max_iter=50, random_state=42)
# sgd_clf.fit(X_train, y_train_5)  # 训练
# print(sgd_clf.predict(X_test))

# K折交叉验证 划分训练集training，验证集validation，并训练

# 方法一：
from sklearn.model_selection import cross_val_score
kfold=5
acc=cross_val_score(sgd_clf, X_train, y_train_5, cv=kfold, scoring='accuracy')  ## cv是折数
avg_acc = sum(acc) / kfold
print("avg_acc=", avg_acc)
# 返回每折的acc：[0.87558333 0.95766667 0.86525 0.91483333 0.94425]


# 方法二
from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone  # K折中每折训练时，模型带有相同参数
kfold = 5
acc = []
skfold = StratifiedKFold(n_splits=kfold, random_state=42)
i = 1
for train_idx, test_idx in skfold.split(X_train, y_train_5):
    # 克隆模型
    clone_clf = clone(sgd_clf)

    # 划分训练集training和验证集validation
    X_train_folds = X_train[train_idx]
    X_val_folds = X_train[test_idx]
    y_train_folds = y_train_5[train_idx]
    y_val_folds = y_train_5[test_idx]
    # 模型训练
    clone_clf.fit(X_train_folds, y_train_folds)
    # 对每折进行预测，计算acc
    y_pred = clone_clf.predict(X_val_folds)
    n_correct = sum(y_pred == y_val_folds)
    acc.append(n_correct / len(y_pred))
    print("Split", i, "/", kfold, "Done.")
    i = i + 1
# 平均acc
avg_acc = sum(acc) / kfold
print("avg_acc=", avg_acc)

3.2 混淆矩阵Confusion Matrix

分类任务，下例对100人进行男女二分类，100中，模型检测有50人为男(实际全为男)，50人为女(实际20为女 30为男)。

一个完美的分类是只有主对角线非0，其他都是0
n分类：混淆矩阵就是nxn

接上个代码

from sklearn.model_selection import cross_val_predict
# 60000个数据，进行5折交叉验证
# cross_val_predict返回每折预测的结果的concat，每折12000个结果，5折共60000个结果
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=kfold)
# 画混淆矩阵
from sklearn.metrics import confusion_matrix
confusion=confusion_matrix(y_train_5, y_train_pred)  # 传入train的标签和预测值
# 2分类的矩阵就是2x2的[[TN,FP],[FN,TP]]

plt.figure(figsize=(2, 2))  # 设置图片大小
# 1.热度图，后面是指定的颜色块，cmap可设置其他的不同颜色
plt.imshow(confusion, cmap=plt.cm.Blues)
plt.colorbar()  # 右边的colorbar
# 2.设置坐标轴显示列表
indices = range(len(confusion))
classes = ['5', 'not 5']
# 第一个是迭代对象，表示坐标的显示顺序，第二个参数是坐标轴显示列表
plt.xticks(indices, classes, rotation=45)  # 设置横坐标方向，rotation=45为45度倾斜
plt.yticks(indices, classes)
# 3.设置全局字体
# 在本例中，坐标轴刻度和图例均用新罗马字体['TimesNewRoman']来表示
# ['SimSun']宋体；['SimHei']黑体，有很多自己都可以设置
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 4.设置坐标轴标题、字体
# plt.ylabel('True label')
# plt.xlabel('Predicted label')
# plt.title('Confusion matrix')
plt.xlabel('预测值')
plt.ylabel('真实值')
plt.title('混淆矩阵', fontsize=12, fontfamily="SimHei")  # 可设置标题大小、字体
# 5.显示数据
normalize = False
fmt = '.2f' if normalize else 'd'
thresh = confusion.max() / 2.
for i in range(len(confusion)):  # 第几行
    for j in range(len(confusion[i])):  # 第几列
        plt.text(j, i, format(confusion[i][j], fmt),
                 fontsize=16,  # 矩阵字体大小
                 horizontalalignment="center",  # 水平居中。
                 verticalalignment="center",  # 垂直居中。
                 color="white" if confusion[i, j] > thresh else "black")
save_flg = True
# 6.保存图片
if save_flg:
    plt.savefig("confusion_matrix.png")
# 7.显示
plt.show()

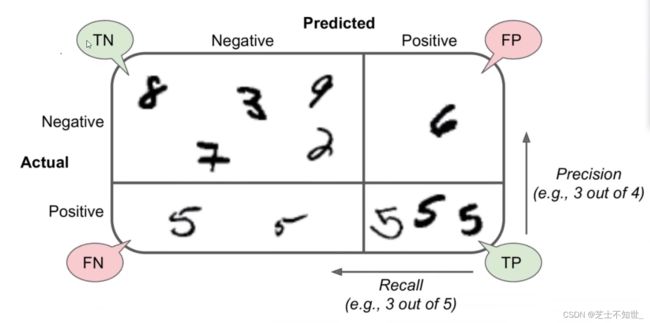
3.3 准确率accuracy、精度precision、召回率recall、F1

sklearn.metrics中有对应的计算函数(y_train, y_train_pred)

准确率accurcy=预测正确个数/总样本数=$\frac{TP+TN}{TP+TN+FP+FN}$

精度precision=$\frac{TP}{TP+FP}$

召回率recall=$\frac{TP}{TP+FN}$

F1 Score=$\frac{2\ast TP}{2\ast TP+FP+FN}$=$\frac{2\ast precision\ast recall}{precision+recall}$

接上面代码

from sklearn.metrics import accuracy_score,precision_score,recall_score,f1_score
accuracy=accuracy_score(y_train_5,y_train_pred)
precision=precision_score(y_train_5,y_train_pred)
recall=recall_score(y_train_5,y_train_pred)
f1_score=f1_score(y_train_5,y_train_pred)
print("accuracy=",accuracy)
print("precision=",precision)
print("recall=",recall)
print("f1_score",f1_score)

3.4 置信度confidence

confidence：模型对分类预测结果正确的自信程度

y_scores=cross_val_predict(sgd_clf,X_train,y_train_5,kfold,method=‘decision_function’)方法返回每个输入数据的confidence，我们可以手动设置阈值t，对预测结果进行筛选，只有confidence_score>t，才视为预测正确。

precision, recall, threshholds = precision_recall_curve(y_train_5,y_scores)函数可以自动设置多个阈值，且每个阈值都对应计算一遍precision 和 recall

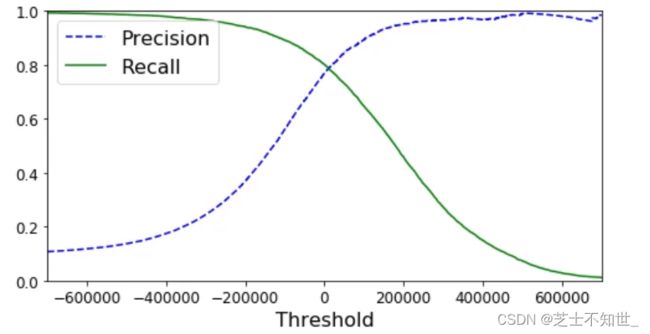
接上面代码

# 自动生成多个阈值，并计算precision, recall
y_scores = cross_val_predict(sgd_clf,X_train,y_train_5,kfold,method='decision_function')
from sklearn.metrics import precision_recall_curve
precision, recall, threshholds = precision_recall_curve(y_train_5,y_scores)

3.5 ROC曲线

分类任务可以画出ROC曲线：理想的分类器是逼近左上直角，即曲线下方ROC AUC面积接近1.

接上面代码

# 分类任务，画ROC曲线
from sklearn.metrics import roc_curve
fpr,tpr,threshholds=roc_curve(y_train_5,y_scores)
def plot_roc_curve(fpr,tpr,label=None):
    plt.plot(fpr,tpr,linewidth=2,label=label)
    plt.plot([0,1],[0,1],'k--')
    plt.axis([0,1,0,1])
    plt.xlabel('False Positive Rate', fontsize=16)
    plt.ylabel('True Positive Rate', fontsize=16)
plt.figure(figsize=(8,6))
plot_roc_curve(fpr,tpr)
plt.show()

# 计算roc_auc面积
from sklearn.metrics import roc_auc_score
roc_auc_score=roc_auc_score(y_train_5,y_train_pred)

4. 逻辑回归Logistic Regression

4.1 逻辑回归原理

最简单的分类算法，因为要对样本空间进行分类，所以决策边界是非线性的，Sigmod函数实现2分类，Sotmax实习多分类。

非线性：使用Sigmoid函数，将线性回归值->二分类非线性的逻辑概率，引入非线性信息。

逻辑回归预测函数 = sigmod/Softmax(线性回归函数) -> 二/多分类整合

二分类：$P(y|x;\theta )=h_{\theta }(x{)}^y\ast (1-h_{\theta }(x{)}^{1-y})$

利用最大似然，计算loss函数

loss梯度下降，求梯度

迭代更新参数

4.2 多分类逻辑回归实现

将多分类任务拆解成多个2分类任务，如ABC三类，分别3次划分AB、BC、AC之间的分类边界。

5. SVM支持向量机

支持向量机（SVM）是一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面，可以将问题化为一个求解凸二次规划的问题。与逻辑回归和神经网络相比，支持向量机，在学习复杂的非线性方程时提供了一种更为清晰，更加强大的方式。

支持向量机算法分类和回归方法的中都支持线性/线性可分和非线性/线性不可分类型的数据类型。还可以分为硬间距和软间距。

• 在线性-线性可分时，在原空间寻找两类样本的最优分类超平面。
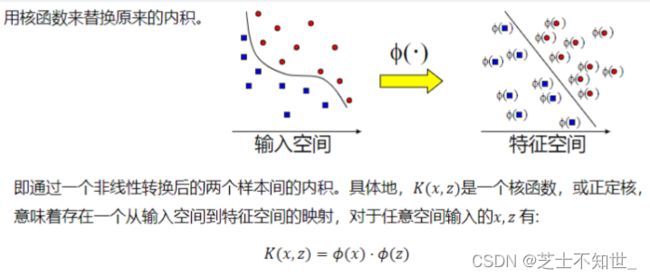
• 在非线性-线性不可分时，通过核函数使用非线性映射将低维度输入空间的样本映射到高维度空间使其变为线性可分，这样就可以在该特征空间中寻找最优分类超平面。低维平面不可分，为了使数据可分，需要通过一个函数将原始数据映射到高维空间，从而使得数据在高维空间很容易可分，需要通过一个函数将原始数据映射到高维空间，从而使得数据在高维空间很容易区分，这样就达到数据分类或回归的目的，而实现这一目标的函数称为核函数。
• 硬间隔，指的就是完全分类准确，不能存在分类错误的情况。
• 软间隔，就是允许一定量的样本分类错误。
  

SVM使用准则： n为特征数，m 为训练样本数。

• 如果相较于m而言，n要大许多，即训练集数据量不够支持我们训练一个复杂的非线性模型，我们选- 用逻辑回归模型或者不带核函数的支持向量机。
• 如果n较小，而且m大小中等，例如n在 1-1000 之间，而m在10-10000之间，使用高斯核函数的支持向量机。
• 如果n较小，而m较大，例如n在1-1000之间，而m大于50000，则使用支持向量机会非常慢，解决方案是创造、增加更多的特征，然后使用逻辑回归或不带核函数的支持向量机。

优点：

• 支持向量机算法可以解决小样本情况下的机器学习问题，简化了通常的分类和回归等问题。
• 由于采用核函数方法克服了维数灾难和非线性可分的问题，所以向高维空间映射时没有增加计算的复杂性。换句话说，由于支持向量计算法的最终决策函数只由少数的支持向量所确定，所以计算的复杂性取决于支持向量的数目，而不是样本空间的维数。
• 支持向量机算法利用松弛变量可以允许一些点到分类平面的距离不满足原先要求，从而避免这些点对模型学习的影响。

缺点：

• 支持向量机算法对大规模训练样本难以实施。这是因为支持向量机算法借助二次规划求解支持向量，这其中会涉及m阶矩阵的计算，所以矩阵阶数很大时将耗费大量的机器内存和运算时间。
  经典的支持向量机算法只给出了二分类的算法，而在数据挖掘的实际应用中，一般要解决多分类问题，但支持向量机对于多分类问题解决效果并不理想。
• SVM算法效果与核函数的选择关系很大，往往需要尝试多种核函数，即使选择了效果比较好的高斯核函数，也要调参选择恰当的参数。另一方面就是现在常用的SVM理论都是使用固定惩罚系数C，但正负样本的两种错误造成的损失是不一样的。

MLP与SVM分类的区别：
感知机的目的是尽可能使得所有样本分类正确，而SVM的目标是分类间隔最大化。支持向量机追求大致正确分类的同时，一定程度上避免过拟合。感知机使用的学习策略是梯度下降，而SVM采用的是由约束条件构造拉格朗日函数，然后求偏导为0求得极值点。

5.1 SVM理论推导

线性硬间距：



线性软间距：



非线性
常见核函数：

详细的：
求一个分类的超平面，距最近的点的距离越大越好。

计算 平面外一点x 到 超平面 的距离：
平面上两个点$x^{{}^{\prime }}$和$x^{{}^{\prime \prime }}$满足平面方程$w^{T}x+b=0$，其中w是法向量。

2分类SVM，决策边界(超平面)，决策方程(线性：$y(x)=w^{T}x+b$，非线性：对x用核函数$\phi (x)$变换$y(x)=w^T\phi (x)+b$ )

SVM优化的目标：min(样本到超平面的距离)（用上述方法去掉绝对值）
|$w^T\phi (x_i)+b$| -> $y_i\cdot y(\phi (x_i))$ -> $y_i\cdot (w^T\phi (x_i)+b)$

目标函数：①先求不同样本点$x_i$中距离最近的样本点，②再求该样本点与超平面(w,b)距离的最大值。③放缩变换($y_i\cdot (w^T\phi (x_i)+b)$>=1)，分母->1，化简目标函数=${\max }_{w,b}\frac{1}{||w||}$。④将求max->min，目标函数=${\max }_{w,b}\frac{w^2}{2}$

即带约束的优化问题，条件：$y_i\cdot (w^T\phi (x_i)+b)>=1$之下，求目标函数：${\max }_{w,b}\frac{w^2}{2}$

拉格朗日乘子法：专门解决带约束优化问题，将条件代入目标函数中。
引入变量$\alpha (对每个x_i都有{\alpha }_i)$，只需根据$\alpha$进行优化，求得$\alpha$后再求为w和b。

对偶原则，min和max先后不影响。
SVM求解：变成两步极值求解(求偏导、max变min)。



软间隔：引入松弛变量



非线性(线性不可分)：

核函数：只用高斯核函数(原始特征->高斯距离特征)就可以了。

5.2 非线性软间隔SVM实战