雷达有源干扰识别仿真

各类干扰信号

  基于数字射频存储(DRFM)技术的雷达干扰系统有三种工作方式：转发方式、应答方式和噪声方式，即，对应有三种干扰类型。

噪声干扰

  DRFM干扰系统在噪声工作方式下不但可以产生传统噪声干扰，还可以通过将数字噪声调制到干扰机接收到的$s(t)$上而产生灵巧噪声干扰。

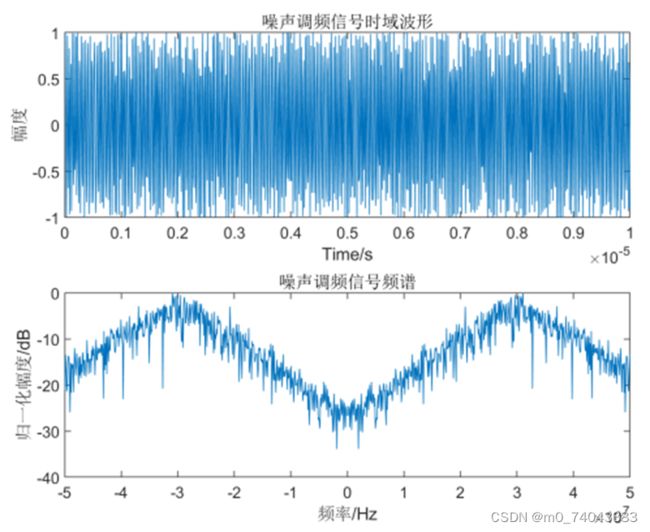
噪声调频信号

   利用噪声信号对射频信号的频率进行调制，即，让射频信号的频率按照调制噪声的规律进行变化，其数学模型可表示为：
$$J(t)=U_{0}cos[w_{0}t+2\pi K_{FM}{\int }_0^{t}u(t^{{}^{\prime }})d{t}^{{}^{\prime }}+\phi ]$$
   噪声调频干扰是一个广义平稳随机过程，$u(t)$为调制噪声，它是均值为零的广义平稳随机过程， $\phi$ 为相位函数，服从$[0,2\pi ]$的均匀分布，并且与调制噪声$u(t)$相互独立，载频$w_0$为常数，$K_{FM}$为调频斜率。

噪声调幅信号

   调幅是指载波信号的幅度随调制信号电压的变化规律进行变化，而载波频率保持不变，噪声调幅干扰是用噪声对射频信号的幅度进行调制而产生的，其数学模型可表示为：
$$J(t)=(U_0+U_n(t))cos(w_{0}t+\phi )$$
   其中，$U_0$为载波电压，调制噪声$U_n(t)$是均值为0，方差为${\sigma }_n^2$的高斯带限白噪声，$\phi$为相位函数，服从$[0,2\pi ]$的均匀分布，并且与$U_n(t)$相互独立，载频$w_0$为常数，噪声的有效调制系数为$m_{Ae}={\sigma }_n/U_0$。

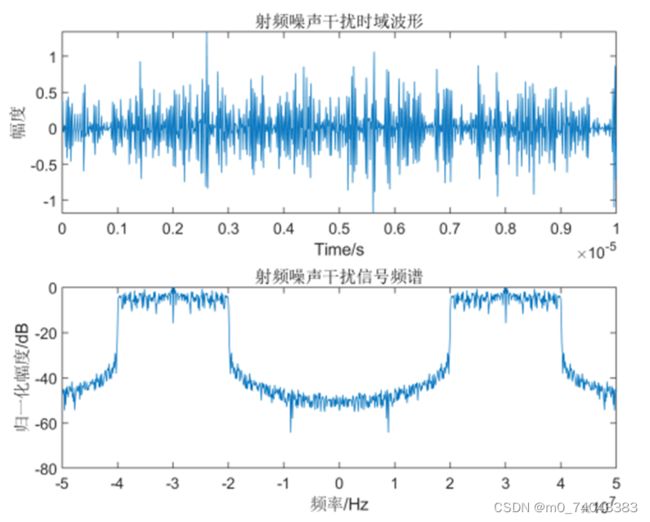
射频噪声干扰

   通过对白噪声进行滤波及高频放大产生，因此，又被称为纯噪声干扰，其数学模型可表示为：
$$J(t)=U_n(t)cos[w_{0}t+\phi (t)]$$
  其中，$U(t)$服从瑞利分布，$\phi (t)$为相位函数，服从$[0,2\pi ]$的均匀分布，并且与$U_n(t)$相互独立，载频 $w_0$ 为常数，它远大于$J(t)$谱宽，所以射频噪声干扰是一个窄带高斯随机过程。

噪声卷积干扰

   噪声卷积干扰（CN，卷积调制灵巧噪声）是一种基于DRFM技术的卷积调制干扰，旨在利用目标信号产生想干干扰。雷达发射的信号被干扰机接收再放大滤波后，下变频变为中频信号然后存储到数字射频存储器（DRFM），经过一定处理后再上变频雷达信号所在频段。另一路，雷达信号经过接收和处理后，控制噪声单元产生合理长度和类型的噪声数据。两路输出信号在卷积器例完成卷积运算，最后可以产生一种效果较好的灵巧噪声干扰波形。设输入DRFM的雷达信号为$s(t)$。窄带高斯噪声信号为$n(t)$。$s(t-\tau )$与 $n(t)$ 卷积，进行噪声卷积调制得到输出卷积调制灵巧噪声干扰信号，其数学表达式为：
$$J(t)=s(t-\tau )⨂n(t)$$

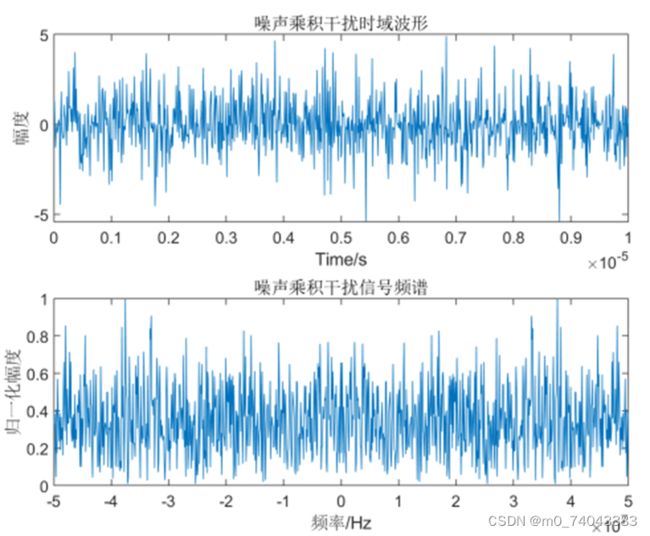
噪声乘积干扰

噪声乘积干扰（NP，乘积调制灵巧噪声）产生原理域卷积调制灵巧噪声类似，设输入DRFM的雷达信号为$s(t)$，窄带高斯噪声信号为$n(t)$。$s(t-\tau )$ 与 $n(t)$ 相乘，进行噪声乘积调制得到输出乘积调制灵巧噪声干扰信号，其数学表达式为：
$$J(t)=s(t-\tau )\times n(t)$$

拖引欺骗干扰

   DRFM干扰系统工作在转发模式时会从幅度、频率等方面对脉冲信号进行调制，使雷达跟踪其产生的虚假目标或虚假轨迹，进而影响雷达对目标的跟踪效果。转发模式下的干扰机所产生的欺骗干扰中最具有代表性的就是拖引欺骗干扰。

目标回波信号

   在不考虑线性调频和频率变化等因素影响的情况下，即，认为回波信号为单载频信号，则雷达接收到的目标回波信号的数学模型为：
$$S_R(t)=U_{R}cos[(w_c+w_d)(t-\frac{2R(t)}{c})]$$

距离波门拖引干扰

   当采取距离波门拖引干扰时，相对于正常的回波信号，干扰信号增加了一定的转发时延，因此，它的时域表达式如下：
$$J(t)=U_{J}cos[(w_c+w_d)(t-\frac{2R(t)}{c})-\Delta t]$$
   其中，$U_R$ 和 $U_J$分别为目标信号的幅度和干扰信号的幅度，并且满足 $U_J>U_R$, $w_c$为中心频率，$w_d$ 为回波信号的频移， $R(t)$为真实目标的距离， $\Delta t$为干扰信号相对于真实目标回波信号的延时。

速度波门拖引干扰

   当采取速度波门拖引干扰时，相对于正常的回波，干扰机对接收信号增加了一个多普勒频率偏移量 $\Delta w$，然后将其转发出去，因此，速度欺骗干扰的数学表达式如下：
$$J(t)=U_{J}cos[(w_c+w_d+\Delta w)(t-\frac{2R(t)}{c})]$$
   其中，$U_J$为干扰信号的幅度， $w_c$为中心频率，$w_d$ 为回波信号的频移， $\Delta w$为多普勒频率的偏移量。

距离-速度同步欺骗干扰

   在实际应用中，对于具有距离和速度能同时跟踪或检测的雷达来说，如果对其只采取距离或速度信息的欺骗，就可能被雷达识别出来，使干扰效果下降甚至失效，因此，需要对雷达实施一种更加有效的干扰方式，即，距离-速度同步欺骗，阻碍雷达的正常工作。

采样转发干扰

   数字射频存储(DRFM)干扰机的应答工作模式是一种新体制的欺骗工作模式，此模式下干扰机对 $s(t)$进行采样复制后对得到的信号脉冲段进行延时、幅度、频率或相位等方面的调制，可以产生包括间歇采样转发干扰、切片组合干扰和频谱弥散干扰的采样转发干扰。
   其中间歇采样干扰是一种基于天线收发分时体制的干扰信号，干扰机每次对 $s(t)$ 采样得到一个脉冲段进行转发，最终生成间歇采样干扰使雷达检测到多个假目标，一定条件下还可以产生压制效果。
   间歇采样转发干扰是使用脉宽为 $\tau$、采样周期为 $T_s$ 的矩形包络脉冲 $p(t)$对 $s(t)$ 进行周期性的间歇采样，采样结果为 $x_s(t)$，则采样信号表示如下：
$$p(t)=rect(\frac{t}{\tau })\sum _{-\infty }^{+\infty }\delta (t-n{T}_s)$$
$$x_n(t)=rect[\frac{t-(n-1)T_s}{\tau }]s(t)$$
$$x_s(t)=p(t)s(t)=\sum _{n=1}^N{x}_n(t)$$
   式中，$$rect(\frac{t}{\tau })=\{\begin{array}{rcl}1& & 0\le t\le \tau \\ 0& & others\end{array}$$

间歇采样直接转发信号

   间歇采样直接转发干扰（Interrupted Sampling and Direct Repeater Jamming，ISDJ）是将采样的子脉冲直接转发，等效于将采样信号延迟$\tau$后转发，可以表示为：
$$ISDJ(t)=x_s(t-\tau )$$

间歇采样重复转发信号

   间歇采样重复转发干扰（Interrupted Sampling and Repeat Repeater Jamming，ISRJ），是每次采样得到的子脉冲$x_n(t)$后，将其逐次延时 $k\tau$的时间长度进行转发， $k=1,2,\cdots ,M$, $M=\lfloor T_s/\tau \rfloor -1$，表示每个 $T_s$ 最多可转发 $x_n(t)$的次数，可以描述如下：
$$ISRJ(t)=\sum _{i_M=1}^M{x}_s(t-i_M\tau )$$

间歇采样循环转发信号

   间歇采样循环转发干扰（Interrupted Sampling and Circle Repeater Jamming，ISCJ）的原理是第一次采样得到子脉冲$x_1(t)$，转发$x_1(t)$，第二次采样得到$x_2(t)$，依次转发$x_2(t)$、$x_1(t)$，第三次转发$x_3(t)$、$x_2(t)$、$x_1(t)$，依次类推直到脉冲结束；若脉冲结束，则按后采先发的顺序转发之前的子脉冲，并删除最前面的一个子脉冲。整个过程将采样子脉冲依次延时 $\tau +k(T_s+\tau ),k=0,1,\cdots ,R-1,R=\min \{N,M\}$后转发，可建模为：
$$ISCJ(t)=\sum _{i_R=0}^{R-1}{x}_s(t-\tau -i_R(T_s+\tau ))$$

干扰信号的特征值

   雷达干扰信号与目标回波信号的区别以及各种干扰信号之间的区别首先会体现在信号的时间序列上，首先考虑信号时域波形的特征。除此之外，还可以从频域等方面分析。接下来从时域和频域两方面来介绍一些特征值。

时域特征

   不同类型的干扰信号，他们在时域波形的变化情况是各不相同的，因此，可以通过提取信号在时域的不同特征参数，作为干扰类型的识别依据。常用的时域特征参数有以下几种。

时域包络起伏度

   设信号 $x(t)=A(t)e^{j{w}_{0}t+\phi (t)}$，其离散时间采样序列为 $x(n)$，则信号瞬时包络的平方可表示为 $|x(n){|}^2=R{e}^2[x(n)]+I{m}^2[x(n)]$，瞬时包络平方 $|x(n){|}^2$的均值和方差分别为 $\mu$和$\sigma$， 其包络起伏度$R$为：
$$R={\sigma }^2/{\mu }^2$$

相关比参数

   假设接收信号为 $x(t)$，通过$B(t,\tau )=x(t)x^{\ast }(t+\tau )$可求得其瞬时自相关，在此基础上，可求得瞬时自相关的相关比参数：
$$S=min(N,P)/max(N,P)$$
   其中， N为$B(t,\tau )$中的值大于0的个数，而$P$为$B(t,\tau )$的值小于0的个数。

信号均值

   信号$x(n)$定义为：
$$\mu =E(x(n))$$

时域矩偏度

   时域矩偏度是一个三阶统计特征量，通常用它来描述一个时域分布的不对称程度，如果时域矩偏度系数大于0，则代表分布曲线的右侧比左侧长；若时域矩偏度系数小于0，则代表分布曲线的左侧比右侧长；若时域矩偏度系数等于0，则代表分布曲线对称。假设 $X$ 为随机变量，它的均值为 $\mu$,标准差为 $\sigma$，则时域矩偏度系数可用如下公式求得：
$$a_1=E(X-\mu {)}^3/{\sigma }^3$$

时域矩峰度

   时域矩峰度系数为一个四阶统计特征量，一般用它来表示一个时域分布的尖扁程度。当时域矩峰度小于3时，则代表一个扁峰存在；如果时域矩峰度大于3，则代表一个尖峰分布；如果时域矩峰度等于3，则近似服从正态分布。设随机变量$X$的均值为$\mu$，标准差为 $\sigma$，则它的时域矩峰度系数为：
$$a_2=E(X-\mu {)}^4/{\sigma }^4$$

频域特征

  功率谱表征了信号在频域的分布情况，对于不同类型的干扰信号，它们在频域的特性是不同的，因此，可以通过提取干扰信号在频域的多个特征参数，将它们作为干扰类型识别的依据。常用的频域的特征参数有以下几种：

加性白噪声因子1

  在理论分析与仿真中，所涉及的噪声为加性高斯白噪声，通过计算干扰信号的加性高斯白噪声因子，来获取表示信号频谱包络变化的特征参数。
  首先求出信号$x(t)$的功率谱$X(w)$，然后求取 $X(w)$ 的均值 $E_1$, 再求出 $X(w)$大于$E_1$的部分的均值 $E_2$，最后求出大于 $E_2$ 部分的 $X(w)$ 的均值 $E_3$，加性高斯白噪声因子的定义如下：
$$A_1=\frac{E_2-E_1}{E}$$

加性白噪声因子2

$$A_2=\frac{E_3-E_2}{E_1}$$

载波因子

  假设序列为 $x(n)$，对其进行离散傅里叶变换后为 $X(n),n\in \{1,2,\cdots ,N\}$，定义载波因子为：
$$R_2=\frac{max(X(n))}{sec(X(n))}$$
  其中，$max(X(n))$为 序列 $X(n)$的最大值，$sec(X(n))$为$X(n)$的次大值。在载波因子高于某个门限值时，可将其当做是载波信号，不同类型的干扰信号，在载波因子是各不相同的。

频域矩偏度

   频域矩偏度是一个三阶统计特征量，类似于时域矩偏度的计算方式，它反映的是功率谱密度分布的对称程度。对于信号 $x(t)$，功率谱为 $X(w)$，定义其频域矩偏度为：
$$a_3=E(X-\mu {)}^3/{\sigma }^3$$
   其中，$\mu$ 为 $X(w)$的均值， $\sigma$为 $X(w)$的标准差。

频域矩峰度

   频域矩峰度系数是一个四阶特征量，类似于时域矩峰度，它表示了信号的功率谱密度分布的陡峭程度。对于信号$x(t)$，其功率谱密度为 $X(w)$，其均值为 $\mu$，标准差为 $\sigma$，其频域矩峰度为：
$$a_4=E(X-\mu {)}^4/{\sigma }^4$$

MATLAB 仿真实现

MATLAB 实现见雷达有源干扰识别仿真

噪声干扰信号仿真

噪声调频信号的时频域特征

噪声调幅信号的时频域特征

射频噪声干扰的时频域特征

噪声卷积干扰的时频域特征

噪声乘积干扰的时频域特征

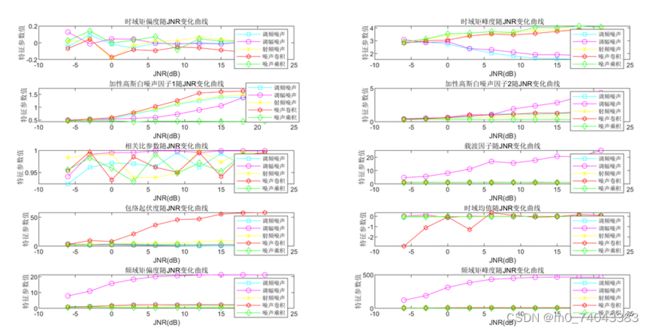
噪声干扰信号的各特征值随JNR的变化

噪声干扰信号的分类准确度随JNR的变化

拖引干扰仿真结果

略，具体见代码说明。

转发干扰仿真结果

略，具体见代码说明。