Leetcode Hot-100
参考
- hot100 视频
- leetcode讲解
【1-20】
1. 两数之和
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int,int> umap;
int i = 0;
for(int num:nums){
if(umap.find(target-num)==umap.end())
umap[num]=i;
else
return {umap[target-num],i};
i++;
}
return {};
}
};
2. 两数相加(链表数字相加)
解法一,报错,数据长度有限制, int long 都不能完全通过
求出来两个链表的数字,相加后,然后再合成链表返回
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
long long num1 = 0,num2 = 0;
long long mul1 = 1;
while(l1!=nullptr){
num1 = num1 + mul1 * l1->val;
mul1 *= 10;
l1 = l1->next;
}
mul1 = 1;
while(l2!=nullptr){
num2 = num2 + mul1 * l2->val;
mul1 *= 10;
l2 = l2->next;
}
long long res = num1 + num2;
if(res ==0 )
return new ListNode(0);
cout<<res;
ListNode* cur = new ListNode(0);
ListNode* dummy = new ListNode(-1);
dummy->next = cur;
while(res){
long long val = res%10;
ListNode* temp = new ListNode(val);
cur->next = temp;
cur = cur->next;
res = res/10;
}
return dummy->next->next;
}
};
这里的head tail两个指针,head只参与第一次节点创建,相当于dummy指针
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode *head = nullptr, *tail = nullptr;
int carry = 0;
while (l1 || l2) {
// 判断l1是否为空。
int n1 = l1 ? l1->val: 0;
// 判断l1是否为空。
int n2 = l2 ? l2->val: 0;
// 计算sum: carry为进位,初始为0
int sum = n1 + n2 + carry;
// 判断头节点是否非空:
if (!head) {
// 如果头节点空的话,首次添加节点
head = tail = new ListNode(sum % 10);
} else {
// 如果头节点非空的话,
tail->next = new ListNode(sum % 10);
tail = tail->next;
}
carry = sum / 10;
if (l1) {
l1 = l1->next;
}
if (l2) {
l2 = l2->next;
}
}
if (carry > 0) {
tail->next = new ListNode(carry);
}
return head;
}
};
3. 无重复的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
// labuladong解法
class Solution {
public:
int lengthOfLongestSubstring(string s) {
unordered_map<char, int> window;
int left = 0, right = 0;
int res = 0; // 记录结果
while (right < s.size()) {
char c = s[right];
right++;
// 进行窗口内数据的一系列更新
window[c]++;
// 判断左侧窗口是否要收缩
while (window[c] > 1) {
char d = s[left];
left++;
// 进行窗口内数据的一系列更新
window[d]--;
}
// 在这里更新答案
res = max(res, right - left);
}
return res;
}
};
5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
class Solution {
public:
string longestPalindrome(string s) {
string res="";
for(int i=0;i<s.size();i++){
string s1 = Palindrome(s,i,i);
string s2 = Palindrome(s,i,i+1);
res = res.size()>s1.size()?res:s1;
res = res.size()>s2.size()?res:s2;
}
return res;
}
string Palindrome(string& s, int l, int r) {
// 防止索引越界
while (l >= 0 && r < s.size()
&& s[l] == s[r]) {
// 向两边展开
l--; r++;
}
// 返回以 s[l] 和 s[r] 为中心的最长回文串
return s.substr(l + 1, r - l - 1);
}
};
5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
class Solution {
public:
string longestPalindrome(string s) {
string res="";
for(int i=0;i<s.size();i++){
string s1 = Palindrome(s,i,i);
string s2 = Palindrome(s,i,i+1);
res = res.size()>s1.size()?res:s1;
res = res.size()>s2.size()?res:s2;
}
return res;
}
string Palindrome(string& s, int l, int r) {
// 防止索引越界
while (l >= 0 && r < s.size()
&& s[l] == s[r]) {
// 向两边展开
l--; r++;
}
// 返回以 s[l] 和 s[r] 为中心的最长回文串
return s.substr(l + 1, r - l - 1);
}
};
6. 正则表达式匹配
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。
‘.’ 匹配任意单个字符
‘*’ 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。

正则表达式
解法一:动态规划
s 和 p 相互匹配的过程大致是,两个指针 i, j 分别在 s 和 p 上移动,如果最后两个指针都能移动到字符串的末尾,那么就匹配成功,反之则匹配失败。
正则表达算法问题只需要把住一个基本点:看 s[i] 和 p[j] 两个字符是否匹配,一切逻辑围绕匹配/不匹配两种情况展开即可。
动态规划算法的核心就是「状态」和「选择」,「状态」无非就是 i 和 j 两个指针的位置,「选择」就是模式串的 p[j] 选择匹配几个字符。
dp 函数的定义如下:
若 dp(s, i, p, j) = true,则表示 s[i…] 可以匹配 p[j…];若 dp(s, i, p, j) = false,则表示 s[i…] 无法匹配 p[j…]。
class Solution {
public:
// 备忘录
vector<vector<int>> memo;
bool isMatch(string s, string p) {
int m = s.size(), n = p.size();
memo = vector<vector<int>>(m, vector<int>(n, -1));
// 指针 i,j 从索引 0 开始移动
return dp(s, 0, p, 0);
}
/* 计算 p[j..] 是否匹配 s[i..] */
bool dp(string& s, int i, string& p, int j) {
int m = s.size(), n = p.size();
// base case
if (j == n) {
return i == m;
}
if (i == m) {
// 如果能匹配空串,一定是字符和 * 成对儿出现
if ((n - j) % 2 == 1) {
return false;
}
// 检查是否为 x*y*z* 这种形式
for (; j + 1 < n; j += 2) {
if (p[j + 1] != '*') {
return false;
}
}
return true;
}
// 查备忘录,防止重复计算
if (memo[i][j] != -1) {
return memo[i][j];
}
bool res = false;
if (s[i] == p[j] || p[j] == '.') {
// 匹配
if (j < n - 1 && p[j + 1] == '*') {
// 1.1 通配符匹配 0 次或多次
res = dp(s, i, p, j + 2)
|| dp(s, i + 1, p, j);
} else {
// 1.2 常规匹配 1 次
res = dp(s, i + 1, p, j + 1);
}
} else {
// 不匹配
if (j < n - 1 && p[j + 1] == '*') {
// 2.1 通配符匹配 0 次
res = dp(s, i, p, j + 2);
} else {
// 2.2 无法继续匹配
res = false;
}
}
// 将当前结果记入备忘录
memo[i][j] = res;
return res;
}
};
11. 盛最多水的容器

用 left 和 right 两个指针从两端向中心收缩,一边收缩一边计算 [left, right] 之间的矩形面积,取最大的面积值即是答案。
class Solution {
public:
int maxArea(vector<int>& height) {
int l = 0, r = height.size() - 1;
int ans = 0;
while (l < r) {
int area = min(height[l], height[r]) * (r - l);
ans = max(ans, area);
if (height[l] <= height[r]) {
++l;
}
else {
--r;
}
}
return ans;
}
};
15. 三数之和
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> result;
sort(nums.begin(), nums.end());
// 找出a + b + c = 0
// a = nums[i], b = nums[left], c = nums[right]
for (int i = 0; i < nums.size(); i++) {
// 排序之后如果第一个元素已经大于零,那么无论如何组合都不可能凑成三元组,直接返回结果就可以了
if (nums[i] > 0) {
return result;
}
// 正确去重方法
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
int left = i + 1;
int right = nums.size() - 1;
while (right > left) {
if (nums[i] + nums[left] + nums[right] > 0) {
right--;
// 当前元素不合适了,可以去重
while (left < right && nums[right] == nums[right + 1]) right--;
} else if (nums[i] + nums[left] + nums[right] < 0) {
left++;
// 不合适,去重
while (left < right && nums[left] == nums[left - 1]) left++;
} else {
result.push_back(vector<int>{nums[i], nums[left], nums[right]});
// 去重逻辑应该放在找到一个三元组之后
while (right > left && nums[right] == nums[right - 1]) right--;
while (right > left && nums[left] == nums[left + 1]) left++;
// 找到答案时,双指针同时收缩
right--;
left++;
}
}
}
return result;
}
};
17. 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
// 版本一
class Solution {
private:
const string letterMap[10] = {
"", // 0
"", // 1
"abc", // 2
"def", // 3
"ghi", // 4
"jkl", // 5
"mno", // 6
"pqrs", // 7
"tuv", // 8
"wxyz", // 9
};
public:
vector<string> result;
string s;
void backtracking(const string& digits, int index) {
if (index == digits.size()) {
result.push_back(s);
return;
}
int digit = digits[index] - '0'; // 将index指向的数字转为int
string letters = letterMap[digit]; // 取数字对应的字符集
for (int i = 0; i < letters.size(); i++) {
s.push_back(letters[i]); // 处理
backtracking(digits, index + 1); // 递归,注意index+1,一下层要处理下一个数字了
s.pop_back(); // 回溯
}
}
vector<string> letterCombinations(string digits) {
s.clear();
result.clear();
if (digits.size() == 0) {
return result;
}
backtracking(digits, 0);
return result;
}
};
19. 删除链表的倒数第 N 个结点
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* dummy = new ListNode(0,head);
ListNode* first = dummy;
ListNode* second = dummy;
for(int i =0;i<n+1;i++){
first = first->next;
}
while(first!=nullptr){
first = first->next;
second = second->next;
}
second->next = second->next->next;
return dummy->next;
}
};
20. 有效的括号
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
class Solution {
public:
bool isValid(string s) {
// 注意哈希字典的初始化
unordered_map<char,int> m{{'(',1},{'[',2},{'{',3},
{')',4},{']',5},{'}',6}};
stack<char> st;
bool istrue=true;
for(char c:s){
int flag=m[c];
if(flag>=1&&flag<=3) st.push(c);
else if(!st.empty()&&m[st.top()]==flag-3) st.pop();
else {istrue=false;break;}
}
if(!st.empty()) istrue=false;
return istrue;
}
};
21. 合并两个有序链表
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
ListNode* preHead = new ListNode(-1);
ListNode* prev = preHead;
while (l1 != nullptr && l2 != nullptr) {
if (l1->val < l2->val) {
prev->next = l1;
l1 = l1->next;
} else {
prev->next = l2;
l2 = l2->next;
}
prev = prev->next;
}
// 合并后 l1 和 l2 最多只有一个还未被合并完
// 我们直接将链表末尾指向未合并完的链表即可
prev->next = l1 == nullptr ? l2 : l1;
return preHead->next;
}
};
22. 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
输入:n = 3
输出:[“((()))”,“(()())”,“(())()”,“()(())”,“()()()”]
class Solution {
public:
vector<string> generateParenthesis(int n) {
if (n == 0) return {};
// 记录所有合法的括号组合
vector<string> res;
// 回溯过程中的路径
string track;
// 可用的左括号和右括号数量初始化为 n
backtrack(n, n, track, res);
return res;
}
// 可用的左括号数量为 left 个,可用的右括号数量为 rgiht 个
void backtrack(int left, int right,
string& track, vector<string>& res) {
// 若左括号剩下的多,说明不合法
if (right < left) return;
// 数量小于 0 肯定是不合法的
if (left < 0 || right < 0) return;
// 当所有括号都恰好用完时,得到一个合法的括号组合
if (left == 0 && right == 0) {
res.push_back(track);
return;
}
// 尝试放一个左括号
track.push_back('('); // 选择
backtrack(left - 1, right, track, res);
track.pop_back(); // 撤消选择
// 尝试放一个右括号
track.push_back(')'); // 选择
backtrack(left, right - 1, track, res);
track.pop_back(); // 撤消选择
}
};
23. 合并K个升序链表
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
class cmp {
public:
bool operator()(const ListNode* a,const ListNode* b) {
return a->val > b->val;
}
};
class Solution {
public:
priority_queue<ListNode*,vector<ListNode*>,cmp> q;
ListNode* mergeKLists(vector<ListNode*>& lists) {
ListNode* dummy = new ListNode(-1);
ListNode* p = dummy;
for (ListNode* node: lists) {//将每多个链表的 头节点 放入优先队列
if (node) q.push(node);
}
while (!q.empty()) {
ListNode* cur = q.top();
q.pop();
p->next = cur;
if(cur->next!=nullptr){
q.push(cur->next);
}
p = p->next;
}
return dummy->next;
}
};
31. 下一个排列
注意到下一个排列总是比当前排列要大,除非该排列已经是最大的排列。我们希望找到一种方法,能够找到一个大于当前序列的新序列,且变大的幅度尽可能小。具体地:
我们需要将一个左边的「较小数」与一个右边的「较大数」交换,以能够让当前排列变大,从而得到下一个排列。
同时我们要让这个「较小数」尽量靠右,而「较大数」尽可能小。当交换完成后,「较大数」右边的数需要按照升序重新排列。这样可以在保证新排列大于原来排列的情况下,使变大的幅度尽可能小。

class Solution {
public:
void nextPermutation(vector<int>& nums) {
int n = nums.size();
int i = n - 2; // a[i] > a[i+1]
while(i>=0 && nums[i]>=nums[i+1]) i--;
if(i==-1){
reverse(nums.begin(),nums.end());
return;
}
int j = n-1;
while(nums[j]<=nums[i]) j--;
swap(nums[i],nums[j]);
reverse(nums.begin()+i+1,nums.end());
}
};
32. 最长有效括号
给你一个只包含 ‘(’ 和 ‘)’ 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
输入:s = “(()”
输出:2
解释:最长有效括号子串是 “()”
( +1 ) -1 首次总和<0
class Solution {
public:
int longestValidParentheses(string s) {
int n = s.size();
stack<int> stk;// 存元素下表
stk.push(-1); // 作为极端情况下的外边界
int ret = 0;
for(int i = 0; i < n; i++){
if(s[i] == '('){
stk.push(i);
}else{
// 如果为 )的话
// 如果栈顶为-1 代表为空 || 如果栈顶的索引在字符串里面为 ) 两种情况不匹配 直接将新的)压栈
if(stk.top()==-1 || s[stk.top()]==')'){
stk.push(i);
}else if ( s[stk.top()]=='('){
// 如果栈顶元素为 ( 代表匹配 弹出该元素,用该元素前面的元素计算 与i的距离,并更新最大有效长度
stk.pop();//[1,i]
int b = stk.top();
ret = max(ret,i-b);
}
}
}
return ret;
}
};
33. 搜索旋转排序数组
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
mid分割后肯定有一部分是有序的,一部分可能有序可能无序
将数组一分为二,其中一定有一个是有序的,另一个可能是有序,也能是部分有序。
此时有序部分用二分法查找。无序部分再一分为二,其中一个一定有序,另一个可能有序,可能无序。就这样循环.
class Solution {
public:
int search(vector<int>& nums, int target) {
int n = (int)nums.size();
if (!n) {
return -1;
}
if (n == 1) {
return nums[0] == target ? 0 : -1;
}
int l = 0, r = n - 1;
while (l <= r) {
int mid = (l + r) / 2;
if (nums[mid] == target) return mid;
if (nums[0] <= nums[mid]) {
if (nums[0] <= target && target < nums[mid]) {
r = mid - 1;
} else {
l = mid + 1;
}
} else {
if (nums[mid] < target && target <= nums[n - 1]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
}
return -1;
}
};
39. 组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
if(candidates.size()==0){
return res;
}
backtrack(candidates,0,target,0);
return res;
}
void backtrack(vector<int>& candidates, int start,int target,int sum){
if(target==sum){
res.push_back(path);
return;
}
if(sum>target){return;}
for(int i =start;i<candidates.size();i++){
path.push_back(candidates[i]);
sum+=candidates[i];
backtrack(candidates,i,target,sum);
sum-=candidates[i];
path.pop_back();
}
}
};
42. 接雨水
解法1: 双指针
class Solution {
public:
int trap(vector<int>& height) {
int n = height.size();
if (n == 0) {
return 0;
}
vector<int> leftMax(n);
leftMax[0] = height[0];
for (int i = 1; i < n; ++i) {
leftMax[i] = max(leftMax[i - 1], height[i]);
}
vector<int> rightMax(n);
rightMax[n - 1] = height[n - 1];
for (int i = n - 2; i >= 0; --i) {
rightMax[i] = max(rightMax[i + 1], height[i]);
}
int ans = 0;
for (int i = 0; i < n; ++i) {
ans += min(leftMax[i], rightMax[i]) - height[i];
}
return ans;
}
};
解法二:单调栈
class Solution {
public:
int trap(vector<int>& height) {
if (height.size() <= 2) return 0; // 可以不加
stack<int> st; // 存着下标,计算的时候用下标对应的柱子高度
st.push(0);
int sum = 0;
for (int i = 1; i < height.size(); i++) {
if (height[i] < height[st.top()]) { // 情况一
st.push(i);
} if (height[i] == height[st.top()]) { // 情况二
st.pop(); // 其实这一句可以不加,效果是一样的,但处理相同的情况的思路却变了。
st.push(i);
} else { // 情况三
while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while
int mid = st.top();
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1; // 注意减一,只求中间宽度
sum += h * w;
}
}
st.push(i);
}
}
return sum;
}
};
46. 全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
class Solution {
public:
vector<vector<int>> result;
vector<int> path;
void backtracking (vector<int>& nums, vector<bool>& used) {
// 此时说明找到了一组
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
for (int i = 0; i < nums.size(); i++) {
if (used[i] == true) continue; // path里已经收录的元素,直接跳过
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
vector<vector<int>> permute(vector<int>& nums) {
result.clear();
path.clear();
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return result;
}
};
48. 旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
int m = matrix.size();
int n = matrix[0].size();
// 先沿对角线反转二维矩阵
for(int i=0;i<=m-1;i++){
for(int j =i;j<=n-1;j++){
int temp = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = temp;
}
}
// 然后反转二维矩阵的每一行
for(int i = 0;i<m;i++){
int left = 0,right = matrix[0].size()-1;
// 反转一维数组
while(left<right){
int temp = matrix[i][left];
matrix[i][left] = matrix[i][right];
matrix[i][right] = temp;
left++;
right--;
}
}
}
};
【21-40】
49. 字母异位词分组
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的字母得到的一个新单词,所有源单词中的字母通常恰好只用一次。
输入: strs = [“eat”, “tea”, “tan”, “ate”, “nat”, “bat”]
输出: [[“bat”],[“nat”,“tan”],[“ate”,“eat”,“tea”]]
解法一:哈希的方法
class Solution {
public:
vector<vector<string>> groupAnagrams(vector<string>& strs) {
unordered_map<string,vector<string>> umap;
for(const auto& s:strs){
auto key = s;
sort(key.begin(),key.end());
umap[key].push_back(s);
}
vector<vector<string>> res;
for(const auto& vec:umap){
res.push_back(vec.second);
}
return res;
}
};
53. 最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
解法一:贪心的思想
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int result = INT32_MIN;
int count = 0;
for (int i = 0; i < nums.size(); i++) {
count += nums[i];
if (count > result) { // 取区间累计的最大值(相当于不断确定最大子序终止位置)
result = count;
}
if (count <= 0) count = 0; // 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和
}
return result;
}
};
解法二: 动态规划的思想
以 nums[i] 为结尾的「最大子数组和」为 dp[i]。
dp[i] 有两种「选择」,要么与前面的相邻子数组连接,形成一个和更大的子数组;要么不与前面的子数组连接,自成一派,自己作为一个子数组。
在这两种选择中择优,就可以计算出最大子数组,而且空间复杂度还有优化空间,见详细题解。
class Solution {
public int maxSubArray(int[] nums) {
int n = nums.length;
if (n == 0) return 0;
int[] dp = new int[n];
// base case
// 第一个元素前面没有子数组
dp[0] = nums[0];
// 状态转移方程
for (int i = 1; i < n; i++) {
dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);
}
// 得到 nums 的最大子数组
int res = Integer.MIN_VALUE;
for (int i = 0; i < n; i++) {
res = Math.max(res, dp[i]);
}
return res;
}
}
// 详细解析参见:
// https://labuladong.github.io/article/?qno=53
55. 跳跃游戏
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
class Solution {
public:
bool canJump(vector<int>& nums) {
int cover = 0;
if (nums.size() == 1) return true; // 只有一个元素,就是能达到
for (int i = 0; i <= cover; i++) { // 注意这里是小于等于cover - 下标索引
cover = max(i + nums[i], cover);
if (cover >= nums.size() - 1) return true; // 说明可以覆盖到终点了
}
return false;
}
};
56. 合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
class Solution {
public:
// intervals 形如 [[1,3],[2,6]...]
vector<vector<int>> merge(vector<vector<int>>& intervals) {
// # 按区间的 start 升序排列
sort(intervals.begin(),intervals.end(),[](vector<int> & a,vector<int>& b){
return a[0] < b[0];
});
vector<vector<int>> res;
res.push_back(intervals[0]);
// # res 中最后一个元素的引用
for(int i = 1; i < intervals.size(); i++){
vector<int> cur = intervals[i];
if(cur[0] <= res.back()[1]){
// # 找到最大的 end
res.back()[1] = max(cur[1],res.back()[1]);
}else{
// 处理下一个待合并区间
res.push_back(cur);
}
}
return res;
}
};
62. 不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
- dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- dp[i][j] = dp[i - 1][j] + dp[i][j - 1],因为dp[i][j]只有这两个方向过来。
- 首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,那么dp[0][j]也同理。
- dp[i][j]都是从其上方和左方推导而来,那么从左到右一层一层遍历就可以了。
- 举例推导dp数组
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};
64. 最小路径和
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
解法一:暴力搜索 : 只过了23个用例
class Solution {
public:
int res = INT_MAX;
int minPathSum(vector<vector<int>>& grid) {
dfs(grid,0,0,0);
return res;
}
void dfs(vector<vector<int>>& grid,int i,int j,int sum){
int m = grid.size(),n = grid[0].size();
if(i>=m || j>=n) return;
sum += grid[i][j];
if(i==m-1 && j == n-1) res = sum < res? sum : res;
dfs(grid,i+1,j,sum);
dfs(grid,i,j+1,sum);
}
};
解法二: 动态规划
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
if (grid.size() == 0 || grid[0].size() == 0) {
return 0;
}
int rows = grid.size(), columns = grid[0].size();
auto dp = vector < vector <int> > (rows, vector <int> (columns));
dp[0][0] = grid[0][0];
// 初始化 第一列
for (int i = 1; i < rows; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
// 初始化 第一行
for (int j = 1; j < columns; j++) {
dp[0][j] = dp[0][j - 1] + grid[0][j];
}
// 遍历递推
for (int i = 1; i < rows; i++) {
for (int j = 1; j < columns; j++) {
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
return dp[rows - 1][columns - 1];
}
};
70. 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
动态规划的思路
// 版本一
class Solution {
public:
int climbStairs(int n) {
if (n <= 1) return n; // 因为下面直接对dp[2]操作了,防止空指针
vector<int> dp(n + 1);
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) { // 注意i是从3开始的
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
完全背包的思路:
dp[i]有几种来源,dp[i - 1],dp[i - 2],dp[i - 3] 等等,即:dp[i - j] dp[i] += dp[i - j]
0070.爬楼梯完全背包版本.html#_70-爬楼梯
class Solution {
public:
int climbStairs(int n) {
vector<int> dp(n + 1, 0);
dp[0] = 1;
for (int i = 1; i <= n; i++) { // 遍历背包
for (int j = 1; j <= 2; j++) { // 遍历物品
if (i - j >= 0) dp[i] += dp[i - j];
}
}
return dp[n];
}
};
72. 编辑距离
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
输入:word1 = “horse”, word2 = “ros”
输出:3
解释:
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)
-
dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
-
if (word1[i - 1] == word2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
}
else {
dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}
dp[i][0] :以下标i-1为结尾的字符串word1,和空字符串word2,最近编辑距离为dp[i][0]。
那么dp[i][0]就应该是i,对word1里的元素全部做删除操作,即:dp[i][0] = i;
同理dp[0][j] = j;
- 确定遍历顺序
所以在dp矩阵中一定是从左到右从上到下去遍历。
class Solution {
public:
int minDistance(string word1, string word2) {
vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
for (int i = 1; i <= word1.size(); i++) {
for (int j = 1; j <= word2.size(); j++) {
if (word1[i - 1] == word2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1];
}
else {
dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}
}
}
return dp[word1.size()][word2.size()];
}
};
75. 颜色分类
给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库的sort函数的情况下解决这个问题。
class Solution {
public:
void sortColors(vector<int>& nums) {
int n = nums.size();
int left = 0;
int right = n - 1;
for(int i = 0;i < nums.size();){
if(nums[i]==2){
//在右侧寻找坑位
while(right>i && nums[right]==2) right--;
if(right>i){
//如果在右侧找到了坑位
swap(nums[right],nums[i]);
right--; //挪动坑位,i不动
}else{
// 未找到坑位
break;
}
}else if(nums[i]==0){
//在左侧寻找坑位
while(left<i&&nums[left]==0) left++;
if(left<i){
//找到坑位
swap(nums[left],nums[i]);
left++;
}else{
//整个左侧都是0.left.i 右移
left++,i++;
}
}else{
i++;
}
}
}
};
76. 最小覆盖子串
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 “”
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串,我们保证它是唯一的答案。
输入:s = “ADOBECODEBANC”, t = “ABC”
输出:“BANC”
解法一: 哈希 + 滑动窗口
class Solution {
public:
string minWindow(string s, string t) {
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
int left = 0, right = 0;
int valid = 0;
// 记录最小覆盖子串的起始索引及长度
int start = 0, len = INT_MAX;
while (right < s.size()) {
// c 是将移入窗口的字符
char c = s[right];
// 右移窗口
right++;
// 进行窗口内数据的一系列更新
if (need.count(c)) {
window[c]++;
if (window[c] == need[c]) // 可能存在window[c]大于need字符的情况
valid++;
}
// 判断左侧窗口是否要收缩
while (valid == need.size()) {
// 在这里更新最小覆盖子串
if (right - left < len) {
start = left;
len = right - left;
}
// d 是将移出窗口的字符
char d = s[left];
// 左移窗口
left++;
// 进行窗口内数据的一系列更新
if (need.count(d)) {
if (window[d] == need[d])
valid--;
window[d]--;
}
}
}
// 返回最小覆盖子串
return len == INT_MAX ?"" : s.substr(start, len);
}
};
78. 子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& nums, int startIndex) {
result.push_back(path); // 收集子集,要放在终止添加的上面,否则会漏掉自己
if (startIndex >= nums.size()) { // 终止条件可以不加
return;
}
for (int i = startIndex; i < nums.size(); i++) {
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
public:
vector<vector<int>> subsets(vector<int>& nums) {
result.clear();
path.clear();
backtracking(nums, 0);
return result;
}
};
79. 单词搜索
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
class Solution {
public:
bool check(vector<vector<char>>& board, vector<vector<int>>& visited, int i, int j, string& s, int k) {
if (board[i][j] != s[k]) {
return false;
} else if (k == s.length() - 1) {
return true;
}
visited[i][j] = true;
vector<pair<int, int>> directions{{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
bool result = false;
for (const auto& dir: directions) {
int newi = i + dir.first, newj = j + dir.second;
if (newi >= 0 && newi < board.size() && newj >= 0 && newj < board[0].size()) {
if (!visited[newi][newj]) {
bool flag = check(board, visited, newi, newj, s, k + 1);
if (flag) {
result = true;
break;
}
}
}
}
visited[i][j] = false;
return result;
}
bool exist(vector<vector<char>>& board, string word) {
int h = board.size(), w = board[0].size();
vector<vector<int>> visited(h, vector<int>(w));
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
bool flag = check(board, visited, i, j, word, 0);
if (flag) {
return true;
}
}
}
return false;
}
};
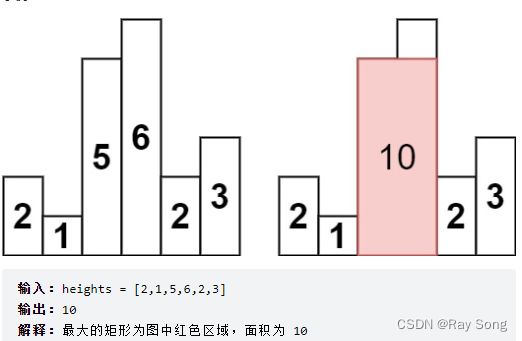
84. 柱状图中最大的矩形
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
单调栈解法
0084.柱状图中最大的矩形.html#单调栈
情况一:当前遍历的元素heights[i]小于栈顶元素heights[st.top()]的情况
情况二:当前遍历的元素heights[i]等于栈顶元素heights[st.top()]的情况
情况三:当前遍历的元素heights[i]大于栈顶元素heights[st.top()]的情况
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> st;
heights.insert(heights.begin(), 0); // 数组头部加入元素0
heights.push_back(0); // 数组尾部加入元素0
st.push(0);
int result = 0;
// 第一个元素已经入栈,从下标1开始
for (int i = 1; i < heights.size(); i++) {
// 注意heights[i] 是和heights[st.top()] 比较 ,st.top()是下标
if (heights[i] > heights[st.top()]) {
st.push(i);
} else if (heights[i] == heights[st.top()]) {
st.pop(); // 这个可以加,可以不加,效果一样,思路不同
st.push(i);
} else {
while (heights[i] < heights[st.top()]) { // 注意是while
int mid = st.top();
st.pop();
int left = st.top();
int right = i;
int w = right - left - 1;
int h = heights[mid];
result = max(result, w * h);
}
st.push(i);
}
}
return result;
}
};
85. 最大矩形
给定一个仅包含 0 和 1 、大小为 rows x cols 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
以矩阵的每一行为x轴,
class Solution {
public:
int maximalRectangle(vector<vector<char>>& matrix) {
int row = matrix.size();
if (row == 0)
return 0;
int col = matrix[0].size();
vector<int> heights(col,0);
// heights[col] = -1;
int res = 0;
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
heights[j] = matrix[i][j] == '1' ? heights[j] + matrix[i][j] - '0' : 0;
}
res = max(res, largestRectangleArea(heights));
}
return res;
}
int largestRectangleArea(vector<int> heights) {
stack<int> st;
heights.insert(heights.begin(), 0); // 数组头部加入元素0
heights.push_back(0); // 数组尾部加入元素0
st.push(0);
int result = 0;
// 第一个元素已经入栈,从下标1开始
for (int i = 1; i < heights.size(); i++) {
// 注意heights[i] 是和heights[st.top()] 比较 ,st.top()是下标
if (heights[i] > heights[st.top()]) {
st.push(i);
} else if (heights[i] == heights[st.top()]) {
st.pop(); // 这个可以加,可以不加,效果一样,思路不同
st.push(i);
} else {
while (heights[i] < heights[st.top()]) { // 注意是while
int mid = st.top();
st.pop();
int left = st.top();
int right = i;
int w = right - left - 1;
int h = heights[mid];
result = max(result, w * h);
}
st.push(i);
}
}
return result;
}
};
94. 二叉树的中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> res;
vector<int> inorderTraversal(TreeNode* root) {
tranverse(root);
return res;
}
void tranverse(TreeNode* root){
if(root==nullptr){
return;
}
tranverse(root->left);
res.push_back(root->val);
tranverse(root->right);
}
};
96. 不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。

思路:
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
- dp[i] : 1到i为节点组成的二叉搜索树的个数为dp[i]。
- dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
j相当于是头结点的元素,从1遍历到i为止。
所以递推公式:dp[i] += dp[j - 1] * dp[i - j]; ,
j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量
- dp[0] = 1
- 顺序遍历 两个for循环
- 举例
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n + 1);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
};
98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
class Solution {
private:
vector<int> vec;
void traversal(TreeNode* root) {
if (root == NULL) return;
traversal(root->left);
vec.push_back(root->val); // 将二叉搜索树转换为有序数组
traversal(root->right);
}
public:
bool isValidBST(TreeNode* root) {
vec.clear(); // 不加这句在leetcode上也可以过,但最好加上
traversal(root);
for (int i = 1; i < vec.size(); i++) {
// 注意要小于等于,搜索树里不能有相同元素
if (vec[i] <= vec[i - 1]) return false;
}
return true;
}
};
101. 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
class Solution {
public:
bool compare(TreeNode* left, TreeNode* right) {
// 首先排除空节点的情况
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
// 排除了空节点,再排除数值不相同的情况
else if (left->val != right->val) return false;
// 此时就是:左右节点都不为空,且数值相同的情况
// 此时才做递归,做下一层的判断
bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右
bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左
bool isSame = outside && inside; // 左子树:中、 右子树:中 (逻辑处理)
return isSame;
}
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
return compare(root->left, root->right);
}
};
102. 二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
class Solution {
public:
vector<vector<int>> res;
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*> q;
//需要加判断 判断是否为空 root节点
if(root==nullptr){
return res;
}
q.push(root);
while(!q.empty()){
int n = q.size();
vector<int> temp;
for(int i =0;i<n;i++){
TreeNode* cur = q.front();
q.pop();
temp.push_back(cur->val);
// 需要判断当前cur是否为空
if(cur->left!=nullptr){
q.push(cur->left);
}
if(cur->right!=nullptr){
q.push(cur->right);
}
}
res.push_back(temp);
}
return res;
}
};
104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
class Solution {
public:
int res = 0;
int depth = 0;
int maxDepth(TreeNode* root) {
tranverse(root);
return res;
}
void tranverse(TreeNode* root){
if(root ==nullptr){
if(res<depth){
res = depth;
}
return;
}
this->depth++;
tranverse(root->left);
tranverse(root->right);
this->depth--;
}
};
【41-50】
105. 前序遍历和中序遍历重建二叉树
class Solution {
public:
unordered_map<int,int> umap;
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
for (int i = 0; i < inorder.size(); i++) umap[inorder[i]] = i;
return build(preorder, 0, preorder.size() - 1,
inorder, 0, inorder.size() - 1);
}
TreeNode* build(vector<int>& preorder ,int preStart, int preEnd,
vector<int>& inorder,int inStart,int inEnd){
if(preStart > preEnd) return nullptr;
// root 节点对应的值就是后序遍历数组的最后一个元素
int rootVal = preorder[preStart];
// rootVal 在中序遍历数组中的索引
int index = umap[rootVal];
// 左子树的节点个数
int leftSize = index - inStart;
// 先构造出当前根节点
TreeNode* root = new TreeNode(rootVal);
// 递归构造左右子树
root->left = build(preorder, preStart + 1, preStart + leftSize,
inorder, inStart, index - 1);
root->right = build(preorder, preStart + leftSize + 1, preEnd,
inorder, index + 1, inEnd);
return root;
}
};
114. 二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表:
展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。
class Solution {
public:
void flatten(TreeNode* root) {
tranverse(root);
}
// 右子树移动到左子树下
void tranverse(TreeNode* root){
if(root==nullptr){
return;
}
tranverse(root->left);
tranverse(root->right);
// 1.左右子树已经被拉伸成一条链表
TreeNode* left = root->left;
TreeNode* right = root->right;
// 2.左子树作为右子树
root->left=nullptr;
root->right = left;
// 3.将原先右子树接到当前右子树【末端】
TreeNode* p = root;
while(p->right!=nullptr){
p = p->right;
}
p->right = right;
}
};
121. 买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
-
dp[i][0] 表示第i天持有股票所得最多现金 dp[i][1] 表示第i天不持有股票所得最多现金
其实一开始现金是0,那么加入第i天买入股票现金就是 -prices[i], 这是一个负数。
dp[i][0] = max(dp[i - 1][0], -prices[i])
如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来:
- 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金
即:dp[i - 1][0] - 第i天买入股票,所得现金就是买入今天的股票后所得现金
即:-prices[i]
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
如果第i天不持有股票即dp[i][1], 也可以由两个状态推出来
- 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金
即:dp[i - 1][1] - 第i天卖出股票,所得现金就是按照今天股票佳价格卖出后所得现金
即:prices[i] + dp[i - 1][0]
- dp[0][0] -= prices[0]; dp[0][1] = 0;
- 从递推公式可以看出dp[i]都是有dp[i - 1]推导出来的,那么一定是从前向后遍历
class Solution {
public:
int maxProfit(vector<int>& prices) {
int len = prices.size();
if (len == 0) return 0;
vector<vector<int>> dp(len, vector<int>(2));
dp[0][0] -= prices[0];
dp[0][1] = 0;
for (int i = 1; i < len; i++) {
dp[i][0] = max(dp[i - 1][0], -prices[i]);
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
}
return dp[len - 1][1];
}
};
124. 二叉树中的最大路径和
路径 被定义为一条从树中任意节点出发,沿父节点-子节点连接,达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
class Solution {
public:
int res = INT_MIN;
int maxPathSum(TreeNode* root) {
if(root==nullptr){
return 0;
}
oneSideMax(root);
return res;
}
// 定义:计算从根节点 root 为起点的最大单边路径和
int oneSideMax(TreeNode* root){
if(root==nullptr){
return 0;
}
int lmax = max(0,oneSideMax(root->left));
int rmax = max(0,oneSideMax(root->right));
// 后序遍历位置,顺便更新最大路径和
int sums = lmax+rmax+root->val;
res = max(res,sums);
// 实现函数定义,左右子树的最大单边路径和加上根节点的值
// 就是从根节点 root 为起点的最大单边路径和
return max(lmax,rmax)+root->val;
}
};
128. 最长连续序列
不用考虑顺序,找出一些值,重新排列,让他们是连续的。要求O(n)时间复杂度。
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
最简单直接sort一下,然后排列找。
使用哈希进行标志,对每个元素向两边扩充判断,访问过进行标记,线性的算法
class Solution {
public:
int longestConsecutive(vector<int>& nums) {
unordered_map<int,int> data;
for(int x : nums) data[x] = 1;
int ret = 0;
for(auto& p : data)
if(p.second){
int val = p.first,len = 1;
for(int i = 1; data.count(val-i) && data[val-i];i++)
len++, data[val-i] = 0;
for(int i = 1; data.count(val+i) && data[val+i];i++)
len++,data[val+i] = 0;
ret = max(ret,len);
}
return ret;
}
};
136. 只出现一次的数字
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
class Solution {
public:
int singleNumber(vector<int>& nums) {
int res = 0;
for(int num : nums){
res ^= num;
}
return res;
}
};
139. 单词拆分
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。
输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以由 “apple” “pen” “apple” 拼接成。
注意,你可以重复使用字典中的单词。
解法:
单词就是物品,字符串s就是背包,单词能否组成字符串s,就是问物品能不能把背包装满。
- dp[i] : 字符串长度为i的话,dp[i]为true,表示可以拆分为一个或多个在字典中出现的单词。
- 如果确定dp[j] 是true,且 [j, i] 这个区间的子串出现在字典里,那么dp[i]一定是true。(j < i )。
所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。 - dp[0]就是递归的根基,dp[0]一定要为true
- 遍历背包放在外循环,将遍历物品放在内循环。内循环从前到后。
本题还有特殊性,因为是要求子串,最好是遍历背包放在外循环,将遍历物品放在内循环。
如果要是外层for循环遍历物品,内层for遍历背包,就需要把所有的子串都预先放在一个容器里。
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
vector<bool> dp(s.size() + 1, false);
dp[0] = true;
for (int i = 1; i <= s.size(); i++) { // 遍历背包
for (int j = 0; j < i; j++) { // 遍历物品
string word = s.substr(j, i - j); //substr(起始位置,截取的个数)
if (wordSet.find(word) != wordSet.end() && dp[j]) {
dp[i] = true;
}
}
}
return dp[s.size()];
}
};
141. 环形链表
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
class Solution {
public:
bool hasCycle(ListNode *head) {
ListNode* slow = head;
ListNode* fast = head;
while(fast!=NULL&&fast->next!=NULL){
fast = fast->next->next;
slow = slow->next;
if(fast==slow){
return true;
}
}
return false;
}
};
【51-60】
142. 环形链表 II
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode * fast = head;
ListNode * slow = head;
// 在环中第一次相遇后退出
while(fast!=NULL&&fast->next!=NULL){
fast =fast->next->next;
slow = slow->next;
if(fast==slow){
break;
}
}
// 然后将一个指针放在头节点,开始寻找环的入口
// if语句段放的位置容易出错
if(fast == NULL ||fast->next==NULL){
return NULL;
}
slow = head;
while(slow!=fast){
fast = fast->next;
slow = slow->next;
}
return slow;
}
};
146. LRU缓存
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
struct DLinkedNode {
int key, value;
DLinkedNode* prev;
DLinkedNode* next;
DLinkedNode(): key(0), value(0), prev(nullptr), next(nullptr) {}
DLinkedNode(int _key, int _value): key(_key), value(_value), prev(nullptr), next(nullptr) {}
};
class LRUCache {
private:
unordered_map<int, DLinkedNode*> cache;
DLinkedNode* head;
DLinkedNode* tail;
int size;
int capacity;
public:
LRUCache(int _capacity): capacity(_capacity), size(0) {
// 使用伪头部和伪尾部节点
head = new DLinkedNode();
tail = new DLinkedNode();
head->next = tail;
tail->prev = head;
}
int get(int key) {
if (!cache.count(key)) {
return -1;
}
// 如果 key 存在,先通过哈希表定位,再移到头部
DLinkedNode* node = cache[key];
moveToHead(node);
return node->value;
}
void put(int key, int value) {
if (!cache.count(key)) {
// 如果 key 不存在,创建一个新的节点
DLinkedNode* node = new DLinkedNode(key, value);
// 添加进哈希表
cache[key] = node;
// 添加至双向链表的头部
addToHead(node);
++size;
if (size > capacity) {
// 如果超出容量,删除双向链表的尾部节点
DLinkedNode* removed = removeTail();
// 删除哈希表中对应的项
cache.erase(removed->key);
// 防止内存泄漏
delete removed;
--size;
}
}
else {
// 如果 key 存在,先通过哈希表定位,再修改 value,并移到头部
DLinkedNode* node = cache[key];
node->value = value;
moveToHead(node);
}
}
void addToHead(DLinkedNode* node) {
node->prev = head;
node->next = head->next;
head->next->prev = node;
head->next = node;
}
void removeNode(DLinkedNode* node) {
node->prev->next = node->next;
node->next->prev = node->prev;
}
void moveToHead(DLinkedNode* node) {
removeNode(node);
addToHead(node);
}
DLinkedNode* removeTail() {
DLinkedNode* node = tail->prev;
removeNode(node);
return node;
}
};
148. 排序链表
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
//需要补充
class Solution {
public:
ListNode* sortList(ListNode* head) {
if(head == NULL || head->next == NULL)
return head;
ListNode* fast = head;
ListNode* slow = head;
ListNode* brk;
while(fast != NULL && fast->next != NULL){
fast = fast->next->next;
if(fast == NULL || fast->next == NULL)
brk = slow;
slow = slow->next;
}
brk->next = nullptr;
ListNode* head1 = sortList(head);
ListNode* head2 = sortList(slow);
ListNode dummy(0);
ListNode* cur = &dummy;
while(head1 != nullptr || head2 != nullptr){
if(head1 == nullptr || (head1 != nullptr && head2 != nullptr && head1->val >= head2->val)){
cur->next = head2;
head2 = head2->next;
cur = cur->next;
}else {
cur->next = head1;
head1 = head1->next;
cur = cur->next;
}
}
return dummy.next;
}
};
152. 乘积最大子数组
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
子数组 是数组的连续子序列。
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
class Solution {
public:
int maxProduct(vector<int>& nums) {
int res = nums[0], prevMin = nums[0], prevMax = nums[0];
int temp1 = 0, temp2 = 0;
for (int i = 1; i < nums.size(); i++) {
temp1 = prevMin * nums[i];
temp2 = prevMax * nums[i];
prevMin = min(min(temp1, temp2), nums[i]);
prevMax = max(max(temp1, temp2), nums[i]);
res = max(prevMax, res);
}
return res;
}
};
155. 最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。
class MinStack {
stack<int> x_stack;
stack<int> min_stack;
public:
MinStack() {
min_stack.push(INT_MAX);
}
void push(int x) {
x_stack.push(x);
min_stack.push(min(min_stack.top(), x));
}
void pop() {
x_stack.pop();
min_stack.pop();
}
int top() {
return x_stack.top();
}
int getMin() {
return min_stack.top();
}
};
/**
* Your MinStack object will be instantiated and called as such:
* MinStack* obj = new MinStack();
* obj->push(val);
* obj->pop();
* int param_3 = obj->top();
* int param_4 = obj->getMin();
*/
160. 相交链表
// 双链表解法
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode* p1 = headA;
ListNode* p2 = headB;
while(p1!=p2){
if(p1){
p1 = p1->next;
}else{
p1 =headB;
}
if(p2){
p2 = p2->next;
}else{
p2 = headA;
}
}
return p1;
}
};
169. 多数元素
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
解法二: 哈希存储,然后判断
解法一: 正负粒子的理解
class Solution {
public int majorityElement(int[] nums) {
// 我们想寻找的那个众数
int target = 0;
// 计数器(类比带电粒子例子中的带电性)
int count = 0;
for (int i = 0; i < nums.length; i++) {
if (count == 0) {
// 当计数器为 0 时,假设 nums[i] 就是众数
target = nums[i];
// 众数出现了一次
count = 1;
} else if (nums[i] == target) {
// 如果遇到的是目标众数,计数器累加
count++;
} else {
// 如果遇到的不是目标众数,计数器递减
count--;
}
}
// 回想带电粒子的例子
// 此时的 count 必然大于 0,此时的 target 必然就是目标众数
return target;
}
}
198. 打家劫舍
- dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]。
- 决定dp[i]的因素就是第i房间偷还是不偷。
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]); - dp[0] = nums[0]; dp[1] = max(nums[0], nums[1]);
- dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的,那么一定是从前到后遍历
- !
class Solution {
public:
int rob(vector<int>& nums) {
if (nums.size() == 0) return 0;
if (nums.size() == 1) return nums[0];
vector<int> dp(nums.size());
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
for (int i = 2; i < nums.size(); i++) {
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[nums.size() - 1];
}
};
200. 岛屿数量
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
class Solution {
public:
int res = 0;
int numIslands(vector<vector<char>>& grid) {
int row = grid.size();
int col = grid[0].size();
for(int i =0;i<row;i++){
for(int j =0;j<col;j++){
if(grid[i][j]=='1'){
res++;
dfs(grid,i,j);
}
}
}
return res;
}
void dfs(vector<vector<char>>& grid,int i,int j){
int row = grid.size();
int col = grid[0].size();
if(i<0||i>=row||j<0||j>=col){
return;
}
if(grid[i][j]=='0'){
return;
}
grid[i][j]='0';
dfs(grid,i-1,j);
dfs(grid,i+1,j);
dfs(grid,i,j-1);
dfs(grid,i,j+1);
}
};
206. 反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
迭代形式
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* pre = nullptr;
ListNode* cur = head;
ListNode* next = nullptr; // 可以指向nullptr,循环里面要重新指向
while(cur){
// 指针重定位
next = cur->next;
cur->next = pre;
// 更新状态
pre = cur;
cur = next;
}
return pre;
}
};
递归形式
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if (head==nullptr || head->next==nullptr) {
return head;
}
ListNode* newHead = reverseList(head->next);
head->next->next = head;
head->next = nullptr;
return newHead;
}
};
【61-80】
207. 课程表
环检测及拓扑排序算法
【拓扑排序】
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。
**请你判断是否可能完成所有课程的学习?**如果可以,返回 true ;否则,返回 false 。
首先转换为有向图!
class Solution {
public:
vector<vector<int>> g;
vector<int> vis;
vector<int> onpath;
bool isCircle = false;
public:
void build(vector<vector<int>>& a){
for(const vector<int>& item : a){
g[item[1]].push_back(item[0]);
}
}
void tranverse(vector<vector<int>>& a,int s){
if(onpath[s]) isCircle = true;
if(onpath[s] || vis[s]) return;
vis[s] = 1;
onpath[s] = 1;
for(int num : g[s]){
tranverse(a,num);
}
onpath[s] = 0;
}
bool canFinish(int n, vector<vector<int>>& a) {
onpath.resize(n);
vis.resize(n);
g.resize(n);
build(a);
for(int i = 0; i < n; i++){
tranverse(a,i);
}
return !isCircle;
}
};
208. 实现 Trie (前缀树) !!
Trie(发音类似 “try”)或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。
class Trie {
private:
vector<Trie*> children;
bool isEnd;
Trie* searchPrefix(string prefix) {
Trie* node = this;
for (char ch : prefix) {
ch -= 'a';
if (node->children[ch] == nullptr) {
return nullptr;
}
node = node->children[ch];
}
return node;
}
public:
Trie() : children(26), isEnd(false) {}
void insert(string word) {
Trie* node = this;
for (char ch : word) {
ch -= 'a';
if (node->children[ch] == nullptr) {
node->children[ch] = new Trie();
}
node = node->children[ch];
}
node->isEnd = true;
}
bool search(string word) {
Trie* node = this->searchPrefix(word);
return node != nullptr && node->isEnd;
}
bool startsWith(string prefix) {
return this->searchPrefix(prefix) != nullptr;
}
};
215. 数组中的第K个最大元素
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
// 堆的创建 大小排序和正常的相反 此处为小顶堆
priority_queue<int,vector<int>,greater<int>> pq;;
for(int i = 0; i < nums.size(); i++){
if(pq.size()<k){
pq.push(nums[i]);
}else{
if(pq.top()<nums[i]){
pq.pop();
pq.push(nums[i]);
}
}
}
return pq.top();
}
};
221. 最大正方形
在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内,找到只包含 ‘1’ 的最大正方形,并返回其面积。
解法:动态规划
这道题不难,关键是你要观察出一个全是 1 的正方形有什么特点,如何根据小的正方形推导出大的正方形(状态转移方程)。
状态转移方程
if (matrix[i][j] == 1)
// 类似「水桶效应」,最大边长取决于边长最短的那个正方形
dp[i][j] = min(dp[i-1][j], dp[i-1][j-1], dp[i][j-1]) + 1;
else
dp[i][j] = 0;
代码
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
// 定义:以 matrix[i][j] 为右下角元素的全为 1
// 正方形矩阵的最大边长为 dp[i][j]
vector<vector<int>> dp(m,vector<int>(n));
// base case,第一行和第一列的正方形边长
for (int i = 0; i < m; i++) {
dp[i][0] = matrix[i][0] - '0';
}
for (int j = 0; j < n; j++) {
dp[0][j] = matrix[0][j] - '0';
}
// 进行状态转移
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (matrix[i][j] == '0') {
// 值为 0 不可能是正方形的右下角
continue;
}
dp[i][j] = min(min(
dp[i - 1][j],
dp[i][j - 1]),
dp[i - 1][j - 1]
) + 1;
}
}
int len = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
len = max(len, dp[i][j]);
}
}
return len * len;
}
};
226. 翻转二叉树
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (root == NULL) return root;
swap(root->left, root->right); // 中
invertTree(root->left); // 左
invertTree(root->right); // 右
return root;
}
};
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
swap(node->left, node->right); // 节点处理
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return root;
}
};
234. 回文链表
给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。
把原始链表反转存入一条新的链表,然后比较这两条链表是否相同。
// 将其复制到数组中使用双指针法
class Solution {
public:
bool isPalindrome(ListNode* head) {
vector<int> vals;
while (head != nullptr) {
vals.emplace_back(head->val);
head = head->next;
}
for (int i = 0, j = (int)vals.size() - 1; i < j; ++i, --j) {
if (vals[i] != vals[j]) {
return false;
}
}
return true;
}
};
更聪明一些的办法是借助双指针算法:
1、先通过 双指针技巧 中的快慢指针来找到链表的中点:
2、如果 fast 指针没有指向 null,说明链表长度为奇数,slow 还要再前进一步:
3、从 slow 开始反转后面的链表,现在就可以开始比较回文串了:
class Solution {
public boolean isPalindrome(ListNode head) {
ListNode slow, fast;
slow = fast = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
}
if (fast != null)
slow = slow.next;
ListNode left = head;
ListNode right = reverse(slow);
while (right != null) {
if (left.val != right.val)
return false;
left = left.next;
right = right.next;
}
return true;
}
ListNode reverse(ListNode head) {
ListNode pre = null, cur = head;
while (cur != null) {
ListNode next = cur.next;
cur.next = pre;
pre = cur;
cur = next;
}
return pre;
}
}
// 详细解析参见:
// https://labuladong.github.io/article/?qno=234
236. 二叉树的最近公共祖先
GIT原理之最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

先给出递归函数的定义:给该函数输入三个参数 root,p,q,它会返回一个节点:
情况 1,如果 p 和 q 都在以 root 为根的树中,函数返回的即使 p 和 q 的最近公共祖先节点。
情况 2,那如果 p 和 q 都不在以 root 为根的树中怎么办呢?函数理所当然地返回 null 呗。
情况 3,那如果 p 和 q 只有一个存在于 root 为根的树中呢?函数就会返回那个节点。
- 根据这个定义,分情况讨论:
情况 1,如果 p 和 q 都在以 root 为根的树中,那么 left 和 right 一定分别是 p 和 q(从 base case 看出来的)。
情况 2,如果 p 和 q 都不在以 root 为根的树中,直接返回 null。
情况 3,如果 p 和 q 只有一个存在于 root 为根的树中,函数返回该节点。
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == q || root == p || root == NULL) return root;
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if (left != NULL && right != NULL) return root;
if (left == NULL && right != NULL) return right;
else if (left != NULL && right == NULL) return left;
else { // (left == NULL && right == NULL)
return NULL;
}
}
};
238. 除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
class Solution {
public:
vector<int> productExceptSelf(vector<int>& a) {
int n = a.size();
vector<int> b(n,1);
int s = 1;
//先乘左边,从左到右
for(int i = 0; i<n;i++){
//每多一位由数组B左边的元素多乘一个前面A的元素
b[i] *=s;
s*=a[i];
}
s = 1;
//再乘右边,从右到左
for(int i = n-1;~i;i--){
//temp为右边的累乘
b[i]*=s;
s*=a[i];
}
return b;
}
};
239. 滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
class Solution {
public:
class myque{
public:
deque<int> que;
void pop(int val){
if(!que.empty()&&que.front()==val){
que.pop_front();
}
}
void push(int val){
while(!que.empty()&&que.back()<val){
que.pop_back();
}
que.push_back(val);
}
int front(){
return que.front();
}
};
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
myque que;
vector<int> res;
for(int i =0;i<k;i++){
que.push(nums[i]);
}
res.push_back(que.front());
for (int i = k; i < nums.size(); i++) {
que.pop(nums[i - k]); // 滑动窗口移除最前面元素
que.push(nums[i]); // 滑动窗口前加入最后面的元素
res.push_back(que.front()); // 记录对应的最大值
}
return res;
}
};
240. 搜索二维矩阵 II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int m = matrix.size(), n = matrix[0].size();
// 初始化在右上角
int i = 0, j = n - 1;
while (i < m && j >= 0) {
if (matrix[i][j] == target) {
return true;
}
if (matrix[i][j] < target) {
// 需要大一点,往下移动
i++;
} else {
// 需要小一点,往左移动
j--;
}
}
// while 循环中没有找到,则 target 不存在
return false;
}
};
253. 会议室 II
279. 完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
完全平方数就是物品(可以无限件使用),凑个正整数n就是背包,问凑满这个背包最少有多少物品?
-
dp[j]:和为j的完全平方数的最少数量为dp[j]
-
dp[j] 可以由dp[j - i * i]推出, dp[j - i * i] + 1 便可以凑成dp[j]。
此时我们要选择最小的dp[j],所以递推公式:dp[j] = min(dp[j - i * i] + 1, dp[j]); -
dp[0]表示 和为0的完全平方数的最小数量,那么dp[0]一定是0。
非0下标的dp[j]一定要初始为最大值,这样dp[j]在递推的时候才不会被初始值覆盖。 -
都是可以
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n + 1, INT_MAX);
dp[0] = 0;
for (int i = 0; i <= n; i++) { // 遍历背包
for (int j = 1; j * j <= i; j++) { // 遍历物品
dp[i] = min(dp[i - j * j] + 1, dp[i]);
}
}
return dp[n];
}
};
283. 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
进阶:你能尽量减少完成的操作次数吗?
双指针技巧
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int n = nums.size(), left = 0, right = 0;
while (right < n) {
if (nums[right]!=0) {
swap(nums[left], nums[right]);
left++;
right++;
}else{
right++;
}
}
}
};
287. 寻找重复数
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
class Solution {
public:
int findDuplicate(vector<int>& nums) {
unordered_map<int,int> umap;
for(auto& num : nums){
if(umap.find(num) == umap.end()){
umap[num]++;
}else
return num;
}
return -1;
}
};
297. 二叉树的序列化与反序列化
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
class Solution {
private:
string SerializeCore(TreeNode* root) {
if(root == nullptr) {
return "#!";
}
string str;
str +=to_string(root->val) + '!';
str +=SerializeCore(root->left);
str +=SerializeCore(root->right);
return str;
}
TreeNode* DeserializeCore(char*& str) {
if(*str == '#'){
str++;
return nullptr;
}
int num = 0;
while( *str != '!'){
num = num*10 + (*str)-'0';
str++;
}
TreeNode *node = new TreeNode(num);
node->left = DeserializeCore(++str);
node->right = DeserializeCore(++str);
return node;
}
public:
char* Serialize(TreeNode* root) {
string str = SerializeCore(root);
char *chs = new char[str.size()];
for(int i = 0;i<str.size();++i){
chs[i] = str[i];
}
return chs;
}
TreeNode* Deserialize(char* str) {
return DeserializeCore(str);
}
};
300. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
输入:nums = [0,1,0,3,2,3]
输出:4
- dp[i]表示i之前包括i的以nums[i]结尾最长上升子序列的长度
- if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
注意这里不是要dp[i] 与 dp[j] + 1进行比较,而是我们要取dp[j] + 1的最大值。 - 每一个i,对应的dp[i](即最长上升子序列)起始大小至少都是1.
- j其实就是0到i-1,遍历i的循环在外层,遍历j则在内层
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
if (nums.size() == 0) return 0;
int result = 1;
vector<int> dp(nums.size() ,1);
for (int i = 0; i < nums.size() - 1; i++) {
if (nums[i + 1] > nums[i]) { // 连续记录
dp[i + 1] = dp[i] + 1;
}
if (dp[i + 1] > result) result = dp[i + 1];
}
return result;
}
};
301. 删除无效的括号
hot100的解法
给你一个由若干括号和字母组成的字符串 s ,删除最小数量的无效括号,使得输入的字符串有效。
返回所有可能的结果。答案可以按 任意顺序 返回。
输入:s = “()())()”
输出:[“(())()”,“()()()”]
输入:s = “(a)())()”
输出:[“(a())()”,“(a)()()”]
class Solution {
public:
bool isValid(string str) {
int count = 0;
for (char c : str) {
if (c == '(') {
count++;
} else if (c == ')') {
count--;
if (count < 0) {
return false;
}
}
}
return count == 0;
}
vector<string> removeInvalidParentheses(string s) {
vector<string> ans;
unordered_set<string> currSet;
currSet.insert(s);
while (true) {
for (auto & str : currSet) {
if (isValid(str))
ans.emplace_back(str);
}
if (ans.size() > 0) {
return ans;
}
unordered_set<string> nextSet;
for (auto & str : currSet) {
for (int i = 0; i < str.size(); i++) {
if (i > 0 && str[i] == str[i - 1]) {
continue;
}
if (str[i] == '(' || str[i] == ')') {
nextSet.insert(str.substr(0, i) + str.substr(i + 1, str.size()));
}
}
}
currSet = nextSet;
}
}
};
309. 最佳买卖股票时机含冷冻期
给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
输入: prices = [1,2,3,0,2]
输出: 3
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
if (n == 0) return 0;
vector<vector<int>> dp(n, vector<int>(4, 0));
dp[0][0] -= prices[0]; // 持股票
for (int i = 1; i < n; i++) {
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
}
return max(dp[n - 1][3],max(dp[n - 1][1], dp[n - 1][2]));
}
};
312. 戳气球
有 n 个气球,编号为0 到 n - 1,每个气球上都标有一个数字,这些数字存在数组 nums 中。
现在要求你戳破所有的气球。戳破第 i 个气球,你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。 这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界,那么就当它是一个数字为 1 的气球。
求所能获得硬币的最大数量。
输入:nums = [3,1,5,8]
输出:167
解释:
nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins = 315 + 358 + 138 + 181 = 167
动态规划
子问题必须独立。所以对于这个戳气球问题,如果想用动态规划,必须巧妙地定义dp数组的含义,避免子问题产生相关性,才能推出合理的状态转移方程。
dp[i][j] = x表示,戳破气球i和气球j之间(开区间,不包括i和j)的所有气球,可以获得的最高分数为x。
那么根据这个定义,题目要求的结果就是dp[0][n+1]的值,而 base case 就是dp[i][j] = 0,其中0 <= i <= n+1, j <= i+1,因为这种情况下,开区间(i, j)中间根本没有气球可以戳。
「反向思考」,想一想气球i和气球j之间最后一个被戳破的气球可能是哪一个?
根据刚才对dp数组的定义,如果最后一个戳破气球k,dp[i][j]的值应该为
dp[i][j] = dp[i][k] + dp[k][j] + points[i]*points[k]*points[j]
class Solution {
public:
int maxCoins(vector<int>& nums) {
int n = nums.size();
// 添加两侧的虚拟气球
vector<int> points(n+2);
points[0] = points[n + 1] = 1;
for (int i = 1; i <= n; i++) {
points[i] = nums[i - 1];
}
// base case 已经都被初始化为 0
vector<vector<int>> dp(n+2,vector<int>(n+2));
// 开始状态转移
// i 应该从下往上
for (int i = n; i >= 0; i--) {
// j 应该从左往右
for (int j = i + 1; j < n + 2; j++) {
// 最后戳破的气球是哪个?
for (int k = i + 1; k < j; k++) {
// 择优做选择
dp[i][j] = max(
dp[i][j],
dp[i][k] + dp[k][j] + points[i]*points[j]*points[k]
);
}
}
}
return dp[0][n + 1];
}
};
不同顺序 转换成求全排列的问题,
int res = Integer.MIN_VALUE;
/* 输入一组气球,返回戳破它们获得的最大分数 */
int maxCoins(int[] nums) {
backtrack(nums, 0);
return res;
}
/* 回溯算法的伪码解法 */
void backtrack(int[] nums, int socre) {
if (nums 为空) {
res = max(res, score);
return;
}
for (int i = 0; i < nums.length; i++) {
int point = nums[i-1] * nums[i] * nums[i+1];
int temp = nums[i];
// 做选择
在 nums 中删除元素 nums[i]
// 递归回溯
backtrack(nums, score + point);
// 撤销选择
将 temp 还原到 nums[i]
}
}
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
- dp[j]:凑成总金额j的货币组合数为dp[j]
- dp[j] += dp[j - coins[i]];
dp[j] (考虑coins[i]的组合总和) 就是所有的dp[j - coins[i]](不考虑coins[i])相加。 - 首先dp[0]一定要为1,dp[0] = 1是 递归公式的基础。
下标非0的dp[j]初始化为0,这样累计加dp[j - coins[i]]的时候才不会影响真正的dp[j] - 外层for循环遍历物品(钱币),内层for遍历背包(金钱总额)
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount + 1, INT_MAX);
dp[0] = 0;
for (int i = 0; i < coins.size(); i++) { // 遍历物品
for (int j = coins[i]; j <= amount; j++) { // 遍历背包
if (dp[j - coins[i]] != INT_MAX) { // 如果dp[j - coins[i]]是初始值则跳过
dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
}
}
}
if (dp[amount] == INT_MAX) return -1;
return dp[amount];
}
};
【81-100】
337. 打家劫舍 III
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。
本题一定是要后序遍历,因为通过递归函数的返回值来做下一步计算。
// 下标0:不偷,下标1:偷
// 偷cur
int val1 = cur->val + left[0] + right[0];
// 不偷cur
int val2 = max(left[0], left[1]) + max(right[0], right[1]);
class Solution {
public:
int rob(TreeNode* root) {
vector<int> result = robTree(root);
return max(result[0], result[1]);
}
// 长度为2的数组,0:不偷,1:偷
vector<int> robTree(TreeNode* cur) {
if (cur == NULL) return vector<int>{0, 0};
vector<int> left = robTree(cur->left);
vector<int> right = robTree(cur->right);
// 偷cur
int val1 = cur->val + left[0] + right[0];
// 不偷cur
int val2 = max(left[0], left[1]) + max(right[0], right[1]);
return {val2, val1};
}
};
338. 比特位计数
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
class Solution {
public:
vector<int> countBits(int n) {
vector<int> res;
for(int i =0;i<=n;i++){
int n = countBit(i);
res.push_back(n);
}
return res;
}
int countBit(int num){
int res = 0;
while(num>0){
num = num&(num-1);
res++;
}
return res;
}
};
347. 前 K 个高频元素
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
定义一个哈希map,遍历统计频率;
然后定义一个小顶堆,保持个数为k,添加元素的同时把小的数据pop掉,最后剩下的就是前k个高频数据了。
注意:priority_queue
Mycomparision的定义中 与 排序算法相反,lhs.second > rhs.second; 建立小根堆。
// 时间复杂度:O(nlogk)
// 空间复杂度:O(n)
class Solution {
public:
// 小顶堆
class mycomparison {
public:
bool operator()(const pair<int, int>& lhs, const pair<int, int>& rhs)
{
return lhs.second > rhs.second;
}
};
vector<int> topKFrequent(vector<int>& nums, int k) {
// 要统计元素出现频率
unordered_map<int, int> map; // map394. 字符串解码
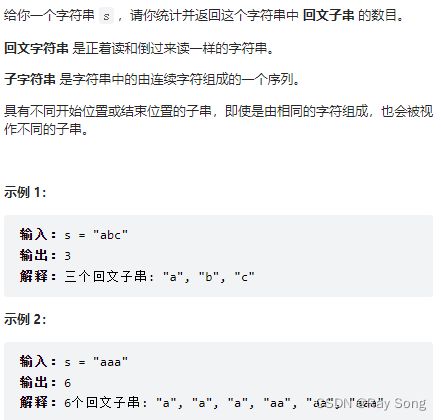
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
输入:s = “3[a]2[bc]”
输出:“aaabcbc”
class Solution {
public:
string decodeString(string s) {
int n = s.length();
stack<string> stk;
for(int i = n - 1;i>=0;){
char c = s[i];
if(c==']' || 'a'<=c && c<='z'){
stk.push(string(1,c));
i--;//i--
}else{
// '['
string block;
while(!stk.empty() && stk.top() != "]"){
block += stk.top();
stk.pop();
}
if(!stk.empty()) stk.pop();
//解析 重复次数
i--;
int val = 0,base = 1;
while(i>=0 && isdigit(s[i])){
val = val + (s[i]-'0')*base;
base *=10;
i--;//--
}
string str;
while(val) str+=block,val--;//重复value次
stk.push(str);
}
}
string res;
while(!stk.empty()) res += stk.top(),stk.pop();
return res;
}
};
399. 除法求值 —
class Solution {
public:
vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
int nvars = 0;
unordered_map<string, int> variables;
int n = equations.size();
for (int i = 0; i < n; i++) {
if (variables.find(equations[i][0]) == variables.end()) {
variables[equations[i][0]] = nvars++;
}
if (variables.find(equations[i][1]) == variables.end()) {
variables[equations[i][1]] = nvars++;
}
}
// 对于每个点,存储其直接连接到的所有点及对应的权值
vector<vector<pair<int, double>>> edges(nvars);
for (int i = 0; i < n; i++) {
int va = variables[equations[i][0]], vb = variables[equations[i][1]];
edges[va].push_back(make_pair(vb, values[i]));
edges[vb].push_back(make_pair(va, 1.0 / values[i]));
}
vector<double> ret;
for (const auto& q: queries) {
double result = -1.0;
if (variables.find(q[0]) != variables.end() && variables.find(q[1]) != variables.end()) {
int ia = variables[q[0]], ib = variables[q[1]];
if (ia == ib) {
result = 1.0;
} else {
queue<int> points;
points.push(ia);
vector<double> ratios(nvars, -1.0);
ratios[ia] = 1.0;
while (!points.empty() && ratios[ib] < 0) {
int x = points.front();
points.pop();
for (const auto [y, val]: edges[x]) {
if (ratios[y] < 0) {
ratios[y] = ratios[x] * val;
points.push(y);
}
}
}
result = ratios[ib];
}
}
ret.push_back(result);
}
return ret;
}
};
406. 根据身高重建队列
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
两个维度,h 和 k
遇到两个维度权衡的时候,一定要先确定一个维度,再确定另一个维度。
思路
-
那么按照身高h来排序呢,身高一定是从大到小排(身高相同的话则k小的站前面),让高个子在前面。
-
按照身高排序之后,优先按身高高的people的k来插入,后序插入节点也不会影响前面已经插入的节点,最终按照k的规则完成了队列。
所以在按照身高从大到小排序后:
局部最优:优先按身高高的people的k来插入。插入操作过后的people满足队列属性
全局最优:最后都做完插入操作,整个队列满足题目队列属性
// 版本一
class Solution {
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
sort (people.begin(), people.end(),
[](const vector<int>& a, const vector<int>& b)
{
if (a[0] == b[0]) return a[1] < b[1];
return a[0] > b[0];
});
vector<vector<int>> que;
for (int i = 0; i < people.size(); i++) {
int position = people[i][1];
que.insert(que.begin() + position, people[i]);
}
return que;
}
};
class Solution {
public:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
// 大于或等于,如果
sort(people.begin(),people.end(),[](vector<int>& a,vector<int> &b){
if(a[0]!=b[0])return a[0]>b[0];
return a[1]<b[1];
});
vector<vector<int>> res;
for(int i = 0;i<people.size();i++){
res.push_back(people[i]);
int idx = res.size()-1;
while(idx>res[idx][1]){
swap(res[idx],res[idx-1]);
idx--;
}
}
return res;
}
};
416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
- dp[j]表示 背包总容量是j,最大可以凑成j的子集总和为dp[j]。
- dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
- vector dp(10001, 0);
- 物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
- 举例推导dp数组
dp[j]的数值一定是小于等于j的。
如果dp[j] == j 说明,集合中的子集总和正好可以凑成总和j,理解这一点很重要。
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
vector<int> dp(20001,0);
for(int& num:nums){
sum+=num;
}
if(sum%2==1){
return false;
}
int target = sum/2;
for(int i = 0;i<nums.size();i++){//物品
for(int j = target;j>=nums[i];j--){//背包
dp[j] = max(dp[j],dp[j-nums[i]]+nums[i]);
}
}
if(dp[target]==target){
return true;
}
return false;
}
};
437. 路径总和 II
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
class Solution {
public:
int rootSum(TreeNode* root, long long targetSum) {
if (!root) {
return 0;
}
long long ret = 0;
if (root->val == targetSum) {
ret++;
}
ret += rootSum(root->left, targetSum - root->val);
ret += rootSum(root->right, targetSum - root->val);
return ret;
}
int pathSum(TreeNode* root, long long targetSum) {
if (!root) {
return 0;
}
long long ret = rootSum(root, targetSum);
ret += pathSum(root->left, targetSum);
ret += pathSum(root->right, targetSum);
return ret;
}
};
438. 找到字符串中所有字母异位词
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
输入: s = “cbaebabacd”, p = “abc”
输出: [0,6]
解释:
起始索引等于 0 的子串是 “cba”, 它是 “abc” 的异位词。
起始索引等于 6 的子串是 “bac”, 它是 “abc” 的异位词。
class Solution {
public:
vector<int> findAnagrams(string s, string t) {
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
int left = 0, right = 0;
int valid = 0;
vector<int> res; // 记录结果
while (right < s.size()) {
char c = s[right];
right++;
// 进行窗口内数据的一系列更新
if (need.count(c)) {
window[c]++;
if (window[c] == need[c])
valid++;
}
// 判断左侧窗口是否要收缩
while (right - left >= t.size()) {
// 当窗口符合条件时,把起始索引加入 res
if (valid == need.size())
res.push_back(left);
char d = s[left];
left++;
// 进行窗口内数据的一系列更新
if (need.count(d)) {
if (window[d] == need[d])
valid--;
window[d]--;
}
}
}
return res;
}
};
448. 找到所有数组中消失的数字
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
进阶:你能在不使用额外空间且时间复杂度为 O(n) 的情况下解决这个问题吗? 你可以假定返回的数组不算在额外空间内。
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
int n = nums.size();
for (auto& num : nums) {
int x = (num - 1) % n;
nums[x] += n;
}
vector<int> ret;
for (int i = 0; i < n; i++) {
if (nums[i] <= n) {
ret.push_back(i + 1);
}
}
return ret;
}
};
461. 汉明距离
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数 x 和 y,计算并返回它们之间的汉明距离。
// 最佳方法
class Solution {
public:
int hammingDistance(int x, int y) {
int s = x ^ y, ret = 0;
while (s) {
s &= s - 1;
ret++;
}
return ret;
}
};
// 移位置运算
class Solution {
public:
int hammingDistance(int x, int y) {
int s = x ^ y, ret = 0;
while (s) {
ret += s & 1;
s >>= 1;
}
return ret;
}
};
494. 目标和
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

回溯解法+剪枝
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
if (sum == target) {
result.push_back(path);
}
// 如果 sum + candidates[i] > target 就终止遍历
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
sum += candidates[i];
path.push_back(candidates[i]);
backtracking(candidates, target, sum, i + 1);
sum -= candidates[i];
path.pop_back();
}
}
public:
int findTargetSumWays(vector<int>& nums, int S) {
int sum = 0;
for (int i = 0; i < nums.size(); i++) sum += nums[i];
if (S > sum) return 0; // 此时没有方案
if ((S + sum) % 2) return 0; // 此时没有方案,两个int相加的时候要各位小心数值溢出的问题
int bagSize = (S + sum) / 2; // 转变为组合总和问题,bagsize就是要求的和
// 以下为回溯法代码
result.clear();
path.clear();
sort(nums.begin(), nums.end()); // 需要排序
backtracking(nums, bagSize, 0, 0);
return result.size();
}
};
解法二:
01背包解法:
既然为target,那么就一定有 left组合 - right组合 = target。
left + right等于sum,而sum是固定的。
公式来了, left - (sum - left) = target -> left = (target + sum)/2 。
target是固定的,sum是固定的,left就可以求出来。
此时问题就是在集合nums中找出和为left的组合。
- dp[j] 表示:填满j(包括j)这么大容积的包,有dp[j]种方法。
- dp[j] += dp[j - nums[i]]
不考虑nums[i]的情况下,填满容量为j - nums[i]的背包,有dp[j - nums[i]]种方法。
那么只要搞到nums[i]的话,凑成dp[j]就有dp[j - nums[i]] 种方法。
-
dp[0] = 1,理论上也很好解释,装满容量为0的背包,有1种方法,就是装0件物品。
dp[j]其他下标对应的数值应该初始化为0,从递归公式也可以看出,dp[j]要保证是0的初始值,才能正确的由dp[j - nums[i]]推导出来。 -
nums放在外循环,target在内循环,且内循环倒序。
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int S) {
int sum = 0;
for (int i = 0; i < nums.size(); i++) sum += nums[i];
if (abs(S) > sum) return 0; // 此时没有方案
if ((S + sum) % 2 == 1) return 0; // 此时没有方案
int bagSize = (S + sum) / 2;
vector<int> dp(bagSize + 1, 0);
dp[0] = 1;
for (int i = 0; i < nums.size(); i++) {
for (int j = bagSize; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[bagSize];
}
};
538. 把二叉搜索树转换为累加树
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),
使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。
类似于二叉搜索树的第k个大的树的做法
将中序遍历的步骤,倒转一下
中序遍历 从小到大
中序遍历先访问右边 从大到小
一边统计序列,一边统计前缀和
class Solution {
public:
int sum = 0;
TreeNode* convertBST(TreeNode* root) {
if (!root) return root;
convertBST(root->right);
sum += root->val;
root->val = sum;
convertBST(root->left);
return root;
}
};
543. 二叉树的直径
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
class Solution {
public:
int ans;
int depth(TreeNode* rt){
if (rt == NULL) {
return 0; // 访问到空节点了,返回0
}
int L = depth(rt->left); // 左儿子为根的子树的深度
int R = depth(rt->right); // 右儿子为根的子树的深度
ans = max(ans, L + R + 1); // 计算d_node即L+R+1 并更新ans
return max(L, R) + 1; // 返回该节点为根的子树的深度
}
int diameterOfBinaryTree(TreeNode* root) {
ans = 0;
depth(root);
return ans - 1; // 求路径,不是求节点个数,要减去1
}
};
560. 和为 K 的子数组
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。
解法一:前缀和 + 枚举子区间 n^2的时间复杂度,过不了
解法二:前缀和+ 哈希表 倒序遍历,只枚举左端点,将右端点加入哈希表
class Solution {
public:
int subarraySum(vector<int>& nums, int k) {
int n = nums.size();
vector<int> presum(nums.size()+1,0);
for(int i = 1; i <= n; i++){
presum[i] = presum[i-1] + nums[i-1];
}
int ret = 0;
unordered_map<int,int> data;
for(int l = n; l ; l--){
data[presum[l]]++;
int target = presum[l-1] + k;
if(data.count(target))
ret += data[target];
}
return ret;
}
};
581. 最短无序连续子数组
给你一个整数数组 nums ,你需要找出一个 连续子数组 ,如果对这个子数组进行升序排序,那么整个数组都会变为升序排序。
请你找出符合题意的 最短 子数组,并输出它的长度。
输入:nums = [2,6,4,8,10,9,15]
输出:5
解释:你只需要对 [6, 4, 8, 10, 9] 进行升序排序,那么整个表都会变为升序排序。
class Solution {
public:
int findUnsortedSubarray(vector<int>& nums) {
if (is_sorted(nums.begin(), nums.end())) {
return 0;
}
vector<int> numsSorted(nums);
sort(numsSorted.begin(), numsSorted.end());
int left = 0;
while (nums[left] == numsSorted[left]) {
left++;
}
int right = nums.size() - 1;
while (nums[right] == numsSorted[right]) {
right--;
}
return right - left + 1;
}
};
617. 合并二叉树
//-----------------
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if (t1 == NULL) return t2;
if (t2 == NULL) return t1;
// 重新定义新的节点,不修改原有两个树的结构
TreeNode* root = new TreeNode(0);
root->val = t1->val + t2->val;
root->left = mergeTrees(t1->left, t2->left);
root->right = mergeTrees(t1->right, t2->right);
return root;
}
};
621. 任务调度器
给你一个用字符数组 tasks 表示的 CPU 需要执行的任务列表。其中每个字母表示一种不同种类的任务。任务可以以任意顺序执行,并且每个任务都可以在 1 个单位时间内执行完。在任何一个单位时间,CPU 可以完成一个任务,或者处于待命状态。
然而,两个 相同种类 的任务之间必须有长度为整数 n 的冷却时间,因此至少有连续 n 个单位时间内 CPU 在执行不同的任务,或者在待命状态。
你需要计算完成所有任务所需要的 最短时间 。
贪心策略
先把最大的任务排列求出来,求最大任务的个数
然后ret = (max-1 )*(n-1)
在判断最大的任务数有几个,ret++ 几次
最后max(ret,task.size())
class Solution {
public:
int leastInterval(vector<char>& tasks, int n) {
vector<int> temp(26,0);
for(char c : tasks)
temp[c-'A']++;
int maxval = 0;
for(int num:temp)
maxval = max(num,maxval);
int ret = (maxval - 1)*(n+1);
for(int num : temp)
if(num == maxval)
ret++;
ret = ret > tasks.size()? ret: tasks.size();
return ret;
}
};
/*
1. 任务只有26
2. 数量最多的任务,决定最短的执行时间
A 最多
A.. A.. A.. A
贪心策略
按时间思考:枚举时间
*/
class Solution {
public:
int leastInterval(vector<char>& tasks, int n) {
using pii = pair<int,int>;
// 就绪队列: 大顶堆
priority_queue<pii> pq2;
// 冷冻队列: 小顶堆
priority_queue<pii,vector<pii>,greater<pii>> pq1;
vector<int> cnt(26);//每种任务剩余的数量
vector<int> last(26,INT_MIN); //每种任务执行的时间
for(char c:tasks) cnt[c-'A']++;
for(int i = 0; i < 26; i++) if(cnt[i]) pq2.push({cnt[i],i});//添加到就绪队列
int time = 0;
while(!pq1.empty() || !pq2.empty()){
//吧冷冻队列的任务+ 到就绪队列
while(!pq1.empty() && pq1.top().first+n<time){
auto item = pq1.top();
pq1.pop();
pq2.push({cnt[item.second],item.second});
}
// 此时冷对队列中的任务都不是就绪,只能从就绪队列中选任务
if(!pq2.empty()){
auto item = pq2.top();
pq2.pop();
cnt[item.second]--;
if(cnt[item.second]){
//任务刚刚执行完,放入冷冻队列
pq1.push({time,item.second});
}
}
time++;
}
return time;
}
};
647. 回文子串
解法一:双指针法
一个元素可以作为中心点,两个元素也可以作为中心点。
class Solution {
public:
int countSubstrings(string s) {
int result = 0;
for (int i = 0; i < s.size(); i++) {
result += extend(s, i, i, s.size()); // 以i为中心
result += extend(s, i, i + 1, s.size()); // 以i和i+1为中心
}
return result;
}
int extend(const string& s, int i, int j, int n) {
int res = 0;
while (i >= 0 && j < n && s[i] == s[j]) {
i--;
j++;
res++;
}
return res;
}
};
解法二:动态规划 –
-
布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
当s[i]与s[j]不相等,那没啥好说的了,dp[i][j]一定是false。
当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况:
情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
情况二:下标i 与 j相差为1,例如aa,也是回文子串
情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
- 所以dp[i][j]初始化为false。
4 情况三是根据dp[i + 1][j - 1]是否为true,在对dp[i][j]进行赋值true的。
从下到上,从左到右遍历,这样保证dp[i + 1][j - 1]都是经过计算的。
class Solution {
public:
int countSubstrings(string s) {
vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
int result = 0;
for (int i = s.size() - 1; i >= 0; i--) { // 注意遍历顺序
for (int j = i; j < s.size(); j++) {
if (s[i] == s[j]) {
if (j - i <= 1) { // 情况一 和 情况二
result++;
dp[i][j] = true;
} else if (dp[i + 1][j - 1]) { // 情况三
result++;
dp[i][j] = true;
}
}
}
}
return result;
}
};
739. 每日温度
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
单调栈里只需要存放元素的下标i就可以了,如果需要使用对应的元素,直接T[i]就可以获取。
情况一:当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
情况二:当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
情况三:当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
// 版本一
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& T) {
// 递增栈
stack<int> st;
vector<int> result(T.size(), 0);
st.push(0);
for (int i = 1; i < T.size(); i++) {
if (T[i] < T[st.top()]) { // 情况一
st.push(i);
} else if (T[i] == T[st.top()]) { // 情况二
st.push(i);
} else {
while (!st.empty() && T[i] > T[st.top()]) { // 情况三
result[st.top()] = i - st.top();
st.pop();
}
st.push(i);
}
}
return result;
}
};