【HDU】2865 Birthday Toy

题意：n个小圆组成的正n边形，中间有一个大圆。有木棍相连的两个圆不能有相同的颜色，旋转后相同视为相同的方案，求着色方案数。

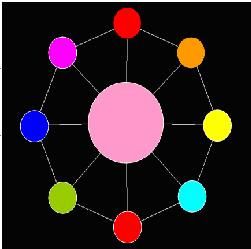
设有n个小圆，k种颜色(3<=N<=10^9, 4<=K<=10^9)。

首先，很容易想到从k种选一种给大圆，然后用k-1种颜色对小圆着色。

若不存在相邻圆颜色不同这个限制，则直接Burnside定理。

若存在限制，但是颜色种数很少，可以构造矩阵然后快速幂，得到一个置换使着色不变的着色方案数。

现在颜色种数很多，但是颜色限制较简单，可以考虑公式之类的。

考虑将n个圆的环，等分成t部分，每部分有m个圆。F表示m个圆满足限制的着色方案数。

若m=1，则F=0

若m=2，则F=k*(k-1)

若m=3，则F=k*(k-1)*(k-2)

若m=4，则F=k*(k-1)*[(k-1)+(k-2)*(k-2)]

……

观察到F[n]=F[n-1]*(k-2)+F[n-2]*(k-1)。

那么就可以对该递推式构造矩阵快速幂得到每种分法的方案数。

剩下的同【POJ】2888 Magic Bracelet。

  1 #include<cstdio>

  2 #include<cstring>

  3 #include<vector>

  4 #define P 1000000007

  5 #define MAXM 2

  6 #define MAXN 32000

  7 typedef long long LL;

  8 using namespace std;

  9 bool p[MAXN];

 10 vector<int> factor;

 11 vector<int> prime;

 12 struct Matrix {

 13     LL mat[MAXM][MAXM];

 14     void Zero() {

 15         memset(mat, 0, sizeof(mat));

 16     }

 17     void Unit() {

 18         Zero();

 19         mat[0][0] = mat[1][1] = 1;

 20     }

 21     void Build(int k) {

 22         Zero();

 23         mat[0][1] = 1;

 24         mat[0][0] = k - 2;

 25         mat[1][0] = k - 1;

 26     }

 27 };

 28 Matrix operator *(Matrix &a, Matrix &b) {

 29     int i, j, k;

 30     Matrix tmp;

 31     tmp.Zero();

 32     for (i = 0; i < MAXM; i++) {

 33         for (j = 0; j < MAXM; j++) {

 34             for (k = 0; k < MAXM; k++)

 35                 tmp.mat[i][j] += a.mat[i][k] * b.mat[k][j];

 36             tmp.mat[i][j] %= P;

 37         }

 38     }

 39     return tmp;

 40 }

 41 Matrix operator ^(Matrix a, int k) {

 42     Matrix tmp;

 43     for (tmp.Unit(); k; k >>= 1) {

 44         if (k & 1)

 45             tmp = tmp * a;

 46         a = a * a;

 47     }

 48     return tmp;

 49 }

 50 void Factor(int n) {

 51     int i;

 52     factor.clear();

 53     for (i = 1; i * i < n; i++) {

 54         if (n % i == 0) {

 55             factor.push_back(i);

 56             factor.push_back(n / i);

 57         }

 58     }

 59     if (i * i == n)

 60         factor.push_back(i);

 61 }

 62 LL ExtGcd(LL a, LL b, LL &x, LL &y) {

 63     LL t, d;

 64     if (b == 0) {

 65         x = 1;

 66         y = 0;

 67         return a;

 68     }

 69     d = ExtGcd(b, a % b, x, y);

 70     t = x;

 71     x = y;

 72     y = t - a / b * y;

 73     return d;

 74 }

 75 LL InvMod(LL a, LL n) {

 76     LL x, y;

 77     ExtGcd(a, n, x, y);

 78     return (x % n + n) % n;

 79 }

 80 int Count(int x) {

 81     int res, i;

 82     res = x;

 83     for (i = 0; prime[i] * prime[i] <= x; i++) {

 84         if (x % prime[i] == 0) {

 85             res -= res / prime[i];

 86             while (x % prime[i] == 0)

 87                 x /= prime[i];

 88         }

 89     }

 90     if (x > 1)

 91         res -= res / x;

 92     return res;

 93 }

 94 LL F(int n, int k) {

 95     LL res;

 96     if (n == 1)

 97         res = 0;

 98     else if (n == 2)

 99         res = (LL) k * (k - 1);

100     else if (n == 3)

101         res = (LL) k * (k - 1) % P * (k - 2);

102     else {

103         Matrix g;

104         g.Build(k);

105         g = g ^ (n - 3);

106         res = g.mat[0][0] * k % P * (k - 1) % P * (k - 2);

107         res += g.mat[1][0] * k % P * (k - 1);

108     }

109     return res % P;

110 }

111 LL Burnside(int n, int k) {

112     LL ans;

113     int i;

114     Factor(n);

115     for (i = ans = 0; i < (int) factor.size(); i++) {

116         ans += F(factor[i], k) * Count(n / factor[i]) % P;

117         if (ans >= P)

118             ans -= P;

119     }

120     return ans * InvMod(n, P) % P;

121 }

122 void Init() {

123     int i, j;

124     memset(p, true, sizeof(p));

125     for (i = 2; i < 180; i++) {

126         if (p[i]) {

127             for (j = i * i; j < MAXN; j += i)

128                 p[j] = false;

129         }

130     }

131     prime.clear();

132     for (i = 2; i < MAXN; i++) {

133         if (p[i])

134             prime.push_back(i);

135     }

136 }

137 int main() {

138     int n, k;

139     Init();

140     while (~scanf("%d%d", &n, &k))

141         printf("%I64d\n", Burnside(n, k - 1) * k % P);

142     return 0;

143 }