【unity shader】水体渲染基础-通过顶点偏移实现波浪

1.关于顶点波形：

为了表示宽广水域中的水体变化，往往需要进行水平面的整体运动变化。即对平面的顶点进行位移，以实现波浪的起伏效果。现在对于波浪的构成，如快速傅里叶变换和波浪的统计学理论，在游戏中的应用也相对完善。今天主要是做一个基础的波浪实现：正弦波形。

1.1. 基础正弦波形

我们拖出一块平面，修改其顶点着色器，片元着色器中我们直接返回一个海面颜色。

v2f o;
float3 p;
p = v.vertex;
p.y = sin(p.x);
//注意这里肯定不能在视口变换完后再求正弦，原因不用多说了吧？
o.vertex = UnityObjectToClipPos(p);

得到基础波形。

1.2. 幅度参数

增加幅度参数_Amplitude，主要进行波峰控制。

p.y = _Amplitude * sin(p.x);

1.3. 波长参数

波长参数_Wavelength，主要影响的是正弦函数的周期。即函数需要花费更长的时间完成一次周期性的变化，表现上的意义就是水波的宽度。
注意默认下正弦函数sin（x）的周期是2π，为了更直观地进行控制，我们要增加一个k参数作为最终的控制向量。通过2π/_Wavelength来求解k，实现_Wavelength越大，最终表现上的水波宽度增大。

float k = 2 * UNITY_PI / _Wavelength;
p.y = _Amplitude * sin(k * p.x);

注意看这里明显出现了尖锐抖动的问题，说明平面本身的顶点数显然不够支撑太细致的表现了。我们在下一步重做一下两个顶点数更多的平面来对比一下。

1.4. 波浪速度参数

_Wavespeed，这个不太需要多说明了

p.y = _Amplitude * sin(k * (p.x + _Wavespeed * _Time.y));

这里第一个是unity自带的平面，左右两个是自己做的2020，3030的平面，可以看到其在波长较小的情况，由于顶点不够下会出现硬边缘的问题。

小提示：关于blender的模型导出到unity
默认配置下，尺寸差异为五倍，且在保持

1.5. 求解法向量

目前的问题是，即便是有了波形，这个平面看起来也只是一层皮，所以需要进行法向量以便于在片元着色器里面做光照计算。
由于我们这里对顶点进行了调整，所以平面原本的法线信息肯定也不能用了，我们必须自己去求解。
首先我们要求解他的切线方向，就是求导数。
所幸的是，目前我们的向量只在x，y方向上有变化，即z方向上的导数为0。导数T = （ x’, y’ , 0 ）。
由于目前发生变化的是x，所以最终导数都是对于x进行求导， T = （ 1, k * _Amplitude * cos( k * x), 0）。
对于副切线的方向，我们很好确定，就是沿z方向的单位向量(0, 0, 1)。
最后我们通过叉乘方式获得法向量。

//in vertex shader
float3 tangent = normalize(float3(1, k * _Amplitude * cos(f), 0));
float3 normal = cross(float3(0, 0, 1.0), tangent);
//normal直接传递使用即可

//in vertex shader
float3 LightDir = normalize(_WorldSpaceLightPos0.xyz);
fixed3 diffuse = _LightColor0 * dot(i.normal, LightDir);

我们把自定义的水面颜色作为ambient，与diffuse相加返回即可。

1.6. 关于网格精度

在波长相对较大的时候，由于水波幅度本身较大，即各顶点间的位移相对变化越小，平面网格本身的差异带来的表现影响看似区别不大。当波长较小时，网格间的精度差异就会对表现产生显著影响。
当波长为2时，1010, 2020, 3030的网格表现差异就特别明显。

所以这里我们引入一个100100的高精度平面网格，进行2020，3030, 100100的网格对比。

后续我们的案例中只使用100100的平面。

1.7. 阴影的修正

我们直接上阴影三件套给正弦波附上阴影，这里显然看出来默认的阴影计算存在一些问题：虽然法线的计算已经正确了，但是顶点的变化显然没有对shadow map产生影响，从而致使阴影显得非常平面。（这边视效变了，我只是又调了一下光照参数）
主要的原因还是，默认的shadowmapping方法不支持顶点偏移的shader，所以我们需要自己去写一个shadowcaster。

对于surface shader来说，我们有比较简易的方案，让阴影计算使用我们进行顶点变化的vertex shader。

#pragma surface surf Standard fullforwardshadows vertex:vert addshadow
//#pragma surface   

但对于unlit shader来说，并不支持直接使用#pragma来指定顶点着色器，我们需要自己去写一个阴影计算的pass。
实际上shadowcaster也有三件套：
定义在fragment 结构体定义中的V2F_SHADOW_CASTER;
放在vertex shader里面做光口变换的TRANSFER_SHADOW_CASTER_NORMALOFFSET( );
放在fragment shader中的SHADOW_CASTER_FRAGMENT(i);

Pass
{
    //原本的顶点偏移pass，记得添加阴影三件套
}

Pass
{
    Tags {"LightMode"="ShadowCaster"}

    CGPROGRAM

    #pragma vertex vert 
    #pragma fragment frag
    #pragma multi_compile_shadowcaster

    #include "UnityCG.cginc"

    float _Amplitude;
    float _Wavelength, _Wavespeed;
    //阴影映射不需要颜色纹理相关的参数

    struct v2f
    {
        V2F_SHADOW_CASTER;
    };

    v2f vert(appdata_base v)
    {
        v2f o;
        float3 p;
        float k = 2 * UNITY_PI / _Wavelength;
        p = v.vertex;
        float f = k * (p.x + _Wavespeed * _Time.y);
        p.y = _Amplitude * sin(f);
        
        v.vertex.xyz = p;
        //无需进行视口变换，只需要给原有的vertex赋值
        
        TRANSFER_SHADOW_CASTER_NORMALOFFSET(o);
        
        return o;
    }

    fixed4 frag(v2f i): SV_Target
    {
    	//若需要做深度剔除，仍需要进行单独计算处理
        SHADOW_CASTER_FRAGMENT(i);
    }

    ENDCG
}

当顶点偏移计算方法改变后，shadowcaster中的vertex计算方法也要随之进行对应调整。为了简化，后续我就不再单独对shadowcaster pass进行额外说明了。

Gerstner波：

正弦波比较简单，但是显然是有点简化过头了。所以我们需要在这个基础上，更进一步。
同样的，我们做的顶点shader实际上是对模型表面的顶点（一层皮）进行处理。在正弦波中，每个顶点都遵循正弦函数，只在y轴方向上做上下运动。在Gerstner波中，顶点在做沿y轴方向的运动同时，也做沿x轴方向的运动。

在x轴方向上，可以看到顶点的偏移由正到负再到正，这个是典型的余弦函数的特征。
所以我们新的顶点方程就是在原有的x值基础上加上余弦函数作为偏移：
vertex = （x + Acos(kx), Asin(kx), 0）
求导后，即
T = (1 - Aksin(kx), Akcos(kx), 0)

副切线依然没有变化，我们可以直接使用叉乘求解法线。

p.y = _Amplitude * sin(f);
p.x += _Amplitude * cos(f);

float3 tangent = normalize(float3(1 - k * _Amplitude * sin(f), k * _Amplitude * cos(f), 0));
float3 normal = normalize(cross(float3(0, 0, 1.0), tangent));

2.1. 重叠波的调整

虽然由此产生的波浪可能看起来不错，但情况并非总是如此。 例如，将波长和波幅都减少后，会产生奇怪的结果，看起来各个波浪间出现了相互折叠的现象。


为什么会有这样的现象？主要还是因为x值计算方法的调整，加上波幅和波长两个参数的共同作用，导致不同x的计算值结果重叠的情况。

为什么会出现这样的情况？
主要是在两个参数的影响下，x2-x1的值无法保证一定比A*( cos(kx1) - cos(kx2))的值大。
当k较大时，三角函数会被极大地压缩，在一定范围内的变化幅度将非常巨大，导致A*( cos(kx1) - cos(kx2)) 的最大值为 2A。
显然A值是一个不可控的因素，为了更好的控制这种情况，我们使用1/k来代替原有的A（波幅）参数。当k增大，导致三角函数的波动较大时，1/k会相应地减少，从而削减( cos(kx1) - cos(kx2)) 的最大值，使其最大值为 2/k。此外，我们增加一个_Steepness 参数，使用_Steepness /k替换原有的波幅参数，以更好发挥波峰处的控制作用。

float _Amplitude = _Steepness / k;
float f = k * (p.x + _Wavespeed * _Time.y);
p.y = _Amplitude * sin(f);
p.x += _Amplitude * cos(f);

可以看到在使用新参数后，波峰重叠的现象大大缓解了，在进一步缩小_Steepness 后，整个波峰都会被相应地削平。

2.2. 现实中的波速

在现实物理中，波速实际上跟波长相关，即

物理的问题我们不多聊，直接进行参数替换，以后就用不着_Wavespeed了。

float _Amplitude = _Steepness / k;
//新增c，波长相关的波速参数，原有的_Wavespeed被替换
float c = sqrt(9.8 / k);
float f = k * (p.x + c * _Time.y);
p.y = _Amplitude * sin(f);
p.x += _Amplitude * cos(f);

2.3. 自定方向波

说完了以x轴为方向的，以xz平面中任一直线方向的波公式，也呼之欲出了。即x，z会同时作用于y方向的计算结果，且在x，z方向上也会根据当前的参数值发生偏移。
对于**二维方向 （x1， z1）**来说：
首先放入三角函数中的f值要变为，

f =  k *（dot（（x1, z1），（vertex.x，vertex.z）+ c * _Time.y）

所以偏移后的顶点Vo中，x，y，z的值为：
x = x + x1 * _Steepness / k * cos(f)
y = _Steepness / k * sin(f)
z = z + z1 * _Steepness / k * cos(f)

搞定了顶点偏移的三维表示，接下来我们该求解法向量了。可知在自定方向波的参与下，x轴z轴都会参与到法线的求解中。
常见的求解思路有两种，一种是沿着波的方向进行求解切线和副切线，一种是依然按照x，z两个方向分别进行求解。（原谅我图示的法线不是画的严格准确的）

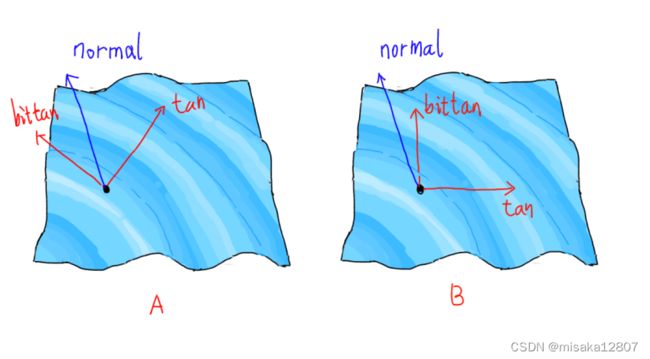
显而易见的是，沿着波方向做切线的求解基本上是不可能的，或者说复杂度高的吓人。依然沿x，z方向求解各自的偏导数的方案，复杂度比较低。因为只给出一条法线的情况下，能够叉乘得出其的两个垂直切线的结果是不唯一的。
沿x方向进行dx求导，得到tangent：
x = 1 - x1 * x1 * _Steepness * sin(f)
y = x1 * _Steepness * cos(f)
z = - z1 * x1 * _Steepness * sin(f)

沿z方向进行dz求导，得到bitangent：
x = - x1 * z1 * _Steepness * sin(f)
y = z1 * _Steepness * cos(f)
z = 1 - z1 * z1 * _Steepness * sin(f)

2.4. 多波叠加

在现实的海面场景中，往往都是多个波进行叠加，各个波之间能够有不同的参数。在原有的设置下，3个参数非常不便于管理。
我们索性用一个四维变量将其整合到一起，并使用一个函数来对这个四维变量进行处理。
)

Properties
    {
    	//其他属性
		_WavwA("wave A: directionX, directionZ, _Steepness, _Wavelength", Vector) = (1, 1, 0.8, 3.0)
	}
float3 gerstner(float4 wave, float3 p, inout float3 tangent, inout float3 bitangent)
{
	///另附
}
v2f vert (appdata v)
     {
         v2f o;
         float3 p = v.vertex;
         float3 tangent = float3(0.0, 0.0, 0.0);
         float3 bitangent = float3(0.0, 0.0, 0.0);
         
         p += gerstner(_WavwA, v.vertex, tangent, bitangent);

         float3 normal = normalize(cross(bitangent, tangent));
         
         //其他变换和属性赋值，阴影计算
         
         return o;
     }

主要是将原有的计算搬到自定义函数里

float3 gerstner(float4 wave, float3 p, inout float3 tangent, inout float3 bitangent)
{
    float k = 2 * UNITY_PI / wave.w;
    float _Amplitude = wave.z / k;
    float c = sqrt(9.8 / k);
    float f = k * ( dot(wave.xy, p.xz) + c * _Time.y);

    tangent += normalize(float3(1 - wave.x * wave.x * k * _Amplitude * sin(f), 
                                        wave.x * k * _Amplitude * cos(f), 
                                        - wave.x * wave.y * k * _Amplitude * sin(f)));

    bitangent += normalize(float3( - wave.y * wave.x * k * _Amplitude * sin(f), 
                                        wave.y * k * _Amplitude * cos(f), 
                                        1 - wave.y * wave.y * k * _Amplitude * sin(f)));
    
    return float3( wave.x * _Amplitude * cos(f), _Amplitude * sin(f), wave.y * _Amplitude * cos(f));
}

完成前置准备后，我们直接在属性中定义两个波，并在顶点着色器中使之相加，即可完成多波叠加。

v2f vert (appdata v)
{
    v2f o;
    float3 p = v.vertex;
    float3 tangent = float3(0.0, 0.0, 0.0);
    float3 bitangent = float3(0.0, 0.0, 0.0);
    
    p += gerstner(_WavwA, v.vertex, tangent, bitangent);
    p += gerstner(_WavwB, v.vertex, tangent, bitangent);

    float3 normal = normalize(cross(bitangent, tangent));
    
    //变换，阴影计算等
}

需要注意的是，多波叠加后，重叠波的问题又会再次出现，我们需要注意让各个波_Steepness的累计和不要超过1，以避免该问题。

2.4.1. 三波叠加

参数如下，一般三个波会采取等比例的波长。


单波作为对比