Machine Learning——sklearn系列(六)——聚类算法(2)
文章目录
- 五、DBSCAN(密度聚类)
-
- 5.1 基础概念
- 5.2 DBSCAN算法优缺点
- 六、Affinity Propagation(AP聚类)
-
- 6.1 算法描述
- 6.2 AP算法选举例子理解:
- 七、Gaussian Mixture model(高斯混合模型GMM)
-
- 7.0 协方差与相关性
- 7.1 高斯模型
- 7.2 高斯混合模型
-
- 7.2.1 EM算法
- 八、谱聚类
- 九、聚类衡量指标(无标签)
-
- 9.1 轮廓系数
- 9.2 CH分数
- 9.3 戴维森堡丁指数(DBI)
- 十、代码
五、DBSCAN(密度聚类)
5.1 基础概念
作为最经典的密度聚类算法,DBSCAN使用一组关于“邻域”概念的参数来描述样本分布的紧密程度,将具有足够密度的区域划分成簇,且能在有噪声的条件下发现任意形状的簇。在学习具体算法前,我们先定义几个相关的概念:
-
邻域:对于任意给定样本x和距离ε,x的ε邻域是指到x距离不超过ε的样本的集合;
-
核心对象:若样本x的ε邻域内至少包含minPts个样本,则x是一个核心对象;
-
边界点:继续以样本为中心,样本领域内没有超过minPts个样本,且它们在之前核心点的区域内,那么它们属于边界点。
-
噪音点(离群点):噪音点就是既不是核心点也不是边界点的第三种情况。
-
密度直达:若样本b在a的ε邻域内,且a是核心对象,则称样本b由样本x密度直达;
-
密度可达:对于样本a,b,如果存在样例p1,p2,…,pn,其中,p1=a,pn=b,且序列中每一个样本都与它的前一个样本密度直达,则称样本a与b密度可达;
-
密度相连:对于样本a和b,若存在样本k使得a与k密度可达,且k与b密度可达,则a与b密度相连。
图示理解上述概念:

x1是核心对象;
x2由x1密度直达;
x3由x1密度可达;
x3与x4密度相连。
ε邻域使用(ε,minpts)这两个关键的参数来描述邻域样本分布的紧密程度,规定了在一定邻域阈值内样本的个数(eps,min_samples)。
5.2 DBSCAN算法优缺点
DBSCAN优点:
不需要事先指定聚类个数,且可以发现任意形状的聚类;
对异常点不敏感,在聚类过程中能自动识别出异常点;
聚类结果不依赖于节点的遍历顺序;
DBSCAN缺点:
对于密度不均匀,聚类间分布差异大的数据集,聚类质量变差;
样本集较大时,算法收敛时间较长;
调参较复杂,要同时考虑两个参数;
离群点。
六、Affinity Propagation(AP聚类)
AP聚类算法是基于数据点间的"信息传递"的一种聚类算法。与k-均值算法或k中心点算法不同,AP算法不需要在运行算法之前确定聚类的个数。AP算法寻找的"examplars"即聚类中心点是数据集合中实际存在的点,作为每类的代表。
6.1 算法描述
假设{x1,x2,⋯,xn}数据样本集,数据间没有内在结构的假设。令S是一个刻画点之间相似度的矩阵,使得s(i,j)>s(i,k)当且仅当xi与xj的相似性程度要大于其与xk的相似性。
AP算法进行交替两个消息传递的步骤,以更新两个矩阵:
- 吸引信息(responsibility)矩阵R:r(i,k)描述了数据对象k适合作为数据对象i的聚类中心的程度,表示的是从i到k的消息;
- 归属信息(availability)矩阵A:a(i,k)描述了数据对象i选择数据对象k作为其据聚类中心的适合程度,表示从k到i的消息。
为了避免振荡,AP算法更新信息时引入了衰减系数λ。每条信息被设置为它前次迭代更新值的λ倍加上本次信息更新值的1-λ倍。其中,衰减系数λ是介于0到1之间的实数。
6.2 AP算法选举例子理解:
S(i,k)就相当于i对选k这个人的一个固有的偏好
r(i,k)表示S(i,k)减去最强竞争对手的评分,可以理解为k对i这个选民的竞争中的优势程度
r(i,k)的更新过程对应选民i对各个参选人的挑选(超出众超有吸引力)
a(i,k):从公式里可以看到,所有r(i‘,k)>0的值都对a有正的加成
即,选民i通过网上关于k的民意调查看到:有很多人(i’)都觉得k不错(r(i‘,k)>0),那么选民i也就会相应的觉得k不错,是个可以相信的选择。
a(i,k)的更新过程对应关于参选人k的民意调查对于选民i的影响。(已经有很多跟随者的人更有吸引力)
两者交替的过程也就可以理解为选民在各个参选人之间不断的比较和不断的参考各个参选人给出的民意调查
r(i,k)的思想反应的是竞争,a(i,k)这是为了让聚类更加成功。
(一群人选总统,总统做演讲,意思是选我比选其他人更好,叫做吸引信息。民众即使候选人也是选民,民众思考到底选谁好,叫做归属信息。反复迭代找到聚类中心。)
七、Gaussian Mixture model(高斯混合模型GMM)
7.0 协方差与相关性
协方差:


协方差的结果的意义:
如果结果为正值,则说明两者是正相关的。
相关性:
(1)当 X, Y 的联合分布像下图那样时,我们可以看出,大致上有: X 越大 Y 也越大, X 越小 Y 也越小,这种情况,我们称为“正相关”。

(2)当X, Y 的联合分布像上图那样时,我们可以看出,大致上有:X 越大Y 反而越小,X 越小 Y 反而越大,这种情况,我们称为“负相关”。

(3)当X, Y 的联合分布像上图那样时,我们可以看出:既不是X 越大Y 也越大,也不是 X 越大 Y 反而越小,这种情况我们称为“不相关”。
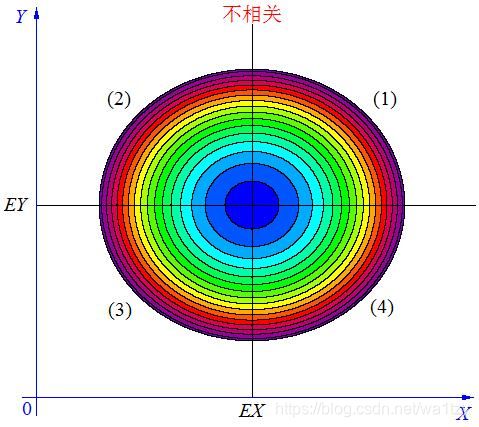
7.1 高斯模型
高斯模型是一种常用的变量分布模型,在数理统计领域有着广泛的应用。
一维高斯分布的概率密度函数如下:

δ均值控制横坐标,方差控制高矮胖瘦(方差大的变得“矮胖”)
7.2 高斯混合模型
高斯混合模型可以看作是由 K 个单高斯模型组合而成的模型,这 K 个子模型是混合模型的隐变量(Hidden variable)。
这里讲一下机器学习和深度学习大多数算法的本质:
比如有很多参数ABCD,最后要求这些参数,思想就是同时求的话比较难(联合概率),我们的方法是固定某些参数去求另外一些参数,这样就比较容易求得这些参数;再固定一些参数求另外得参数,反复迭代,最后这些参数就会精确到确定的值。
比如K-means,随机了两个中心点,中心点位置就固定了,我们来求这些参数的类别,即P(B|A),知道属于哪些类别后,再求P(A|B)。
神经网络也是如此,先随机w,求y,即P(y|w);再固定y,求w,即P(w,y)


假设混合高斯模型由K个高斯模型组成(即数据包含K个类),则GMM的概率密度函数如下:
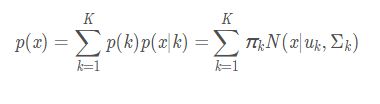

混合高斯模型的本质就是融合几个单高斯模型,来使得模型更加复杂,从而产生更复杂的样本。理论上,如果某个混合高斯模型融合的高斯模型个数足够多,它们之间的权重设定得足够合理,这个混合模型可以拟合任意分布的样本。
7.2.1 EM算法
最大期望算法(Expectation-maximization algorithm,又译为期望最大化算法),是在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量。
EM算法要解决的问题:
极大似然估计的目标是求解实现结果的最佳参数θ,但极大似然估计需要面临的概率分布只有一个或者知道结果是通过哪个概率分布实现的,只不过你不知道这个概率分布的参数。
但现在我们让情况复杂一点,比如这100个男生和100个女生混在一起了。我们拥有200个人的身高数据,却不知道这200个人每一个是男生还是女生,此时的男女性别就像一个隐变量。
这时候情况就有点尴尬,因为通常来说,我们只有知道了精确的男女身高的正态分布参数我们才能知道每一个人更有可能是男生还是女生。反过来,我们只有知道了每个人是男生还是女生才能尽可能准确地估计男女各自身高的正态分布的参数。
而EM算法就是为了解决“极大似然估计”这种更复杂而存在的。
八、谱聚类
要求给K值,affinity(算法):邻近算法、rbf等
九、聚类衡量指标(无标签)
9.1 轮廓系数
metrics.silhouette_score(X, labels)
取值在[-1,1]
9.2 CH分数
metrics.calinski_harabasz_score(X, labels)
取值大于0
9.3 戴维森堡丁指数(DBI)
metrics.davies_bouldin_score(X, labels)
取值[0,1]
十、代码
import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture
from sklearn.datasets import samples_generator# 样本生成器
from sklearn import metrics, cluster #评价方法,聚类库
# X, _ = samples_generator.make_blobs(n_samples=200, centers=2, cluster_std=0.60, random_state=0)
X, y_true = samples_generator.make_moons(200, noise=.05, random_state=0)
# X, y_true = samples_generator.make_circles(200, noise=0.05, random_state=0,factor=0.4)
# gmm = GaussianMixture(n_components=2)
# gmm = cluster.MeanShift()
# gmm = cluster.KMeans(4)
# gmm = cluster.AgglomerativeClustering(2)
# gmm = cluster.AffinityPropagation()
# gmm = cluster.SpectralClustering(2,affinity="nearest_neighbors")
gmm = cluster.DBSCAN(eps=0.3,min_samples=5)
labels = gmm.fit_predict(X)
print(metrics.silhouette_score(X, labels))
print(metrics.calinski_harabasz_score(X, labels))
print(metrics.davies_bouldin_score(X, labels))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis');
plt.show()
参考:
聚类——密度聚类DBSCAN
聚类算法系列之密度聚类DBSCAN
高斯混合模型(GMM)
详解EM算法与混合高斯模型(Gaussian mixture model, GMM)
谱聚类(spectral clustering)原理总结


