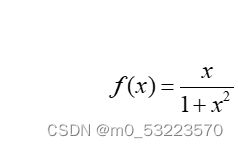【插值】牛顿插值、拉格朗日插值、三次样条插值的Python代码实现
插值简介
插值即根据有限的离散点绘制出穿过所有样本点的曲线,从直观上想象似乎画一条穿过n个特定点的曲线有无数种画法,但从数学意义上来说我们希望画出的曲线能够尽量平滑,震荡幅度尽量小能够在非样本点上符合总体的走势规律,且容易计算。基于这个思想常见的插值方法有拉格朗日插值、牛顿插值以及三次样条插值。本文叙述每种插值的基本特点及代码实现,而对于具体的计算过程用代码给出。
拉格朗日插值与牛顿插值
拉格朗日插值即通过n+1个点可唯一的确定一个n次多项式,牛顿插值也是通过n+1个点的n次多项式,从唯一性可知,两者的插值表达式是一样的,只是计算方式不同。拉格朗日插值是通过基函数进行计算而牛顿插值通过均差表进行计算。两者的主要差别有两点:
- 当使用牛顿插值时,如需增加节点(样本点)不必从头算起,只需要计算最高次项系数即可,原来的计算结果仍可以使用。
- 两者的插值余项(即插值多项式和真实表达式差)不同。
三次样条插值
三次样条插值简称样条插值,是通过一系列形值点的一条光滑曲线,数学上通过求解三弯矩方程组得出曲线函数组的过程。还需要加上两个端点方程才能确定样条多项式,常见的有以下三种:
边界条件1:已知两端一阶导数值,即多项式最左右两端导数值等于某个已知值。
边界条件2:已知两端二阶导数值,即多项式最左右两端二阶导数值等于某个已知值,当左右二阶导数都等于0时称为自然边界条件。
边界条件3:左右两端函数值、一阶导数、二阶导数值相等,这样的样条函数称为周期样条函数。
拉格朗日插值的代码实现
import numpy as np
from sympy import symbols, expand, solve #表达式化简、解矩阵方程组等
import matplotlib.pyplot as plt #绘图
import math
#类的初始化,包括牛顿插值和三次样条插值所需变量
class Interpolation:
def __init__(self, x, y):
self.df = None
self.x = x
self.y = y
self.t = symbols('t') # 定义符号变量
self.n = len(self.x) # 样本点个数
self.spline = np.zeros((self.n, self.n))
self.spline_expression = []
self.results = []
lst = []
self.f = y[0]
self.ln = 0 # 拉格朗日插值表达式
for i in range(self.n):
a = "M" + str(i)
lst.append(a)
self.M = symbols(lst)
self.d = np.ones((self.n))
# 定义拉格朗日插值基函数
def base(self, k):
fm = 1
fz = 1
for i in range(self.n):
if i == k:
continue
fm *= (self.x[k] - self.x[i])
fz *= (self.t - self.x[i])
ans = fz / fm
# print(k, ans)
return ans
# 计算拉格朗日n次多项式
def lagrange(self):
for k in range(self.n):
self.ln += (self.y[k] * self.base(k))
self.ln = expand(self.ln)
return self.ln
# 计算多项式的值
def lagrange_getValue(self, value):
f = self.ln
return f.subs(self.t, value)
牛顿插值的代码实现
代码接在上个代码块后,注意缩进。
# 计算均差表
def diff(self):
length = self.n - 1
self.df = [[0] * length for _ in range(length)]
for j in range(length):
self.df[0][j] = (self.y[j] - self.y[j + 1]) / (self.x[j] - self.x[j + 1])
# print(self.y[j] - self.y[j + 1])
for i in range(1, length):
for j in range(i, length):
self.df[i][j] = (self.df[i - 1][j] - self.df[i - 1][j - 1]) / (self.x[j + 1] - self.x[j - i])
return self.df
# 计算牛顿插值表达式
def Newton(self):
for k in range((self.n - 1)):
tem = self.df[k][k]
for j in range((k + 1)):
tem *= (self.t - x[j])
self.f += tem
self.f = expand(self.f)
return self.f
#计算多项式的值
def Newton_GetValue(self, value):
g = self.f
return g.subs(self.t, value)
三次样条插值代码实现
边界条件1
def spline_boundary_one_sovle(self, b1, b2):
self.spline[0][0], self.spline[0][1] = 2, 1
self.spline[-1][-1], self.spline[-1][-2] = 2, 1
index = 0
for k in range(1, (self.n - 1)):
u = (self.x[k] - self.x[k - 1]) / (self.x[k + 1] - self.x[k - 1])
lam = 1 - u
self.spline[k][index:index + 3] = (u, 2, lam)
index += 1
self.d[0] = 6 / (self.x[1] - self.x[0]) * (self.df[0][0] - b1)
self.d[-1] = 6 / (self.x[-1] - self.x[-2]) * (b2 - self.df[0][-1])
flag = 1
for p in range(1, (self.n - 1)):
self.d[p] = 6 * self.df[1][flag]
flag += 1
print(self.d)
eq = np.dot(self.spline, self.M) - self.d
solver = solve(eq)
for x in solver:
self.results.append(solver[x])
return self.results
三次样条插值计算关键在于通过三弯矩方程解出每一段边界的二阶导数值,再代回积分表达式得到最终表达式。不同的边界条件会对应不同的方程,但积分表达式都是一致的,所以求表达式函数和代入求值函数是通用的。
# 表达式函数
def spline_get_expression(self):
self.spline_expression = []
for j in range((self.n - 1)):
hj = self.x[j + 1] - self.x[j]
exp1 = self.results[j] * (self.x[j + 1] - self.t) ** 3 / 6
exp2 = self.results[j + 1] * (self.t - self.x[j]) ** 3 / 6
exp3 = (self.y[j] - self.results[j] * hj ** 2 / 6) * (self.x[j + 1] - self.t)
exp4 = (self.y[j + 1] - self.results[j + 1] * hj ** 2 / 6) * (self.t - self.x[j])
exp = exp1 + exp2 + exp3 + exp4
exp = exp / hj
exp = expand(exp)
self.spline_expression.append(exp)
return self.spline_expression
#求值函数,不同区间会有不同的表达式,所以需要先确定给的点的所属区间。
def spline_GetValue(self, value):
idx = self.n - 2
for index, element in enumerate(self.x):
if value < element:
idx = index - 1
break
idx = max(idx, 0)
f = self.spline_expression[idx]
f = f.subs(self.t, value)
return f
边界条件2
def spline_boundary_two_solve(self, a, b):
self.spline_boundary_one_sovle(a, b)
self.spline[0][2] = 0
self.spline[-1][-2] = 0
self.d[0] = 2 * a
self.d[-1] = 2 * b
eq = np.dot(self.spline, self.M) - self.d
solver = solve(eq)
self.results = []
for x in solver:
self.results.append(solver[x])
return self.results
边界条件3
def spline_boundary_three_solve(self):
self.spline = np.zeros((self.n - 1, self.n - 1))
self.spline[0][0] = 2
self.spline[0][3] = (self.x[2] - self.x[1]) / (self.x[2] - self.x[0])
self.spline[0][-1] = 1 - self.spline[0][4]
self.spline[-1][0] = (self.x[1] - self.x[0]) / (self.x[-1] - self.x[-2] + self.x[1] - self.x[0])
self.spline[-1][-2] = 1 - self.spline[-1][0]
self.spline[-1][-1] = 2
index = 0
for k in range(1, (self.n - 2)):
u = (self.x[k + 1] - self.x[k]) / (self.x[k + 2] - self.x[k])
lam = 1 - u
self.spline[k][index:index + 3] = (u, 2, lam)
index += 1
self.d = np.ones(self.n - 1)
for i in range(1, (self.n - 1)):
self.d[i] = 6 * self.df[1][i]
self.d[-1] = 6 * (self.df[0][0] - self.df[0][-1]) / (self.x[1] - self.x[0] + self.x[-1] - self.x[-2])
M0 = self.M[0]
del self.M[0]
eq = np.dot(self.spline, self.M) - self.d
solver = solve(eq)
self.results = []
for x in solver:
self.results.append(solver[x])
self.results = [self.results[-1]] + self.results
return self.results
实例演示
假设真实函数为:
取该函数的[-5,5)段进行插值,比较不同插值方式的效果,以1为间隔,取10个点进行插值。则拉格朗日插值和牛顿插值会得到一个9次多项式,三次样条插值会得到9段三次多项式。插值完成后在同样的区间内计算插值与真实值,具体是以0.1为步长取值带入表达式计算。
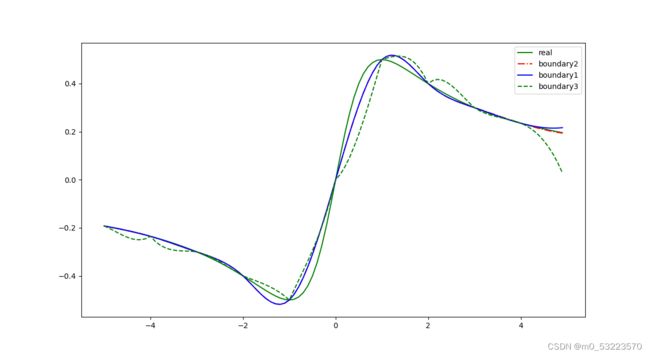
上图展示了不同边界条件下三次样条的插值效果,可以看出三个样条函数的插值效果都还不错,但相比之下第三个边界条件的插值效果只能说差强人意。

上图为拉格朗日插值效果,虽然插值多项式通过了每个插值点,但相比于样条插值震荡情况明显,本例中插值多项式9次项的系数为2.262443438914e-5,虽然很小,当x取值取大一点的值时,插值多项式将很快的增长速度,与真实函数趋近于0的趋势差距巨大。事实上将插值图像多画一段就会有如下的情况:

可以看到,经过多次拐点后这个拉格朗日9次多项式最高次项开始“发力”,远远的偏离了原函数的趋势。
实例代码
if __name__ == "__main__":
xt = np.arange(-5, 5, 1)
yt = np.power(xt, 2) + 1
yt = (1 / yt) * xt
sl = Interpolation(xt, yt)
sl.diff()
print(sl.spline_boundary_one_sovle(-24 / 26 ** 2, -15 / 17 ** 2)) #边界一阶导数值
print(sl.spline_get_expression())
x = np.arange(-5, 5, 0.1)
y = np.power(x, 2) + 1
y = (1 / y) * x
y = y.tolist()
x_spline1 = []
x_spline2 = []
x_spline3 = []
for k in x:
x_spline1.append(sl.spline_GetValue(k))
sl.spline_boundary_two_solve(-220/26**3, 104 / 17**3) # 边界二阶导数值
sl.spline_get_expression()
for k in x:
x_spline2.append(sl.spline_GetValue(k))
sl.spline_boundary_three_solve()
sl.spline_get_expression()
for k in x:
x_spline3.append(sl.spline_GetValue(k))
plt.plot(x, y, "g-", label="real")
plt.plot(x, x_spline2, "r-.", label="boundary2")
plt.plot(x, x_spline1, "b-", label="boundary1")
plt.plot(x, x_spline3, "g--", label="boundary3")
plt.legend()
plt.show()
sl.lagrange()
x_lagrange = []
for k in x:
x_lagrange.append(sl.lagrange_getValue(k))
# 以下注释代码为延长后的拉格朗日多项式
# x =x.tolist()
# xx = x+[4.5,5,6]
# for k in xx:
# x_lagrange.append(sl.lagrange_getValue(k))
plt.plot(x, y, "g-", label="real")
plt.plot(x, x_lagrange, "r-", label="lagrange")
plt.legend()
plt.show()