点云网络的论文理解(二)- PointNet的pytorch复现
1.了解PointNet
为了更好的复现这个东西我们需要先了解这个东西,先把原文给出的图片放在这里,之后我们再一点点理解。

1.1点云的特点
1.1.1无序性:也就是说这个点的先后顺序和实际上是什么无关

你不管这些点加入集合的顺序如何,最后的最后他们组成的图形还是那么个图形,也就是说这些东西的顺序是完全没有必要的。
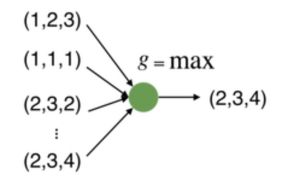
所以我们必须使用对称的函数:
也就是说,这个函数必须要满足,你怎么调换函数变量的输入顺序,函数的计算结果也都不发生变化也就是下图:

所以,我们看一下我们有哪些函数满足这个特点:显然max是满足这个条件的,所以我们可以使用下面的方式来提取点云的特征,但是这样做的话,损失也太大了,所以我们不能如此使用。
所以我们可以使用一个全连接层来扩大维度,这样结果的特征损失就不那么大了。
这样其实我们就完成了一个简单的PointNet。这个东西我们一般将其叫做PointNet(vanilla)
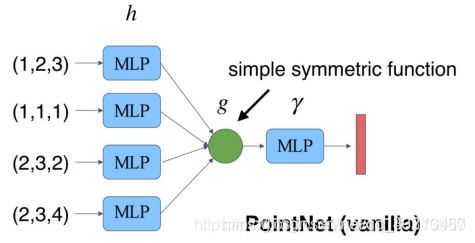
好了说到这里,我们再来仔细看一下原文的图片:

这里其实就是多个全连接层并排放在一起,这样就能达到扩大特征的目的。
1.1.2理论证明
论文中其实有给出理论的证明,大致的意思是:任意一个在Hausdorff空间上连续的函数,都可以被这样的PointNet(vanilla)无限的逼近。但是目前,还没看懂,大家可以自己看一下。
1.2 旋转无关性 也就是说这个一个兔子,你转来转去,他也还是一个兔子

点云的旋转不变性指的是,给予一个点云一个旋转,所有的x , y , z 坐标都变了,但是代表的还是同一个物体
因此对于普通的PointNet(vanilla),如果先后输入同一个但是经过不同旋转角度的物体,它可能不能很好地将其识别出来。在论文中的方法是新引入了一个T-Net网络去学习点云的旋转,将物体校准,剩下来的PointNet(vanilla)只需要对校准后的物体进行分类或者分割即可。
我理解这里是作了这里特殊需要的数据增强,这里需要传入一定量增强之后的数据,因此文章提出来一种新的网络T-Net,因此对于普通的PointNet(vanilla),如果先后输入同一个但是经过不同旋转角度的物体,它可能不能很好地将其识别出来。在论文中的方法是新引入了一个T-Net网络去学习点云的旋转,将物体校准,剩下来的PointNet(vanilla)只需要对校准后的物体进行分类或者分割即可。
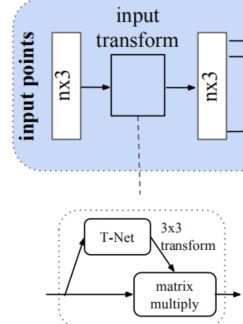
所谓的T-Net也就是下面这个原来的图片中所展示的部分。

由图可以看出,由于点云的旋转非常的简单,只需要对一个N × D 的点云矩阵乘以一个D × D的旋转矩阵即可,因此对输入点云学习一个3 × 3 的矩阵,即可将其矫正;我们可以看到这样的话,其实是对原来的物体进行一个仿射变换,也就是原来的情况将被仿射变换一次。
同样的将点云映射到K维的冗余空间后,再对K维的点云特征做一次校对,只不过这次校对需要引入一个正则化惩罚项,希望其尽可能接近于一个正交矩阵。
因为我们维度变多之后,可能会出现某些权重很大某些权重很小的情况,我们可以将这样的情况理解成我们把某个因素过度看重了,而没有足够重视一些其他因素(其他正常大小的参数在和一个巨大的参数比起来相对就小了),这可能会引起过拟合的问题,所以我们有时候在损失函数中加入一个参数的平方作为一个需要优化的因素来保证参数整体的大小都不太大。
正则化可以参见:
好了,也就是这个小模块就是我们旋转需要的模块。
1.2整个网络的理解
再看一次整体图

之后我们开始逐个块理解:
第一个部分:
下面这个部分是为了旋转原来的图片,将这个图片转的正过来,其实这里不一定真的可以旋转过来,这里只是让其向着正确的方向靠拢。
第二个部分:
这里我们是使用线性全连接层来扩大我们的特征,主要是防止之后maxpooling的时候损失的太多了

第三个部分
这里主要是对新得到的高纬度的信息再进行一次矫正。再尝试将其转正。

第四个部分
这个部分,就是对每个点坐标,再进行一次扩展,让每个点的维度更高。还是使用线性全连接层。

第五个部分
这里就是直接得到了一个全局的特征集合,之后再接上一个网络,让输出顺利完成就是了。(这里后面的网络怎么设计就看你具体是目标识别、目标检测、语义分割等具体的哪个了。)

但是上面这个并没有画明白怎么得到的全局特征。还得看下面那个图:

这里先得看这个n×1088,其实这个一部分是来自于第三部分的输出,一部分来自于第四部分的输出,其实是构成一个小的跳连接,之后再使用线性全连接,逐渐得到你需要的点的特征。
这个东西全部读完之后其实挺神奇的,这个从始至终都是对单个点进行操作的。
2.实现PointNet
2.0我们先引入需要的包
import torch
import torch.nn as nn
import numpy as np
import torch.nn.functional as F
from torch.autograd import Variable
2.1实现一个T-Net:
'''
这里是实现一个T-Net。
这个输入应当是batchsize*3*n_pts(batchsize是点数、n_pts这里的情况是我们xyz这个东西到底需要多少num_feature来进行表示)
输出是一个batchsize*3*3
'''
class T_Net(nn.Module):
def __init__(self):
super(T_Net, self).__init__()
# 这里需要注意的是上文提到的MLP均由卷积结构完成
# 比如说将3维映射到64维,其利用64个1x3的卷积核
self.conv1 = torch.nn.Conv1d(3, 64, 1)
self.conv2 = torch.nn.Conv1d(64, 128, 1)
self.conv3 = torch.nn.Conv1d(128, 1024, 1)
self.fc1 = nn.Linear(1024, 512)
self.fc2 = nn.Linear(512, 256)
self.fc3 = nn.Linear(256, 9)
#因为relu没有参数,所以我们定义一个就行
self.relu = nn.ReLU()
self.bn1 = nn.BatchNorm1d(64)
self.bn2 = nn.BatchNorm1d(128)
self.bn3 = nn.BatchNorm1d(1024)
self.bn4 = nn.BatchNorm1d(512)
self.bn5 = nn.BatchNorm1d(256)
def forward(self, x):
#老操作了,我们使用size取出来一个batch_size
batchsize = x.size()[0]
#下面的卷积其实是一个仿射变换
x = F.relu(self.bn1(self.conv1(x)))
x = F.relu(self.bn2(self.conv2(x)))
x = F.relu(self.bn3(self.conv3(x)))
#这里的2指定的是最后一个维度
x = torch.max(x, 2, keepdim=True)[0]
x = x.view(-1, 1024)
x = F.relu(self.bn4(self.fc1(x)))
x = F.relu(self.bn5(self.fc2(x)))
x = self.fc3(x)
#这里是对对角线的数据进行加强
iden = Variable(torch.from_numpy(np.array([1,0,0,0,1,0,0,0,1]).astype(np.float32)))
iden = iden.repeat(batchsize).view(-1,9)
iden = iden.cuda()
x = x + iden
x = x.view(-1, 3, 3) # 输出为Batch*3*3的张量
return x
实现主体部分
'''
这里是实现一个PointNet的核心部分。
这个输入应当是batchsize*3*1(batchsize是点数),因为一开始过的是一个T_Net -
'''
class PointNetEncoder(nn.Module):
def __init__(self, global_feat = True):
super(PointNetEncoder, self).__init__()
self.tnet = T_Net()
#这里其实是用一个卷积实现了一个全连接的情况
self.conv1 = torch.nn.Conv1d(3, 64, 1)
self.conv2 = torch.nn.Conv1d(64, 128, 1)
self.conv3 = torch.nn.Conv1d(128, 1024, 1)
self.bn1 = nn.BatchNorm1d(64)
self.bn2 = nn.BatchNorm1d(128)
self.bn3 = nn.BatchNorm1d(1024)
self.global_feat = global_feat
def forward(self, x):
'''生成全局特征'''
n_pts = x.size()[2]
#这里是我们旋转之后得到的结果
trans = self.tnet(x)
#这个是我们进行矩阵乘法之前常用的操作
x = x.transpose(2,1)
x = torch.bmm(x, trans) # batch matrix multiply 即乘以T-Net的结果
#当然乘过之后还得换回来
x = x.transpose(2,1)
x = self.conv1(x)
x = F.relu(self.bn1(x))
#这里的pointfeat主要目的就是给一会的跳连接使用的
pointfeat = x
x_skip = self.conv2(x)
x = F.relu(self.bn2(x_skip))
x = self.bn3(self.conv3(x))
x = torch.max(x, 2, keepdim=True)[0]
x = x.view(-1, 1024)
if self.global_feat:
return x, trans
else:
x = x.view(-1, 1024, 1).repeat(1, 1, n_pts)
return torch.cat([x, pointfeat], 1), trans
如果需求为传统分类任务
class PointNetCls(nn.Module):
def __init__(self, k = 2):
super(PointNetCls, self).__init__()
self.k = k
self.feat = PointNetEncoder(global_feat=False)
self.conv1 = torch.nn.Conv1d(1088, 512, 1)
self.conv2 = torch.nn.Conv1d(512, 256, 1)
self.conv3 = torch.nn.Conv1d(256, 128, 1)
self.conv4 = torch.nn.Conv1d(128, self.k, 1)
self.bn1 = nn.BatchNorm1d(512)
self.bn2 = nn.BatchNorm1d(256)
self.bn3 = nn.BatchNorm1d(128)
def forward(self, x):
'''分类网络'''
batchsize = x.size()[0]
n_pts = x.size()[2]
x, trans = self.feat(x)
x = F.relu(self.bn1(self.conv1(x)))
x = F.relu(self.bn2(self.conv2(x)))
x = F.relu(self.bn3(self.conv3(x)))
x = self.conv4(x)
x = x.transpose(2,1).contiguous()
x = F.log_softmax(x.view(-1,self.k), dim=-1)
x = x.view(batchsize, n_pts, self.k)
return x
如果需求为语义分割任务
class PointNetPartSeg(nn.Module):
def __init__(self,num_class):
super(PointNetPartSeg, self).__init__()
self.k = num_class
self.feat = PointNetEncoder(global_feat=False)
self.conv1 = torch.nn.Conv1d(1088, 512, 1)
self.conv2 = torch.nn.Conv1d(512, 256, 1)
self.conv3 = torch.nn.Conv1d(256, 128, 1)
self.conv4 = torch.nn.Conv1d(128, self.k, 1)
self.bn1 = nn.BatchNorm1d(512)
self.bn1_1 = nn.BatchNorm1d(1024)
self.bn2 = nn.BatchNorm1d(256)
self.bn3 = nn.BatchNorm1d(128)
def forward(self, x):
'''分割网络'''
batchsize = x.size()[0]
n_pts = x.size()[2]
x, trans = self.feat(x)
x = F.relu(self.bn1(self.conv1(x)))
x = F.relu(self.bn2(self.conv2(x)))
x = F.relu(self.bn3(self.conv3(x)))
x = self.conv4(x)
x = x.transpose(2,1).contiguous()
x = F.log_softmax(x.view(-1,self.k), dim=-1)
x = x.view(batchsize, n_pts, self.k)
return x, trans