在数据驱动下机械故障诊断的一些方法(一)
机械故障是风力发电设备、航空发动机、高档数控机床等大型机械装备安全可靠运行的“潜在杀手”。故障诊断是保障机械装备安全运行的“杀手锏”。由于诊断的装备量大面广、每台装备测点多、数据采样频率高、装备服役历时长,所以 获取了海量的诊断数据,推动故障诊断领域进入了“大数据”时代。
机械大数据不仅具有大数据的共性,更有本领域的特性:(1)大容量,数据量达到PB级以上,依靠诊断专家和专业技术人员手动分析很不现实,需要新理论与新方法进行自动分析;(2)低密度,机械装备在服役过程中长期处于正常工作状态,导致监测数据蕴含的信息重复性大,数据价值密度低,需要数据提纯;(3)多样性,数据涵盖了多种装备不同工况下多物理源辐射出的大量信息,信息之间相互耦合,导致故障信息表征十分困难;(4)时效性,机械装备各部分紧密关联,微小故障就可能快速引起连锁反应导致装备受损,需要保证数据处理的时效性,高效诊断故障并及时预警。
机械大数据的特性促使故障诊断亟需在现有基础上做出转变,并带来前所未有的机遇。(1)学术思维的转变:由以观察现象、积累知识、设计算法、提取特征、分析决策为主线的传统学术思维转向以机理为基础、数据为中心、计算为手段、智能数据解析与决策为需求的新学术思维。(2)研究对象的转变:由针对齿轮、轴承、转子等机械装备关键零部件的单层次监测诊断转向针对各零部件相互作用、多故障相互耦合的整机装备或复杂系统的多层次监测诊断。(3)分析手段的转变:由人为选择可靠数据、采用信号处理方法提取故障微弱特征的切片式分析手段转向多工况交替变换下、多随机因素影响下智能解析故障整个动态演化过程的全局分析手段。(4)诊断目标的转变:由准确及时识别机械故障萌生与演变,减少或避免重大灾难性事故发生转向利用大数据全面掌控机械装备群的健康动态,整合资源进行智能维护,优化生产环境,保障生产质量,提高生产效率。
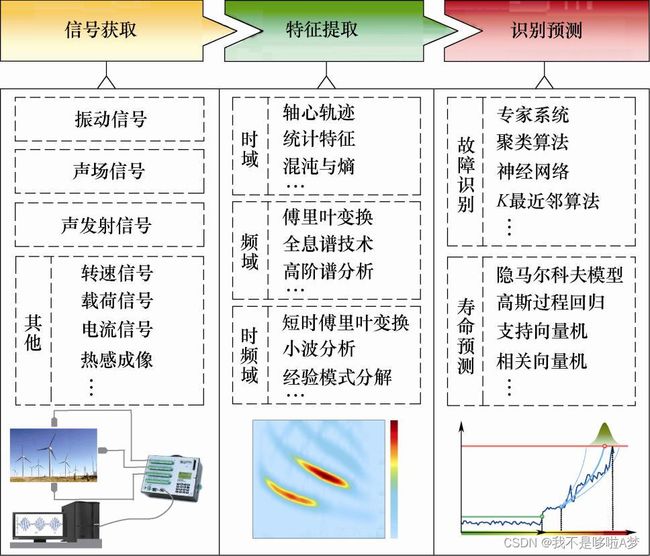
从广义上讲,机械智能故障诊断通常包括如图1所示的三个环节:
(1)信号获取:获取机械装备辐射出的多物理监测信号,反映机械装备的健康状态;
(2)特征提取:通过分析获取的监测数据,提取特征揭示故障信息;
(3)故障识别与预测:基于提取的特征,通过人工智能模型与方法识别并预测故障。
一、信号获取
由于机械装备故障信息常常表现在动力学、声学、摩擦学、热力学等多物理场,利用先进的传感技术获取响应信号表征机械装备的运行状态,是机械故障诊断的前提。
(1)振动信号
设备自身动力学特性外在表现形式之一就是振动,设备的运行状态信息也包含在振动信号之中,因此我们可以通过分析和处理设备的振动信号来判别其运行状态。振动分析法是被广泛应用的故障诊断方法,具有测试和处理简单,诊断结果直观可靠的优势。但是,振动信号容易受到切削时其他因素的影响。
刀具与工件在切削时产生的振动信号与刀具状态改变存在着很高的相关性。伴随着刀具磨损程度的加深,刀具与工件之间的接触面积增大并且表面平整度降低,随着磨损量的变化,振动幅度和频率相应有不同程度的改变。
| 方法 |
原理 |
优缺点及应用 |
| 电测法 |
将被测对象的振动量转换成电量,然后用电量测试仪器进行测量 |
灵敏度高,频率范围及动态、线性范围宽,便于分析和遥测,但易受电磁场干扰,是目前最广泛采用的方法 |
| 机械法 |
利用杠杆原理将振动量放大后直接记录下来 |
抗干扰能力强,频率范围及动态、线性范围窄,测试时会给工件加上一定的负荷,影响测试结果,用于低频大振幅振动及扭振的测量 |
| 光学法 |
利用光杠杆原理、读数显微镜、光波干涉原理,激光多普勒效应等进行测量 |
不受电磁场干扰,测量精度高,适于对质量小及不易安装传感器的试件作非接触测量 |
(2)声音信号
在加工中刀具与工件之间互相摩擦产生声音,在新刀具刚开始执行切削任 务时,其比较锋利并产生的声音较为刺耳;在度过了初期磨损之后,刀具开始正常切削,此阶段是刀具寿命最长的一个阶段,加工产品的废品率最低并且精度都是最高的。在加工过程中,相对而言声音变得平稳;随着刀具磨损程度的加深,磨损量达到一定程度之后,刀具的磨损速度迅速增加,工件的加工质量也是急剧下降,此时声音开始变得很响并且也是变得不平稳。因此,声音对刀具磨损量的变化也是较为灵敏。
但是在一般工况条件下,声音容易受到外界环境的影响,使得采集的数据受到污染,增加后期处理的难度。
(3)声发射信号
金属材料在发生破裂的时候,其内部会释放应变能而产生弹性应力波。刀具在切削时,也会释放应力波,其中必然包含有关刀具磨损信息,借助其监测刀具工作状态。声发射监测技术是一种潜力巨大的新型检测技术,其有效频率一般在 100 kHz以上,可以过滤掉在切削加工中产生的环境的干扰,机床驱动电机的振动干扰等,具有灵敏度高、抗干扰能力强等特点。
(4)切削力信号
切削力信号是指在切削过程中工件与刀具之间产生一种大小相等、方向相反的力,切削力对刀具磨、破损状态的反映十分灵敏。刀具磨损带宽度逐渐增大时,刀具参与切削的表面积也会逐渐增加,切削力发生显著变化。刀具开始逐渐磨损直到破损或磨钝整个周期中,切削力会随之剧烈变化。
(5)电流信号
由于切削力随着刀具磨损的增加而增加,因而机床电动机消耗的电流也相应的增加,电机电流信号被认为比切削力传感器更适合工业制造环境,因为它们的应用相对简单,并且对加工操作没有安装影响,可以直接将电流传感器安装在机床的供电柜里。
(6)主轴功率信号
在数控加工过程中,主轴功率信号的变化可以间接的反映刀具的磨损状态。当刀具出现均匀磨损后,刀具对工件进行加工时就需要更大的力,进而导致机床主轴功率的增大。目前,多数数控机床可以方便的获取到机床加工过程中实时的功率数据,成本较低且可以避免加工中切削、机床振动、刀具温度变化带来的干扰,对生产过程无影响。通过功率传感器直接监控主轴的功率信号,可以实现对刀具均匀磨损状态的监控。但由于功率信号为缓变量且通常情况下采样频率较低,因此其波形信息无法反映出刀具非均匀磨损状态的特征。
二、信号分解/预处理
2.1 信号分解方法
实际机械系统往往同时受到多种复杂激励,因此振动信号包含许多复杂的子信号分量,而其中的某些特征分量与设备运行状态密切相关。例如,当齿轮发生故障时,其振动信号中齿轮啮合频率附近的边带分量的幅值会显著增大。但是,信号中的故障特征分量尤其是早期微弱故障特征极易被噪声和其他无关信号分量淹没,导致设备故障不能被及时发现。因此,利用信号分解方法将振动信号分解为一系列具有明确物理意义的子信号分量,进而从中提取故障特征分量,对机械故障诊断尤为重要。在过去的数十年中,国内外学者发展了许多信号分解方法来提取信号内部的基本组成分量,一些典型的信号分解方法如表2-1所示。
| 方法 |
提出时间 |
基本原理 |
优缺点 |
| 经验模态分解 (Empirical mode decomposition, EMD) |
1998 |
该方法通过迭代“筛选”算法将任意非平稳信号分解为一系列的固有模态函数(IMF) |
EMD是一种完全由数据驱动的自适应分解方法,在机械故障诊断、信号处理等领域得到广泛应用。EMD存在边界效应、模态混叠、对噪声敏感等问题。 |
| 局部均值分解 (Local mean decomposition, LDM) |
2005 |
该方法能自适应地将信号分解为若干乘积函数,乘积函数由一个包络信号和一个纯调频信号相乘得到。 |
相对EMD而言,LDM具有端点效应小、迭代次数少等优势。但是存在平滑次数较多时,信号会发生提前或滞后现象等问题。 |
| 本征时间尺度分解 (Intrinsic time-scale decomposition, ITD) |
2006 |
ITD通过分段方式计算旋转分量在每一个局部时间段上的瞬时频率和瞬时幅值,即可将非平稳信号分解为若干个固有旋转分量和一个单调的趋势分量。 |
ITD在计算效率和计算精度方面都优于EMD。但是该方法抗噪性能较差。 |
| 迭代滤波分解 (Iterative filtering decomposition, IFD) |
2009 |
IFD采用的迭代算法框架与EMD基本一致,但是利用信号低通滤波方式来获取信号均值。 |
在特定条件下能够保证算法收敛,算法稳定性更好。但是IFD在信号分解过程中采用统一的滤波器长度,因此无 法分离频率范围重叠的调频信号分量。 |
| 希尔伯特振动分解方法 (Hilbert vibration decomposition, HVD) |
2006 |
(1)利用Hilbert变换和低通滤波器获取振动信号的平均频率,并将其作为信号主分量的瞬时频率估计值;(2)利用同步解调方法估计主分量幅值;(3)利用估计的频率和幅值重构信号主分量,并将该分量从原始振动信号中减去;(4)重复上述步骤来提取其他能量较弱的信号分量。 |
HVD只适用于信号分量之间能量有显著差异的情况。 |
| 离散小波变换 (Discrete wavelet transform, DWT) |
1998 |
DWT可以正交地将信号分解为低频轮廓部分和高频细节部分,即可视为一个低通滤波器和若干带通滤波器组成的滤波器组。 |
DWT是一种常用的频域信号分解方法,但是在高频部分的频率分辨率较差。 |
| 小波包变换 (Wavelet packet transform, WPT) |
1992 |
WPT将高频细节部分进一步细分,能够得到更高的 频率分辨率。 |
当信号分量实际所在的频率范围与划分的频段不一致时,无法正确分离信号分量。 |
| 经验小波变换 (Empirical wavelet transform, EWT) |
2013 |
首先根据信号傅里叶谱的峰值分布情况确定不同信号分量之间的边界频率(如取相邻两个峰值频率的平均值作为边界频率),从而将信号傅里叶谱划分为不同频段,然后在每一个频段上分别构造小 波滤波器,提取相应的信号分量。 |
当环境噪声很强或者信号分量间隔很近时,EWT很难正确估计各个信号分量的频段范围。 |
| 变分模态分解 (Variational mode decomposition) |
2014 |
VMD假定所有分量都是集中在各自中心频率附近的窄带信号,因此VMD根据分量窄带条件建立约束优化问题,从而估计信号分量的中心频率以及重构相应分量。 |
VMD具有完善的数学理论支撑,其本质是一个自适应最优Wiener滤波器组。但是对于宽带非线性调频信号来说,分量所在的频段往往相互重叠。 |
| 变分模态提取 (Variational mode extraction) |
2018 |
VME建立的基本理论与 VMD相似,但VME将信 号分解成两层——期望模态和残余信号,并基于一个新的准则:残余信号在期望模态的频带内具有尽量少的能量。 |
VME在应用时需要预 先确定期望模态的中心频率初始值,不然提取出的期望模态难以包含有用的信息。 |
2.2 其他预处理方法
2.2.1降噪/去噪
(1)滑动平均法(moving average)
滑动平均法也叫做移动平均法、移动平均值滤波法等等,是一种时间域思想上的信号光滑方法。算法思路为:将该点附近的采样点做算数平均,从而作为这个点光滑后的值。
(2)小波阈值去噪
小波阈值去噪的处理方法一般有:1)强制去噪处理。该方法将小波分解结构中的高频系数全部变为零,即把高频部分全部滤掉,然后对信号进行重构处理;最后得到的去噪信号也比较平滑,但是容易丢失信号的有用成分。2)给定软/硬阈值去噪处理,阈值往往可以通过经验公式获得。
(3)中位值法
中位值法 也叫移动中位数法、中值滤波法等。优点是:在数据采样点密集,且比较平滑的情况下,中位数法可以很好地剔除离群值。缺点是不适用于噪声较大的情况;而且平滑之后,数据光滑度不足;经过中位值法处理之后,极值点会丢失。
(4)标准差法
标准差法的目的是规定一个数据波动阈值,当数据超过这个阈值的时候,便认为该数据离群。这个方法阈值的选取方法,采用窗口数据的3倍标准差。
(5)MAD法
MAD法也是定义了一个阈值,这个阈值叫做中位数绝对偏差MAD。如果超过了3倍的MAD,则认为该数据离群。
2.2.2滤波
(1)空间域和频域滤波器
通常分为四种类型的滤波器——低通、高通、带阻和带通滤波器。具体说明如下:
低通滤波器:只允许通过低频细节,衰减高频细节。
高通滤波器:只允许通过高频细节,衰减低频细节。
带阻滤波器:衰减一定频率范围内的信号。允许低于某个阈值或高于另一个阈值的频率通过。
带通滤波器:只允许特定频带内的信号通过,允许高于低阈值和低于高个阈值的频率通过。
(2)自适应滤波器
根据噪声(或干扰)统计特性在某种误差准则下设计相应的自适应滤波器。常用的误差准则包括最小均方误差、最小二乘、最小方差等。自适应滤波器也可以看作是一种统计信号处理算法,依靠递归方式进行运算。
(3)维纳滤波器
维纳滤波器利用了输入信号与量测信号的统计特性,通过求解维纳-霍夫方程获得在最小均方误差准则下的最优解。但是,维纳滤波器不能对数据进行实时处理,且不适合非平稳的输入信号或者噪声。
(4)卡尔曼滤波器
卡尔曼滤波器是维纳滤波器的发展,它解决了没有期望响应作为参考信号和通信环境为非平稳时的状态估计问题,最早用于随机过程的参数估计,后来很快在各种最优滤波和最优控制问题中得到广泛的应用。卡尔曼滤波器是一种递归滤波算法,能够实现无期望响应下的状态估计。
三、特征提取
当机械装备出现故障时,通常在时域、频域和时频域等维度都有不同程度的体现,以信号处理技术为基础的特征提取是实现机械故障信息表征的主要途径。
| 序号 |
特征参量 |
| 1 |
平均值 (描述信号的稳定中心) |
| 2 |
均方根标准差 (描述信号的分散程度) |
| 3 |
方根幅值 (描述信号的稳定性) |
| 4 |
绝对平均值 (描述信号的平均水平) |
| 5 |
偏斜度 (描述信号偏离程度) |
| 6 |
峭度 (描述波峰的尖锐程度) |
| 7 |
方差 (描述信号的波动程度) |
| 8 |
最大值 (描述信号的波峰) |
| 9 |
最小值 (描述信号的波谷) |
| 10 |
峰峰值 (描述信号的最大值) |
| 11 |
波形指标 (描述信号的波动情况) |
| 12 |
峰值指标 (描述信号波峰系数) |
| 13 |
脉冲指标 (描述信号脉冲系数) |
| 14 |
裕度指标 |
| 15 |
偏斜度指标 (描述信号偏离程度) |
| 16 |
峭度指标 (描述波峰尖锐程度) |
注:上述表格只是列举时域和频域的一部分特征参量,而其他的特征参量可参考一些论文;或者当前热门的是基于神经网络进行特征提取。
四、故障识别与预测
基于特征提取方法能够有效的反映了机械设备故障信息的特征,但是仍需要进一步实行有效的故障分类。因此,分类器也是影响机械故障诊断精度的重要环节,以提取的特征参量作为输入,采用训练好的分类模型去识别这些特征参量携带的故障信息,从而实现机械设备的智能故障诊断分类与寿命预测。
(1)故障识别
K近邻(KNN)作为故障诊断问题中一种基本的分类算法,其本质上是对比已知类别的样本和待分类的样本之间的距离,最后通过设定距离阈值规则对待测样本实现决策分类。但是KNN算法需要预先设定K值,这直接影响到实际的分类精度,且其依赖样本类别的平衡性。
支持向量机(SVM)是一种基于结构风险最小化原则的机器学习模型,适用于小样本的故障分类,该模型在机械设备故障诊断分类有着良好的应用效果。由于SVM是基于线性二分类的样本发展而来,在实际的应用中,海量待分类的数据往往呈现非线性不可分状态,因此需要设计合适的核函数来解决分类问题。
极限学习机(ELM)作为一种单隐含层前馈神经网络的算法,其在训练的过程中对输入层的权重和偏置进行随机赋值,将最优求解问题转化为最小二乘求解问题,从而加快了模型的训练速度。在实际应用中,ELM只需要人为预设隐含层节点数,并且在算法的执行过程中不需要人工调参,避免了传统训练算法不断迭代更新的步骤, 因而ELM模型具有更强的泛化性能、更快的学习速度和计算复杂度更低等优点,大大减少了训练时间。
人工神经网络(ANN)能充分逼近复杂的非线性关系,诊断模型的原理是
通过网络层间的学习建立故障征兆与故障类型的映射关系, 使输入层的节点对应故障征兆, 输出层的节点对应故障类型, 从而实现由故障征兆到故障类型的推理过程。
(2)寿命预测
机械设备剩余寿命预测定义为“机械设备从当前时刻运行至失效状态时刻的时间间隔”,剩余寿命预测是在健康因子组成的性能退化曲线的基础上,预测机械设备从当前时刻运行至失效时刻的时间间隔。目前,剩余寿命预测模型可以分为三大类:基于物理模型的方法、数据驱动的方法和基于混合模型的方法。
基于物理模型的剩余寿命预测方法主要使用机械设备失效机理建立数学模型,描述性能退化过程,开展剩余寿命预测研究。基于物理模型的剩余寿命预测方法深入分析机械设备失效机理,构建性能退化过程物理模型,因此预测结果较为准确。但是随着机械设备结构愈加复杂,难以建立准确的失效机理模型,因此难以得到广泛推广。
数据驱动的剩余寿命预测方法分为两类:基于统计模型的剩余寿命预测方法和基于智能模型的剩余寿命预测方法。1)基于统计模型的剩余寿命预测方法也称为基于经验模型的方法,主要是利用经验知识建立统计模型,然后利用历史观测数据确定模型参数,进而得到机械设备剩余寿命的概率分布函数。2)智能学习模型能够通过智能算法从监测数据中自主学习机械设备性能退化模式,预测剩余寿命,不需要事先构建物理模型或者统计模型,使其逐渐成为研究热点。目前, 在剩余寿命预测领域,常用的智能模型主要包括:人工神经网络模型、支持向量机模型、相关向量机模型。
基于物理模型和数据驱动的剩余寿命预测方法均存在一定的局限性。为了充分发挥两者的优势,人们尝试将两种方法相结合,建立基于混合模型的剩余寿命预测方法。传感器采集到的机械设备状态监测数据无法直接反映其性能退化状态,因此,基于混合模型的剩余寿命预测方法一般先利用数据驱动模型根据监测数据构建反映性能退化过程的健康因子性能退化曲线,然后再利用失效物理模型对机 械设备性能退化曲线建模并预测其剩余寿命。
通过对研究现状的深入分析,结合大数据背景下机械设备健康状态评估及剩余寿命预测所呈现出的显著特点,具体梳理出3点发展趋势:①基于深度学习的机械设备健康因子构建方法;②考虑不确定性的剩余寿命智能预测方法;③小样本条件下剩余寿命预测方法。
参考文献
[1] 雷亚国,贾峰,孔德同,林京,邢赛博. 大数据下机械智能故障诊断的机遇与挑战[J]. 机械工程学报,2018,54(05):94-104.
[2] 陈是扦,彭志科,周鹏. 信号分解及其在机械故障诊断中的应用研究综述[J]. 机械工程学报,2020,56(17):91-107.
[3] 黄豪. 基于振动和切削力信号的刀具磨损状态监测方法研究[D].重庆邮电大学,2022.
[4] 刘会永. 基于振动和功率信号融合的刀具磨损状态监测方法[D].山东大学,2022.
[5] 岑磊. 基于声频特性的卧式钻床病态刀具识别技术研究[D].重庆大学,2021.
[6] 李志猛. 基于声发射信号的铣削状态监测与聚类诊断理论方法研究[D].天津大学,2018.
[7] 陈是扦,彭志科,周鹏. 信号分解及其在机械故障诊断中的应用研究综述[J]. 机械工程学报,2020,56(17):91-107.
[8] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 1998, 454: 903-995.
[9] SMITH J S. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface, 2005, 2(5): 443-454.
[10] REI M G, OSORIO I. Intrinsic time-scale decomposition: time-frequency-energy analysis and real-time filtering of non-stationary signals[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2006, 463(2078): 321-342.
[11] LIN L, WANG Y, ZHOU H. Iterative filtering as an alternative algorithm for empirical mode decomposition[J]. Advances in Adaptive Data Analysis, 2009, 1(4): 543-560.
[12] MALLAT S. A wavelet tour of signal processing[M]. San Diego: Academic Press, 1998.
[13] AKANSU A N, HADDAD R A. Multiresolution signal decomposition:Transforms, subbands, and wavelets[M]. Boston: Academic Press, 1992.
[14] GILLES J. Empirical wavelet transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010.
[15] FELDMAN M. Time-varying vibration decomposition and analysis based on the Hilbert transform[J]. Journal of Sound and Vibration, 2006, 295: 518-530.
[16] Nazari M, Sakhaei S M. Variational mode extraction: a new efficient method to derive respiratory signals from ECG[J]. IEEE Journal of Biomedical and Health Informatics, 2018, 22(4): 1059-1067.
[17] A X Z, A M J Z, B Z L A, et al. Diagnosis of artificially created surface damage levels of planet gear teeth using ordinal ranking[J]. Measurement, 2013, 46(1): 132-144.
[18] DENOEUX T. A k-nearest neighbor classification rule based on Dempster-Shafer theory[J]. IEEE transactions on systems, man, and cybernetics, 1995, 25(5).
[19] 姚德臣, 杨建伟, 程晓卿, 等. 基于多尺度本征模态排列熵和SA-SVM的轴承故障诊断研究[J]. 机械工程学报, 2018, 54(09): 168-176.
[20] HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: A new learning scheme of feedforward neural networks[C]. IEEE International Joint Conference on Neural Networks. IEEE, 2005.
[21] 梁伟阁, 张钢, 王健, 等. 复杂机械设备健康状态预测方法研究综述[J].兵器装备工程学报, 2022, 43(07): 67-77.