全景叙事定位 Towards Real-Time Panoptic Narrative Grounding by an End-to-End Grounding Network 论文阅读笔记

写在前面

  一周时间很快，又到了周末，想想还有很多事情还没干完，但论文还是要继续读的哇。
  这篇论文是 RES 的拓展工作，后续还有一篇新的，在 arxiv v4 版本，感兴趣的可以继续阅读。

• 论文地址：Towards Real-Time Panoptic Narrative Grounding by an End-to-End Grounding Network
• 代码地址：https://github.com/Mr-Neko/EPNG
• 收录于：AAAI 2023
• Ps：2023 年每周一篇博文阅读笔记，主页 更多干货，欢迎关注呀，期待 5 千粉丝有你的参与呦~

一、Abstract

  全景叙事定位 Panoptic Narrative Grounding (PNG) 旨在根据文本描述定位出图像中的相关区域。现有的方法主要基于两阶段的，计算成本非常高。于是本文提出一阶段的网络用于实时的 PNG 任务，名为 End-to-End Panoptic Narrative Grounding network (EPNG)，针对指代目标直接生成 masks。具体来说，提出两种设计：局部感知注意力 Locality-Perceptive Attention (LPA) 和双向语义对齐损失 bidirectional Semantic Alignment Loss (SAL)。LPA 将局部空间先验嵌入注意力模块，即 一个像素可能属于多个尺度下的多个 masks，SAL 使用双向对比损失来归一化模态间的语义一致性。实验表明方法很有效，且 10 倍速度于两阶段模型，同时验证了 EPNG 的 zero-shot 能力。

二、引言

   全景叙事定位 Panoptic Narrative Grounding 需要用二值像素 mask 定位到文本描述的图像目标。如下图所示：

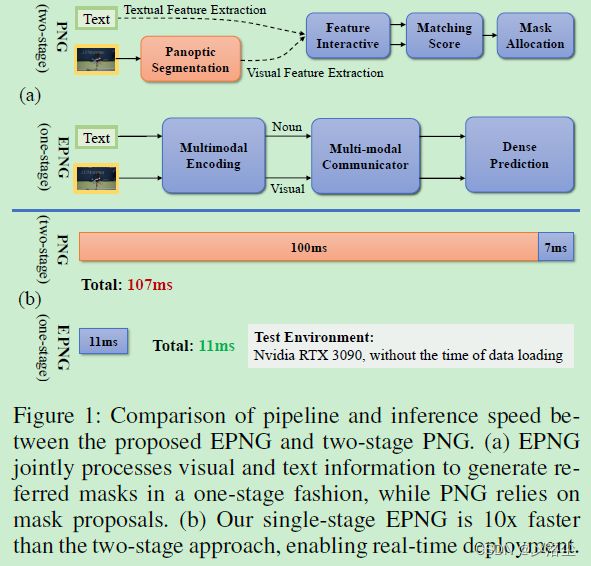
  图 (a) 的两阶段方法，类似 PFPN。首先为给定图像提供一些候选 masks，然后这些 masks 进一步转变为卷积特征，之后进行跨模态的匹配与排序。总体而言，这些两阶段方法将 PNG 定义为一种 mask-text 的匹配问题，减少了预测难度。

  然而这一方法仍然存在两个缺陷：需要离线的特征提取，存储空间和对齐，耗时；预训练的全景分割模型需要大量的 mask 标注。此外，这些全景分割模型的性能限制了 PNG 模型的上界。

  为解决上述问题，需要设计单阶段网络，但存在两个问题：PNG 中的每个像素可以划归到多个 masks 中，这不同于全景分割，需要模型从宏观和微观的角度来捕捉视觉语义。然而现有的方法进关注于全局建模而忽视了局部的信息。其次，相比于其他的定位或分割任务，PNG 涉及了更复杂的关系。在每个样本中，一句表达式的多个名词可能对应着相同的 mask，或者一个名词可能指向多个 masks。于是本文提出一种端到端的全景叙事定位网络 End-to-End Panoptic Narrative Grounding network (EPNG)。贡献总结如下：

• 提出一种实时的端到端全景叙事定位网络，通过统一的跨模态对齐和前项结构中的 mask 预测极大减少了计算消耗；
• 提出两个设计：局部感知注意力 Locality-Perceptive Attention (LPA) 和双向语义对齐损失 bidirectional Semantic Alignment Loss (SAL)，前者增强不同尺度下的视觉特征，后者通过执行像素和名词短语间的对比学习而归一化语义一致性；
• 实验效果很好，且无需额外预训练。

三、相关工作

Panoptic Segmentation

  全景分割的定义，早期的方法：PFPN、Panoptic-DeepLab、PFCN、K-Net、Panoptic SegFormer。得益于这些方法，本文的模型利用词特征作为卷积核在多模态特征上进行卷积，从而生成相应的 masks。

Referring Expression Segmentation

  首先指代表达式分割的定义，早期的方法通过一些通用的分割模型生成一组 proposals，然后从中选择最符合给定短语的一个，缺点是分割模型的性能就是上界。之后是一些单阶段方法的提出，但是假阳性率很高。总结下，RES 是个不完全任务，忽视了 stuff 属性，以及自然语言和图像间的多对多关系，而这是在 Panoptic Narrative Grounding 中考虑到的。

Panoptic Narrative Grounding

  现有的方法采用两步，而本文提出端到端的全景叙事定位方法直接生成名词短语对应的 masks。

四、End-to-End Panoptic Narrative Grounding Network

  

问题定义

  将其视为一个跨模态的稠密预测任务。具体来说，给定一张图像 $\mathrm{I}$ 及相应的文本 $\mathrm{T}$，PNG 的目的是找到名词 $\mathbf{N}=\{n_{\ell }{\}}_{\ell =0}^L$ 所对应的的像素 $i$，其中 $n_{\ell }$ 为第 $\ell$ 个名词，$L$ 表示名词短语的数量。于是 mask 概率可表示为：
$$p\left(\mathrm{M}\right)=\prod _{i\in \mathrm{I}}\prod _{\ell =0}^{L}p\left(i|\mathrm{I},\mathrm{T},n_{\ell }\right)$$

多模态编码

视觉编码器

  给定图像 $\mathrm{I}\in {\mathbb{R}}^{H\times W\times 3}$，首先采用一个视觉 Backbone 提取多尺度视觉特征 ${\mathbf{F}}_{v1}\in {\mathbb{R}}^{\frac{H}{8}\times \frac{W}{8}\times C_1}$，${\mathbf{F}}_{v2}\in {\mathbb{R}}^{\frac{H}{16}\times \frac{W}{16}\times C_2}$，${\mathbf{F}}_{v3}\in {\mathbb{R}}^{\frac{H}{32}\times \frac{W}{32}\times C_3}$，最终得到视觉特征 ${\mathbf{F}}_{\mathbf{v}}\in {\mathbb{R}}^{\frac{H}{16}\times \frac{W}{16}\times C}$：
$${\mathbf{F}}_{\mathbf{v}}=\text{concat}\left[\text{Down}\left({\mathbf{F}}_{v1}\right);{\mathbf{F}}_{v2};\text{Up}\left({\mathbf{F}}_{v3}\right)\right]$$其中 $\text{Up}(\cdot )$ 表示 $2x$ 上采样，$\text{Down}(\cdot )$ 表示 $2x$ 下采样，$[\cdot ]$ 表示特征拼接。

文本编码器

  给定文本 $\mathrm{T}$，采用预训练的 BERT 来提取 word embedding ${\mathrm{F}}_{\mathrm{T}}=\{v_t{\}}_{t=0}^{|T|}$，其中 $v_t$ 表示第 $t$ 个单词的 embedding。之后根据标注滤除掉非名词部分，在每个短语上通过平均池化 word embedding 得到短语特征。这些特征然后经过一个线性层投影到与视觉特征相同的维度。最后短语 embedding 表示为 ${\mathbf{F}}_{\mathbf{N}}=\{f_{n_{\ell }}{\}}_{n_{\ell }=0}^L\in {\mathbb{R}}^{L\times C}$，其中 $n_{\ell }$ 表示第 $\ell$ 个名词短语，$L$ 为短语的长度。

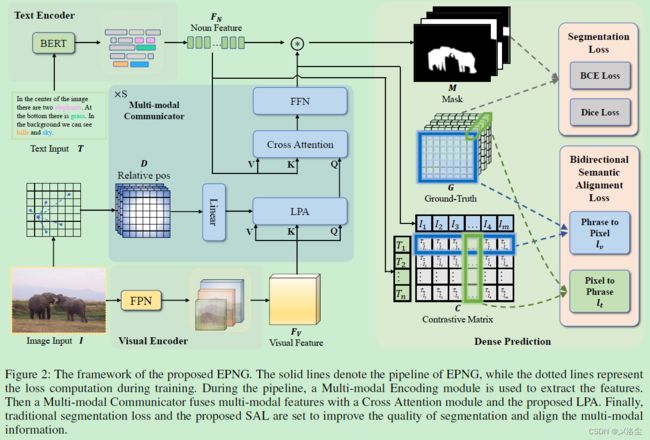
多模态通信器

  基于视觉特征 ${\mathrm{F}}_{\mathrm{v}}$ 和文本特征 ${\mathrm{F}}_{\mathrm{N}}$，设计多模态通信器用于跨模态交互和融合。多模态通信器由 $S$ 个独立层堆叠，每层包含两个模块：局部感知注意力 Locality-Perceptive Attention (LPA) 和跨模态注意力 Cross Attention (CA)。

局部感知注意力

  标准的自注意力平等地对待特征图上的所有 token，而局部感知注意力 LPA 强调关注每个像素的邻居信息。具体来说，在特征 ${\mathrm{F}}^i$ 中，第 $m$ 个和第 $n$ 个向量的 2D 空间坐标表示为 $(x_m,y_m)$ 和 $(x_n,y_n)$，其中下标 $i$ 表示第 $i$ 层的输出特征图。然后计算这两个坐标的欧式距离：
$${\mathrm{D}}_{m,n}=\sqrt{(x_m-x_n{)}^2+(y_m-y_n{)}^2}$$，其中 $\mathrm{D}\in {\mathbb{R}}^{(H\times W)\times (H\times W)}$，其值上界设为 2。之后，在经过 LPA 中的第 $j$ 个头后，将距离矩阵转变为系数矩阵 ${\mathbf{R}}^j\in {\mathbb{R}}^{(H\times W)\times (H\times W)}$：
$${\mathbf{R}}^j={\mathbf{W}}^j\mathbf{D}$$$然后{\mathbf{R}}^j$ 用于注意力的重新加权：
$${\mathbf{A}}^j=\text{Softmax}(\frac{({\mathbf{F}}^i{\mathbf{W}}_Q^j)({\mathbf{F}}^i{\mathbf{W}}_K^j{)}^T}{\sqrt{d_k}}\otimes {\mathbf{R}}^j)$$其中 ${\mathbf{W}}_Q^j\in {\mathbb{R}}^{d\times \frac{d}{h}}$ 和 ${\mathbf{W}}_K^j\in {\mathbb{R}}^{d\times \frac{d}{h}}$ 分别是权重矩阵，$d_k$ 为尺度系数，下标 $j$ 表示第 $j$ 个头，$h$ 设为 8 表示头的数量。$\otimes$ 表示逐元素乘法。

  接下来使用头 $j$ 的注意力结果对特征求和，然后聚合这些结果：
$${\mathrm{Head}}^j={\mathbf{A}}^j({\mathbf{F}}^i{\mathbf{W}}_V^j)$$$$\mathrm{LPA}({\mathbf{F}}^i,{\mathbf{F}}^i,{\mathbf{F}}^i)=\mathrm{concat}({\mathrm{Head}}^1,\cdots ,{\mathrm{Head}}^h){\mathbf{W}}_O$$其中 ${\mathrm{W}}_V^j\in {\mathbb{R}}^{d\times \frac{d}{h}}$ 和 ${\mathbf{W}}_O\in {\mathbb{R}}^{d\times d}$ 为投影矩阵。
$${\mathbf{F}}^{i^{\prime }}=\mathrm{LN}\left(\mathrm{LPA}\left({\mathbf{F}}^i,{\mathbf{F}}^i,{\mathbf{F}}^i\right)+{\mathbf{F}}^i\right)$$其中 $LN(\cdot )$ 表示 layer normalization，在 LPA 模块后应用捷径连接。

LPA 和 多头注意力的区别 (MHA)

  LPA 是基于 MHA 的，但仍有明显不同。MHA 平等地对待特征图中的所有 tokens，并捕捉长范围的依赖。然而局部信息在这一过程中无法避免会被忽略，于是在每个网格内引入距离矩阵的局部先验，这些局部先验能够通过动态调整系数矩阵 ${\mathbf{R}}^j$ 得到。

跨模态注意力

  使用跨模态注意力用于模态间交互：
$${\mathbf{F}}^{i+1}=\mathrm{FFN}\left(\mathrm{LN}\left(\mathrm{MHA}\left({\mathbf{F}}^{i^{\prime }},{\mathbf{F}}_{\mathbf{N}},{\mathbf{F}}_{\mathbf{N}}\right)+{\mathbf{F}}^{i^{\prime }}\right)\right)$$其中 $\mathrm{FFN}(\cdot )$ 表示前项传播网络，${\mathbf{F}}_{\mathbf{N}}$ 为名词特征。

稠密预测

  经过多模态通信器后，得到融合的多模态特征 $F\in {\mathbb{R}}^{\frac{H}{16}\times \frac{W}{16}\times C}$，上采样到 $\frac{H}{4}\times \frac{W}{4}\times C$ 的 Tensor。之后，将每个名词短语特征视为卷积核去卷积 $\mathbf{F}$，从而获得最终的 masks：
$$\mathbf{M}=\mathrm{Up}\left(\mathrm{Sigmoid}\left({\mathbf{F}}_{\mathbf{N}}\ast \mathbf{F}\right)\right)$$其中 $\ast$ 表示卷积操作，Sigmoid 将结果归一化到 $(0,1)$。在上采样后，为 $\mathbf{M}$ 设置一个阈值将其归置到 $\{0,1\}$。

训练损失

  之前分割网络中的分割损失，包含 BCE Loss 和 Dice Loss：
$$L_{BCE}=\sum _{{\hat{y}}_i\in \mathbb{M}}-(y_i\cdot \log (\widehat{y_i})+(1-y_i)\cdot \log (1-\widehat{y_i}))$$其中 ${\hat{y}}_i$ 为第 $i$ 个像素的预测，$y_i$ 为 GT。
$$L_{Dice}=1-\frac{2|M\bigcap G|}{|M|+|G|}$$其中 $M$ 为生成的 mask，$G$ 是 GT，损失值在 $\{0,1\}$ 之间。

  鉴于这些损失函数单为单模态任务设计，于是本文提出一种新的损失，称之为双向语义对齐损失，用于归一化模态间的语义一致性。

双向语义对齐损失 Bidirectional Semantic Alignment Loss

  首先将名词短语视为 anchors 来提升视觉特征的语义一致性：对于第 $i$ 个名词短语 ${\mathbf{F}}_N^i\in {\mathbb{R}}^C$ 和 GT $G^i\in \{0,1{\}}^{H\times W}$，类别为 1 的像素集视为正样本，而 0 的像素集合则为负样本。通过增加正样本集内的一致性，能够强制对齐多模态信息。聚合所有的名词，其损失定义如下：
$$\begin{array}{rl}{l}_v=& \frac{1}{L}\sum _{i=0}^L\frac{1}{|G^{+}|}\sum _{j\in G^{+}}-\log \left(\frac{\exp \left({\mathbf{F}}_n^i\cdot {\mathbf{F}}^j/\tau \right)}{{\sum }_{k\in G}\exp \left({\mathbf{F}}_n^i\cdot {\mathbf{F}}^k/\tau \right)}\right)\end{array}$$其中 $G^{+}$ 为正样本集，表示 GT 内的类别 “1”，$G$ 为 GT，$\tau$ 为温度系数。

  接下来将像素特征视为 anchor 来提升名词特征的语义一致性。损失定义如下：
$$l_t=\frac{1}{|G|}\sum _{i=0}^{|G|}\frac{1}{|T^{+}|}\sum _{j\in T^{+}}-\log \left(\frac{\exp \left({\mathrm{F}}^i\cdot {\mathrm{F}}_n^j/\tau \right)}{{\sum }_{k\in T}\exp \left({\mathrm{F}}^i\cdot {\mathrm{F}}_n^k/\tau \right)}\right)$$其中 $T^{+}|$ 为名词集合的正样本，$T$ 是整个集合，其中 “1” 表示像素属于这一名词短语。组合上面两个损失即可得到 SAL 损失。

  在训练过程中，采用 Dice 损失、BCE 损失、SAL 损失的求和：
$$L={\lambda }_1{L}_{BCE}+{\lambda }_2{L}_{Dice}+{\lambda }_3{L}_{SAL}$$其中 ${\lambda }_1$、${\lambda }_2$、${\lambda }_3$ 为超参数。

五、实验

数据集

  Panoptic Narrative Grounding dataset：13 3103 个训练图像，87 5073 和 5 6531 个分割标注。

实施细节

实验设置

  ResNet-101 作为视觉 Backbone，预训练在 ImageNet 上，BERT 用于文本 Backbone。在训练过程中，冻结 ResNet 层，除最后两层训练。输入图像分辨率 $640\times 640$，最后三层输出的 shape 分别为 $20\times 20\times 256$，$40\times 40\times 256$、$80\times 80\times 256$，文本特征的维度 $768$，8 个注意力头，隐藏维度 $2048$，层的数量为 $S=3$。${\lambda }_1=2$，${\lambda }_2=2$，${\lambda }_3=1$。初始学习率 $\eta =1e^{-5}$，第 5 个 epochs 后衰减一半。在 10 个 epochs 后固定为 $\eta =5e^{-7}$，4 块 RTX 3090（这个还行，能训练），总共 20 个小时，优化器 Adam。

指标

  Average Recall。具体来说，先计算预测的 mask 和 GT 间的 Intersection over Union (IoU)，然后使用完整的 IoU 曲线作为最终的指标。此外还分析 thing\stuff\single\plural。

定量分析

与 SOTA 的比较

  

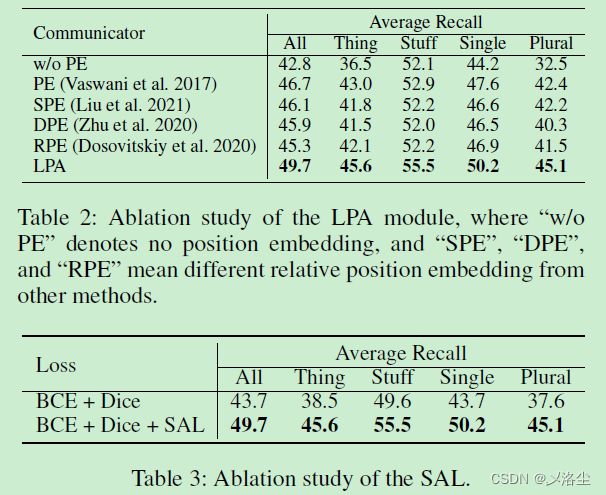
消融研究

  

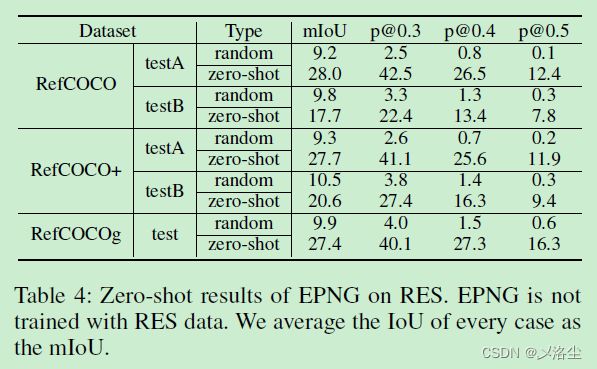
RES 的 Zero-Shot

  

定量分析

可视化

  

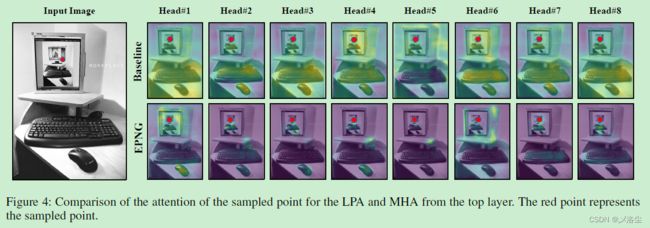
注意力可视化

  

RES 的 Zero-Shot 可视化

  

六、结论

  本文提出一种端到端的全景叙事定位网络 End-to-End Panoptic Narrative Grounding network (EPNG) 用于实时推理。为解决像素和短语的多对多关系，提出 Local-Sensitive Attention (LPA) 和 bidirectional Semantic Alignment Loss (SAL)。实验表明方法性能很强。

写在后面

  这篇文章新颖性够达到 AAAI 的水平了，实验比较充足，中规中矩吧，也不算有特别突出的地方，但也没有明显的短板。