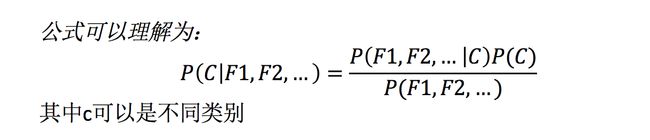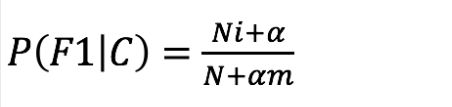朴素贝叶斯算法

1、 什么是朴素贝叶斯分类方法

2、 概率基础

2.1、 概率(Probability)定义

• 概率定义为一件事情发生的可能性
  • 扔出一个硬币，结果头像朝上
  • 某天是晴天
• P(X) : 取值在[0, 1]

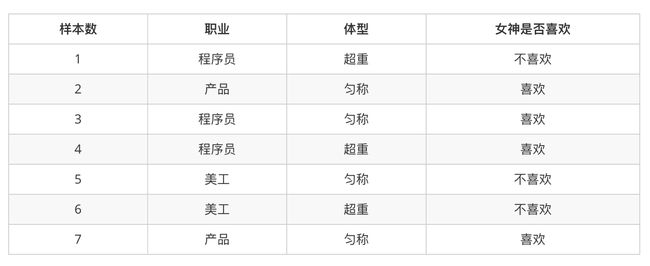
2.2、 女神是否喜欢计算案例

在讲这两个概率之前我们通过一个例子，来计算一些结果：

• 问题如下：
  
  
  那么其中有些问题我们计算的结果不正确，或者不知道计算，我们有固定的公式去计算

2.3、 条件概率与联合概率

• 联合概率：包含多个条件，且所有条件同时成立的概率
  • 记作：P(A,B)
  • 特性：P(A, B) = P(A)P(B)
• 条件概率：就是事件A在另外一个事件B已经发生条件下的发生概率
  • 记作：P(A|B)
  • 特性：P(A1,A2|B) = P(A1|B)P(A2|B)

  注意：此条件概率的成立，是由于A1,A2相互独立的结果(记忆)

• 相互独立：如果P(A,B)=P(A)P(B)，则称事件A与事件B相互独立；

3、 贝叶斯公式

3.1、 公式

• 此时我们再提出一个问题：已知小明是产品经理，体重超重，问是否会被女神喜欢？
  
  根据贝叶斯公式可以得到如下公式：
  
  但是我们发现，分母：P(产品经理,超重) = 0，明显是不对的，因为实际中，超重的产品经理也是有可能被女神喜欢的；

我们先接着往下看，前面是说了贝叶斯公式，却没有说什么是朴素贝叶斯公式，朴素 的意思 就是 特征值之间相互独立的意思；
那么根据相互独立的条件，我们可以将
P(产品经理,超重) = P(产品经理) *P(超重)=2/7 * 3/7 = 6/49

而分子 = P(产品经理,超重|喜欢)*P(喜欢) = P(产品 | 喜欢) * P(超重 | 喜欢)*P(喜欢)
= 1/2 * 1/4 * 4/7
= 1/8 * 4/7
= 4/56
最终P(喜欢 | 产品经理, 超重) = 4/56 / 6/49 = 7/12

7/12，超过了一半，由此可见数据也不是很正确的，一方面，数据是比较少的，另一方面，数据特征不是相互独立的(有关联)，所以值也不是很准!

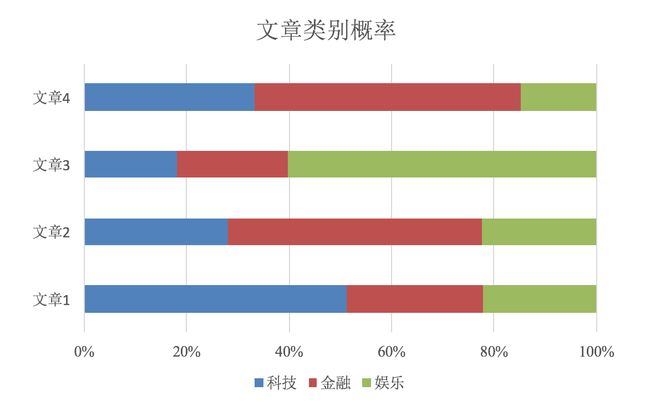
那么这个公式如果应用在文章分类的场景当中，我们可以这样看：

• 朴素贝叶斯 = 朴素 + 贝叶斯

3.2、 应用场景：

• 文本分类：单词作为特征

4、文章分类计算

带入贝叶斯公式求：
求第一题：P(C | Chinese, Chinese, Chinese, Tokyo, Japan)

分子： P(Chinese, Chinese, Chinese, Tokyo, Japan | C) * P( C)
分母：P(Chinese, Chinese, Chinese, Tokyo, Japan )

求第二题：P(非C | Chinese, Chinese, Chinese, Tokyo, Japan)

分子： P(Chinese, Chinese, Chinese, Tokyo, Japan | 非C) * P(非C)
分母：P(Chinese, Chinese, Chinese, Tokyo, Japan )

由此可见，分母是一样的，那我们直接求分子即可！

P( C) = 3/4
第一题分子 = P(Chinese | C) ^3 * P(Tokyo| C) * P(Japan| C) * P( C)

怎么求呢？由前面公式可知：

公式分为三个部分：

• P(C）：每个文档类别的概率(某文档类别数／总文档数量)
• P(W│C)：给定类别下特征（被预测文档中出现的词）的概率
  • 计算方法：P(F1│C)=Ni/N （训练文档中去计算）
    • Ni为该F1词在C类别所有文档中出现的次数
    • N为所属类别C下的文档所有词出现的次数和
• P(F1,F2,…) 预测文档中每个词的概率

P(Chinese | C) = 5/8
但是 P(Tokyo| C) = 0/8 = 0（样本量过少导致），导致整个概率为0了，这明显是不对，那么怎么避免呢？我们往下看：

4.1、 拉普拉斯平滑系数

目的：防止计算出的分类概率为0

• α 指定的系数 一般 为1
• m 为整个训练文档中每个特征词的数量和（每个特征词只算一次）

那么 P(Tokyo| C) = (0 + 1 ) / ( 8 + 6) = 1/14
同理，P(Japan| C) = ( 0+ 1) / ( 8 + 6 ) = 1/14
那从整体来看，P(Chinese | C) ^3 * P(Tokyo| C) * P(Japan| C) * P( C) ， P(Tokyo| C) * P(Japan| C) 都加了拉普拉斯平滑，那么
P(Chinese | C) 也应该加 = (5 + 1) / (8 + 6) = 6 / 14 = 3/7
最终，P(Chinese | C) ^3 * P(Tokyo| C) * P(Japan| C) * P( C) = ( 3 / 7 ) ^ 3 * 1/14 * 1/14 = 27 / 67228
很明显，这个测试集是属于非C的！

5、 朴素贝叶斯API

• sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
  • 朴素贝叶斯分类
  • alpha：拉普拉斯平滑系数

6、案例：20类新闻分类

• 流程
  1. 获取数据
  2. 划分数据集
  3. 特征工程：文本特征抽取
  4. 朴素贝叶斯预估器流程
  5. 模型评估

from sklearn.model_selection import train_test_split
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB


"""
用朴素贝叶斯算法对新闻进行分类
:return:
"""
# 1）获取数据
news = fetch_20newsgroups(subset="all")

# 2）划分数据集
x_train, x_test, y_train, y_test = train_test_split(news.data, news.target)

# 3）特征工程：文本特征抽取-tfidf
transfer = TfidfVectorizer()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)

# 4）朴素贝叶斯算法预估器流程
estimator = MultinomialNB()
estimator.fit(x_train, y_train)

# 5）模型评估
# 方法1：直接比对真实值和预测值
y_predict = estimator.predict(x_test)
print("y_predict:\n", y_predict)
print("直接比对真实值和预测值:\n", y_test == y_predict)

# 方法2：计算准确率
score = estimator.score(x_test, y_test)
print("准确率为：\n", score)

这里的fetch_20newsgroups的数据集要下载：
链接：https://pan.baidu.com/s/1-3xwd3oCSAzx2k7UcejwXg?pwd=hwaq
提取码：hwaq
并按照链接步骤安装即可：安装链接
实际就是将你本机Python安装路径下的：D:\xx\python-3.8.10\Lib\site-packages\sklearn\datasets的_twenty_newsgroups文件按照下方图片修改保存即可使用，注释上面红框框的两行代码，这个下载地址，红框框下并添加一行你的压缩包保存地址，之后保存文件名，就可以在python里面调用数据集了（第一次比较慢，因为要解压）：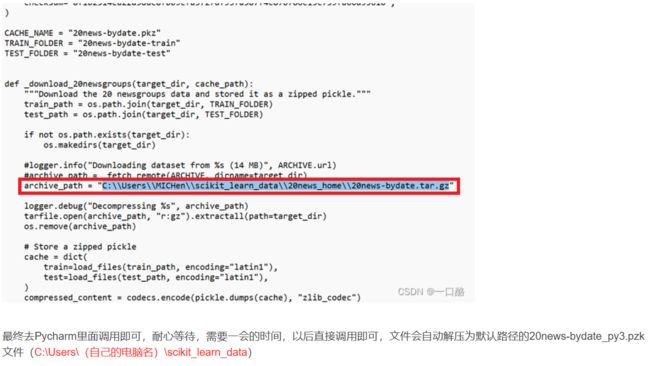

7、总结

• 优点：
  • 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
  • 对缺失数据不太敏感，算法也比较简单，常用于文本分类。
  • 分类准确度高，速度快
• 缺点：
  • 由于使用了样本属性独立性的假设，所以如果特征属性有关联时其效果不好