Xavier Glorot参数初始化: 理解训练Deep DNN的难点

【Reference】
1. Understanding the difficulty of training deep feedforward neural networks

---

0 先前初始化方法

随机初始化权重

初始化策略唯一确知的特性是，初始参数需在不同单元间“破坏对称性”。若具有相同激活函数的两个隐藏单元连接到相同输入，如果它们具有相同的初始参数，应用到确定性损失和确定性的学习算法，它们的参数将一直以相同的方式更新。

我们期望不同神经单元计算不同的函数，如隐藏层的参数矩阵为$W$，隐藏层输入为$x$，而隐藏层输出为$Wx$，为保证各隐藏单元对应函数不同，我们需要使得$W$的行向量具有区分性。

例如，若隐藏层的输入和输出维度相同，可将权重矩阵初始化为正交矩阵，使得每个单元计算不同的函数。通常情况下，每个单元的偏置随机设置启发式常数，如0初始化，此外对于使用ReLU激活函数的网络，为避免激活初始饱和，也可初始化偏置为较小正值如0.1。权重多使用高斯或均匀分布初始化（两者似乎不会有太大区别）。

选择合适的权重初始值

随机初始化权重越大越能破坏对称性，然而初始化权重太大，则可能会使前向传播和反向传播中产生爆炸的值（梯度截断解决），也可能会使单元陷入饱和区，导致梯度消失。

一种初始化m维输入和n维输出的全连接层权重是从均匀分布$U(-\frac{1}{\sqrt{m}},\frac{1}{\sqrt{m}})$中采样，而Glorot and Bengio (2010)建议使用标准化
$$W_{i,j}\sim U\left(-\sqrt{\frac{6}{m+n}},\sqrt{\frac{6}{m+n}}\right)$$

Glorot Uniform初始化所有层，折衷于使其具有相同激活方差和相同梯度方差之间（假设网络不含非线性链式矩阵乘法）。

Saxe et al. (2013)推荐初始化为随机正交矩阵，仔细挑选负责每一层非线性缩放或增益因子g，从而得到用于不同类型的非线性激活函数的特定缩放因子，保证达到收敛所需的训练迭代总数独立于深度。

---

许多实验表明，深度网络比浅层网络更有优势，但在2006年以前，深度网络难以训练，后来一些算法通过改进初始化方法或训练机制，使得深度网络得以训练。这里我们的目标是更好理解，为何使用标准随机梯度下降难以优化参数随机初始化的深度网络？为何最近的一些算法能够训练深度网络？

我们发现，由于sigmoid激活函数均值影响，它会将顶层隐藏层推向饱和（非线性单元饱和较少时往往更有益），因此不适合作为参数随机初始化网络的激活函数。有时饱和单元能够在训练时自行缓慢地离开饱和区，我们解释了有时训练神经网络会看到训练停滞的原因。

本文研究了网络训练时激活函数和梯度在不同层之间的变化，当每一层Jacobian奇异值远小于1时，训练会非常困难。基于以上考虑，我们提出了新型初始化方案，使得训练能够更快收敛。

1 深度神经网络

深度学习方法旨在从低层次特征中学习高层次特征，学习方法不限于：包含多层隐藏层的神经网络、包含多层级隐变量的图模型等。由于这些方法的理论性需求（多受启发于生物学和人类认知），以及其在视觉领域实验成功，目前受到较多关注。也有学者实证，学习高层抽象表征的复杂函数时，往往需要深度架构。

近些年，深度架构的实验结果多来自于可转变为深度监督神经网络的一些模型，但采用的初始化、训练方案不同于经典前馈神经网络。为何这些新颖的算法优于参数使用标准随机初始化并基于梯度优化的监督训练准则？

从对无监督预训练的影响分析可知，作为正则项将参数初始化于一个具有吸引优化程序的“盆地”，其局部极小点具有更好泛化能力。但早期工作表明，即使是一个纯监督、分层程序，也可以取得较好结果。因此，我们不讨论这些算法到底带给了深度网络什么，而是讨论旧的深度网络可能出现的问题。

本文，我们分析训练阶段激活和梯度值在不同层和不同迭代时的变化，同时也评估选择不同激活函数和初始化程序（无监督预训练具有独特的初始化形式）的影响。

2 实验环境和数据集

在线学习无限数据集：Shapeset-3 x 2

研究表明，即使在大训练集，或在线学习下，使用无监督预训练模型参数对模型参数初始化，依然能够获得潜在提升。在线学习关注于优化问题本身，而不是小样本正则化的影响。我们从合成图片数据集Shapeset-3 x 2中采样样本，测试在线学习场景。

有限数据集

• MNIST digits: 50000训练集、10000验证集和10000测试集，28 x 28灰度，10类别。
• CIFAR-10: 50000训练集、10000测试集，32 x 32 x 3彩色，10类别。
• Small-ImageNet: 90000训练集、10000验证集、10000测试集，37 x 37灰度，

实验环境

使用具有1到5层隐藏层的神经网络，隐藏层大小为1000，输出层使用softmax，损失函数使用负对数似然。优化函数使用SGD，mini-batch大小是10。验证隐藏层非线性激活函数：sigmoid、tanh、softsign。

我们搜索学习率和网络深度最优超参数，Shapeset-3 x 2数据集在不同激活函数下的最优深度均为5，使用标准随机初始化方法，初始化每一层的偏置和权重：
$$W_{ij}\sim U\left[-\frac{1}{\sqrt{n}},\frac{1}{\sqrt{n}}\right]\text{\hspace{1em}(1)}$$
式中，$U[-a,a]$是区间$(-a,a)$上的一致分布，$n$是前一层网络的大小（权重矩阵的列数）。

3 训练过程激活函数和饱和的影响

我们想要避免两件事情（可从激活值演变中揭示）：一件是激活函数单方面过饱和（信息无法传播），另一件是单元过线性（不进行任何计算，线性网络拟合能力很弱）。

Sigmoid实验

已证明sigmoid激活函数会减慢学习速度，因为其非零均值会在Hessian矩阵中引入重要奇异值。此处，我们从另一个角度观察深度网络使用sigmoid激活函数的症状。

图2为使用sigmoid作为激活函数的深度网络中，固定300个测试样本在每层网络的激活均值和方差在不同迭代步的变化。

训练开始时，最后一层隐藏层所有sigmoid激活值均被推向低饱和区0，相反，其他隐藏层激活均值在0.5以上，而且从输出层到输入层逐渐减小。

在使用sigmoid激活函数的深度网络中，这种饱和状态会持续相当长的时间。特别地，当网络深度为5的时候，网络无法逃离饱和区，而当深度为4时，网络可以逃离饱和区（图2），与此同时，顶层输出层离开饱和区，而第一层输出层开始进入饱和区，并且保持稳定。

我们假设这种现象由随机初始化使得隐藏单元输出0（位于饱和区）造成，使用预训练模型参数进行初始化不会遭受这种饱和反应。参考假设条件，我们解释是：底层网络的随机初始化值对计算分类任务无任何作用。

初始时刻输出层$\text{softmax}(b+Wh)$，相比通过输入$x$得到的顶层激活值$h$而言（输入$x$不定，初始$h$变化大），更加依赖于偏置$b$（可以更快地学习）。因此，误差梯度倾向于将$Wh$推向0，即$h$推向0。

对称激活函数tanh、softsign输出0时梯度可有效后传，而sigmoid函数输出0时位于饱和区，后传梯度很小，浅层网络参数无法有效更新。训练过程中，顶层隐藏层缓慢离开饱和区，而浅层隐藏层逐渐得到有效更好，学习有用特征。

Tanh实验

由于双曲正切是以0为对称轴的对称函数，初始时刻不会遭受如sigmoid激活函数在顶层隐藏层的饱和现象。然而，若使用式(1)初始化权重，我们观察到训练过程中，从第一层逐渐向上，各隐藏层输出逐渐移至饱和区。

Softsign实验

softsign与tanh相似，但饱和方面表现不同，因为softsign具有平滑渐近线（多项式代替指数）。如图3下图所示，训练过程中，softsign并未出现如tanh一样的饱和现象，初始阶段权重更新很快，并逐渐减慢，最终所有层权重移至更大值。

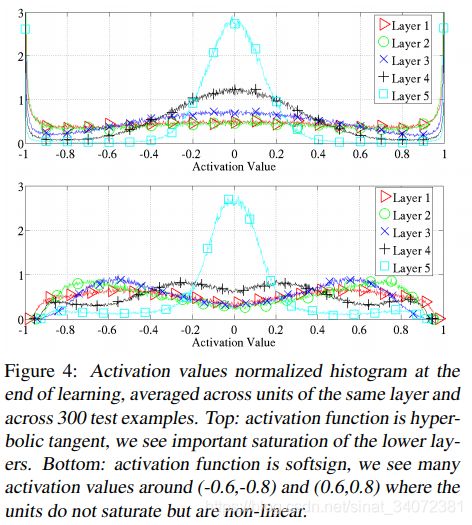
图4所示，训练结束时，softsign激活值与tanh激活值的分布具有很大不同。tanh激活值分布极端，多集中在-1和1，或者0附近；而softsign激活值多集中在线性区0、平坦区-1和1之间梯度可以很好流动的非线性区。

4 研究梯度及其传播

损失函数影响

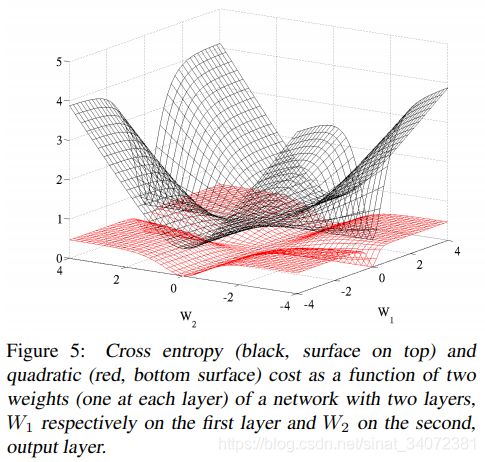
逻辑回归或条件交叉熵损失函数优于传统训练前馈神经网络的二次损失，使用交叉熵损失，训练过程中很少出现停滞。

对于使用对称、0处具有单位导数激活函数的密度神经网络，我们定义$z^i$和$s^i$分别表示第$i$层网络的激活值和激活函数的参数向量，即${\mathbf{s}}^i={\mathbf{z}}^i{W}^i+{\mathbf{b}}^i$，${\mathbf{z}}^{i+1}=f({\mathbf{s}}^i)$，因此
$$\begin{gathered} \frac{\partial Cost}{\partial s_k^i}=f^{\prime }(s_k^i)W_{k,\bullet }^{i+1}\frac{\partial Cost}{\partial {\mathbf{s}}^{i+1}} \\ \frac{\partial Cost}{\partial w_{l,k}^i}=z_l^i\frac{\partial Cost}{\partial s_k^i}\text{\hspace{1em}(2,3)} \end{gathered}$$
方差将根据输入、输出和初始权重任意表示，假设权重参数初始化位于线性区域，权重参数初始化独立，输入特征的方差相同。因此，对于输入为$x$、第$i$层隐藏层单元数为$n_i$的网络：
$$\begin{gathered} f^{\prime }(s_k^i)\approx 1 \\ Var[z^i]=Var[x]\prod _{i^{\prime }=0}^{i-1}{n}^{i^{\prime }}Var[W^{i^{\prime }}]\text{\hspace{1em}(4,5)} \end{gathered}$$

当权重参数与输入独立时
$$Var[Y]=Var[W_1{X}_1+\cdots +W_n{X}_n]=Var[W_1{X}_1]+\cdots +Var[W_n{X}_n]=nVar[W_i]Var[X_i]$$

若第$i^{\prime }$层权重共享标量方差$Var[W^{i^{\prime }}]$，则对于共计包含$d$层的网络：
$$\begin{gathered} Var\left[\frac{\partial Cost}{\partial s_k^i}\right]=Var\left[\frac{\partial Cost}{\partial s^d}\right]\prod _{i^{\prime }=i}^d{n}_{i^{\prime }+1}Var[W^{i^{\prime }}] \\ Var\left[\frac{\partial Cost}{\partial w^i}\right]=\prod _{i^{\prime }=0}^{i-1}{n}_{i^{\prime }}Var[W^{i^{\prime }}]\prod _{i^{\prime }=i}^{d-1}{n}_{i^{\prime }+1}Var[W^{i^{\prime }}]\times Var[x]Var\left[\frac{\partial Cost}{\partial s^d}\right]\text{\hspace{1em}(6,7)} \end{gathered}$$
从前后向传播来看，为保持信息流动，希望对于$\forall (i,i^{\prime })$
$$\begin{gathered} Var[z^i]=Var[z^{i^{\prime }}] \\ Var\left[\frac{\partial Cost}{\partial s^i}\right]=Var\left[\frac{\partial Cost}{\partial s^{i^{\prime }}}\right]\text{\hspace{1em}(8,9)} \end{gathered}$$
对于$\forall i$，上述条件转换为
$$\begin{gathered} n_{i}Var[W^i]=1 \\ {n}_{i+1}Var[W^i]=1\text{\hspace{1em}(10, 11)} \end{gathered}$$
折中两个条件，对于$\forall i$，我们取
$$Var[W^i]=\frac{2}{n_i+n_{i+1}}\text{\hspace{1em}(12)}$$
当所有层具有相同宽度时，公式$(12)$同时满足公式$(10)$和公式$(11)$，如果对于所有权重使用相同的初始化，则所有层的权重梯度相同：
$$\begin{gathered} Var\left[\frac{\partial Cost}{\partial s^i}\right]=[vVar[W]{]}^{d-i}Var[x] \\ Var\left[\frac{\partial Cost}{\partial w^i}\right]=[vVar[W]{]}^{d}Var[x]Var\left[\frac{\partial Cost}{\partial s^d}\right]\text{\hspace{1em}(13,14)} \end{gathered}$$

此时网络与RNN的梯度传播过程类似（相同矩阵连乘），梯度后向传播过程中会出现梯度消失和爆炸现象。

如果使用公式$(1)$标准初始化参数，则所得方差满足
$$nVar[W]=\frac{1}{3}$$

式中，$n$表示所有层隐层单元数量，这将导致后向传播方差的大小依赖于网络总层数（层数越多，方差越小）。

由于归一化参数在所有层间具有连乘影响，因此在初始化深度网络的权重参数时，归一化参数非常重要。为满足我们前后向传播过程中期望方差，我们建议使用以下初始化程序（normalized initialization）：
$$W\sim U\left[-\frac{\sqrt{6}}{\sqrt{n_j+n_{j+1}}},\frac{\sqrt{6}}{\sqrt{n_j+n_{j+1}}}\right]\text{\hspace{1em}(16)}$$

梯度传播研究

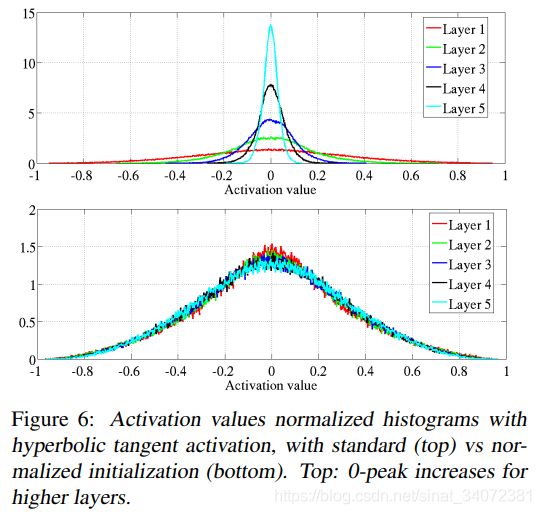
为验证上述理论，我们描绘了使用两种不同参数初始化方法得到的激活值、权重梯度和权重后向传播梯度的归一化直方图，图6-8所示为数据集Shapeset-3 x 2对应的结果（其他数据集结果类似）。

我们监测与第$i$层网络相关的Jacobian矩阵的奇异值：
$$J^i=\frac{\partial {\mathbf{z}}^{i+1}}{\partial {\mathbf{z}}^i}$$

当连续层具有相同隐藏层单元数，平均奇异值与从映射${\mathbf{z}}^i$到${\mathbf{z}}^{i+1}$无穷小的平均比值、从映射${\mathbf{z}}^i$到${\mathbf{z}}^{i+1}$的平均激活方差相关。使用本文提出的初始化方案，比率大约为0.8，使用标准初始化方案，则降至0.5。

学习过程中的后向传播梯度

神经网络的学习动态复杂，由于权重值不再独立于激活值，以及违反线性假设，我们不能使用如前所述的理论假设用于简化方差计算。

从图7可看出，使用标准初始化方案，训练初始阶段的后向传播梯度在向下传播时逐渐减小，但在训练过程中很快逆转，而使用本文提出的权重初始化方案，没有这种后向梯度减小的现象。

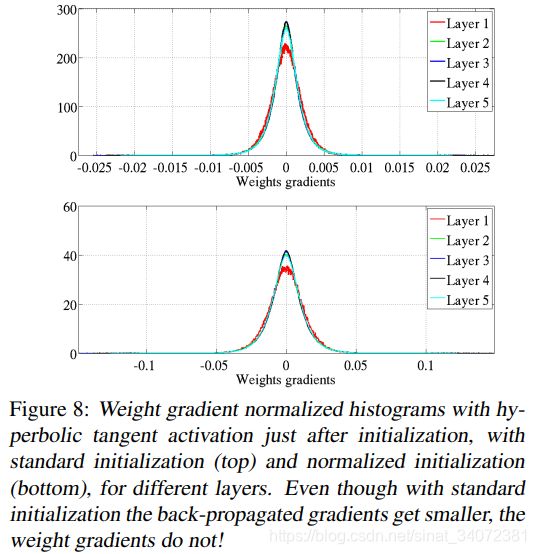
使用标准初始化方案即使后向传播权重梯度变小，但是权重梯度方差在各层之间大致恒定，如图8所示。公式$(10)$可解释这一现象。

如图9所示，使用标准初始化和归一化初始化的权重梯度上在训练过程中发生了改变。实际上，尽管最初梯度相同，但在训练过程中逐渐偏离（低层隐藏层具有更大梯度），使用标准初始化的网络更加明显。

不同层之间权重梯度保持稳定可能是归一化初始化的优势之一，因为不同层之间如果具有非常不同的梯度大小，可能产生病态条件、训练缓慢。最终，我们看到softsign网络与使用归一化初始化的tanh网络相似，如图3下图和图10。

5 误差曲线与结论

训练过程的误差曲线可以很好说明不同策略的优劣，图11为使用不同激活函数的网络在数据Shapeset-3 × 2上在线学习的误差曲线：

表1给出所有数据集下的测试误差：