机器学习可解释性【随机森林规则提取】
引言
目前,机器学习模型应用于各行各业,数据量够多,那就用深度学习吧,数据量少了,传统机器学习算法也能行。
然而机器学习模型作为“黑盒模型”,人们越来越担心其安全性,因而希望模型具有可解释性。
本文主要讲:
- 模型可解释性方案有哪些
- 随机森林规则提取的方法有哪些
- 随机森林规则提取,如何实现
相关工作
模型可解释性方案可分为:
-
事前可解释性建模:
有些模型自带可解释性,如:朴素贝叶斯、线性回归、决策树、基于规则的
模型,针对这些模型,在训练之前,从头设计满足可解释性的模型。 -
事后可解释性分析:
模型已经训练好了,然后再进行解释。
自解释模型本身内置可解释性,如决策树模型,自上而下每条路径代表一条决策,模型可解释性很直观。然而,人类认知有限,自解释模型的内置可解释性受模型复杂度的限制,如果树的深度过深或模型过于复杂,人类也难以理解。但结构太简单,其模型拟合能力必然受限。
在训练后,再解释模型,相对能解决此问题。
即先通过选择最优参数来训练模型,此时得到的结果较好,此时再对“黑盒模型”实施拆箱操作,分析其可解释性,即:事后可解释性分析。
可是,往往可解释性最好的模型并非结果最好。
因而,两种方案都需要权衡取舍。
本文主要介绍随机森林规则提取。
随机森林规则提取
随机森林是基于 Bagging 的集成学习模型,通过集成多棵决策树来提升模型决策能力。随机森林由决策树构成,从决策树的根结点到其叶子节点的一条路径,可以认为是一条由多条 if-then 条件构成的规则。
随机森林规则提取,事前、事后都可以做。主要的算法有:RF+HC 以及 RF+HC_CMPR
这两种算法,重点在于规则筛选方面,区别主要在于 RF+HC_CMPR 在规则打分公式中加入了规则的长度。
本文主要针对已训练好的随机森林模型进行事后可解释性分析,其方法简单易用,赶紧点赞收藏(hhhh,kaiwanxiaola)。
本文的规则提取思路比较简单,步骤如下:
- 训练好随机森林模型
- 遍历随机森林模型中所有子决策树,并提取出所有规则集
- 去除重复规则集
- 通过规则的长度、误差、频率筛选出简化规则集
代码实现
1. 代码解析
save_decision_rules(self,rf, csv_path) :
遍历所有决策树的规则集,并保存。
举个例子,一棵决策树如下图所示:
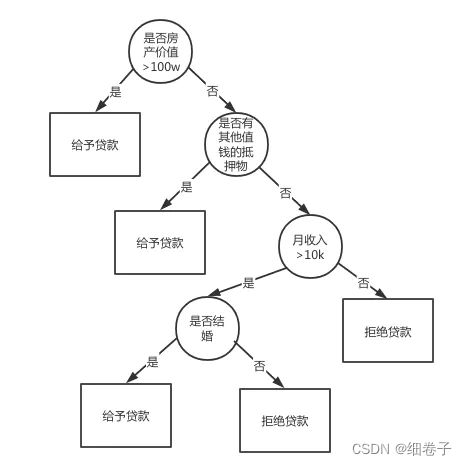
可见,由圆形表示为规则,左边为满足规则,右边为不满足规则,
存储的时候,满足规则,存储为1,不满足规则存储为0,上图中,保存的规则集为:
TREE:0
NODE:0,是否房产价值>100w,4,1
NODE:1,是否有其他值钱的抵押物,4,2
NODE:2,月收入>10k,3,5
NODE:3,是否结婚,4,5
LEAF:4,1
LEAF:5,0
TREE:0 , 表示第0棵决策树
NODE:0, 表示非叶子节点0
LEAF:4, 表示叶子节点4
从上至下为决策树判断过程,如:
NODE:0,是否房产价值>100w,4,1,表示:房产价值>100w,是:跳到编号4,否则:跳到编号1,
编号4,即:LEAF:4,1,即:给予贷款;编号1,即:NODE:1,是否有其他值钱的抵押物,4,2
这样,所有决策树的规则全保存好了。
read_decision_rules(self,path):
从保存文件中,读取所有规则集,即:先遍历左子树,再遍历右子树,
其中,left_tree(self,tree, left,top_feature) 为遍历左子树,
right_tree(self,tree, right, top_feature) 为遍历右子树。
最终得到规则集如下所示:
是否房产价值>100w:1,1
是否房产价值>100w:0,是否有其他值钱的抵押物:1,1
是否房产价值>100w:0,是否有其他值钱的抵押物:0,月收入>10k:1,是否结婚:1,1
是否房产价值>100w:0,是否有其他值钱的抵押物:0,月收入>10k:0,0
是否房产价值>100w:0,是否有其他值钱的抵押物:0,月收入>10k:1,是否结婚:0,0
这样,得到了5条规则集。
filter_rules(self,rules_path):
去除重复规则集
save_rules(self, path):
保存规则集
2. 全部代码实现
import numpy
import config
import constants
import pandas as pd
def getFeatures(_path):
""" 获取特征集 """
df = pd.read_csv(_path)
cols = df.columns.values.tolist()
X = df[cols]
return X.columns
class RFAnalysis():
def __init__(self):
self.l_one_rule,self.r_one_rule = [], []
self.tree_results = []
self.results = [] # 所有树的规则
def save_decision_rules(self,rf, csv_path):
features = getFeatures(csv_path)
txt_path = constants.OS_PATH + '/output/模型解释/随机森林.txt' # 保存路径
with open(txt_path, 'w') as f:
for tree_idx, est in enumerate(rf.estimators_):
tree = est.tree_
assert tree.value.shape[1] == 1 # no support for multi-output
f.write('TREE: {}'.format(tree_idx) + '\n')
print('TREE: {}'.format(tree_idx))
iterator = enumerate(
zip(tree.children_left, tree.children_right, tree.feature, tree.threshold, tree.value))
for node_idx, data in iterator:
left, right, feature, th, value = data
class_idx = numpy.argmax(value[0])
# 写入文件
if left == -1 and right == -1:
print('{} LEAF: return class={}'.format(node_idx, class_idx))
f.write('LEAF:' + str(node_idx) + ',' + str(class_idx) + '\n')
else:
print(
'{} NODE: if feature[{}] < {} then next={} else next={}'.format(node_idx, features[feature],
th,
left, right))
f.write('NODE:' + str(node_idx) + ',' + str(features[feature]) + ',' + str(left) + ',' + str(
right) + '\n')
f.write("#\n") # 每棵树以"#"结束
def left_tree(self,tree, left,top_feature): # 左边:规则
self.r_one_rule.append(top_feature+':0')
line = tree[int(left)]
if line.find("LEAF") != -1: # 叶子节点
l = line.split(",")
value = l[-1]
if len(self.r_one_rule) > 0: # 没有右边的值,就不加
self.r_one_rule.append(value)
_rule = self.r_one_rule.copy()
self.tree_results.append(_rule)
del self.r_one_rule[-1]
del self.r_one_rule[-1]
if line.find('NODE') != -1: # 继续遍历
l = line.split(",")
feature = l[1]
_left = l[2]
_right = l[3]
# 遍历左子树
self.left_tree(tree, _left,feature)
# 遍历右子树
self.right_tree(tree, _right, feature)
def right_tree(self,tree, right, top_feature): # 右边:规则
if top_feature+':0' in self.r_one_rule:
self.r_one_rule.remove(top_feature+':0')
self.r_one_rule.append(top_feature+':1')
line = tree[int(right)]
if line.find("LEAF") != -1: # 叶子节点
l = line.split(",")
value = l[-1]
self.r_one_rule.append(value)
_rule = self.r_one_rule.copy()
self.tree_results.append(_rule)
# del self.r_one_rule[-1]
del self.r_one_rule[-1]
del self.r_one_rule[-1]
if line.find('NODE') != -1: # 继续遍历
l = line.split(",")
feature = l[1]
_left = l[2]
_right = l[3]
# 遍历左子树
self.left_tree(tree, _left,feature)
# 遍历右子树
self.right_tree(tree, _right, feature)
def read_decision_rules(self,path):
trees = []
rules = []
with open(path, 'r') as f:
for line in f:
if line.find('#') != -1:
trees.append(rules)
rules = []
else:
if line.find('TREE:') != -1:
continue
rules.append(line)
for i, tree in enumerate(trees): # 遍历每棵树
self.tree_results = [] # 一棵树的所有规则
root = tree[0]
print(root)
l = root.split(",")
feature = l[1]
left = l[2]
right = l[3]
self.left_tree(tree, left,feature)
self.r_one_rule = []
self.right_tree(tree, right, feature)
self.results.append(self.tree_results)
# print(self.tree_results)
# print(self.results)
def save_rules(self, path):
l = []
with open(path, 'w') as f:
for i, tree in enumerate(self.results):
for j, value in enumerate(tree):
if (len(value) <= 2):
continue
l.append(value)
print(value)
for w,k in enumerate(value):
if w != 0:
f.write(',')
f.write(k)
print(len(l))
def filter_rules(self,rules_path,save_path=""):
""" 规则去重 """
rules = []
with open(rules_path, 'r') as f:
for line in f:
rules.append(line)
rules_copy = rules.copy()
for k,v in enumerate(rules):
r = [i for i,x in enumerate(rules) if x is v]
print(r)
def get_rule_frequency_error(self,csv_path,rules_path,save_path):
""" 计算每条规则频率和误差,并保存在:save_path 中 """
rules = [] # rules:字典:{'尿黄':0}
_id = 0
with open(rules_path, 'r') as f:
for line in f:
rule = {}
l = line.split(",")
label = l[-1].replace('\n', '')
rule['id'] = _id
for i in l[:-1]:
block = i.split(":")
key = block[0]
value = block[1]
rule[key] = value
rule['label'] = label
rules.append(rule)
_id += 1
# print(rules)
df = pd.read_csv(csv_path)
df_len = len(df)
for i, rule in enumerate(rules):
rule['frequency1'] = 0
rule['error1'] = 0
for row in df.itertuples():
is_true = True # 是否有满足规则的样本
for k, value in enumerate(rule):
if value == 'frequency1' or value == 'id' or value == 'error1':
continue
if value == 'label':
row_value = int(getattr(row, constants.ZHENGHOU1))
r = int(rule[value])
if row_value != r:
rule['error1'] = rule['error1'] + 1
continue
row_value = int(getattr(row, value))
r = int(rule[value])
if row_value != r:
is_true = False
break
if is_true:
rule['frequency1'] = rule['frequency1'] + 1 # 满足规则样本数加一
rule['frequency2'] = rule['frequency1'] / df_len
if rule['frequency1'] > 0:
rule['error2'] = rule['error1'] / rule['frequency1']
print(rule['id'],', ',rule['frequency1'])
print(len(rules))
# 存储频率不为0的规则
with open(save_path, 'w') as f:
for i, rule in enumerate(rules):
if rule['frequency1'] == 0:
continue
for k, value in enumerate(rule):
block = value+":"+str(rule[value])
f.write(block)
if value != 'error2':
f.write(',')
f.write('\n')
def get_rank_rules(self,rules_path):
""" 获取规则排序,频率高,误差小 """
rules = []
with open(rules_path, 'r') as f:
for line in f:
rule = {}
l = line.split(",")
last = l[-1].replace('\n', '')
l[-1] = last
is_true = False
is_true_true = False
for i in l:
block = i.split(":")
key = block[0]
value = block[1]
# 筛选频率大于 0。01的
rule[key] = value
if key == 'frequency2' and float(value) > 0.03:
is_true = True
if key == 'error2' and is_true and float(value) < 0.05:
is_true_true = True
if is_true_true:
rules.append(rule)
# print(rules)
ranked_rules = sorted(rules, key=lambda i: i['frequency2'],reverse=True)
for i in ranked_rules:
print(i)
# print(ranked_rules[0:20])
if __name__ == '__main__':
rf_analysis = RFAnalysis()
csv_path = config.PATH
# X_train,X_test,y_train,y_test = data_utils.split(csv_path)
# estimator = models.randomForestClassifier()
# estimator.fit(X_train, y_train)
# 提取并存储规则集
# rf_analysis.save_decision_rules(estimator,csv_path)
# 整理规则集
# txt_path = constants.OS_PATH + '/output/模型解释/随机森林.txt'
# rf_analysis.read_decision_rules(txt_path)
#
# 保存规则集
# save_path = constants.OS_PATH + '/output/模型解释/结果.txt'
# rf_analysis.save_rules(save_path)
# rf_analysis.filter_rules(rules_path=save_path)
# csv_path = constants.OS_PATH + '/output/模型解释/smote.csv'
# 获取规则集
rules_path = constants.OS_PATH + '/output/模型解释/结果.txt'
save_path = constants.OS_PATH + '/output/模型解释/结果_频率_误差.txt'
rf_analysis.get_rule_frequency_error(csv_path,rules_path,save_path)
# rf_analysis.get_rank_rules(rules_path=save_path)
总结
本文首先介绍了机器学习模型可解释性分为:
- 事前可解释性建模
- 事后可解释性分析
随机森林规则提取,既可做事前也可做事后分析。
本文主要针对事后可解释性分析,提出了先通过参数优化建立随机森林模型,然后提取规则集,再将规则集去重,通过误差、频率、长度来筛选规则集。
本文的方法也存在不足,主要在于其筛选方法过于简单,可能筛选不到最佳规则集,同时在算法上,未经优化,循环过多,数据量太大时,较为耗时。
在以后研究中,将加入其他可解释性分析,包括:深度学习可解释性问题。


