【算法分析】实验 1. 基于贪心的会议安排问题

实验内容

本实验要求基于算法设计与分析的一般过程（即待求解问题的描述、算法设计、算法
描述、算法正确性证明、算法分析、算法实现与测试），针对会议安排算法从实践中理解贪
心法的思想、求解策略及步骤。

实验目的

• 理解贪心法的核心思想以及贪心法的求解过程
• 从算法分析与设计角度，对贪心算法有更进一步的理解

环境要求

算法实现可以选择C,java,python,C++等任意的程序设计语言

实验结果

步骤一

理解问题，给出问题的描述：

有n个会议集合 A={1,2,3...n},这些会议都使用的是同一个会议室且在同一时间内最多只有一个会议可以使用该会议室，所以需要根据所有会议举办的时间进行协商。目标是尽可能选择更多的会议来使用资源。

给出每一个会议所占用的时间段，表示形式为 $[b_i , e_i) $ , 其中\(b_i , e_i\)是int型的整数来代表时间。

步骤二

算法设计，包括策略与数据结构的选择,目前可以选择的贪心策略有：

1. 选择最早开始时间且不与已安排会议重叠的会议
2. 选择使用时间最短且不与已安排会议重叠的会议

3. 选择最早结束时间且不与已安排会议重叠的会议

    三个贪心策略中应该选择第三个，因为在这道题的情景之下，贪心的对象应该转化为使剩余时间的可安排时间段尽可能大，以便之后的会议能够有更多的时间来进行。

步骤三

描述算法，用伪代码的方式来描述算法

//A存储的是成对信息 A[i]代表的是第i个会议
//有两个属性，begin开始时间，end结束时间
//num代表的是一共有多少个会议
ARRANGE_MEETING(A,num)
    SORT_ASC(A) //根据end结束时间进行降序排序，如果end相同，则根据begin来进行排序
    NOW_END = A[0].end //选择第一个会议
    CNT=1 //记录选择了几个会议
    for i = 1 to num:
        if A[i].begin >= NOW_END:
            NOW_END = A[i].end
            CNT++
    return CNT;

步骤四

算法的正确性证明

从两个角度对该贪心法进行正确性分析：

1. 最优子结构性质证明

   通过反证法进行证明，将原问题转化为：

   假设B'不是会场安排问题的最优解，那么\(|A_1| > |A’|\)。

   贪心选择会议1后，原问题简化为对C中所有与会议1相容的会议进行安排的子问题。即若A是原问题的一个最优解，则\(A'\)=A-{1}一定是会议安排问题\(C_i\)={i∈C|\(b_i\) ≥ \(e_i\)}的一个最优解。利用反证法，假设\(A'\)不是会场安排问题\(C_1\)的一个最优解，则 |\(A_1\)|>|\(A'\)|。令\(A_2=A_1\))∪{1}，由于\(A_1\)中的会议开始时间均大于等于\(e_1\)，因此\(A_2\)是问题C的一个解。因为|\(A_2\)=\(A_1\){1}|>|\(A'\)∪{1} = A|，所以A不是问题的最优解，与原题设产生矛盾。

2. 贪心选择性质证明

   设C={1,2,…,n}是所给的会议集合，且按结束时间非减序排列。设\(C^*\) 是所给问题的一个最优解，且\(C^*\) 中会议结束时间也按结束时间进行非减序排序\(C^*\) 中的第一个会议是会议 k，如果 k = 1，则就是\(C^*\) 一个以贪心选择的最优解。如果 k > 1，则设\(C’=C^*-{k}∪{1}\)。由于\(e_1 <= e_K\)，且$C^* \(-{k}中任何一个会议都互为相容会议，它们的开始时间都大于等于\)e_k\(，所以\)C^* \(-{k}的开始时间大于等于\)e_1\(，所以C'中的会议也互为相容会议。因此\)|C'| = |C^*|$, \(C^*\)也是最优的。\(C'\)是一个以贪心算法选择活动1开始的最优会议安排。

步骤五

算法复杂性分析，包括时间复杂度和空间复杂度。

1. 时间复杂度

   时间复杂度由两部分构成，分别是排序所需要的时间以及遍历一遍所需要的时间。

   • 排序的复杂度跟采用的算法有关，如果采用冒泡排序，那么复杂度为\(O(n^2)\);如果采用的是快速排序，那么排序部分复杂度为\(O(nlog(n))\)。
   • 遍历一遍所用的时间为\(O(n)\)。

   因为这里直接用的是STL中的快速排序，所以总体的时间复杂度为:\(O(nlog(n))\) 。

2. 空间复杂度

   空间只用了一个变量，所以空间复杂度为\(O(1)\) 。

步骤六

算法的实现与测试，贴上算法运行结果图。

代码：C++版本

#include 
const int maxn = 1000;
using namespace std;
int num;
struct meeting
{
    int b_time;
    int e_time;
    meeting()
    {
        b_time = 0;
        e_time = 0;
    }
};

meeting m[maxn];
queue record;

bool cmp(meeting m1, meeting m2)
{
    if(m1.e_time == m2.e_time)
        return m1.b_time < m2.b_time;
    else
        return m1.e_time < m2.e_time;
}

int main()
{
    cout << "Input the number of the meeting:";
    cin >> num;

    for(int i = 0 ; i < num; i++){
        cin >> m[i].b_time >> m[i].e_time;
    }

    sort(m,m+num,cmp);

    for(int i = 0 ; i < num ; i++){
        cout << m[i].b_time << "," << m[i].e_time << endl;
    }

    int now_e_time = m[0].e_time;
    int cnt = 1;
    record.push(m[0]);

    for(int i = 1 ; i < num ; i++)
    {
        if(m[i].b_time > now_e_time)
        {
            now_e_time = m[i].e_time;
            cnt++;
            record.push(m[i]);
        }
    }

    cout << "Max number of the meeting:" << cnt << endl;

    while(!record.empty())
    {
        meeting head = record.front();
        record.pop();
        cout << head.b_time << "," << head.e_time << endl;
    }

    return 0;
}

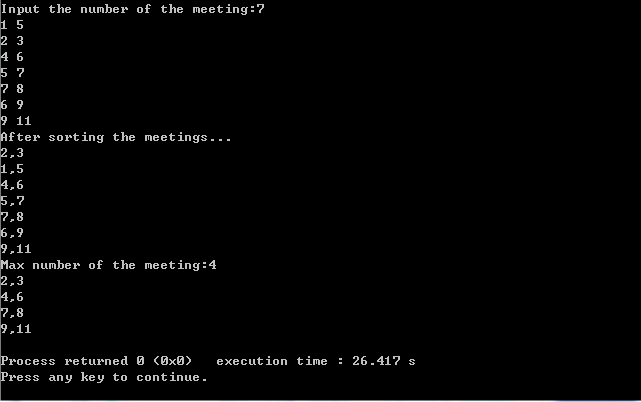
运行结果：

代码：（Python3.6版本）

# -*- coding: utf-8 -*-
"""
Created on Tue Sep 18 17:26:16 2018

@author: pprp
"""

sav = []

def answer(meetings):
    last_end = -1
    ans = 0
    for end,start in sorted((end,start) for start,end in meetings ):
        if start >= last_end:
            last_end = end
            ans += 1
            sav.append([start,end])
    print("最佳安排会议个数为: %s" % ans)
    print("以下为被安排的会议:")
    for a in sav:
        print(a)


meetings = [(2,3),(1,5),(4,6),(5,7),(6,9),(9,11)]

answer(meetings)

运行结果：

runfile('C:/Users/pprp/Desktop/Greedy.py', wdir='C:/Users/pprp/Desktop')
最佳安排会议个数为: 4
以下为被安排的会议:
[2, 3]
[4, 6]
[6, 9]
[9, 11]

实验总结

心得体会与备忘

本次实验是最基础的算法-贪心算法。贪心算法是在对问题求解的时候，总是选取目前情况下的最优选择，而不从整体上加以考虑，做出的决定是局部最优解。虽然贪心算法有时候无法得到整体最优解，但是通常得到的解是比较接近最优解的。贪心算法是采用了自顶向下的思想，将问题规模逐渐缩小，其可以解决的问题通常有两个性质：最优子结构和贪心选择性质。

最优子结构的证明通常需要反证法，需要构造一个原问题和子问题组成的条件。通过假设子问题不是最优解，另外再找一个作为最优解，然后进行反推到原问题，发现矛盾，最终得证。

贪心选择性质的证明需要将问题转化，如果不按照这种策略进行走下去，那么得到的内容就不可能是最优的。如果按照这种策略走下去，那么得到的下一步也一定是最优的解。

与动态规划的关系：

• 动态规划子结构很多问题重复，贪心算法子问题互相独立。
• 贪心算法依赖当前已经做出的选择。
• 两者思路都是自顶向下。
• 动态规划需要将全部子问题解决才能得到结果。
• 贪心算法只要解决一个子问题。

更为详细的对比：来源：https://www.cnblogs.com/batys/p/3322553.html

	标准分治	动态规划	贪心算法
适用类型	通用问题	优化问题	优化问题
子问题结构	每个子问题不同	很多子问题重复（不独立）	只有一个子问题
最优子结构	不需要	必须满足	必须满足
子问题数	全部子问题都要解决	全部子问题都要解决	只要解决一个子问题
子问题在最优解里	全部	部分	部分
选择与求解次序	先选择后解决子问题	先解决子问题后选择	先选择后解决子问题

附录：测试数据

---

输入数据：
7
1 5
2 3
4 6
5 7
7 8
6 9
9 11

排序后数据：
2,3
1,5
4,6
5,7
7,8
6,9
9,11

最佳安排会议的个数:

4

转载于:https://www.cnblogs.com/pprp/p/9880031.html