牛客Leetcode高频题解

01 链表

编号	题目	思路	难度	频率
BM1	反转链表	思路	简单	38.85%
BM2	链表内指定区间反转	思路	中等	27.57%
BM3	链表中的节点每k个一组翻转	思路	中等	36.39%
BM4	合并两个排序的链表	思路	简单	31.88%
BM5	合并k个已排序的链表	思路	较难	33.12%
BM6	判断链表中是否有环	思路	简单	36.46%
BM7	链表中环的入口结点	思路	中等	35.85%
BM8	链表中倒数最后k个结点	思路	简单	32.64%
BM9	删除链表的倒数第n个节点	思路	中等	36.01%
BM10	两个链表的第一个公共结点	思路	简单	37.17%
BM11	链表相加(二)	思路	中等	33.91%
BM12	单链表的排序	思路	中等	45.40%
BM13	判断一个链表是否为回文结构	思路	简单	31.83%
BM14	链表的奇偶重排	思路	中等	43.05%
BM15	删除有序链表中重复的元素-I	思路	简单	36.82%
BM16	删除有序链表中重复的元素-II	思路	中等	32.01%

02 二分查找/排序

编号	题目	思路	难度	频率
BM17	二分查找-I	思路	简单	29.19%
BM18	二维数组中的查找	思路	中等	26.24%
BM19	寻找峰值	思路	中等	27.01%
BM20	数组中的逆序对	思路	中等	17.02%
BM21	旋转数组的最小数字	思路	简单	33.39%
BM22	比较版本号	思路	中等	26.80%

03 二叉树

编号	题目	思路	难度	频率
BM23	二叉树的前序遍历		简单	51.63%
BM24	二叉树的中序遍历		中等	54.38%
BM25	二叉树的后序遍历		简单	64.33%
BM26	求二叉树的层序遍历	思路	中等	45.52%
BM27	按之字形顺序打印二叉树	思路	中等	28.57%
BM28	二叉树的最大深度	思路	简单	60.03%
BM29	二叉树中和为某一值的路径(一)	思路	简单	36.83%
BM30	二叉搜索树与双向链表	思路	中等	31.35%
BM31	对称的二叉树	思路	简单	32.52%
BM32	合并二叉树	思路	简单	68.61%
BM33	二叉树的镜像	思路	简单	65.30%
BM34	判断是不是二叉搜索树	思路	中等	27.23%
BM35	判断是不是完全二叉树	思路	中等	31.66%
BM36	判断是不是平衡二叉树	思路	简单	38.46%
BM37	二叉搜索树的最近公共祖先	思路	简单	42.44%
BM38	在二叉树中找到两个节点的最近公共祖先	思路	中等	42.20%
BM39	序列化二叉树	思路	较难	24.74%
BM40	重建二叉树	思路	中等	27.60%
BM41	输出二叉树的右视图	思路	中等	53.88%

04 堆/栈/队列

编号	题目	思路	难度	频率
BM42	用两个栈实现队列	思路	简单	41.27%
BM43	包含min函数的栈	思路	简单	34.79%
BM44	有效括号序列	思路	简单	30.83%
BM45	滑动窗口的最大值	思路	较难	26.96%
BM46	最小的K个数	思路	中等	27.59%
BM47	寻找第K大	思路	中等	27.86%
BM48	数据流中的中位数	思路	中等	29.35%
BM49	表达式求值	思路	中等	38.99%

05 哈希

编号	题目	思路	难度	频率
BM50	两数之和	思路	简单	34.76%
BM51	数组中出现次数超过一半的数字	思路	简单	32.74%
BM52	数组中只出现一次的两个数字	思路	中等	52.17%
BM53	缺失的第一个正整数	思路	中等	33.63%
BM54	三数之和	思路	中等	22.65%

06 递归/回溯

编号	题目	思路	难度	频率
BM55	没有重复项数字的全排列	思路	中等	53.80%
BM56	有重复项数字的全排列	思路	中等	35.77%
BM57	岛屿数量	思路	中等	38.95%
BM58	字符串的排列	思路	中等	23.33%
BM59	N皇后问题	思路	较难	41.68%
BM60	括号生成	思路	中等	51.69%
BM61	矩阵最长递增路径	思路	中等	32.31%

07 动态规划

编号	题目	思路	难度	频率
BM62	斐波那契数列	思路	入门	36.47%
BM63	跳台阶	思路	简单	40.26%
BM64	最小花费爬楼梯	思路	简单	41.86%
BM65	最长公共子序列(二)	思路	中等	32.29%
BM66	最长公共子串	思路	中等	32.84%
BM67	不同路径的数目(一)	思路	简单	44.18%
BM68	矩阵的最小路径和	思路	中等	48.13%
BM69	把数字翻译成字符串	思路	中等	17.15%
BM70	兑换零钱(一)	思路	中等	34.76%
BM71	最长上升子序列(一)	思路	中等	25.39%
BM72	连续子数组的最大和	思路	简单	39.42%
BM73	最长回文子串	思路	中等	36.05%
BM74	数字字符串转化成IP地址	思路	中等	34.49%
BM75	编辑距离(一)	思路	较难	42.05%
BM76	正则表达式匹配	思路	较难	27.07%
BM77	最长的括号子串	思路	较难	24.68%
BM78	打家劫舍(一)	思路	中等	36.16%
BM79	打家劫舍(二)	思路	中等	37.77%
BM80	买卖股票的最好时机(一)	思路	简单	51.93%
BM81	买卖股票的最好时机(二)	思路	中等	61.25%
BM82	买卖股票的最好时机(三)	思路	较难	42.26%

08 字符串

编号	题目	思路	难度	频率
BM83	字符串变形	思路	简单	22.33%
BM84	最长公共前缀	思路	简单	31.48%
BM85	验证IP地址	思路	中等	19.66%
BM86	大数加法	思路	中等	39.35%

09 双指针

编号	题目	思路	难度	频率
BM87	合并两个有序的数组	思路	简单	35.80%
BM88	判断是否为回文字符串	思路	入门	59.27%
BM89	合并区间	思路	中等	26.98%
BM90	最小覆盖子串	思路	较难	26.72%
BM91	反转字符串	思路	入门	65.44%
BM92	最长无重复子数组	思路	中等	30.55%
BM93	盛水最多的容器	思路	中等	39.59%
BM94	接雨水问题	思路	较难	39.94%

010 贪心算法

编号	题目	思路	难度	频率
BM95	分糖果问题	思路	较难	22.93%
BM96	主持人调度（二）	思路	中等	22.87%

11 模拟

编号	题目	思路	难度	频率
BM97	旋转数组	思路	中等	42.30%
BM98	螺旋矩阵	思路	简单	27.46%
BM99	顺时针旋转矩阵	思路	中等	51.14%
BM100	设计LRU缓存结构	思路	较难	41.36%
BM101	设计LFU缓存结构	思路	较难	30.80%

反转链表

(1)使用栈解法：

import java.util.Stack;
public class Solution {
  public ListNode ReverseList(ListNode head) {
      Stack<ListNode> stack= new Stack<>();
      //把链表节点全部摘掉放到栈中
      while (head != null) {
          stack.push(head);
          head = head.next;
      }
      if (stack.isEmpty())
          return null;
      ListNode node = stack.pop();
      ListNode dummy = node;
      //栈中的结点全部出栈，然后重新连成一个新的链表
      while (!stack.isEmpty()) {
          ListNode tempNode = stack.pop();
          node.next = tempNode;
          node = node.next;
      }
      //最后一个结点就是反转前的头结点，一定要让他的next
      //等于空，否则会构成环
      node.next = null;
      return dummy;
  }
}

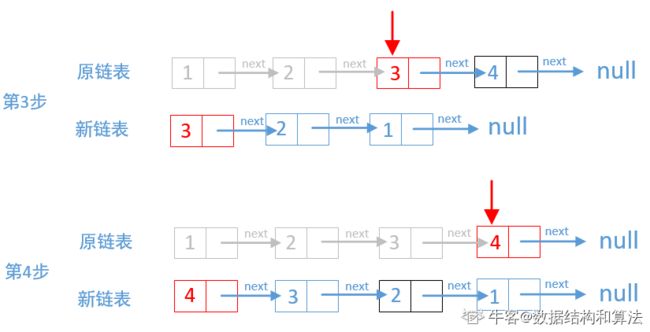
(2)双链表解法：

public ListNode ReverseList(ListNode head) {
    //新链表
    ListNode newHead = null;
    while (head != null) {
        //先保存访问的节点的下一个节点，保存起来
        //留着下一步访问的
        ListNode temp = head.next;
        //每次访问的原链表节点都会成为新链表的头结点，
        //其实就是把新链表挂到访问的原链表节点的
        //后面就行了
        head.next = newHead;
        //更新新链表
        newHead = head;
        //重新赋值，继续访问
        head = temp;
    }
    //返回新链表
    return newHead;
}

(3)双指针解法：

public class Solution {
  public ListNode ReverseList(ListNode head) {
   if(head == null){
       return null;
   }
   ListNode p1 = null;
   ListNode p2 = head;
   ListNode p3 = head.next;
   while(p2 != null){
       p2.next = p1;
       p1 = p2;
       p2 = p3;
       if(p3 != null){
           p3 = p3.next;
       }
   }
   return p1;
  }
}

链表内指定区间反转

(1)递归解法:

import java.util.*;
public class Solution {
    ListNode temp = null;
    public ListNode reverse(ListNode head, int n){
        //只颠倒第一个节点，后续不管
        if(n == 1){ 
            temp = head.next;
            return head;
        }
        //进入子问题
        ListNode node = reverse(head.next, n - 1); 
        //反转
        head.next.next = head;
        //每个子问题反转后的尾拼接第n个位置后的节点
        head.next = temp; 
        return node;
    }
    
    public ListNode reverseBetween (ListNode head, int m, int n) {
        //从第一个节点开始
        if(m == 1) 	return reverse(head, n);
        //缩减子问题
        ListNode node = reverseBetween(head.next, m - 1, n - 1); 
        //拼接已翻转
        head.next = node;
        return head;
    }
}

(2)头插法迭代：

import java.util.*;
public class Solution {
    public ListNode reverseBetween (ListNode head, int m, int n) {
        //加个表头
        ListNode res = new ListNode(-1); 
        res.next = head;
        //前序节点
        ListNode pre = res; 
        //当前节点
        ListNode cur = head; 
        //找到m
        for(int i = 1; i < m; i++){ 
            pre = cur;
            cur = cur.next;
        }
        
        //从m反转到n
        ListNode temp = null;
        for(int i = m; i < n; i++){ 
            temp = cur.next;
            cur.next = temp.next;
            temp.next = pre.next;
            pre.next = temp;
        }
        //返回去掉表头
        return res.next; 
    }
}

排序

（1）冒泡排序 （2）快速排序 ```java import java.util.*; public class Solution { /** * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可 * 将给定数组排序 * @param arr int整型一维数组 待排序的数组 * @return int整型一维数组 */ public int[] MySort (int[] arr) { quickSort(arr , 0 , arr.length-1); return arr; } public void quickSort(int[] list, int left, int right) { if (left < right) { // 分割数组，找到分割点 int point = partition(list, left, right); // 递归调用，对左子数组进行快速排序 quickSort(list, left, point - 1); // 递归调用，对右子数组进行快速排序 quickSort(list, point + 1, right); } }

/**
 * 分割数组，找到分割点
 */
public int partition(int[] list, int left, int right) {
    // 用数组的第一个元素作为基准数
    int first = list[left];
    while (left < right) {
        while (left < right && list[right] >= first) {
            right--;
        }

        // 交换
        swap(list, left, right);

        while (left < right && list[left] <= first) {
            left++;
        }

        // 交换
        swap(list, left, right);
    }
    // 返回分割点所在的位置
    return left;
}

private void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

}

（3）归并排序MergeSort

![图片说明](https://img-blog.csdnimg.cn/img_convert/6402e08ab806349a985b2a810dcc1a73.png)

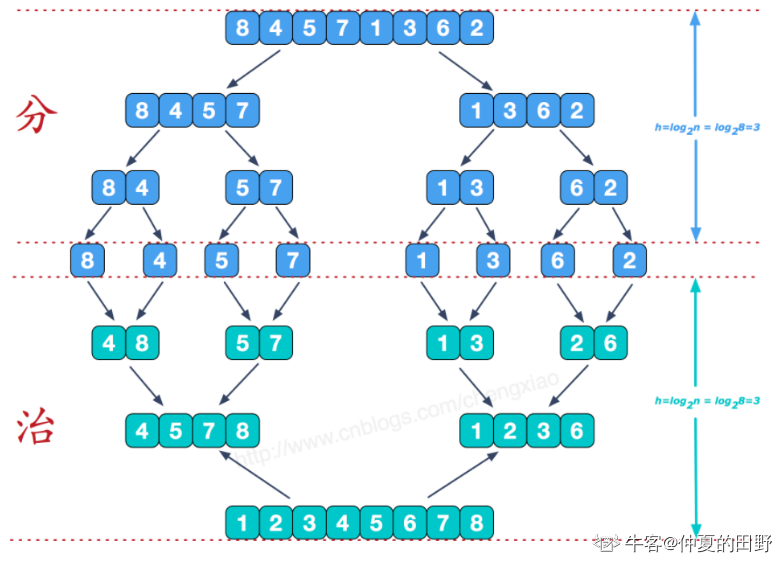
```java
import java.util.*;
public class Solution {
  /**
   * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
   * 将给定数组排序
   * @param arr int整型一维数组 待排序的数组
   * @return int整型一维数组
   */
  public int[] MySort (int[] arr) {
      mergeSort(arr,0,arr.length-1);
      return arr;
  }

  public void mergeSort(int[] arr,int l,int r){
      if(l==r){
          return;
      }
      int mid = l+((r-l)>>1); //中点位置，即(l+r)/2
      mergeSort(arr,l,mid);
      mergeSort(arr,mid+1,r);
      merge(arr,l,mid,r);
  }

  public void merge(int[] arr,int l,int mid,int r){
      int [] help= new int[r-l+1];    //辅助数组
      int i=0;
      int p1=l; //左半数组的下标
      int p2=mid+1; //右半数组的下标

      //判断是否越界
      while(p1<=mid && p2<=r){
          help[i++]=arr[p1]

（4）堆排序

   public int[] MySort (int[] arr) {
       heapSort(arr);
       return arr;
   }

   public static void heapSort(int[] arr){
       if(arr == null || arr.length<2){
           return;
       }
       for(int i=0;i<arr.length;i++){
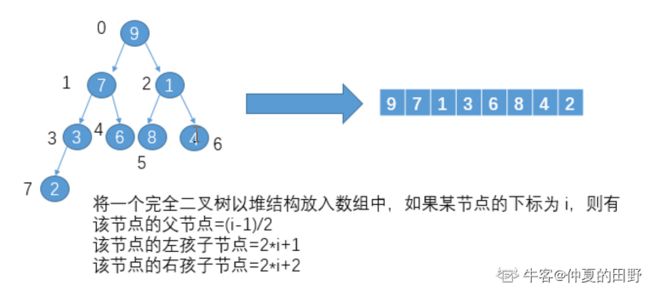
           heapInsert(arr,i); //构造完全二叉树
       }
       int size = arr.length;
       swap(arr,0,--size);
       while(size>0){
           heapify(arr,0,size);// 最后一个数与根交换
           swap(arr,0,--size);
       }

   }
   //判断该结点与父结点的大小，大结点一直往，建立大根堆
   public static void heapInsert(int[] arr,int index){
       while(arr[index]>arr[(index-1)/2]){
           swap(arr,index,(index-1)/2);
           index=(index-1)/2;
       }
   }

   //一个值变小往下沉的过程
   public static void heapify(int[] arr,int index,int size){
       int left=index*2+1;
       while(left<size){
           int largest = left + 1 < size && arr[left+1] > arr[left] ? left+1 : left;
           largest = arr[largest] > arr[index] ? largest :index;
           if(largest==index){
               break;
           }
           swap(arr,largest,index);
           index=largest;
           left=index*2 +1;

       }
   }

   //交换函数
   public static void swap(int[] arr, int i, int j){
       int tmp;
       tmp=arr[i];
       arr[i]=arr[j];
       arr[j]=tmp;
   }

（5）优先队列

• 优先队列不再遵循先入先出的原则，而是分为两种情况：

• 最大优先队列，无论入队顺序，当前最大的元素优先出队；

• 最小优先队列，无论入队顺序，当前最小的元素优先出队；

• 优先级队列，也叫二叉堆、堆（不要和内存中的堆区搞混了，一个是内存区域，一个是数据结构）。
  ​堆的本质上是一种完全二叉树，分为：

• 小根堆：树中每个非叶子结点都不大于其左右孩子结点的值，也就是根节点最小的堆，图a

• 大根堆：树中每个非叶子结点都不小于其左右孩子结点的值，也就是根节点最大的堆，图b

  

     public int[] MySort (int[] arr) {
         PriorityQueue<Integer> queue=new PriorityQueue<>(new Comparator<Integer>(){
             public int compare(Integer a,Integer b){
                 return a.compareTo(b);
             }
         });
       
         for(int i=0;i<arr.length;i++){
             queue.offer(arr[i]);
         }
         int[] newarr=new int[arr.length];
         for(int i=0;i<arr.length;i++){
             newarr[i]=queue.poll();
         }
         return newarr;
     }
  

设计LRU缓存结构

（1）解法1

import java.util.*;

public class Solution {
    private Map<Integer, Node> map = new HashMap<>();
    private Node head = new Node(-1,-1);
    private Node tail = new Node(-1,-1);
    private int k;
    public int[] LRU (int[][] operators, int k) {
        this.k = k;
        head.next = tail;
        tail.prev = head;
        int len = (int)Arrays.stream(operators).filter(x -> x[0] == 2).count();
        int[] res = new int[len];
        for(int i = 0, j = 0; i < operators.length; i++) {
            if(operators[i][0] == 1) {
                set(operators[i][1], operators[i][2]);
            } else {
                res[j++] = get(operators[i][1]);
            }
        }
        return res;
    }

    private void set(int key, int val) {
        if(get(key) > -1) {
            map.get(k).val = val;
        } else {
            if(map.size() == k) {
                int rk = tail.prev.key;
                tail.prev.prev.next = tail;
                tail.prev = tail.prev.prev;
                map.remove(rk);
            }
            Node node = new Node(key, val);
            map.put(key, node);
            moveToHead(node);
        }
    }

    private int get(int key) {
        if(map.containsKey(key)) {
            Node node = map.get(key);
            node.prev.next = node.next;
            node.next.prev = node.prev;
            moveToHead(node);
            return node.val;
        }
        return -1;
    }

    private void moveToHead(Node node) {
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
        node.prev = head;
    }

    static class Node{
        int key, val;
        Node prev, next;
        public Node(int key, int val) {
            this.key = key;
            this.val = val;
        }
    }
}

（2）解法2

import java.util.*;


public class Solution {
    /**
     * lru design
     * @param operators int整型二维数组 the ops
     * @param k int整型 the k
     * @return int整型一维数组
     */
    public int[] LRU (int[][] operators, int k) {
        // write code here
        ArrayList<Integer> list = new ArrayList<>();
        LRUCache lru = new LRUCache(k);
        for(int[] opt:operators){
            if(opt[0] == 1){
                lru.put(opt[1],opt[2]);
            }else{
                list.add(lru.get(opt[1]));
            }
        }
        int[] res = new int[list.size()];
        int i = 0;
        for(int val:list){
            res[i] = list.get(i);
            i++;
        }
        return res;
    }
}

//设置LRU缓存结构
class LRUCache{
    int cap;
    LinkedHashMap<Integer, Integer> cache = new LinkedHashMap<>();
    
    public LRUCache(int capactity){
        this.cap = capactity;
    }
    
    // 将key变为最近使用
    private void makeRecently(int key){
        int val = cache.get(key);
        //删除key，重新插入到队尾
        cache.remove(key);
        cache.put(key, val);
    }
    
    
    //获取值
    public int get(int key){
        if(!cache.containsKey(key)){
            return -1;
        }
        //将这个key变为最近使用的
        makeRecently(key);
        return cache.get(key);
    }
    
    //存进值
    public void put(int key,int val){
        if(cache.containsKey(key)){
            cache.put(key, val);
            //设置为最近使用
            makeRecently(key);
            return;
        }
        
        //超出缓存的大小
        if(cache.size() >= this.cap){
            //拿到链表头部的key（其最久未使用的key）
            int oldstKet = cache.keySet().iterator().next();
            cache.remove(oldstKet);
        }
        //将新的key添加到链表尾部
        cache.put(key,val);
    }
}

实现二叉树先序-中序和后序遍历

（1）递归解法

public void preorder(TreeNode root, List<Integer> list) {
    if (root != null) {
        list.add(root.val);
        preorder(root.left, list);
        preorder(root.right, list);
    }
}
public void inorder(TreeNode root, List<Integer> list) {
    if (root != null) {
        inorder(root.left, list);
        list.add(root.val);
        inorder(root.right, list);
    }
}
public void postorder(TreeNode root, List<Integer> list) {
    if (root != null) {
        postorder(root.left, list);
        postorder(root.right, list);
        list.add(root.val);
    }
}

（2）迭代解法

1） 前序遍历迭代

• 算法1
  • 1.根节点入栈
  • 2.当栈非空时，栈顶出栈，把出栈的节点值添加到 list 结尾，然后依次再入栈其右子节点和左子节点
  • ps：因为前序遍历要左子节点在右子节点前面，所以先入栈右子节点，后入栈左子节点
• 算法2
  • 1.辅助变量 curr 初始化为根节点
  • 2.当 curr != null 时，就保存这个节点值到 list 中，然后将其入栈并置 curr 为它自己的左子节点
  • 3.当 curr == null 时，说明已经遍历到二叉树的左下节点了，这时前序遍历应该遍历右子树了，首先 pop 出已经遍历保存过的父节点，然后置 curr 为 pop 出的父节点的右子节点
• 算法3
  • 和算法2的区别：父节点遍历到之后直接保存下来不再入栈，随后入栈其右子节点，这样出栈的时候也不必再置为其右子节点

    public void preorder(TreeNode root, ArrayList<Integer> list) {
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode curr = stack.pop();
            list.add(curr.val);
            if (curr.right != null) {
                stack.push(curr.right);
            }
            if (curr.left != null) {
                stack.push(curr.left);
            }
        }
    }
    public void preorder(TreeNode root, ArrayList<Integer> list) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode curr = root;
        while (!stack.isEmpty() || curr != null) {
            if (curr != null) {
                list.add(curr.val);
                stack.push(curr);
                curr = curr.left;
            } else {
                curr = stack.pop();
                curr = curr.right;
            }
        }
    }
    public void preorder(TreeNode root, ArrayList<Integer> list) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode curr = root;
        while (!stack.isEmpty() || curr != null) {
            if (curr != null) {
                list.add(curr.val);
                if (curr.right != null) {
                    stack.push(curr.right);
                }
                curr = curr.left;
            } else {
                curr = stack.pop();
            }
        }
    }

2）中序遍历迭代

• 算法1
  • 1.辅助变量 curr 初始化 root
  • 3.当栈非空或 curr 非 null 时，循环
    • 3.1 curr != null 时，说明还有左子节点存在，将 curr 入栈，并且将 curr 置为它自己的左子节点（和前序遍历的区别在于这里遍历到先不保存到 list 中，出栈的时候再将其保存到 list 中）
    • 3.2 curr == null 时，说明到二叉树左下的节点了，这时栈顶的父节点出栈赋值给 curr ，并保存节点值到 list ，将 curr 置为栈顶节点的右子节点继续循环
• 算法2
  • 算法1的另一种形式

    public void inorder(TreeNode root, ArrayList<Integer> list) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode curr = root;
        while (!stack.isEmpty() || curr != null) {
            if (curr != null) {
                stack.push(curr);
                curr = curr.left;
            } else {
                curr = stack.pop();
                list.add(curr.val);
                curr = curr.right;
            }
        }
    }

    public void inorder(TreeNode root, ArrayList<Integer> list) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode curr = root;
        while (!stack.isEmpty() || curr != null) {
            while (curr != null) {
                stack.push(curr);
                curr = curr.left;
            } 
            curr = stack.pop();
            list.add(curr.val);
            curr = curr.right;
        }
    }

3） 后序遍历迭代

• 三种算法分别对应前序遍历的反操作：
  • 前序遍历从尾部添加元素，后序遍历从头部添加元素
  • 前序遍历去左子树，后序遍历去右子树

    public void postorder(TreeNode root, ArrayList<Integer> list) {
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode curr = stack.pop();
            list.add(0, curr.val);
            if(curr.left != null) {
              stack.push(curr.left);
            }
            if(curr.right != null) {
               stack.push(curr.right); 
            }
        }
    }
    public void postorder(TreeNode root, List<Integer> list) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode curr = root;
        while (!stack.isEmpty() || curr != null) {
            if (curr != null) {
                stack.push(curr);
                list.add(0, curr.val);
                curr = curr.right;
            } else {
                curr = stack.pop();
                curr = curr.left;
            }
        }
    }
    public void postorder(TreeNode root, List<Integer> list) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode curr = root;
        while (!stack.isEmpty() || curr != null) {
            if (curr != null) {
                list.add(0, curr.val);
                if (curr.left != null) {
                    stack.push(curr.left);
                }
                curr = curr.right;
            } else {
                curr = stack.pop();
            }
        }
    }

求二叉树的层序遍历


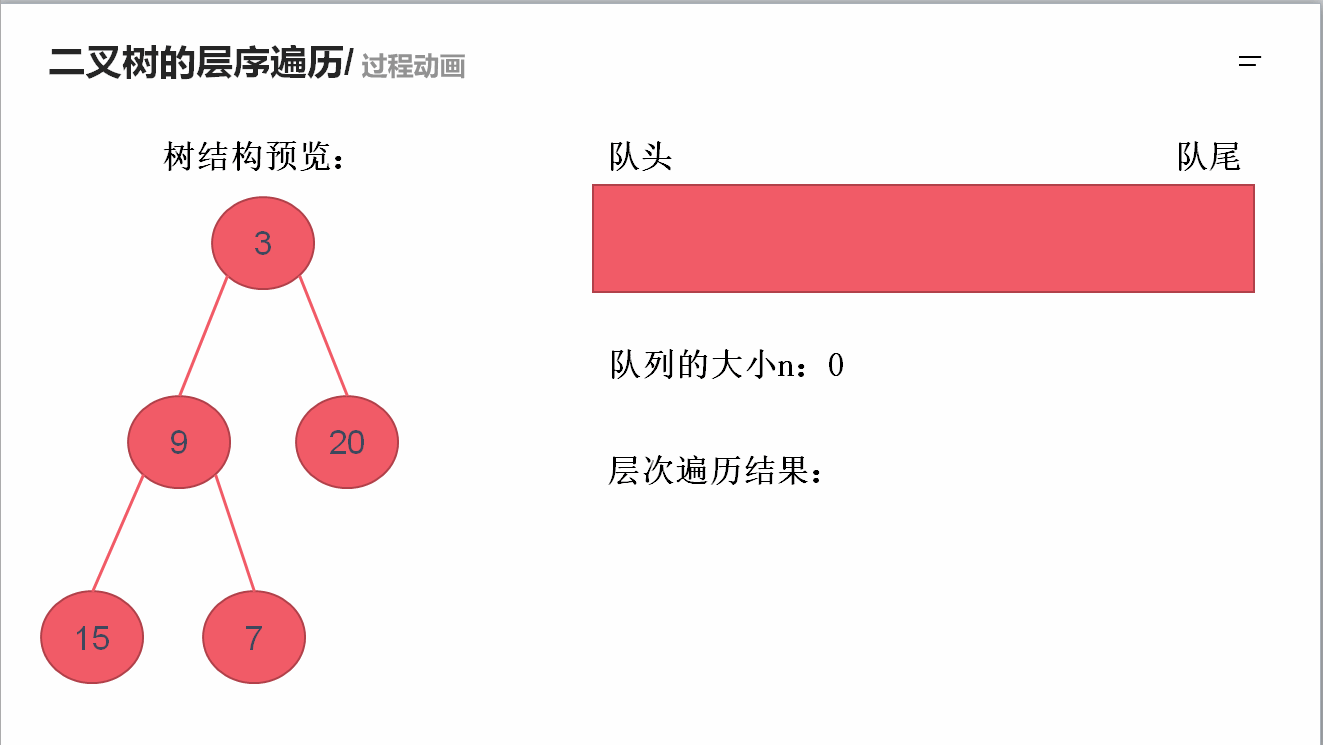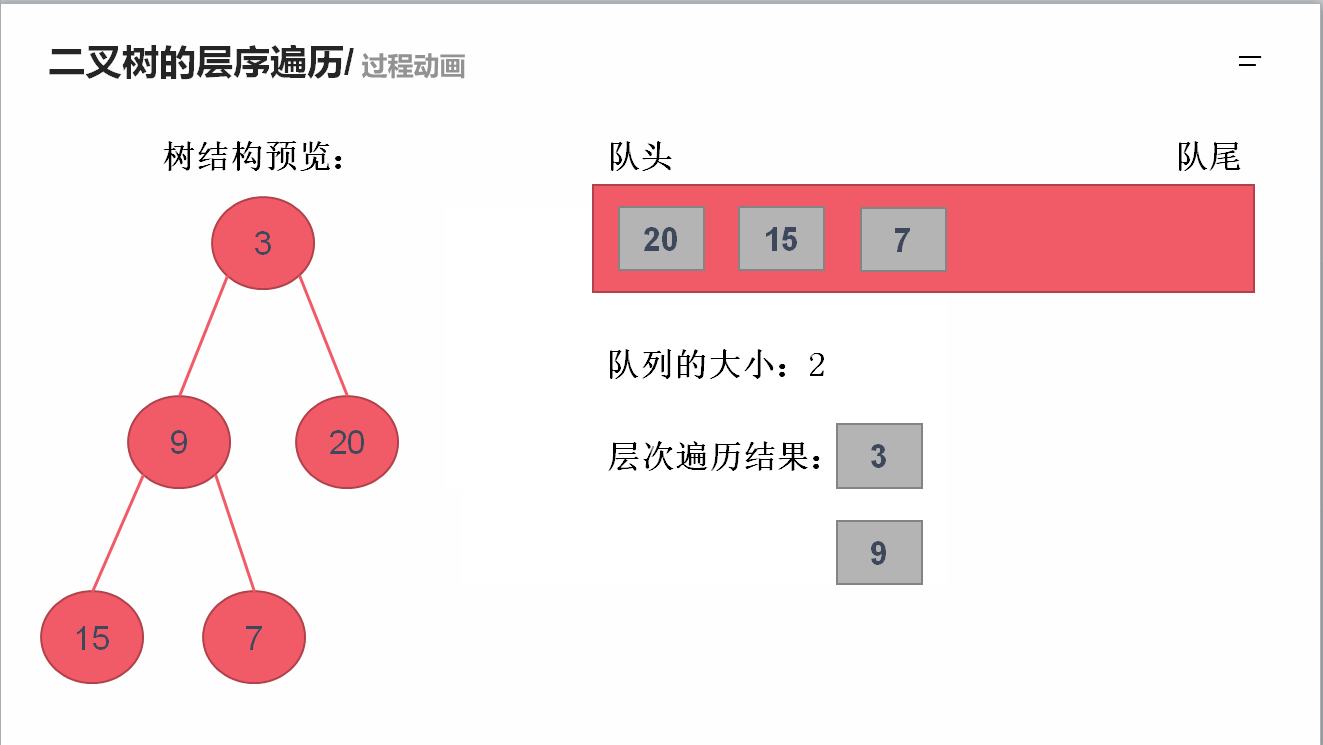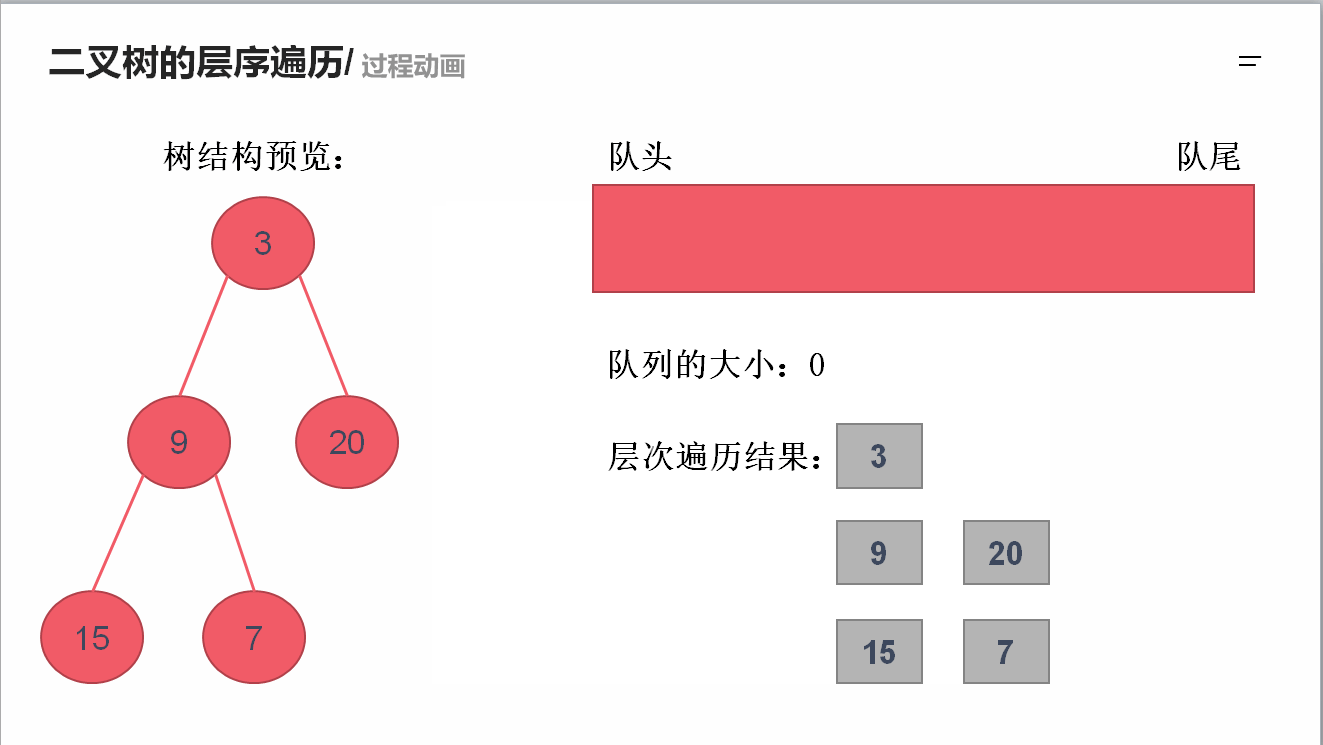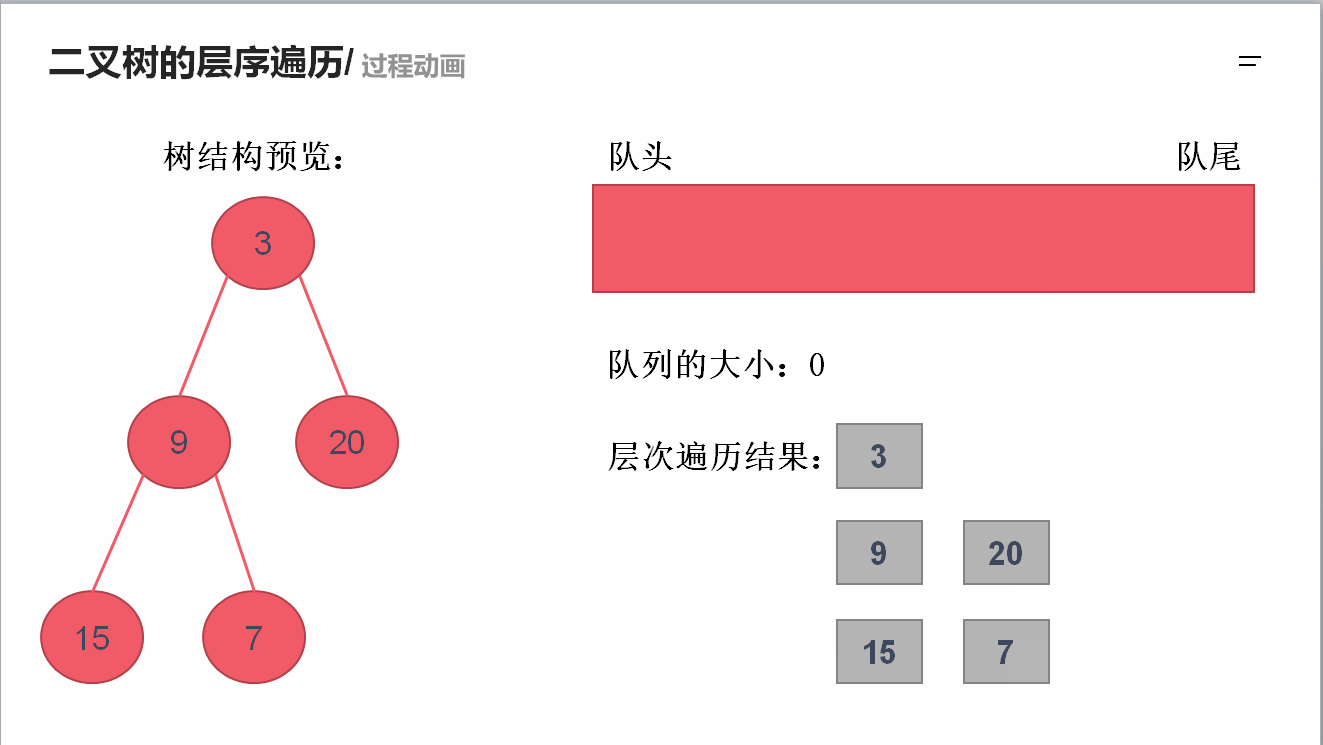需要借助队列的先进先出特性来实现

java Queue中 remove/poll, add/offer, element/peek区别

offer，add区别：

一些队列有大小限制，因此如果想在一个满的队列中加入一个新项，多出的项就会被拒绝。

这时新的 offer 方法就可以起作用了。它不是对调用 add() 方法抛出一个 unchecked 异常，而只是得到由 offer() 返回的 false。

poll，remove区别：

remove() 和 poll() 方法都是从队列中删除第一个元素。remove() 的行为与 Collection 接口的版本相似，

但是新的 poll() 方法在用空集合调用时不是抛出异常，只是返回 null。因此新的方法更适合容易出现异常条件的情况。

peek，element区别：

element() 和 peek() 用于在队列的头部查询元素。与 remove() 方法类似，在队列为空时， element() 抛出一个异常，而 peek() 返回 null

（1）队列解法:

import java.util.Queue;
import java.util.LinkedList;
import java.util.ArrayList;
public class Solution {
    public ArrayList<ArrayList<Integer>> levelOrder(TreeNode root) {
        ArrayList<ArrayList<Integer>> result = new ArrayList<ArrayList<Integer>>();
        if(root != null){
            Queue<TreeNode> queue = new LinkedList<>();
            queue.offer(root);
            while(!queue.isEmpty()){
                int size = queue.size();
                ArrayList<Integer> newLevel = new ArrayList<Integer>();
                for(int i=0; i<size; i++){
                    TreeNode temp = queue.poll();
                    newLevel.add(temp.val);
                    if(temp.left != null)
                        queue.offer(temp.left);
                    if(temp.right != null)
                        queue.offer(temp.right);
                }
                result.add(newLevel);
            }
        }
        return result;
    }
}

（2）递归解法:

public class Solution {
    private ArrayList<ArrayList<Integer>> result = new ArrayList<ArrayList<Integer>>();
    
    public ArrayList<ArrayList<Integer>> levelOrder (TreeNode root) {
        order(root, 0);
        return result;
    }
    private void order(TreeNode root, int level) {
        if (root == null) return;
        if (result.size() <= level) // 用level来判断
            result.add(new ArrayList<Integer>());
        result.get(level).add(root.val);
        order(root.left, level+1);
        order(root.right, level+1);
    }
}

最小的K个数

对于n个整数中最小的K个数的查找，可以使用各种排序算法：冒泡/堆排/快排/希尔排序等等。将此n个整数从小到大排序之后，前k个数就是所求的结果。
但是当原数组中的数据顺序不可修改，并且n的值过于大的时候，各种排序算法要将n个数加载到内存中，即：如果是海量数据中查找出最小的k个数，那么这种办法是效率很低的。

接下来介绍另外一种算法：

创建一个大小为k的数组，遍历n个整数，如果遍历到的数小于大小为k数组的最大值，则将此数与其最大值替换。
由于每次都要拿n个整数和数组中的最大值比较，所以选择大根堆这一数据结构(大家要分清楚大根堆这一数据结构和堆排序之间的区别：堆排序是在大根堆这一数据结构上进行排序的一种排序算法，一个是数据结构，一个是算法)

（1）解法一：普通排序

直接排序，然后去前k小数据。

• 快速排序

  import java.util.*;
  
  public class Solution {
      public ArrayList<Integer> GetLeastNumbers_Solution(int[] input, int k) {
          ArrayList<Integer> ans = new ArrayList<>();
          if(input == null || input.length == 0 || k == 0) {
              return ans;
          }
          partition(0, input.length-1, input, k);
          for(int i = 0; i < k; i++) {
              ans.add(input[i]);
          }
          return ans;
      }
      
      public void partition(int left, int right, int[] nums, int k) {
          if(left >= right) {
              return;
          }
          int pivot = nums[left];
          int i = left, j = right;
          while(i < j) {
              while(i < j && nums[j] > pivot) {
                  j--;
              }
              if(i < j) {
                  nums[i] = nums[j];
                  i++;
              }
              while(i < j && nums[i] < pivot) {
                  i++;
              }
              if(i < j) {
                  nums[j] = nums[i];
                  j--;
              }
          }
          nums[i] = pivot;
          if(i == k) {
              return;
          } else if(i > k) {
              partition(left, i-1, nums, k);
          } else {
              partition(i+1, right, nums, k);
          }
      }
  }
  

• 归并排序

（2）解法二：堆排序

建立一个容量为k的大根堆的优先队列。遍历一遍元素，如果队列大小

• public class Solution {
       public ArrayList<Integer> GetLeastNumbers_Solution(int [] input, int k) {
          if(input == null || input.length==0 || k>input.length) return new ArrayList();
          ArrayList<Integer> result = new ArrayList<>();
          heapSort(input);
          for(int i=0;i<k;i++){
              result.add(input[i]);
          }
          return result;
      }
       
      //堆排序
      public void heapSort(int arr[]){
          int temp;
          for(int i = arr.length/2 -1;i>=0;i--){
              adjustHeap(arr,i,arr.length);
          }
           
          for(int j=arr.length-1;j>0;j--){
              temp = arr[j];
              arr[j] = arr[0];
              arr[0] = temp;
               
              //调整对堆结构
              adjustHeap(arr,0,j);
          }
      }
       
      //调整当前以 i 索引处为堆的结构
      public void adjustHeap(int[] arr,int i,int length){
          //首先将 当前堆顶元素 arr[i] 保存起来
          int temp = arr[i];
           
          //接下来的循环就是在当前整个堆中不断地循环，找到堆中的最大值
          for(int k = i*2+1;k<length;k = k*2+1){
              // k =  i*2+1,就是当前堆的左子节点的索引，
              // 那么 k+1，代表的就是右子节点的索引
              // 在数组界限内 判断 当前堆顶节点的左右节点哪个大
              if(k+1<length && arr[k]<arr[k+1]){
                  //如果左子节点小于右子节点，我们将k指向右子节点的索引
                  k += 1;
                  // 此时 k 指向的位置就是当前堆下 值最大的位置
              }
              //判断arr[k]和堆顶顶元素的关系
              if(arr[k] > temp){
                  //我们将较大值 赋给堆顶
                  arr[i] = arr[k];
                  //接着再以k处为堆顶，继续向下循环遍历
                  i = k;
              }else{
                  break;
              }
          }
          //将最初保存的堆顶元素赋值给“最终替换了”它的那个元素的索引上
          //相当于就是将堆顶元素向下沉，所能沉到的最低位置就是 当前的 i
          arr[i] = temp;
      }
  }
  

• public class Solution {
      public ArrayList<Integer> GetLeastNumbers_Solution(int [] input, int k) {
          ArrayList<Integer> list = new ArrayList<>();
          if (input == null || input.length == 0 || k > input.length || k == 0)
              return list;
          int[] arr = new int[k + 1];//数组下标0的位置作为哨兵，不存储数据
          //初始化数组
          for (int i = 1; i < k + 1; i++)
              arr[i] = input[i - 1];
          buildMaxHeap(arr, k + 1);//构造大根堆
          for (int i = k; i < input.length; i++) {
              if (input[i] < arr[1]) {
                  arr[1] = input[i];
                  adjustDown(arr, 1, k + 1);//将改变了根节点的二叉树继续调整为大根堆
              }
          }
          for (int i = 1; i < arr.length; i++) {
              list.add(arr[i]);
          }
          return list;
      }
       /**
       * @Author: ZwZ
       * @Description: 构造大根堆 
       * @Param: [arr, length]  length:数组长度 作为是否跳出循环的条件
       */
      public void buildMaxHeap(int[] arr, int length) {
          if (arr == null || arr.length == 0 || arr.length == 1)
              return;
          for (int i = (length - 1) / 2; i > 0; i--) {
              adjustDown(arr, i, arr.length);
          }
      }
      /**
       * @Author: ZwZ
       * @Description: 堆排序中对一个子二叉树进行堆排序 
       * @Param: [arr, k, length] 
       */
      public void adjustDown(int[] arr, int k, int length) {
          arr[0] = arr[k];//哨兵
          for (int i = 2 * k; i <= length; i *= 2) {
              if (i < length - 1 && arr[i] < arr[i + 1])
                  i++;//取k较大的子结点的下标
              if (i > length - 1 || arr[0] >= arr[i])
                  break;
              else {
                  arr[k] = arr[i];
                  k = i; //向下筛选
              }
          }
          arr[k] = arr[0];
      }
  }
  

（3）解法三：快排思想

对数组[l, r]一次快排partition过程可得到，[l, p), p, [p+1, r)三个区间,[l,p)为小于等于p的值
[p+1,r)为大于等于p的值。
然后再判断p，利用二分法

1. 如果[l,p), p，也就是p+1个元素（因为下标从0开始），如果p+1 == k, 找到答案

2. 如果p+1 < k, 说明答案在[p+1, r)区间内，

3. 如果p+1 > k , 说明答案在[l, p)内

   写法1:

public class Solution {
    ArrayList<Integer> result = new ArrayList<>();
  
    public ArrayList<Integer> GetLeastNumbers_Solution(int [] input, int k) {
        if(k == 0 || k >input.length) {
            return result;
        }
        quickSearch(input, 0, input.length - 1, k - 1);
        return result;
    }

    void quickSearch(int[] nums, int left, int right, int k) {
        int index = partition(nums, left, right);
        if (index == k) {
            for (int i = 0; i <=k; i++) {
                result.add(nums[i]);
            }
        }else if (index > k) {
            quickSearch(nums, left, index - 1, k);
        } else {
            quickSearch(nums, index + 1, right, k);
        }
    }

    int partition(int[]nums, int left, int right) {
        int value = nums[left];
        int index = left;
        for (int i = left; i <= right; i++) {
            if (nums[i] < value) {
                index++;
                swap(nums, i, index);
            }
        }
        swap(nums, index, left);
        return index;
    }

    void swap(int[] nums, int left, int right) {
        int temp = nums[left];
        nums[left] = nums[right];
        nums[right] = temp;
    }
}

写法2：

public class Solution {
    public ArrayList<Integer> GetLeastNumbers_Solution(int[] input, int k) {
        ArrayList<Integer> ans = new ArrayList<>();
        if(input == null || input.length == 0 || k == 0) {
            return ans;
        }
        partition(0, input.length-1, input, k);
        for(int i = 0; i < k; i++) {
            ans.add(input[i]);
        }
        return ans;
    }
    
    public void partition(int left, int right, int[] nums, int k) {
        if(left >= right) {
            return;
        }
        int pivot = nums[left];
        int i = left, j = right;
        while(i < j) {
            while(i < j && nums[j] > pivot) {
                j--;
            }
            if(i < j) {
                nums[i] = nums[j];
                i++;
            }
            while(i < j && nums[i] < pivot) {
                i++;
            }
            if(i < j) {
                nums[j] = nums[i];
                j--;
            }
        }
        nums[i] = pivot;
        if(i == k) {
            return;
        } else if(i > k) {
            partition(left, i-1, nums, k);
        } else {
            partition(i+1, right, nums, k);
        }
    }
}

（4）解法四：大顶堆

输入n个整数，找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4。
维护一个大小为 K 的最小堆过程如下：使用大顶堆。在添加一个元素之后，如果大顶堆的大小大于 K，
那么将大顶堆的堆顶元素去除，也就是将当前堆中值最大的元素去除，从而使得留在堆中的元素都比被去除的元素来得小。
应该使用大顶堆来维护最小堆，而不能直接创建一个小顶堆并设置一个大小，企图让小顶堆中的元素都是最小元素
Java 的 PriorityQueue 实现了堆的能力，PriorityQueue 默认是小顶堆，
可以在在初始化时使用 Lambda 表达式 (o1, o2) -> o2 - o1 来实现大顶堆。

public class GetLeastNumbers_Solution {
    public ArrayList<Integer> GetLeastNumbers_Solution(int [] nums,int k){
        if (k > nums.length || k <0)return new ArrayList<>();
        PriorityQueue<Integer> maxHeap = new PriorityQueue<>(((o1, o2) -> o2-o1));
        for (int i = 0; i <nums.length ; i++) {
            maxHeap.add(nums[i]);
            if (maxHeap.size() >k){
                maxHeap.poll();
            }
        }
        return new ArrayList<>(maxHeap);
    }
}

寻找第K大

（1）快排：

import java.util.*;

public class Solution {
    public int findKth(int[] a, int n, int K) {
        // write code here
        return findK(a, 0, n-1, K);
    }

    public static int partition(int[] arr, int left, int right) {
        int pivot = arr[left];

        while (left < right) {
            while (left < right && arr[right] <= pivot) {
                right--;
            }
            arr[left] = arr[right];
            while (left < right && arr[left] >= pivot) {
                left++;
            }
            arr[right] = arr[left];
        }
        arr[left] = pivot;
        return left;
    }

    public static int findK(int[] arr, int left, int right, int k) {
        if (left <= right) {
            int pivot = partition(arr, left, right);

            if (pivot == k - 1) {
                return arr[pivot];
            } else if (pivot < k - 1) {
                return findK(arr, pivot + 1, right, k);
            } else {
                return findK(arr, left, pivot - 1, k);
            }
        }
        return -1;
    }
}

（2）小顶堆：

public class Solution {
    public int findKth(int[] a, int n, int K) {
        // write code here
        PriorityQueue<Integer> queue = new PriorityQueue<>(K,new Comparator<Integer>(){
            @Override
            public int compare(Integer o1 , Integer o2){ //初始化一个小顶堆
                return o1.compareTo(o2);
            }
        });
 
        for (int ele : a){
            if (queue.size() < K || ele > queue.peek()) 
              	queue.offer(ele);
            while (queue.size() > K) 
              	queue.poll();
        }
        return queue.peek();
    }
}

两数之和

（1）解法1:

public class Solution {
    /**
     * 
     * @param numbers int整型一维数组 
     * @param target int整型 
     * @return int整型一维数组
     */
    public int[] twoSum (int[] numbers, int target) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int cur = 0, tmp; cur < numbers.length; cur++){
            tmp = numbers[cur];
            if (map.containsKey(target - tmp)){
                return new int[] {map.get(target - tmp) + 1, cur + 1};
            }
            map.put(tmp, cur);
        }
        throw new RuntimeException("results not exits");
    }
}

（2）解法2:

public class Solution {
    /**
     * 
     * @param numbers int整型一维数组 
     * @param target int整型 
     * @return int整型一维数组
     */
    public int[] twoSum (int[] numbers, int target) {
        // write code here
        HashMap<Integer, Integer> map = new HashMap<>();
        int index1 = -1;
        int index2 = -1;
        for (int i = 0; i < numbers.length; i++) {
            if (map.containsKey(target - numbers[i])) {
                index1 = map.get(target - numbers[i]);
                index2 = i + 1;
                break;
            } else {
                map.put(numbers[i], i + 1);
            }
        }
        return new int[]{index1, index2};
    }
}

（3）解法3:

public class Solution {
    /**
     * 
     * @param numbers int整型一维数组 
     * @param target int整型 
     * @return int整型一维数组
     */
    public int[] twoSum (int[] numbers, int target) {
        Map<Integer, Integer> map = new HashMap<>();
        for(int i = 0; i < numbers.length; i ++){
            map.put(numbers[i], i);
        }
        
        for(int i = 0; i < numbers.length; i ++){
            int num = target - numbers[i];
            Integer numIndex = map.get(num);
            if(numIndex != null && numIndex != i ){
                return new int[]{i+1, numIndex+1};
            }
        }
        return new int[]{-1,-1};
    }
}

合并两个排序的链表

（1）迭代：

public class Solution {
    public ListNode Merge(ListNode list1,ListNode list2) {

        ListNode head = new ListNode(Integer.MIN_VALUE);
        ListNode cur = head;

        while (list1!=null && list2!=null) {
            if (list1.val <list2.val) {
                cur.next = list1;
                cur = cur.next;
                list1 = list1.next;
            } else {
                cur.next = list2;
                cur = cur.next;
                list2 = list2.next;
            }
        }

        if (list1 == null) {
            cur.next = list2;
        } else {
            cur.next = list1;
        }

        return head.next;
    }
}

（2）递归：

/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode Merge(ListNode list1,ListNode list2) {
        if(list1 == null) return list2;
        if(list2 == null) return list1;
        if(list1.val > list2.val){
            list2.next = Merge(list1,list2.next);
            return list2;
        }else{
            list1.next = Merge(list1.next,list2);
            return list1;
        }
    }
}

合并k个已排序的链表

import java.util.ArrayList;
public class Solution {
    //两个链表合并函数
    public ListNode Merge(ListNode list1, ListNode list2) { 
        //一个已经为空了，直接返回另一个
        if(list1 == null) 
            return list2;
        if(list2 == null)
            return list1;
        //加一个表头
        ListNode head = new ListNode(0); 
        ListNode cur = head;
        //两个链表都要不为空
        while(list1 != null && list2 != null){ 
            //取较小值的节点
            if(list1.val <= list2.val){ 
                cur.next = list1;
                //只移动取值的指针
                list1 = list1.next; 
            }else{
                cur.next = list2;
                //只移动取值的指针
                list2 = list2.next; 
            }
            //指针后移
            cur = cur.next; 
        }
        //哪个链表还有剩，直接连在后面
        if(list1 != null) 
            cur.next = list1;
        else
            cur.next = list2;
        //返回值去掉表头
        return head.next; 
    }
    
    //划分合并区间函数
    ListNode divideMerge(ArrayList<ListNode> lists, int left, int right){ 
        if(left > right)  return null;
        
        //中间一个的情况
        if(left == right)  return lists.get(left);
        
        //从中间分成两段，再将合并好的两段合并
        int mid = (left + right) / 2; 
        return Merge(divideMerge(lists, left, mid), divideMerge(lists, mid + 1, right));
    }
    
    public ListNode mergeKLists(ArrayList<ListNode> lists) {
        //k个链表归并排序
        return divideMerge(lists, 0, lists.size() - 1);
    }
}

用两个栈实现队列

（1）解法1:

public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();
     
    public void push(int node) {
        stack1.push(node);
    }
     
    public int pop() {
        if(stack2.isEmpty()){
            while(!stack1.isEmpty()){
                stack2.push(stack1.pop());
            }
        }
        return stack2.pop();
    }
}

（2）解法2:

public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();

    public void push(int node) {
        while(!stack2.isEmpty()) {
            stack1.push(stack2.pop());
        }
        stack2.push(node);
        while(!stack1.isEmpty()) {
            stack2.push(stack1.pop());
        }
    }

    public int pop() {
        return stack2.pop();
    }
}

跳台阶

对于本题,前提只有 一次 1阶或者2阶的跳法。

a.如果两种跳法，1阶或者2阶，那么假定第一次跳的是一阶，那么剩下的是n-1个台阶，跳法是f(n-1);

b.假定第一次跳的是2阶，那么剩下的是n-2个台阶，跳法是f(n-2)

c.由a\b假设可以得出总跳法为: f(n) = f(n-1) + f(n-2)

d.然后通过实际的情况可以得出：只有一阶的时候 f(1) = 1 ,只有两阶的时候可以有 f(2) = 2

e.可以发现最终得出的是一个斐波那契数列：

​ | 1, (n=1)

f(n) = | 2, (n=2)

​ | f(n-1)+f(n-2) ,(n>2,n为整数)

（1）递归

public class Solution {
    public int jumpFloor(int target) {
        if (target <= 0) {return -1;} 
      	if (target == 1) { return 1;}
      	if (target ==2)  { return 2;} 
        return  jumpFloor(target-1)+jumpFloor(target-2);
    }
}

（2）迭代解法1

public class Solution {
    public int jumpFloor(int target) {
        // 状态转移方程 dp(n) = dp(n-1) + dp(n-2)
        // 初始值dp(0) = 1  dp(1) = 1
        // 验证 dp(2) = dp(1) + dp(0） = 2
        if (target <= 1) return 1;
        int[] dp = new int[target+1];
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <= target; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[target];
    }
}

（3）迭代解法2:

自底向上型循环求解，时间复杂度为 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HGnndKNE-1629356069694)(https://www.nowcoder.com/equation?tex=O(n)]&preview=true)

public class Solution {
    public int JumpFloor(int target) {
        // f[1] = 1, f[0] = 1 (f[0]是为了简便作答自己添加的)
        int a = 1, b = 1;
        for (int i = 2; i <= target; i++) {
            // 求f[i] = f[i - 1] + f[i - 2]
            a = a + b; // 这里求得的 f[i] 可以用于下次循环求 f[i+1]
            // f[i - 1] = f[i] - f[i - 2]
            b = a - b; // 这里求得的 f[i-1] 可以用于下次循环求 f[i+1]
        }
        return a;
    }
}

自底向上求递推式的过程，该方法二原始的版本为：

public class Solution {
    public int JumpFloor(int target) {
        if (target <= 1) {
            return 1;
        }
        // a 表示第 f[i-2] 项，b 表示第 f[i-1] 项
        int a = 1, b = 1, c = 0;
        for (int i = 2; i <= target; i++) {
            c = a + b; // f[i] = f[i - 1] + f[i - 2];
            // 为下一次循环求 f[i + 1] 做准备
            a = b; // f[i - 2] = f[i - 1]
            b = c; // f[i - 1] = f[i]
        }
        return c;
    }
}

子数组的最大累加和问题

（1）动态规划

  public int maxsumofSubarray (int[] arr) {
        //1.dp状态设置： dp[i]就是以nums[i]为结尾的的连续子数组的最大和
        int[] dp = new int[arr.length];
        //2.初态设置：dp[0]必须包含nums[0] 所以：
        dp[0] = arr[0];
        int max = dp[0];
        //3.转移方程：
        //因为nums[i]无论如何都要包括 那么可以选择的余地就是dp[i-1]了
        //dp[i-1]<0 那么不如只选nums[i]了 dp[i-1]>0 那就nums[i]带上dp[i-1]
        for (int i = 1; i < arr.length; i++) {
            dp[i] =  dp[i-1]>0?dp[i-1]+arr[i]:arr[i];
            //由于无论如何都要包括nums[i] 那么如果最后的nums[len-1]<0
            //那么此时dp[len-1]肯定不是最大连续和 需要max筛选
            max = Math.max(max,dp[i]);
        }
    return max;
}

（2）迭代

public int maxsumofSubarray (int[] arr) {
  	if(arr.length == 0)  return 0;
    int maxSum = 0;
    int sum = 0;
    for(int i = 0; i < arr.length; i++){
      sum = sum + arr[i] > 0 ? sum + arr[i] : 0;
      maxSum = maxSum > sum ? maxSum : sum;
    }
    return maxSum;
}

链表中的节点每k个一组翻转

（1）链表头插法

import java.util.*;
public class Solution {
    public ListNode reverseKGroup (ListNode head, int k) {
        if(head==null||head.next==null||k==1) return head;
        ListNode res = new ListNode(0);
        res.next = head;
        int length = 0;
        ListNode pre = res,
                 cur = head,
                 temp = null;
        while(head!=null){
            length++;
            head = head.next;
        }
        //分段使用头插法将链表反序
        for(int i=0; i<length/k; i++){
            //pre作为每一小段链表的头节点，负责衔接
            for(int j=1; j<k; j++){
                temp = cur.next;
                cur.next = temp.next;
                //相当于头插法，注意：
                //temp.next = cur是错误的，temp需要连接的不是前一节点，而是子序列的头节点
                temp.next = pre.next;
                pre.next = temp;
            }
            //每个子序列反序完成后，pre，cur需要更新至下一子序列的头部
            pre = cur;
            cur = cur.next;
        }
        return res.next;
    }
}

（2）迭代法

public ListNode reverseKGroup(ListNode head, int k) {
     if (head == null || head.next == null){
         return head;
     }
     //定义一个假的节点。
     ListNode dummy=new ListNode(0);
     //假节点的next指向head。
     // dummy->1->2->3->4->5
     dummy.next=head;
     //初始化pre和end都指向dummy。pre指每次要翻转的链表的头结点的上一个节点。
     //end指每次要翻转的链表的尾节点
     ListNode pre=dummy;
     ListNode end=dummy;

     while(end.next!=null){
         //循环k次，找到需要翻转的链表的结尾,这里每次循环要判断end是否等于空
         //因为如果为空，end.next会报空指针异常。
         //dummy->1->2->3->4->5 若k为2，循环2次，end指向2
         for(int i=0;i<k&&end != null;i++){
             end=end.next;
         }
         //如果end==null，即需要翻转的链表的节点数小于k，不执行翻转。
         if(end==null){
             break;
         }
         //先记录下end.next,方便后面链接链表
         ListNode next=end.next;
         //然后断开链表
         end.next=null;
         //记录下要翻转链表的头节点
         ListNode start=pre.next;
         //翻转链表,pre.next指向翻转后的链表。1->2 变成2->1。 
         //dummy->2->1
         pre.next=reverse(start);
         //翻转后头节点变到最后。通过.next把断开的链表重新链接。
         start.next=next;
         //将pre换成下次要翻转的链表的头结点的上一个节点。即start
         pre=start;
         //翻转结束，将end置为下次要翻转的链表的头结点的上一个节点。
         //即start
         end=start;
     }
     return dummy.next;
 }

 //链表翻转
 // 例子：   head： 1->2->3->4
 public ListNode reverse(ListNode head) {
      //单链表为空或只有一个节点，直接返回原单链表
     if (head == null || head.next == null){
         return head;
     }
     //前一个节点指针
     ListNode preNode = null;
     //当前节点指针
     ListNode curNode = head;
     //下一个节点指针
     ListNode nextNode = null;
     while (curNode != null){
         nextNode = curNode.next;
         //nextNode 指向下一个节点,保存当前节点后面的链表。
         curNode.next=preNode;
         //将当前节点next域指向前一个节点   null<-1<-2<-3<-4
         preNode = curNode;
         //preNode 指针向后移动。preNode指向当前节点。
         curNode = nextNode;
         //curNode指针向后移动。下一个节点变成当前节点
     }
     return preNode;
 }

（3）递归

1、找到待翻转的k个节点（注意：若剩余数量小于 k 的话，则不需要反转，因此直接返回待翻转部分的头结点即可）。
2、对其进行翻转。并返回翻转后的头结点（注意：翻转为左闭又开区间，所以本作的尾结点其实就是下一作的头结点）。
3、对下一轮 k 个节点也进行翻转操作。
4、将上一轮翻转后的尾结点指向下一轮翻转后的头节点，即将每一轮翻转的k的节点连接起来。

写法1:

 public ListNode reverseKGroup(ListNode head, int k) {
     if (head == null || head.next == null) {
         return head;
     }
     ListNode tail = head;
     for (int i = 0; i < k; i++) {
         //剩余数量小于k的话，则不需要反转。
         if (tail == null) {
             return head;
         }
         tail = tail.next;
     }
     // 反转前 k 个元素
     ListNode newHead = reverse(head, tail);
     //下一轮的开始的地方就是tail
     head.next = reverseKGroup(tail, k);

     return newHead;
 }

 /*
 左闭又开区间
  */
 private ListNode reverse(ListNode head, ListNode tail) {
     ListNode pre = null;
     ListNode next = null;
     while (head != tail) {
         next = head.next;
         head.next = pre;
         pre = head;
         head = next;
     }
     return pre;

 }

写法2:使用栈翻转

public class Solution {
    public ListNode reverseKGroup (ListNode head, int k) {
        // write code here
        //使用一个栈来反转每段链表
        Stack<ListNode> stack = new Stack<ListNode>();
        ListNode cur = head;
        for(int i = 0;i<k;i++){
            if(cur == null){
                //如果这段链表长度不够k，则直接返回这个链表
                return head;
            }
            stack.push(cur);
            cur = cur.next;
        }
        //根据栈中的节点构造链表，构造出来的是原来链表的反转
        ListNode res = stack.pop();
        ListNode temp = res;
        while(!stack.isEmpty()){
            temp.next = stack.pop();
            temp = temp.next;
        }
        //反转后的链表的尾节点是递归返回的头节点
        temp.next = reverseKGroup(cur,k);
        return res;
    }
}

最长无重复子数组

（1）方法一：滑动窗口法

我们可以利用双指针模拟一个滑动窗口。初始化该窗口为(left, right]。所以left从-1开始。窗口不断往右扩大。因为我们要的是无重复子数组，因此，遇到有重复的数字，在窗口左侧进行缩小。
在每次滑动时，对窗口的大小进行比较，保留最大的长度。

import java.util.*;


public class Solution {
    /**
     * 
     * @param arr int整型一维数组 the array
     * @return int整型
     */
    public int maxLength (int[] arr) {
        // write code here
        if(arr.length < 2){
            return arr.length;
        }

        HashMap<Integer, Integer> windows = new HashMap<>();
        int res = 0;
        //用双指针来模拟一个滑动窗口
        int left = -1;
        //窗口向右滑动
        for(int right = 0; right < arr.length; right++){
            //遇到重复数字
            if(windows.containsKey(arr[right])){
                //因为有可能遇到的重复数字的位置 比 left还要前
                //所以不能把left置于该位置前一位， 而是比较哪个最大，目的还是为了缩小窗口
                //确保窗口内全是不重复的数字
                left = Math.max(left, windows.get(arr[right]));
            }
            //每次更新窗口大小
            res = Math.max(res, right-left);
            //将数字位置更新到windows中
            windows.put(arr[right], right);
        }
        return res;
    }
}

（2）方法二：双指针 + 回头遍历

定义双指针， right指针对数组进行遍历，left指针对arr[right]前的子数组进行遍历。当left小于0或者遇到重复数字时，终止left遍历。
定义res代表最长的长度，tmp代表当前字符拥有的子串长度。
每次更新tmp时，也得更新res。

import java.util.*;


public class Solution {
    /**
     * 
     * @param arr int整型一维数组 the array
     * @return int整型
     */
    public int maxLength (int[] arr) {
        // write code here
        int res = 0, tmp = 0;
        for(int right = 0; right < arr.length; right++){
            int left = right -1;
            //回头遍历
            while(left >= 0 && arr[right] != arr[left]){
                left --;
            }
            //若指针距离比上一个字符拥有的子串长度要大，就tmp+1 否则说明，遇到了重复数字，设置为新的指针距离，方便下一步res比较
            tmp = tmp < right - left ? tmp + 1 : right - left;
            //更新res指
            res = Math.max(res, tmp);
        }
        return res;
    }
}

判断链表中是否有环

（1）快慢指针解决

判断链表是否有环应该是老生常谈的一个话题了，最简单的一种方式就是快慢指针，慢指针针每次走一步，快指针每次走两步，如果相遇就说明有环，如果有一个为空说明没有环

public boolean hasCycle(ListNode head) {
    if (head == null)
        return false;
    //快慢两个指针
    ListNode slow = head;
    ListNode fast = head;
    while (fast != null && fast.next != null) {
        //慢指针每次走一步
        slow = slow.next;
        //快指针每次走两步
        fast = fast.next.next;
        //如果相遇，说明有环，直接返回true
        if (slow == fast)
            return true;
    }
    //否则就是没环
    return false;
}

写法2:

/**
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    /**
    判断链表是否有环，用快慢指针
    */
    public boolean hasCycle(ListNode head) {
        ListNode fast = head, slow = head;
        while(slow != null && fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            // 判断是否重合
            if(slow == fast) {
                return true;
            }
        }
        return false;
    }
}

（2）逐个删除

一个链表从头节点开始一个个删除，所谓删除就是让他的next指针指向他自己。如果没有环，从头结点一个个删除，最后肯定会删完。如果是环形的，那么有两种情况，一种是o型的，一种是6型的。

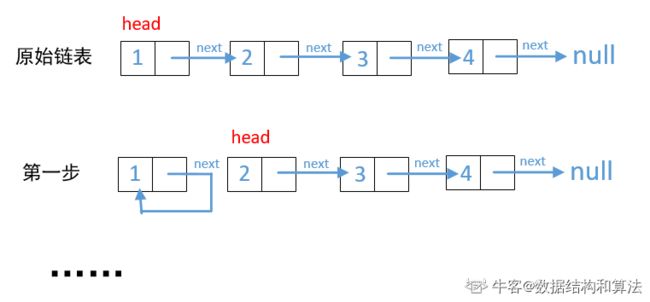
public boolean hasCycle(ListNode head) {
  //如果head为空，或者他的next指向为空，直接返回false
  if (head == null || head.next == null)
    return false;
  //如果出现head.next = head表示有环
  if (head.next == head)
    return true;
  ListNode nextNode = head.next;
  //当前节点的next指向他自己，相当于把它删除了
  head.next = head;
  //然后递归，查看下一个节点
  return hasCycle(nextNode);
}

合并两个有序的数组

（1）插入排序

public class Solution {
    public void merge(int A[], int m, int B[], int n) {
        // 插入排序
        int i=0;
        int j=0;
        while(i<m+n && j<n){
            if(A[i]>B[j]){
                // i以及i之后的往后移动
                for(int cur=m+n-1;cur>i;cur--){
                    A[cur]=A[cur-1];
                }
                A[i]=B[j];
                j++;
                i++;
            }else{i++;}
        }
        // 如果剩余的B大于A的最大值
        for(int q=j;q<n;q++){
            A[m+q]=B[q];
        }
    }
}

（2）归并排序

public class Solution {
    public void merge(int A[], int m, int B[], int n) {
        int[] result=new int[m+n];
        int t=0;
        int i=0,j=0;
        while(i<m&&j<n){
            if(A[i]<=B[j]){//两边有序数组相互比较得出小的元素依次存放
                result[t++]=A[i++];
            }else{
                result[t++]=B[j++];
            }
        }
        //将剩余元素依次存放在result数组中
        while(i<m){//左边数组A如果还有剩余元素，全部存放在result数组中
            result[t++]=A[i++];
        }
         while(j<n){//右边数组B如果还有剩余元素，全部存放在result数组中
            result[t++]=B[j++];
        }
        for(int sum=0;sum<result.length;sum++){//最后通过遍历将result数组元素存放到A数组中
            A[sum]=result[sum];
        }
    }
}

（3）双指针

/***
*整体类比ArrayList中add操作的数组移动
*比较后用System.arraycopy()函数
****/
public class Solution {
    public void merge(int A[], int m, int B[], int n) {
        int a = 0;
        int b = 0;
        while(b < n){
            if(a >= m || B[b] <= A[a]){
                System.arraycopy(A , a, A, a+1, m-a);
                m++;
                A[a++] = B[b++];
            }else{
                a++;
            }
        }
    }
}

（4）

import java.util.*;
public class Solution {
    public void merge(int A[], int m, int B[], int n) {
        for (int i = 0; i < n; i++) {
            A[m + i] = B[i];
        }
        Arrays.sort(A);
    }
}

链表中环的入口结点

(1) 指针判断

思路：1.判断链表中有环 -> 2.得到环中节点的数目 -> 3.找到环中的入口节点

/*
 public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}
*/
public class Solution {

    public ListNode EntryNodeOfLoop(ListNode pHead)
    {
        if(pHead == null){
            return null;
        }
        // 1.判断链表中有环
        ListNode l=pHead,r=pHead;
        boolean flag = false;
        while(r != null && r.next!=null){
            l=l.next;
            r=r.next.next;
            if(l==r){
                flag=true;
                break;
            }
        }
        if(!flag){
            return null;
        }else{
            // 2.得到环中节点的数目
            int n=1;
            r=r.next;
            while(l!=r){
                r=r.next;
                n++;
            }
            // 3.找到环中的入口节点
            l=r=pHead;
            for(int i=0;i<n;i++){
                r=r.next;
            }
            while(l!=r){
                l=l.next;
                r=r.next;
            }
            return l;
        }

    }
}

写法2:

public class Solution {

    public ListNode EntryNodeOfLoop(ListNode pHead) {
        if(pHead == null || pHead.next == null) {
            return null;
        }
        ListNode slow = pHead;
        ListNode fast = pHead;
        while(fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
            if(slow == fast) {
                ListNode p = pHead;
                while(p != slow) {
                    p = p.next;
                    slow = slow.next;
                }
                return p;
            }
        }
        return null;
    }
}

（2）使用集合

写法1:

public ListNode EntryNodeOfLoop(ListNode pHead) {
  //方法一：利用Map
  Map<ListNode,Integer> map = new HashMap();
  ListNode node = pHead;
  while (node != null){
    map.put(node,map.getOrDefault(node,0) + 1);
    if (map.get(node) > 1) return node;
    //或：if (map.get(node) == 2) return node; //一个意思
    node = node.next;
  }
  return null;
}

写法2:

public ListNode EntryNodeOfLoop(ListNode pHead) {
  //方法二：利用Set
  Set<ListNode> set = new HashSet();
  while(pHead != null){
    if(set.contains(pHead)) return pHead;
    else set.add(pHead);
    pHead = pHead.next;
  }
  return null;
}

括号序列

（1）压栈和取栈

'(','[','{' 这三个就压栈
')',']','}' 这三个就取栈，取栈时判断一下是不是对应的括号，如果是就取栈成功，不是就不能取。
这样最后看栈是不是为空，不为空就说明顺序不正确

public boolean isValid (String s) {
        //遇到括号匹配这样的题，首选使用栈来做
        //每次遍历遇到'('、'['和'{'时，就将其对应的方括号')'、']'和'}'放入栈中
        //然后遍历下一个，并与栈顶元素进行比较
        //如果不同直接返回false；如果相同就将栈顶的反括号弹出，遍历结束都没有返回false就说明合法，返回true
        Stack<Character> stack = new Stack<>();
        char[] temp = s.toCharArray();
        for (char c : temp){//遍历字符，如果遇到左括号，就把相应的右括号压入栈顶
            if (c == '(') stack.push(')');
            else if (c == '[') stack.push(']');
            else if (c == '{') stack.push('}');
            //else if (stack.isEmpty()) return false;//字符还没有遍历完就出现栈为空就返回false
            //else if (stack.pop() != c) return false;//如果能到达这一步，就每次从栈顶pop出一个元素与当前元素c
                                                    //进行比较，如果不同就返回false
            //也可以将上面两行代码合并：
            else if (stack.isEmpty() || stack.pop() != c) return false;
        }
        return stack.isEmpty();//遍历结束如果栈为空就返回true，否则返回false
    }

（2）字符替换

public boolean isValid (String s) {
  boolean flag = true;
  while(flag){
    int len = s.length();
    s=s.replace("()","");
    s=s.replace("[]","");
    s=s.replace("{}","");
    if(len == s.length()){
      flag=false;
    }
  }
  return s.length() == 0;
}

链表中倒数最后k个结点

(1)快慢双指针

import java.util.*;
public class Solution {
    public ListNode FindKthToTail (ListNode pHead, int k) {
        int n = 0;
        ListNode fast = pHead; 
        ListNode slow = pHead;
        //快指针先行k步
        for(int i = 0; i < k; i++){  
            if(fast != null)
                fast = fast.next;
            //达不到k步说明链表过短，没有倒数k
            else 
                return slow = null;
        }
        //快慢指针同步，快指针先到底，慢指针指向倒数第k个
        while(fast != null){ 
            fast = fast.next;
            slow = slow.next;
        }
        return slow;
    }
}

(2) 先找长度再找最后k

import java.util.*;
public class Solution {
    public ListNode FindKthToTail (ListNode pHead, int k) {
        int n = 0;
        ListNode p = pHead;
         //遍历链表，统计链表长度
        while(p != null){
            n++;
            p = p.next;
        }
        //长度过小，返回空链表
        if(n < k) 
            return null;
        p = pHead;
        //遍历n-k次
        for(int i = 0; i < n - k; i++) 
            p = p.next;
        return p;
    }
}

删除链表的倒数第n个节点

(1)先得到链表的长度，然后删除倒数第n个结点

public class Solution {
    /**
     * 
     * @param head ListNode类 
     * @param n int整型 
     * @return ListNode类
     */
    public ListNode removeNthFromEnd (ListNode head, int n) {
         ListNode cur = head;
        if (head == null || head.next == null) return null;
        List<ListNode> list = new ArrayList<>();
        while (cur != null) {
            list.add(cur);
            cur = cur.next;
        }
        list.remove(list.size() - n);
        ListNode resNode = list.get(0);
        ListNode temp = resNode;
        for (int i = 1; i < list.size(); i++) {
            temp.next = list.get(i);
            temp = temp.next;
        }
        temp.next = null;
        return resNode;
    }
}

(2)方法二：快慢指针

public ListNode removeNthFromEnd(ListNode head, int n) {
        // write code here
        if (head == null) {
            return head;
        }
  
        ListNode left = head;
        ListNode right = head;
        //right指针先走n步
        for (int i = 0; i < n; i++) {
            right = right.next;
        }
        //此时right可能为null 把头节点删除
        if (right == null) {
            head = head.next;
            return head;
        }
        //遍历，直至right.next为null，此时right就是链表的最后一个节点
        while (right.next != null) {
            left = left.next;
            right = right.next;
        }
        //那么left.next就是需要删除的node   
        //target.next至少为right，所以不可能为null
        //此时只需要把target节点删除即可
        ListNode target = left.next;
        left.next = target.next;
        target.next = null;
 
        return head;
}

大数加法

(1)从尾部插入

public String solve(String s, String t) {
  StringBuilder stringBuilder = new StringBuilder();
  int i = s.length() - 1, j = t.length() - 1, carry = 0;
  while (i >= 0 || j >= 0 || carry != 0) {
    int x = i < 0 ? 0 : s.charAt(i--) - '0';
    int y = j < 0 ? 0 : t.charAt(j--) - '0';
    int sum = x + y + carry;
    stringBuilder.append(sum % 10);//添加到字符串尾部
    carry = sum / 10;
  }
  return stringBuilder.reverse().toString();//对字符串反转
}

（2）从头部插入

public String solve(String s, String t) {
  StringBuilder stringBuilder = new StringBuilder();
  int carry = 0, i = s.length() - 1, j = t.length() - 1;
  while (i >= 0 || j >= 0 || carry != 0) {
    int x = i < 0 ? 0 : s.charAt(i--) - '0';
    int y = j < 0 ? 0 : t.charAt(j--) - '0';
    int sum = x + y + carry;
    stringBuilder.insert(0, sum % 10);//插入到s字符串的第一个位置
    carry = sum / 10;
  }
  return stringBuilder.toString();
}

(3) 使用栈来解决

public String solve(String s, String t) {
  Stack<Integer> stack = new Stack<>();
  StringBuilder stringBuilder = new StringBuilder();
  int i = s.length() - 1, j = t.length() - 1, carry = 0;
  while (i >= 0 || j >= 0 || carry != 0) {
    carry += i >= 0 ? s.charAt(i--) - '0' : 0;
    carry += j >= 0 ? t.charAt(j--) - '0' : 0;
    stack.push(carry % 10);
    carry = carry / 10;
  }
  while (!stack.isEmpty())
    stringBuilder.append(stack.pop());
  return stringBuilder.toString();
}

按之字形顺序打印二叉树


（1）队列+List

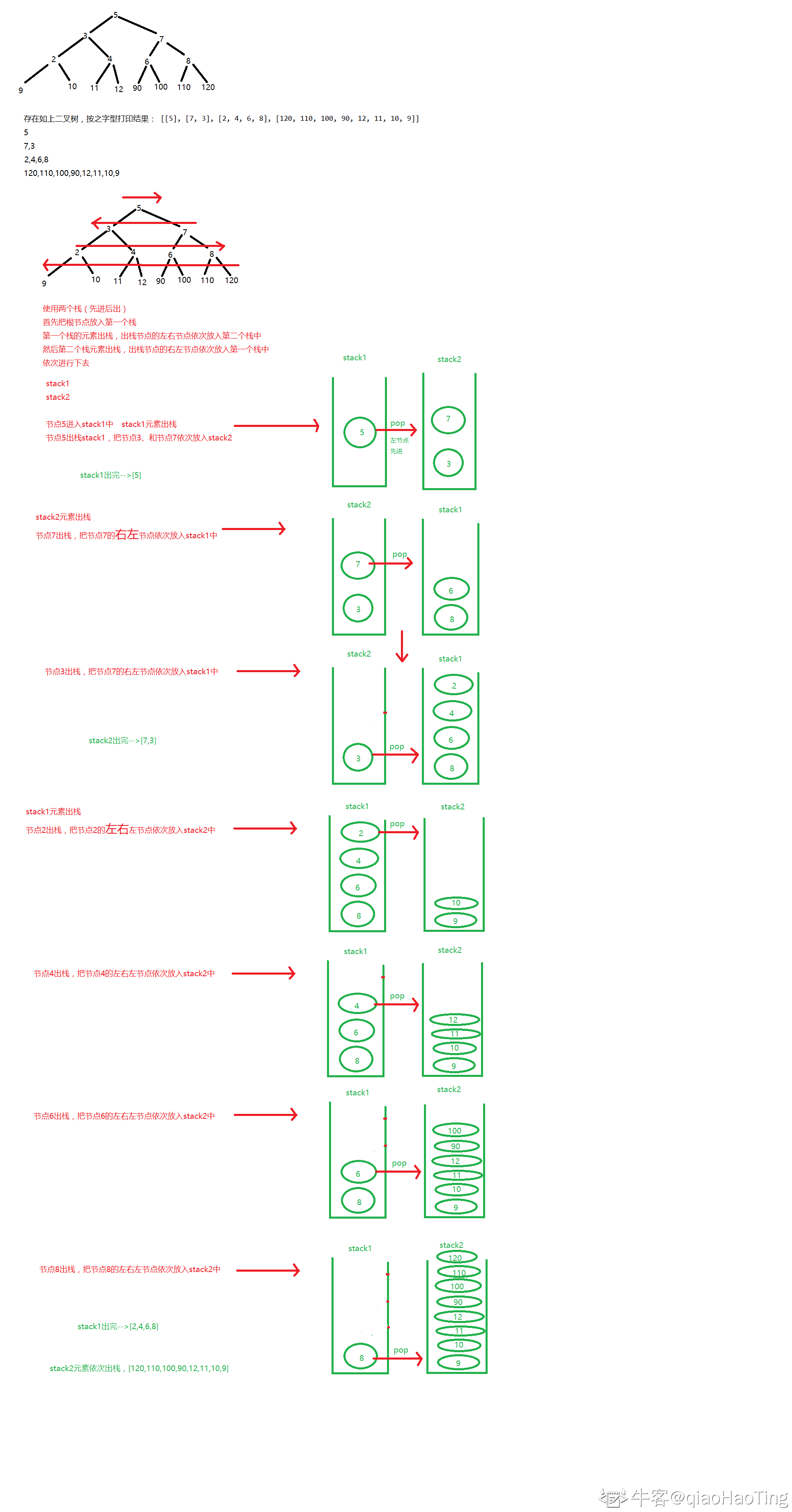
    //解题思路：其实就是二叉树的层级遍历，不过是在遍历的时候，需要将偶数层的节点逆序。
    //关键点：每次只处理上次在queue中剩余的节点，这是上一层的所有节点。
    //       处理完后刚好将下一层的所有节点（包含null）又全部放了进去。
    public ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
        ArrayList<ArrayList<Integer> > result=new ArrayList<>();
        if(pRoot==null){
            return result;
        }
        Queue<TreeNode> queue=new LinkedList<TreeNode>();
        queue.offer(pRoot);
        boolean reverse=false;
        while(!queue.isEmpty()){
            int size=queue.size();
            ArrayList<Integer> list=new ArrayList<>();
            for(int i=0;i<size;i++){
                TreeNode node=queue.poll();
                if(node==null){
                    continue;
                }
                if(!reverse){
                    list.add(node.val);
                }else{
                    list.add(0,node.val);//每次加到0的位置，就自动逆序了
                }
                queue.offer(node.left);
                queue.offer(node.right);
            }
            if(list.size()>0){
                result.add(list);
            }
            reverse=!reverse;
        }
        return result;
    }

写法2:

public class Solution {//方法2和方法1相比，代码区别仅仅是把stack相关删去，然后换成ArrayList头插法
    public ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
        ArrayList<ArrayList<Integer>> res = new ArrayList<ArrayList<Integer>>();
        if(pRoot == null)return res;
        ArrayList<TreeNode> queue = new ArrayList<TreeNode>();
        queue.add(pRoot);
        int layer = 1;
        while(!queue.isEmpty()){
            ArrayList<Integer> list = new ArrayList<Integer>();
            int size = queue.size();
            for(int i=0; i<=size-1; ++i){
                TreeNode node = queue.get(0);
                queue.remove(0);
                if(layer % 2 == 1){
                    list.add(node.val);
                }
                else{
                    list.add(0,node.val);//头插法，逆序 //【代码简洁，但效率比Stack低】
                }
                if(node.left != null)queue.add(node.left);
                if(node.right != null)queue.add(node.right);
            }
            res.add(list);
            ++layer;
        }
        return res;
    }
}//时间、空间都是 O(N)

（2）队列+栈

public class Solution {
    public ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
        ArrayList<ArrayList<Integer>> res = new ArrayList<ArrayList<Integer>>();
        if(pRoot == null)return res;
        Stack<Integer> stack = new Stack<Integer>();//stack仅用于偶数层翻转val
        ArrayList<TreeNode> queue = new ArrayList<TreeNode>();//queue是奇偶共用
        queue.add(pRoot);
        int layer = 1;//层数用layer (区别于深度depth = layer-1)
        while(!queue.isEmpty()){
            ArrayList<Integer> list = new ArrayList<Integer>();//新建行
            int size = queue.size();//出本层前记录size，不然难以做到层数的切分  //提前写出来，因为size会变
            for(int i=0; i<=size-1; ++i){
                TreeNode node = queue.get(0);//一定要新建node副本，不然是引用会变
                queue.remove(0);
                if(layer % 2 == 1){
                    list.add(node.val);
                } else{//偶数行，需要栈翻转
                    stack.push(node.val);
                }
                if(node.left != null)queue.add(node.left);
                if(node.right != null)queue.add(node.right);
            }
            while(!stack.isEmpty()){
                list.add(stack.pop());//偶数层一次性添加，奇数层一个个添加
            }
            res.add(list);
            ++layer;//本层结束，层数加一
        }
        return res;
    }
}//时间、空间复杂度，都是树的规模 O(N)

最长公共子串

(1) 解法1

public String LCS (String str1, String str2) {
  String result=new String();
  for(int i=0;i<str1.length();i++){
    int k=i;
    int count=0;
    for(int j=0; k<str1.length() && j<str2.length()  ;j++){
      if(str2.charAt(j)==str1.charAt(k)){
        count++;
        k++;
      }else{
        j=j-count;
        k=i;
        count=0;
      }
      if(count>result.length()){
        result=str1.substring(i,k);
      }
    }
  }
  return result;
}

(2)解法2

public String LCS (String str1, String str2) {
        int start = 0;
		int end = 1;
		StringBuilder s = new StringBuilder();
		while (end < str1.length()+1) {//注意是要加一，因substring函数是不包含上界
			if (str2.contains(str1.substring(start, end))) {
				if (s.length() < (end - start)) {
					s.delete(0, s.length());
					s.append(str1, start, end);
				}
				end++;
			} else {
				start++;
			}
		}
		if (s.length() == 0) {
			return "";
		}
		return s.toString();
}

(3)动态规划

public String LCS(String str1, String str2) {
    int maxLenth = 0;//记录最长公共子串的长度
    //记录最长公共子串最后一个元素在字符串str1中的位置
    int maxLastIndex = 0;
    int[] dp = new int[str2.length() + 1];
    for (int i = 0; i < str1.length(); i++) {
        //注意这里是倒序
        for (int j = str2.length() - 1; j >= 0; j--) {
            //递推公式，两个字符相等的情况
            if (str1.charAt(i) == str2.charAt(j)) {
                dp[j + 1] = dp[j] + 1;
                //如果遇到了更长的子串，要更新，记录最长子串的长度，
                //以及最长子串最后一个元素的位置
                if (dp[j + 1] > maxLenth) {
                    maxLenth = dp[j + 1];
                    maxLastIndex = i;
                }
            } else {
                //递推公式，两个字符不相等的情况
                dp[j + 1] = 0;
            }
        }
    }
    //最字符串进行截取，substring(a,b)中a和b分别表示截取的开始和结束位置
    return str1.substring(maxLastIndex - maxLenth + 1, maxLastIndex + 1);
}

两个链表的第一个公共结点

思路：遍历两遍这两个链表，如果有重复的节点，那么一定能够使遍历的指针相等。

（1）遍历

public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
    if(pHead1 == null || pHead2 == null)return null;
    ListNode p1 = pHead1;
    ListNode p2 = pHead2;
    while(p1!=p2){
        p1 = p1.next;
        p2 = p2.next;
        if(p1 != p2){
            if(p1 == null)p1 = pHead2;
            if(p2 == null)p2 = pHead1;
        }
    }
    return p1;

}

（2）集合Set

public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
    HashSet<ListNode> set=new HashSet<>();
    while(pHead1!=null){
        set.add(pHead1);
        pHead1=pHead1.next;
    }
    while(pHead2!=null){
        if(set.contains(pHead2))
            return pHead2;
        pHead2=pHead2.next;
    }
    return null;
}

链表相加(二)

import java.util.*;
public class Solution {
    //反转链表
    public ListNode ReverseList(ListNode pHead) { 
        if(pHead == null)
            return null;
        ListNode cur = pHead;
        ListNode pre = null;
        while(cur != null){
            //断开链表，要记录后续一个
            ListNode temp = cur.next;
            //当前的next指向前一个
            cur.next = pre; 
            //前一个更新为当前
            pre = cur; 
            //当前更新为刚刚记录的后一个
            cur = temp; 
        }
        return pre;
    }
    
    public ListNode addInList (ListNode head1, ListNode head2) {
        //任意一个链表为空，返回另一个
        if(head1 == null) 
            return head2;
        if(head2 == null)
            return head1;
        //反转两个链表
        head1 = ReverseList(head1); 
        head2 = ReverseList(head2);
        //添加表头
        ListNode res = new ListNode(-1); 
        ListNode head = res;
        //进位符号
        int carry = 0; 
        //只要某个链表还有或者进位还有
        while(head1 != null || head2 != null || carry != 0){ 
            //链表不为空则取其值
            int val1 = head1 == null ? 0 : head1.val; 
            int val2 = head2 == null ? 0 : head2.val;
            //相加
            int temp = val1 + val2 + carry; 
            //获取进位
            carry = temp / 10; 
            temp %= 10; 
            //添加元素
            head.next = new ListNode(temp); 
            head = head.next;
            //移动下一个
            if(head1 != null) 
                head1 = head1.next;
            if(head2 != null)
                head2 = head2.next;
        }
        //结果反转回来
        return ReverseList(res.next); 
    }
}

单链表的排序

import java.util.*;
public class Solution {
    //合并两段有序链表
    ListNode merge(ListNode pHead1, ListNode pHead2) { 
        //一个已经为空了，直接返回另一个
        if(pHead1 == null) 
            return pHead2;
        if(pHead2 == null)
            return pHead1;
        //加一个表头
        ListNode head = new ListNode(0); 
        ListNode cur = head;
        //两个链表都要不为空
        while(pHead1 != null && pHead2 != null){ 
            //取较小值的节点
            if(pHead1.val <= pHead2.val){ 
                cur.next = pHead1;
                //只移动取值的指针
                pHead1 = pHead1.next; 
            }else{
                cur.next = pHead2;
                //只移动取值的指针
                pHead2 = pHead2.next; 
            }
            //指针后移
            cur = cur.next; 
        }
        //哪个链表还有剩，直接连在后面
        if(pHead1 != null) 
            cur.next = pHead1;
        else
            cur.next = pHead2;
        //返回值去掉表头
        return head.next; 
    }
    
    public ListNode sortInList (ListNode head) {
        //链表为空或者只有一个元素，直接就是有序的
        if(head == null || head.next == null) 
            return head;
        ListNode left = head; 
        ListNode mid = head.next;
        ListNode right = head.next.next;
        //右边的指针到达末尾时，中间的指针指向该段链表的中间
        while(right != null && right.next != null){ 
            left = left.next;
            mid = mid.next;
            right = right.next.next;
        }
        //左边指针指向左段的左右一个节点，从这里断开
        left.next = null; 
        //分成两段排序，合并排好序的两段
        return merge(sortInList(head), sortInList(mid)); 
    }
}

判断一个链表是否为回文结构

(1) 使用栈

public boolean isPail(ListNode head) {
    ListNode temp = head;
    Stack<Integer> stack = new Stack();
    //把链表节点的值存放到栈中
    while (temp != null) {
        stack.push(temp.val);
        temp = temp.next;
    }

    //然后再出栈
    while (head != null) {
        if (head.val != stack.pop()) {
            return false;
        }
        head = head.next;
    }
    return true;
}

（2）后半部分反转

public boolean isPail(ListNode head) {
    ListNode fast = head, slow = head;
    //通过快慢指针找到中点
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
    }
    //如果fast不为空，说明链表的长度是奇数个
    if (fast != null) {
        slow = slow.next;
    }
    //反转后半部分链表
    slow = reverse(slow);

    fast = head;
    while (slow != null) {
        //然后比较，判断节点值是否相等
        if (fast.val != slow.val)
            return false;
        fast = fast.next;
        slow = slow.next;
    }
    return true;
}

//反转链表
public ListNode reverse(ListNode head) {
    ListNode prev = null;
    while (head != null) {
        ListNode next = head.next;
        head.next = prev;
        prev = head;
        head = next;
    }
    return prev;
}

链表的奇偶重排

public ListNode oddEvenList(ListNode head) {
    //如果链表为空，不用重排
    if(head == null) 
        return head;
    //even开头指向第二个节点，可能为空
    ListNode even = head.next; 
    //odd开头指向第一个节点
    ListNode odd = head; 
    //指向even开头
    ListNode evenhead = even; 
    while(even != null && even.next != null){
        //odd连接even的后一个，即奇数位
        odd.next = even.next; 
        //odd进入后一个奇数位
        odd = odd.next; 
        //even连接后一个奇数的后一位，即偶数位
        even.next = odd.next; 
        //even进入后一个偶数位
        even = even.next; 
    } 
    //even整体接在odd后面
    odd.next = evenhead; 
    return head;
}

删除有序链表中重复的元素-I

public ListNode deleteDuplicates (ListNode head) {
    //空链表
    if(head == null)  return null;
    //遍历指针
    ListNode cur = head; 
    //指针当前和下一位不为空
    while(cur != null && cur.next != null){ 
        //如果当前与下一位相等则忽略下一位
        if(cur.val == cur.next.val) {
            cur.next = cur.next.next;
        } else {
            cur = cur.next;
        }
    }
    return head;
}

删除有序链表中重复的元素-II

public ListNode deleteDuplicates(ListNode head) {
    //空链表
    if(head == null)  return null;
   
    ListNode res = new ListNode(0);
    //在链表前加一个表头
    res.next = head; 
    ListNode cur = res;
    while(cur.next != null && cur.next.next != null){ 
        //遇到相邻两个节点值相同
        if(cur.next.val == cur.next.next.val){ 
            int temp = cur.next.val;
            //将所有相同的都跳过
            while (cur.next != null && cur.next.val == temp) 
                cur.next = cur.next.next;
        } else {
            cur = cur.next;
        }
    }
    //返回时去掉表头
    return res.next; 
}

连续子数组的最大和

public int FindGreatestSumOfSubArray(int[] array) {
   int sum = 0;
    int max = array[0];
    for(int i=0;i<array.length;i++){
        // 优化动态规划，确定sum的最大值
        sum = Math.max(sum + array[i], array[i]);
        // 每次比较，保存出现的最大值
        max = Math.max(max, sum);
    }
    return max;
}

在二叉树中找到两个节点的最近公共祖先

递归：

public class Solution {
      public int lowestCommonAncestor(TreeNode root, int o1, int o2) {
        return helper(root, o1, o2).val;
    }

    public TreeNode helper(TreeNode root, int o1, int o2) {
        if (root == null || root.val == o1 || root.val == o2)
            return root;
        TreeNode left = helper(root.left, o1, o2);
        TreeNode right = helper(root.right, o1, o2);
        //如果left为空，说明这两个节点在root结点的右子树上，我们只需要返回右子树查找的结果即可
        if (left == null) return right;
        //同上
        if (right == null) return left;
        //如果left和right都不为空，说明这两个节点一个在root的左子树上一个在root的右子树上，
        //我们只需要返回cur结点即可。
        return root;
    }
}

迭代：

public int lowestCommonAncestor(TreeNode root, int o1, int o2) {
    //记录遍历到的每个节点的父节点。
    Map<Integer, Integer> parent = new HashMap<>();
    Queue<TreeNode> queue = new LinkedList<>();
    parent.put(root.val, Integer.MIN_VALUE);
    queue.add(root);
    //直到两个节点都找到为止。
    while (!parent.containsKey(o1) || !parent.containsKey(o2)) {
        //队列是一边进一边出，这里poll方法是出队，
        TreeNode node = queue.poll();
        if (node.left != null) {
            //左子节点不为空，记录下他的父节点
            parent.put(node.left.val, node.val);
            //左子节点不为空，把它加入到队列中
            queue.add(node.left);
        }
        //右节点同上
        if (node.right != null) {
            parent.put(node.right.val, node.val);
            queue.add(node.right);
        }
    }
    Set<Integer> ancestors = new HashSet<>();
    //记录下o1和他的祖先节点，从o1节点开始一直到根节点。
    while (parent.containsKey(o1)) {
        ancestors.add(o1);
        o1 = parent.get(o1);
    }
    //查看o1和他的祖先节点是否包含o2节点，如果不包含再看是否包含o2的父节点……
    while (!ancestors.contains(o2))
        o2 = parent.get(o2);
    return o2;
}

最长回文子串

public class Solution {
 
    public int getLongestPalindrome (String A) {
        return getLongestPalindrome(A, A.length());
    }
    
    public int getLongestPalindrome(String A, int n) {
        if (n < 2) return A.length();

        int maxLen = 1;     //maxLen表示最长回文串的长度
        boolean[][] dp = new boolean[n][n];
        for (int right = 1; right < n; right++) {
            for (int left = 0; left <= right; left++) {
                //如果两种字符不相同，肯定不能构成回文子串
                if (A.charAt(left) != A.charAt(right))
                    continue;

                //下面是s.charAt(left)和s.charAt(right)两个
                //字符相同情况下的判断
                //如果只有一个字符，肯定是回文子串
                if (right == left) {
                    dp[left][right] = true;
                } else if (right - left <= 2) {
                    //类似于"aa"和"aba"，也是回文子串
                    dp[left][right] = true;
                } else {
                    //类似于"a******a"，要判断他是否是回文子串，只需要
                    //判断"******"是否是回文子串即可
                    dp[left][right] = dp[left + 1][right - 1];
                }
                //如果字符串从left到right是回文子串，只需要保存最长的即可
                if (dp[left][right] && right - left + 1 > maxLen) {
                    maxLen = right - left + 1;
                }
            }
        }
        //最长的回文子串
        return maxLen;
    }
}

最长上升子序列(三)

    public int[] LIS (int[] arr) {
        int len = 1, n = arr.length;
        if (n == 0) return new int[0];

        int[] d = new int[n + 1];
        int[] w = new int[n];
        d[len] = arr[0];
        w[0] = len;
        for (int i = 1; i < n; ++i) {
            if (arr[i] > d[len]) {
                d[++len] = arr[i];
                w[i] = len;
            } else {
                int l = 1, r = len, pos = 0;
                while (l <= r) {
                    int mid = (l + r) >> 1;
                    if (d[mid] < arr[i]) {
                        pos = mid;
                        l = mid + 1;
                    } else {
                        r = mid - 1;
                    }
                }
                d[pos + 1] = arr[i];
                w[i] = pos + 1;
            }
        }
        int[] res = new int[len];
        for (int i = n - 1, j = len; j > 0; --i) {
            if (w[i] == j) {
                res[--j] = arr[i];
            }
        }
        return res;
    }

接雨水问题

public long maxWater (int[] arr) {
    //排除空数组
    if(arr.length == 0) return 0;
    long res = 0;
    //左右双指针
    int left = 0;
    int right = arr.length - 1;
    //中间区域的边界高度
    int maxL = 0;
    int maxR = 0;
    //直到左右指针相遇
    while(left < right){
        //每次维护往中间的最大边界
        maxL = Math.max(maxL, arr[left]);
        maxR = Math.max(maxR, arr[right]);
        //较短的边界确定该格子的水量
        if(maxR > maxL)
            res += maxL - arr[left++];
        else
            res += maxR - arr[right--];
    }
    return res;
}

买卖股票的最好时机(一)

public int maxProfit (int[] prices) {
    int min = prices[0];
    int max = 0;
    for(int i=0;i<prices.length;i++){
        min=Math.min(prices[i],min);
        max=Math.max(max,prices[i]-min);
    }
    return max;
}

矩阵的最小路径和

public int minPathSum(int[][] matrix) {
    int m = matrix.length, n = matrix[0].length;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (i == 0 && j == 0)
                continue;
            if (i == 0) {
                //第一行只能从左边走过来
                matrix[i][j] += matrix[i][j - 1];
            } else if (j == 0) {
                //第一列只能从上面走下来
                matrix[i][j] += matrix[i - 1][j];
            } else {
                //递推公式，取从上面走下来和从左边走过来的最小值+当前坐标的值
                matrix[i][j] += Math.min(matrix[i - 1][j], matrix[i][j - 1]);
            }
        }
    }
    return matrix[m - 1][n - 1];
}

动态规划：

public int minPathSum (int[][] matrix) {
    int m = matrix.length;
    int n = matrix[0].length;
    int dp[][] = new int[m][n];
    for(int i=0;i<m;i++){
        for(int j=0;j<n;j++){
            if(i==0&&j==0){
                dp[0][0]=matrix[0][0];
            }else if(i==0){
                dp[i][j] = matrix[i][j] + dp[i][j-1];
            }else if(j==0){
                dp[i][j] = matrix[i][j] + dp[i-1][j];
            }
            else{
                dp[i][j]= matrix[i][j] + Math.min(dp[i-1][j], dp[i][j-1]);
            }
        }
    }
    return dp[m-1][n-1];
}

最长公共子序列(二)

public String LCS (String s1, String s2) {
    int n = s1.length();
    int m = s2.length();
    int [][]dp = new int[n + 1][m + 1];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    if (dp[n][m] == 0) return "-1";
    
    StringBuilder sb = new StringBuilder();
    while (n > 0 && m > 0) {
        if (s1.charAt(n - 1) == s2.charAt(m - 1)) {
            sb.append(s1.charAt(n - 1));
            n--;
            m--;
        } else {
            if (dp[n - 1][m] > dp[n][m - 1]) {
                n--;
            } else {
                m--;
            }
        }
    }
    return sb.reverse().toString();
}

二分查找-I

public int search (int[] nums, int target) {
    int l = 0;
    int r = nums.length - 1;
    //从数组首尾开始，直到二者相遇
    while(l <= r){ 
        //每次检查中点的值
        int m = (l + r) / 2; 
        if(nums[m] == target)
            return m;
        //进入左的区间
        if(nums[m] > target) 
            r = m - 1;
        //进入右区间
        else 
            l = m + 1;
    }
    //未找到
    return -1; 
}

二维数组中的查找

（1）从左下角找

public boolean Find(int target, int [][] array) {
    int rows = array.length;
    if(rows == 0){
        return false;
    }
    int cols = array[0].length;
    if(cols == 0){
        return false;
    }
    // 左下
    int row = rows-1;
    int col = 0;
    while(row>=0 && col<cols){
        if(array[row][col] < target){
            col++;
        }else if(array[row][col] > target){
            row--;
        }else{
            return true;
        }
    }
    return false;
}

（2）从右上角找

public boolean Find(int target, int [][] array) {
    int rows = array.length;
    if(rows == 0){
        return false;
    }
    int cols = array[0].length;
    if(cols == 0){
        return false;
    }
    // 右上
    int row = 0;   //注意
    int col = cols-1;    //注意
    while(row<rows && col>=0){    //注意
        if(array[row][col] < target){
            row++;        //注意
        }else if(array[row][col] > target){
            col--;      //注意
        }else{
            return true;
        }
    }
    return false;
}

寻找峰值

public int findPeakElement (int[] nums) {
    int left = 0;
    int right = nums.length - 1;
    //二分法
    while(left < right){ 
        int mid = (left + right) / 2;
        //右边是往下，不一定有坡峰
        if(nums[mid] > nums[mid + 1])
            right = mid;
        //右边是往上，一定能找到波峰
        else
            left = mid + 1;
    }
    return right; 
}

数组中的逆序对

public class Solution {
    public int mod = 1000000007;
    public int mergeSort(int left, int right, int [] data, int [] temp){
        //停止划分
        if(left >= right)    
            return 0;
        //取中间
        int mid = (left + right) / 2; 
        //左右划分合并
        int res = mergeSort(left, mid, data, temp) + mergeSort(mid + 1, right, data, temp); 
        //防止溢出
        res %= mod;  
        int i = left, j = mid + 1;
        for(int k = left; k <= right; k++)
            temp[k] = data[k];
        for(int k = left; k <= right; k++){
            if(i == mid + 1)
                data[k] = temp[j++];
            else if(j == right + 1 || temp[i] <= temp[j])
                data[k] = temp[i++];
            //左边比右边大，答案增加
            else{ 
                data[k] = temp[j++];
                // 统计逆序对
                res += mid - i + 1; 
            }
        }
        return res % mod;
    }
    
    public int InversePairs(int [] array) {
        int n = array.length;
        int[] res = new int[n];
        return mergeSort(0, n - 1, array, res);
    }
}

旋转数组的最小数字

（1）二分法

public int minNumberInRotateArray(int [] array) {
    int left = 0;
    int right = array.length - 1;
    while(left < right){
        int mid = (left + right) / 2;
        //最小的数字在mid右边
        if(array[mid] > array[right])
            left = mid + 1;
        //无法判断，一个一个试
        else if(array[mid] == array[right])
            right--;
        //最小数字要么是mid要么在mid左边
        else
            right = mid;
    }
    return array[left];
}

（2）遍历查找

public int minNumberInRotateArray(int [] array) {
    //数组一定有元素
    int res = array[0]; 
    //遍历数组
    for(int i = 1; i < array.length; i++) {
        //每次维护最小值
        res = Math.min(res, array[i]); 
    }
    return res;
}

比较版本号

public int compare(String version1, String version2) {
    String s1[] = version1.split("\\.");
    String s2[] = version2.split("\\.");

    int n1 = s1.length;
    int n2 = s2.length;
    int n = Math.max(n1, n2);
    int k1[] = new int[n];
    for (int i = 0; i < s1.length; i++) {
        k1[i] = Integer.valueOf(s1[i]);
    }

    int k2[] = new int[n];
    for (int i = 0; i < s2.length; i++) {
        k2[i] = Integer.valueOf(s2[i]);
    }

    for (int i = 0; i < n; i++) {
        if (k1[i] > k2[i]) {
            return 1;
        } else if (k1[i] < k2[i]) {
            return -1;
        }
    }
    return 0;
}