力扣每日一题48：旋转图像

题目描述：

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

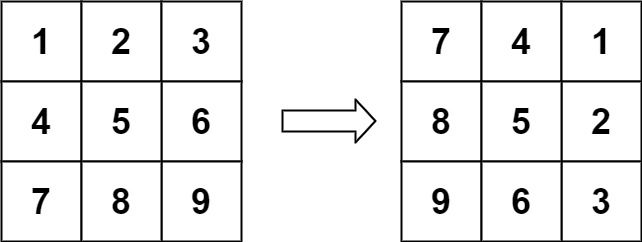
示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

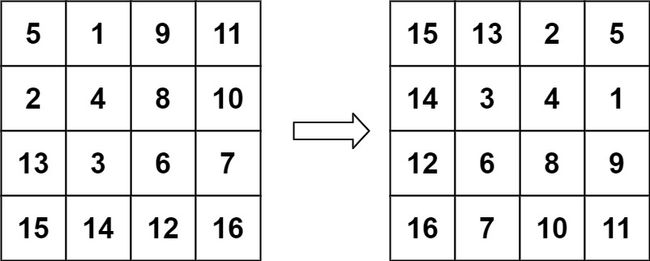
示例 2：

输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

• n == matrix.length == matrix[i].length
• 1 <= n <= 20
• -1000 <= matrix[i][j] <= 1000

通过次数

495.6K

提交次数

659.8K

通过率

75.1%

题解和思路：

方法一：外层旋转然后向内层收缩。

做一个循环，每次循环时旋转矩阵最外层回字型，然后矩阵向内收缩，直到收缩到一个2*2矩阵或一个1*1矩阵时就停止。

代码：

class Solution {
public:
    void rotate(vector>& matrix) {
        int n=matrix.size();
        int lo=0,hi=n-1;
        while(lo temp(hi-lo,0);
            //先换四个角，再换其它的
            int t=matrix[lo][lo];
            matrix[lo][lo]=matrix[hi][lo];
            matrix[hi][lo]=matrix[hi][hi];
            matrix[hi][hi]=matrix[lo][hi];
            matrix[lo][hi]=t;
            ///去角后的四条边
            for(int i=0;i左边
            for(int i=0;i下面
            for(int i=0;i右边
            lo++;
            hi--;
        }
    }
};

方法二：反转代替旋转

先将矩阵通过水平轴翻转（即第一行和最后一行换，第二行和倒数第二行换......），再通过主对角线翻转，最后得到的矩阵和将原数组顺时针旋转90°的矩阵是一样的。不信的话可以自己拿一个长方形的纸片试一试。官方题解有这种思路，我直接放官方题解代码吧。

代码：

class Solution {
public:
    void rotate(vector>& matrix) {
        int n = matrix.size();
        // 水平翻转
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < n; ++j) {
                swap(matrix[i][j], matrix[n - i - 1][j]);
            }
        }
        // 主对角线翻转
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                swap(matrix[i][j], matrix[j][i]);
            }
        }
    }
};