牛客小白月赛16

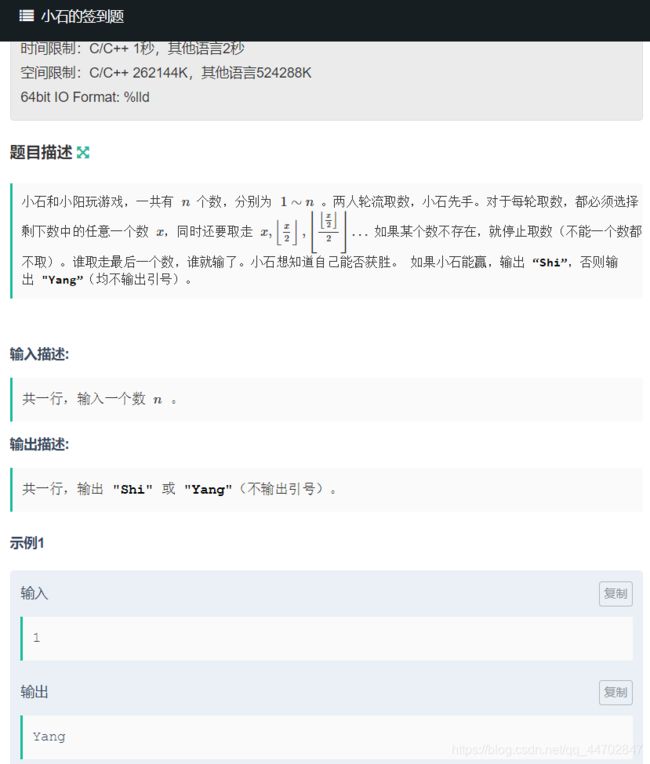
A题 小石的签到题

大声bb:

小石是先手,只有n=1的时候会输,否他都可以赢:>
因为,n=2的时候小石可以拿一剩下一个数,n=3的时候小石可以拿2剩下一个数,n=4的时候小石可以拿3也剩下一个数,n=5的时候,小石先拿1,然后把剩下的情况推一遍就知道小石会赢…
…只要小石保证他拿了之后不会让小杨拿了之后剩下一个数他就能赢,
换言之,在小石会输的情况下他可以只拿1这个数字…
官方题解
如何证明：一开始有 1∼n ,n个数，假设先手必败，那么先手选 1，后手就进入了必败状态。
所以假设错误，那么先手就不是必败，先手一定有一种方式能赢。

代码

#include 
#include 
#include 
#include 
#include 
using namespace std;
int main()
{
    int n;
    cin>>n;
    if(n == 1)printf("Yang\n");
    else printf("Shi\n");
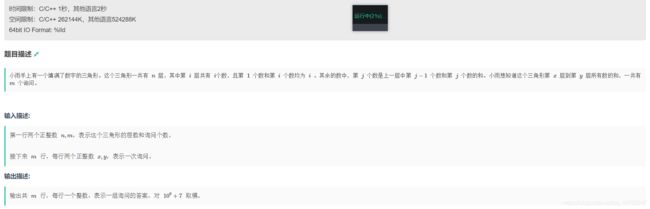
    return 0;
}

---

B题 小雨的三角形

大声bb:

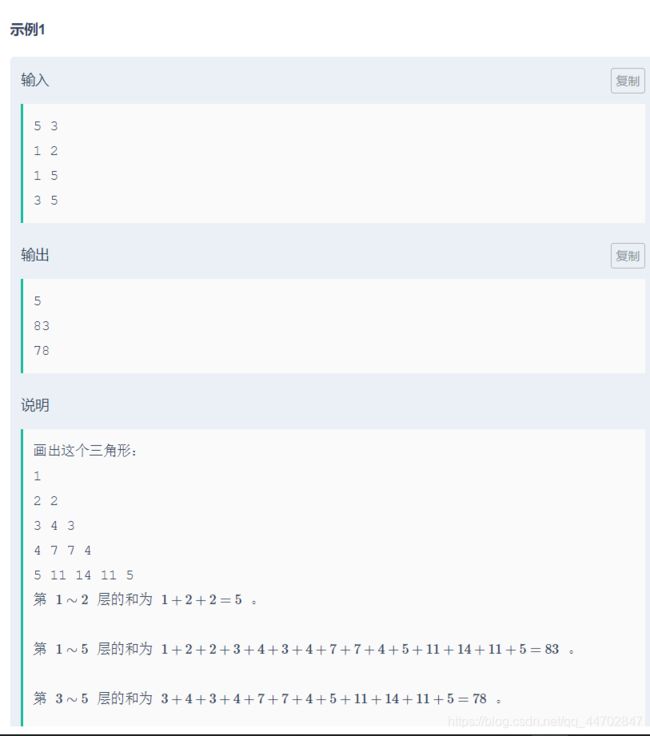
我是先画出三角形然后分别计算和得到了一个规律,我把每一行的和记成一个数组a,
a[n]=1,n=1
a[n]=2*a[n-1]+2,n>=2
然后计算,
wa了一次的原因是没有对a数组里面的值取模,计算结果不正确,好像是超过范围了吧…输出来看全是-2…

代码

#include 
#include 
#include 
#include 
#include 
#define ll long long
using namespace std;
ll a[1010]={0};
int main()
{
    int n,m;
    cin>>n>>m;
    a[1] = 1;
    for(int i = 2 ; i <= n ; i++){
        a[i] = (2 * a[i-1] + 2 + 1000000007)% 1000000007;
        //printf("%d : %d\n",i,a[i]);
    }
    int x,y;
    ll ans = 0;
    for(int k = 0 ; k < m ; k++){
        scanf("%d %d",&x,&y);
        ans = 0;
        for(int i = x; i <= y ; i++){
            ans+=a[i];
        }
        ans = (ans+1000000007) % 1000000007;
        if(k == m-1)    printf("%lld",ans);
        else printf("%lld\n",ans);
    }
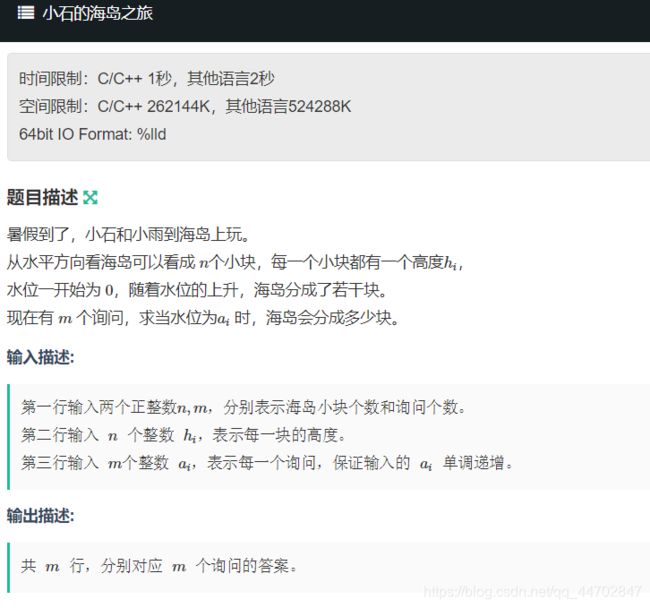
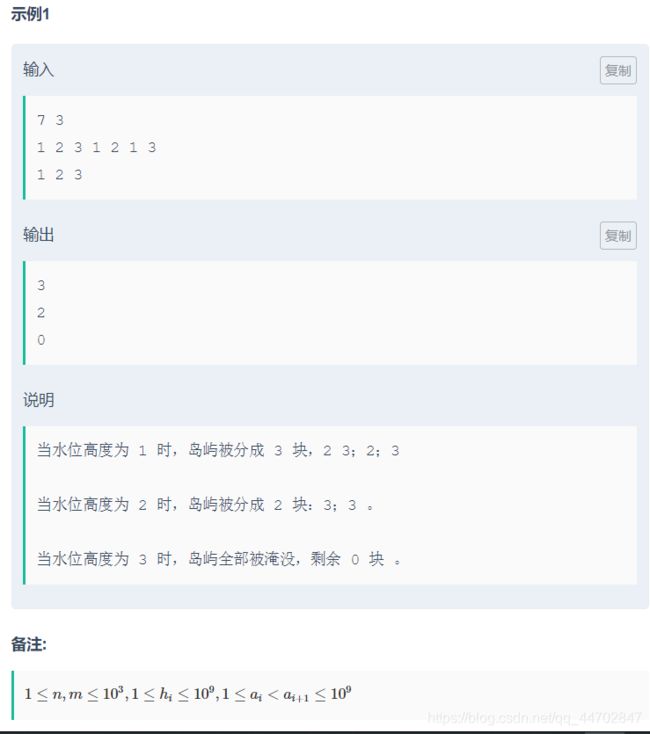
    return 0;
}

---

C题 小石的海岛之旅

大声bb

这题我当时想的是
直接找边界,(具体思路历程记不清了,也许是纠结中的灵光一现-)
然后打出来之后试了下特例可以放到条件里就没有加特判

代码

#include 
#include 
#include 
#include 
#include 
#define ll long long
using namespace std;

ll h[1010] = {0};
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i = 1 ; i <= n ; i++){
		scanf("%lld",&h[i]);
	}
	for(int k = 0 ; k < m ; k++){
		int x;
		scanf("%d",&x);
		int ans = 0;
		for(int i = 1 ; i <= n ; i++){
			if(h[i] > x && h[i-1] <= x) ans++;
		}
		if(k == m-1)printf("%d",ans);
		else printf("%d\n",ans);
	}
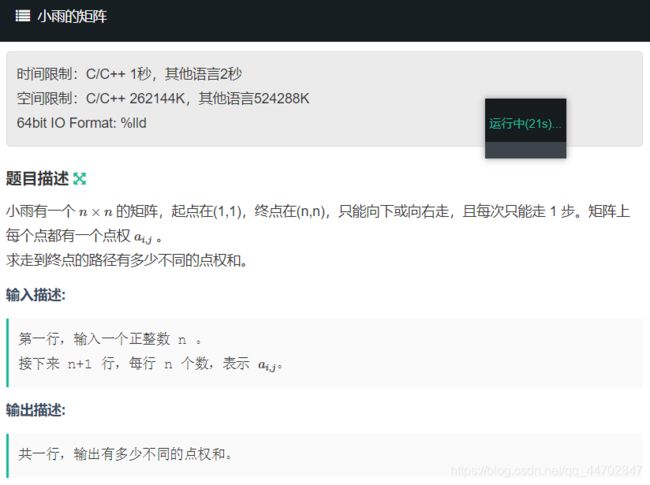
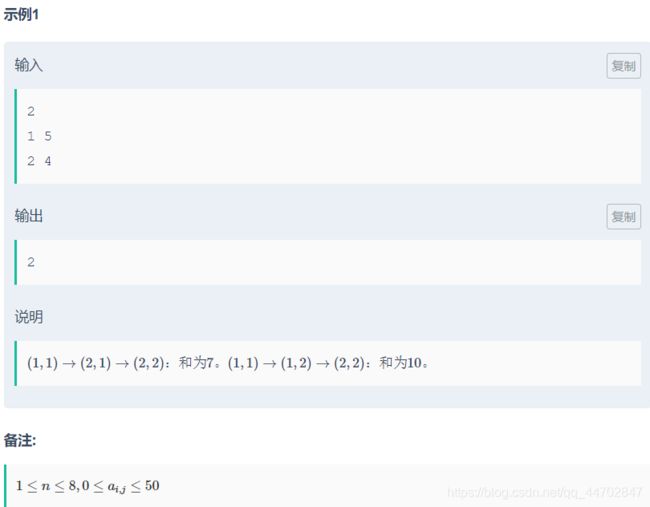
    return 0;
}

---

E题 小雨的矩阵

大声bb:

搜索 : > 然后去重
代码

#include 
#include 
#include 
#include 
#include 
#define ll long long
using namespace std;
int a[55][55]={0},b[505]={0};
int n;
int ans = 0;
void dfs(int x,int y,int count){
    if(x == n && y == n)    {
        int k;
        for(k = 0 ; k <= ans; k++){
            if(b[k] == count)break;
        }
        if(k > ans) b[ans++] = count;
        return ;   
    }
    if(x != n) dfs(x+1,y,count+a[x+1][y]);
    if(y != n) dfs(x,y+1,count+a[x][y+1]);
}
 
int main()
{
    cin>>n;
    for(int i = 1; i <= n; i++){
        for(int j = 1 ; j <= n ; j++){
            cin>>a[i][j];
        }
    }
    dfs(1,1,a[1][1]);
    printf("%d",ans);
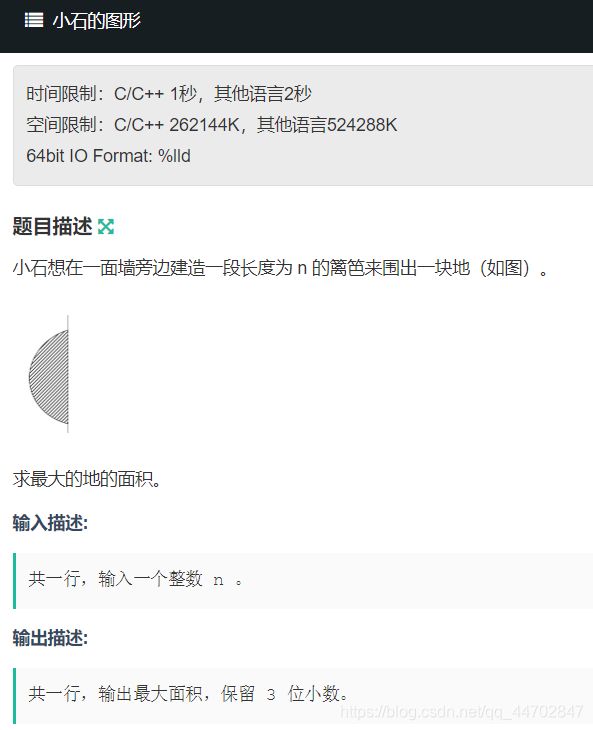
    return 0;
}

---

G题 小石的图形

大声bb:

最大面积是半圆,

代码

#include 
#include 
#include 
#include 
#include 
using namespace std;
int main()
{
    int n;
    cin>>n;
    double ans;
    ans = n * n * 1.0/(3.1415926535898 * 2);
    printf("%.3lf\n",ans);
    return 0;
}