并查集(2)---一文搞定并查集(求连通域)类型问题!
上一篇关于并查集的教学 见此博客
个人感悟
- 1.首先,看到题目描述 能抽象出节点,边以及寻找连通域等相关图论的模型,就可以尝试思考并查集。
- 2.其次,要明确节点及其个数n,用来初始化并查集;
- 3.再明确节点对或者叫边的定义及个数m,并查集合并时遍历的就是m条边;
- 3.1 其中有的题很直白,节点和边的定义给的很明确,就直接套模板写代码就好,最多就是在定义并查集时加一些计数或找完并查集做一些后处理返回答案;
- 3.2 有的题节点定义不明确,需要自己思考以什么为节点初始化并查集。如lc947题移除石头,既可以以石头id号构建,也可以以石头所在坐标(x,y)来构建,不同构建代码效率不同。
- 3.3 有的题需要在边的vector里加一些信息,并对边排个序再遍历合并。如lc1489去除关键边和伪关键边
- 3.4 最小生成树的题,一般需要自己定义一个结构体记录在vector中,结构体包含两个节点和算出的边的权重。也都需要先按权重排完序再遍历合并
- 3.5 最难的就是题意表达很难直接联想到如何应用并查集,如下面的lc803打砖块,需要逆向思维才能应用到并查集上。
6. leetcode803. 打砖块
有一个 m x n 的二元网格,其中 1 表示砖块,0 表示空白。砖块 稳定(不会掉落)的前提是:
一块砖直接连接到网格的顶部,或者 至少有一块相邻(4 个方向之一)砖块 稳定 不会掉落时 给你一个数组 hits,这是需要依次消除砖块的位置。每当消除 hits[i] = (rowi, coli)位置上的砖块时,对应位置的砖块(若存在)会消失,然后其他的砖块可能因为这一消除操作而掉落。一旦砖块掉落,它会立即从网格中消失(即,它不会落在其他稳定的砖块上)。
返回一个数组 result ,其中 result[i] 表示第 i 次消除操作对应掉落的砖块数目。
注意,消除可能指向是没有砖块的空白位置,如果发生这种情况,则没有砖块掉落。
思路分析
本题要想到使用并查集应该是很简单的,但是怎么用却很难。
正常情况下,并查集是用来解决连通性问题(本题具有该条件),但是并查集一般用来合并连通分量,而不是拆分连通分量(换句话说,在并查集里面,拆分连通分量是一个复杂的操作)
为什么要逆向思维使用并查集 ? 因为按题目要求,解题是需要拆分连通分量,而并查集一般作合并分量 拆分连通分量是一个很难维护的操作
所以反过来思考,将问题打碎砖块会掉落多少个砖块转化成补上砖块会新增多少个砖块粘到房顶
那么步骤就很简单了:
- 复制grid到copy,为什么要复制,遍历hits的时候需要判断该位置 【本来就是0(空白)还是在第二部中置的0(被打碎的砖块)】
- 因为需要打碎的砖块一定为1,所以如果要逆向思考,补上的砖块必须是0,所以先将hits中需要打碎的砖块在copy中置为0
- 因为房顶永远不会掉落,所以将房顶(copy第一行)初始化为一个连通分量S,只要其他连通分量与该连通分量相连了,便会粘到房顶上,不会掉落。
- 逆序遍历hits,将hits中的砖块重新补到copy中,同时计算每一步有多少个砖块会粘到房顶上。
需要注意的是:
这里,我们虚拟出了一个【房顶节点】,只要节点与【房顶节点】处于同一个连通分量,那么不管该连通分量的根节点是哪个节点,该连通分量里的所有节点都不会掉落。
所以我们可以使用并查集的【按秩合并】优化。
class UFSet{
public:
vector<int> fa, rank, size;//记录节点的根,秩,该节点代表联通域的节点数
//构造初始化并查集
UFSet(int n){
fa.resize(n);
rank.resize(n);
size.resize(n);
for(int i = 0; i < n; i++){
fa[i] = i;
rank[i] = 1;
size[i] = 1;
}
}
//查
int find(int x){
return fa[x] == x ? x : (fa[x] = find(fa[x]));
}
//并
void merge(int x, int y){
int rootx = find(x), rooty = find(y);
if(rootx != rooty){
if(rank[rootx] <= rank[rooty]){
fa[rootx] = rooty;
size[rooty] += size[rootx];
}else{
fa[rooty] = rootx;
size[rootx] += size[rooty];
}
//更新秩
if(rank[rootx] == rank[rooty]) rank[rooty]++;
}
}
//返回该连通域砖块个数
int get_size(int x){
int root = find(x);
return size[root];
}
};
class Solution {
public: //思路:将问题打碎砖块会掉落多少个砖块转化成补上砖块会新增多少个砖块粘到房顶
vector<vector<int>> dir = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};//坐标移动方向:上下左右
vector<int> hitBricks(vector<vector<int>>& grid, vector<vector<int>>& hits) {
int m = grid.size();//行数
int n = grid[0].size();//列数
int l = hits.size();//打掉砖的次数
vector<int> ans(l);//答案
//1.逆向初始化砖图
vector<vector<int>> copy(grid);
for(auto &v : hits){//把被打掉的砖置0
copy[v[0]][v[1]] = 0;
}
//2.构建初始天花板并查集(以砖块序号为单位,0~m*n-1),虚拟一个第m*n个节点代表天花板,与其相连都稳定
UFSet ufs(m * n + 1);
for(int j = 0; j < n; j++){
if(copy[0][j] == 0) continue;
ufs.merge(m * n, j);//先把第一行贴着天花板的砖都与天花板相连
}
for(int i = 1; i < m; i++){//继续把后面的砖块连上
for(int j = 0; j < n; j++){
if(copy[i][j] == 0) continue;
if(copy[i - 1][j] == 1){//上方有砖
ufs.merge(i * n + j, (i - 1) * n + j);
}
if(j > 0 && copy[i][j - 1] == 1){//左方有砖(勿忘判断边界j>0)
ufs.merge(i * n + j, i * n + j - 1);
}
}
}
//3.逆序取hits 置1补砖,看连通域能增加几块砖,增加的数即为会掉落的数
for(int k = l - 1; k >= 0; k--){//hits也要逆序取!!!
int i = hits[k][0], j = hits[k][1];
//若原本该位置就没砖,说明掉0块(不必赋值,初始化各位置就是0),找下一个
if(grid[i][j] == 0) continue;
int origin = ufs.get_size(m * n);//原本连在天花板上的稳定砖块数量
//若补回的砖靠着天花板,连上
if(i == 0) ufs.merge(m * n, j);
//若补回的砖在其他位置,更新并查集
for(auto &d : dir){
int r = i + d[0];
int c = j + d[1];//补回的砖的上,下,左, 右 的坐标
if(r < 0 || r >= m || c < 0 || c >= n || copy[r][c] == 0) continue;//不符合的过滤掉
ufs.merge(i * n + j, r * n + c);//补回的砖把两个连通域连在一起
}
int cur = ufs.get_size(m * n);//获取更新后的连通域中砖块数量
ans[k] = max(0, cur - origin - 1);
copy[i][j] = 1;//补上的砖 置1
}
return ans;
}
};
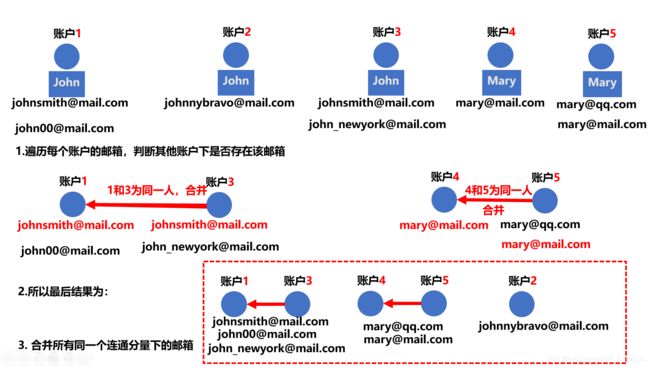
leetcode721. 账户合并
给定一个列表 accounts,每个元素 accounts[i] 是一个字符串列表,其中第一个元素 accounts[i][0] 是 名称
(name),其余元素是 emails 表示该账户的邮箱地址。
现在,我们想合并这些账户。如果两个账户都有一些共同的邮箱地址,则两个账户必定属于同一个人。请注意,即使两个账户具有相同的名称,它们也可能属于不同的人,因为人们可能具有相同的名称。一个人最初可以拥有任意数量的账户,但其所有账户都具有相同的名称。
合并账户后,按以下格式返回账户:每个账户的第一个元素是名称,其余元素是按顺序排列的邮箱地址。账户本身可以以任意顺序返回。
思路及分析
根据题意可知:
存在相同邮箱的账号一定属于同一个人
名称相同的账户不一定属于同一个人
由于名称相同无法判断为同1人,所以只能使用邮箱是否相同来判断是否为同一人。
这样建立并查集就比较简单了:
- 先初始化每个账户为1个连通分量 遍历每个账户下的邮箱,判断该邮箱是否在其他账户下出现 如果未出现,继续
- 如果账户A、B下出现了相同的邮箱email,那么将账户A和账户B两个连通分量进行合并
- 最后遍历并查集中每个连通分量,将所有连通分量内部账户的邮箱全部合并(相同的去重,不同的合并) 结束
class UFSet{
public:
//fa记录每个人名的根人名是谁(即含有相同邮箱的人名连在一起),都是以accounts下标序号idx为单位来构建并查集(避免人名重复)
vector<int> fa, rank;
UFSet(int n){
fa.resize(n);
rank.resize(n);
for(int i = 0; i < n; i++){
fa[i] = i;//每个人名idx初始指向自己
rank[i] = 1;
}
}
//查
int find(int x){
return fa[x] == x ? x : (fa[x] = find(fa[x]));
}
//并
void merge(int x, int y){
int fax = find(x), fay = find(y);
if(rank[fax] <= rank[fay]){
fa[fax] = fay;
}else{
fa[fay] = fax;
}
//更新秩
if(fax != fay && rank[fax] == rank[fay]) rank[fay]++;
}
};
//代码思路:
//1.根据邮箱和人名的对应关系,建立[邮箱:人名idx]的哈希表;
//2.根据人名idx(0~accounts.size()-1)构建并查集(避免了人名字符串构建时人名相同冲突的问题),把包含相同邮箱的人名idx连在一起。
//3.将合并好后的人名及邮箱存到unordered_map> newaccount中,set能自动去重排序
//4.将newaccount中内容转成题目要求的输出格式
class Solution {
public:
vector<vector<string>> accountsMerge(vector<vector<string>>& accounts) {
int n = accounts.size();
vector<vector<string>> ans;
unordered_map<string, int> email2name;//哈希表记录每个邮箱所属的人名idx,方便找到重复邮箱的人名idx 并链到一起
UFSet ufs(n);//初始化并查集,每个人名指向自己
//遍历每个邮箱,把含有相同邮箱的人名idx连在一起
for(int i = 0; i < n; i++){
for(int j = 1; j < accounts[i].size(); j++){
if(!email2name.count(accounts[i][j])){//若该邮箱第一次出现,则存入对应关系
email2name[accounts[i][j]] = i;//i为此时的人名下标
}else{//若邮箱重复出现了,则之前有该邮箱的人名和现在也包含该邮箱的人名连在一起
ufs.merge(email2name[accounts[i][j]], i);
}
}
}
// 遍历accounts中每个人名,寻找每个人名的根名字,并将该人名下所有邮箱保存到一起
// 由于会存在重复邮箱,且要考虑邮箱顺序,所以使用set来去重并内部自动排序
unordered_map<int, set<string>> newAcc;
for(int i = 0; i < n; i++){
int root = ufs.find(i);
for(int j = 1; j < accounts[i].size(); j++){
newAcc[root].insert(accounts[i][j]);//所有属于同一个人的邮箱都存在同一个人名下
}
}
//将newAcc转为题目要求的输出格式
for(auto &[k, s] : newAcc){
vector<string> sub;
sub.push_back(accounts[k][0]);//存入名字
for(auto &email : s) sub.push_back(email);//存入邮箱
ans.push_back(sub);
}
return ans;
}
};
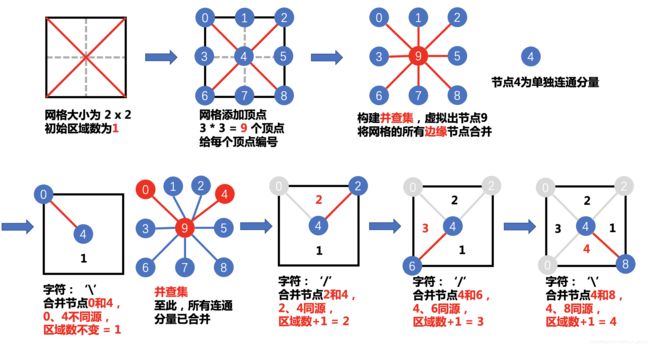
leetcode959. 由斜杠划分区域
在由 1 x 1 方格组成的 N x N 网格 grid 中,每个 1 x 1 方块由 /、
或空格构成。这些字符会将方块划分为一些共边的区域。 (请注意,反斜杠字符是转义的,因此 \ 用 “\” 表示。)。 返回区域的数目。
本题难点是 如何从题目描述中 抽象出 并查集模型。
本题解法多样:
1.并查集 2.DFS 3.BFS
其中,并查集的构建也有两种方式:
1.以方格中预先划分为4块的每一块idx作为节点合并
2.以方格每一个顶点为节点进行判断合并
篇幅有限,下面详细介绍定点构造并查集的方法。
思路
该题比较抽象,通过字符串来划分区域,看起来像是通过字符/和\来拆分区域,实则可以转化为顶点的合并,没错,又是并查集。
言归正传,这里使用了一个比较巧妙的转化: 要判断一个正方形被分割成了多少个区域,我们可以通过判断正方形内部有多少个封闭区域。
而要判断区域是否封闭,怎么办?明显,我们可以使用并查集:我们只需要访问区域的每个顶点,判断这些顶点是否构成环即可,如果构成环,便形成了封闭区域。
如何使用并查集判断单个连通分量中是否形成环? 那就很简单了:只需要在合并两个顶点时,判断两个顶点是否同源(根节点相同) 所以我们将一个N xN正方形划分成(N + 1) * (N +1)个顶点,然后根据正方形中的\和/来对顶点进行合并,同时判断形成了多少个封闭区域即可,具体过程见图例。
步骤
//并查集模板
class UFSet{
public:
vector<int> fa, rank;
int cnt;
//构造并查集
UFSet(int n): fa(n), rank(n, 1), cnt(1){
for(int i = 0; i < n; i++) fa[i] = i;
}
//查
int find(int x){
return fa[x] == x ? x : (fa[x] = find(fa[x]));
}
//并
void merge(int x, int y){
int fax = find(x), fay = find(y);
if(fax == fay){//找到根节点相同的说明成环了
cnt++;
}else{
if(rank[fax] > rank[fay]){
swap(fax, fay);
}
fa[fax] = fay;
if(rank[fax] == rank[fay]) rank[fay]++;
}
}
//返回答案
int get_cnt(){
return cnt;
}
};
/*
1.计算网格大小N,给网格添加N+1的平方个顶点,并进行编号;
2.构建并查集,将网格的所有边缘节点合并。这里的边缘节点是指位于网格边缘上的顶点; 遍历字符串数组grid中的字符,并作如下判断:
3.如果字符为空格 ,跳过, 如果字符为/,将小网格的左下和右上两个顶点合并, 如果字符为\,将小网格的左上和右下两个顶点合并。
4.如果两个顶点不同源(根节点不同),合并,区域数不变; 如果两个顶点同源(根节点相同),区域数 + 1; 最后判断生成了多少个封闭区域。
*/
class Solution {
public:
int regionsBySlashes(vector<string>& grid) {
int n = grid.size();//划分字符数组的大小,等同于方格有几行
if(n == 0) return 0;
int m = n + 1;//每行顶点个数
int num = m * m;//顶点总数
UFSet ufs(num + 1);//注意:因为有一个虚拟节点,此处初始化勿忘+1
//需要构造一个下标为num的虚拟节点将方格四个边上所有点先连在一起
for(int i = 0; i < num; i++){
if(i / m == 0 || i / m == m - 1 || i % m == 0 || i % m == m - 1){//上边,下边,左边,右边的点
ufs.merge(num, i);//四个边通过虚拟节点连在一起
}
}
//遍历grid根据字符来连接顶点
for(int i = 0; i < n; i++){
string s = grid[i];
for(int j = 0; j < s.length(); j++){
if(s[j] == '/'){
ufs.merge(i * m + j + 1, (i + 1) * m + j);//i理解成行,j理解成列,右上连到左下
}
if(s[j] == '\\'){
ufs.merge(i * m + j, (i + 1) * m + j + 1);//左上连到右下
}
}
}
//返回答案
int ans = ufs.get_cnt();
return ans;
}
};
此方法参考自:yex大佬的讲解
leetcode1579. 保证图可完全遍历
Alice 和 Bob 共有一个无向图,其中包含 n 个节点和 3 种类型的边:
类型 1:只能由 Alice 遍历。 类型 2:只能由 Bob 遍历。 类型 3:Alice 和 Bob 都可以遍历。给你一个数组edges ,其中 edges[i] = [typei, ui, vi] 表示节点 ui 和 vi 之间存在类型为 typei的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下,找出可以删除的最大边数。如果从任何节点开始,Alice 和 Bob都可以到达所有其他节点,则认为图是可以完全遍历的。
返回可以删除的最大边数,如果 Alice 和 Bob 无法完全遍历图,则返回 -1 。
思路
并查集的定义是固定写法。中间记录一下多余边个数
1.先合并公共的边,记录下 多余边个数 并 置0
2.依次分开 合并Alice的边,bob的边,并记录各自多余边的个数
3.判断Alice和bob有没有遍历完,都遍历完返回多余边之和,否则返回-1
注意:题中节点是从1开始的,这个要注意一下!!!
class UFSet{
public:
vector<int> fa,rank;
int extra;
//构造
UFSet(int n): fa(n), rank(n ,1), extra(0){
for(int i = 0; i < n; i++){
fa[i] = i;
}
}
//查
int find(int x){
return fa[x] == x ? x : (fa[x] = find(fa[x]));
}
//并
void merge(int x, int y){
int fax = find(x), fay = find(y);
if(fax == fay){
extra++;
}else{
if(rank[fax] > rank[fay]){
swap(fax, fay);
}
fa[fax] = fay;
if(rank[fax] == rank[fay]) rank[fay]++;
}
}
int get_extra(){
return extra;
}
};
//优先连公共的边,然后再分别连Alice和Bob的边,在连时遇到根相同的就extra边+1,最终判断两个有没有完全遍历在输出对应结果
class Solution {
public:
int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {
int m = edges.size();
int Pubextra, Aextra, Bextra;//Alice和Bob和公共的 的多余边
int Acnt = 0, Bcnt = 0;//记录Alice和Bob各自有几个连通域
UFSet ufs_public(n);//公共边的并查集,注意题目中节点从1开始
//1.先合并第三种公共边
for(int i = 0; i < m; i++){
if(edges[i][0] == 3){
ufs_public.merge(edges[i][1] - 1, edges[i][2] - 1);
}
}
Pubextra = ufs_public.get_extra();//记录公共边里的多余边
ufs_public.extra = 0;//勿忘置0
//2.合并Alice的边
UFSet Aufs = ufs_public;
for(int i = 0; i < m; i++){
if(edges[i][0] == 1){
Aufs.merge(edges[i][1] - 1, edges[i][2] - 1);
}
}
Aextra = Aufs.get_extra();
//看Alice能否完全遍历,!=1说明不能完全遍历
for(int i = 0; i < n; i++){
if(Aufs.find(i) == i) Acnt++;
}
//3.合并Bob的边
UFSet Bufs = ufs_public;
for(int i = 0; i < m; i++){
if(edges[i][0] == 2){
Bufs.merge(edges[i][1] - 1, edges[i][2] - 1);
}
}
Bextra = Bufs.get_extra();
//看Bob能否完全遍历
for(int i = 0; i < n; i++){
if(Bufs.find(i) == i) Bcnt++;
}
//判断如果都联通了,则返回所有多余边的和,否则-1
if(Acnt == 1 && Bcnt == 1){
return Aextra + Bextra + Pubextra;
}else{
return -1;
}
return -1;
}
};
leetcode1631. 最小体力消耗路径
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。
一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。
你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。
思路
1.看到该题联通路径,第一时间想到并查集,下面确定什么为节点,什么为边
2.节点显而易见,就是所有格子;边的话,每个点直连自己右边和下边的点即可全覆盖,并且据题意,需把消耗体力的信息也存入,故此处用了一个结构体保存边的信息(起始点,终点,耗费的体力);
3.节点和边确定了,并查集的实现就没啥了,固定写法,加一个保存当前最大体力的int值即可,合并时需要判断起始点0和最终点row*col-1是否联通,联通就返回,没有就继续找;
4.主调函数中要注意的是:存边信息时注意边界,合并前要先按照消耗体力的大小对 边vector集合 排个升序。
答题思路和要点如上,看代码和注释更好理解~
class UFSet{
public:
vector fa, rank;
int nums, maxconsume;//节点个数,最大体力消耗
UFSet(int n): fa(n), rank(n, 1), nums(n), maxconsume(0){
for(int i = 0; i < n; i++) fa[i] = i;
}
//查
int find(int x){
return fa[x] == x ? x : (fa[x] = find(fa[x]));
}
//并
bool merge(int x, int y, int consume){
int fax = find(x), fay = find(y);
if(fax == fay) return false;
if(rank[fax] > rank[fay]){
swap(fax, fay);
}
fa[fax] = fay;
maxconsume = max(maxconsume, consume);//记录当前花费的最大体力
if(rank[fax] == rank[fay]) rank[fay]++;
if(find(0) == find(nums - 1)) return true;//如果起始点和终点联通了,就返回
return false;
}
};
//定义存储路径边的结构体
struct path{
int start;//起始节点
int end;//到达的节点
int consume;//消耗的体力
};
class Solution {
public:
int minimumEffortPath(vector>& heights) {
int rows = heights.size();//行
int cols = heights[0].size();//列
UFSet ufs(rows * cols);
vector paths;//所有边的信息,每个点只连右边和下边的点
//1.保存好每条边的信息在paths中
//最右边一条竖边初始化
for(int i = 0; i < rows - 1; i++){
path p = {i * cols + cols - 1, (i + 1) * cols + cols - 1, abs(heights[i][cols - 1] - heights[i + 1][cols - 1])};//当前点 连 下方的点
paths.push_back(p);
}
//最下面一条边初始化
for(int j = 0; j < cols - 1; j++){
path p = {(rows - 1) * cols + j, (rows - 1) * cols + j + 1, abs(heights[rows - 1][j] - heights[rows - 1][j + 1])};//当前点 连 右侧的点
paths.push_back(p);
}
//处理剩下的格子
for(int i = 0; i < rows - 1; i++){
for(int j = 0; j < cols - 1; j++){
//当前点 连 下边的
path p = {i * cols + j, i * cols + j + 1, abs(heights[i][j] - heights[i][j + 1])};
paths.push_back(p);
//当前点 连 右边的
p = {i * cols + j, (i + 1) * cols + j, abs(heights[i][j] - heights[i + 1][j])};
paths.push_back(p);
}
}
//2.根据体力消耗consume对边排序
sort(paths.begin(), paths.end(), [](const auto &a, const auto &b){return a.consume < b.consume;});
//3.依次合并并查集
for(auto & pa : paths){
bool arrive = ufs.merge(pa.start, pa.end, pa.consume);
if(arrive) return ufs.maxconsume;//如果抵达就返回最大体力消耗
}
return 0;
}
};
leetcode778. 水位上升的泳池中游泳
在一个 N x N 的坐标方格 grid 中,每一个方格的值 grid[i][j] 表示在位置 (i,j) 的平台高度。
现在开始下雨了。当时间为 t 时,此时雨水导致水池中任意位置的水位为 t 。你可以从一个平台游向四周相邻的任意一个平台,但是前提是此时水位必须同时淹没这两个平台。假定你可以瞬间移动无限距离,也就是默认在方格内部游动是不耗时的。当然,在你游泳的时候你必须待在坐标方格里面。
你从坐标方格的左上平台 (0,0) 出发。最少耗时多久你才能到达坐标方格的右下平台 (N-1, N-1)?
思路
1.每个各自为一个节点,格子两两相连,两个个格子 高度取最大值 作为边的 权重,然后以权重对边的集合排升序
2.构建并查集,判断联通到最后一格子时返回最多的时间
和上面那题 leetcode1631. 最小体力消耗路径 一模一样,唯一区别是:上一题的权重存储的是每个节点间的体力消耗,这个权重存储的是两个节点的高度最大值。
详细思路参见 代码和注释~
class UFSet{
public:
vector<int> fa,rank;
int maxt, nums;//路径中最大雨水数,总节点个数
UFSet(int n): fa(n), rank(n, 1), maxt(0), nums(n){
for(int i = 0; i < n; i++) fa[i] = i;
}
//查
int find(int x){
return fa[x] == x ? x : (fa[x] = find(fa[x]));
}
//并
bool merge(int x, int y, int t){
int fax = find(x), fay = find(y);
if(fax == fay) return false;
if(rank[fax] > rank[fay]){
swap(fax, fay);
}
fa[fax] = fay;
if(rank[fax] == rank[fay]) rank[fay]++;
maxt = max(maxt, t);
if(find(0) == find(nums-1)) return true;
return false;
}
};
struct Edge{
int start;//起点
int end;//终点
int height;//高度
};
//思路:
//1.每个各自为一个节点,格子两两相连,两个个格子 高度取最大值 作为边的 权重,然后以权重对边的集合排升序
//2.构建并查集,判断联通到最后一格子时返回最多的时间
class Solution {
public:
int swimInWater(vector<vector<int>>& grid) {
int rows = grid.size();
int cols = grid[0].size();
int nums = rows * cols;
vector<Edge> Edges;
UFSet ufs(nums);
//1.所有点连在一起
for(int i = 0; i < rows; i++){
for(int j = 0; j < cols; j++){
if(i + 1 < rows){//连下面的点
Edge e = {i*cols+j, (i+1)*cols+j, max(grid[i][j], grid[i+1][j])};
Edges.push_back(e);
}
if(j + 1 < cols){//连右侧的点
Edge e = {i*cols+j, i*cols+j+1, max(grid[i][j], grid[i][j+1])};
Edges.push_back(e);
}
}
}
//2.按权重排升序
sort(Edges.begin(), Edges.end(), [](const auto &a, const auto &b){return a.height < b.height;});
//3.合并
for(const auto &e : Edges){
bool arrive = ufs.merge(e.start, e.end, e.height);
if(arrive) return ufs.maxt;
}
return 0;
}
};
leetcode839. 相似字符串组
如果交换字符串 X 中的两个不同位置的字母,使得它和字符串 Y 相等,那么称 X 和 Y
两个字符串相似。如果这两个字符串本身是相等的,那它们也是相似的。
例如,“tars” 和 “rats” 是相似的 (交换 0 与 2 的位置); “rats” 和 “arts” 也是相似的,但是
“star” 不与 “tars”,“rats”,或 “arts” 相似。
总之,它们通过相似性形成了两个关联组:{“tars”, “rats”, “arts”} 和 {“star”}。注意,“tars” 和
“arts” 是在同一组中,即使它们并不相似。形式上,对每个组而言,要确定一个单词在组中,只需要这个词和该组中至少一个单词相似。
给你一个字符串列表 strs。列表中的每个字符串都是 strs 中其它所有字符串的一个字母异位词。请问 strs 中有多少个相似字符串组?
思路
并查集的题做多了,就会发现其中的套路,这题思路很简单,就是套并查集模板,唯一要注意的是判断两个单词相似性。题目限定好了肯定都是异位词,所以只要判断不一样字母个数就可知道是否相似。其他详见下面代码和注释~
class UFSet{
public:
vector<int> fa, rank;
//初始化并查集
UFSet(int n): fa(n), rank(n,1){
for(int i = 0; i < n; i++) fa[i] = i;
}
//查
int find(int x){
return fa[x] == x ? x : (fa[x] = find(fa[x]));
}
//并
void merge(int x, int y){
int fax = find(x), fay = find(y);
if(fax == fay) return;
if(rank[fax] > rank[fay]){
swap(fax, fay);
}
fa[fax] = fay;
if(rank[fax] == rank[fay]) rank[fay]++;
}
};
/**
* 并查集
* 1 字符串数组中的每个字符看做一个单独节点
* 2 遍历字符串数组,将相似的两个节点合并(因为题中说了strs中全是彼此的字母异位词,只要判断两两间不同的字母个数为0或2即代表相似,否则不相似);
* 3 统计并返回该并查集中联通分量的个数
*/
class Solution {
public:
//判断是否相似的函数
bool checkSimilar(const string &a, const string &b, int len){
int nums = 0;
for(int i = 0; i < len; i++){
if(a[i] != b[i]) nums++;
}
if(nums == 0 || nums == 2) return true;
return false;
}
int numSimilarGroups(vector<string>& strs) {
int n = strs.size();//子字符串个数
int m = strs[0].size();//子字符长度
UFSet ufs(n);
int ans = 0;//统计连通域个数
for(int i = 0; i < n; i++){
for(int j = i + 1; j < n; j++){
//先判断是否已连上,已连上就不必再合并,可减少合并次数
if(ufs.find(i) == ufs.find(j)){
continue;
}
if(checkSimilar(strs[i], strs[j], m)){
ufs.merge(i, j);
}
}
}
//找合并完后有几个连通域
for(int i = 0; i < n; i++){
if(ufs.find(i) == i) ans++;
}
return ans;
}
};
力扣的并查月(1月)终于结束了,也顺利跟着每日的集训学会了并查集。个人感觉这种集训式的每日一题比随机各种类型的每日要好~
再补充一道
leetcode1722. 执行交换操作后的最小汉明距离
给你两个整数数组 source 和 target ,长度都是 n 。还有一个数组 allowedSwaps ,其中每个 allowedSwaps[i] = [ai, bi] 表示你可以交换数组 source 中下标为 ai 和 bi(下标从 0 开始)的两个元素。注意,你可以按 任意 顺序 多次 交换一对特定下标指向的元素。
相同长度的两个数组 source 和 target 间的 汉明距离 是元素不同的下标数量。形式上,其值等于满足 source[i] != target[i] (下标从 0 开始)的下标 i(0 <= i <= n-1)的数量。
在对数组 source 执行 任意 数量的交换操作后,返回 source 和 target 间的 最小汉明距离 。
思路
并查集模板好写,主要是要想到:
1.以什么为节点(此题为下标)
2.何为边(题中的可交换关系allowedSwaps)
3.合并完后如何后处理?(为每个联通分支维护位置的集合, key:value = 根下标:同属一一个联通区域(可交换)的数字集合;因为存在重复数字,所以value用unorder_multiset来存储;source和target各维护一个,然后s[i]中可交换的数,在t[i]中能找到则可以对应,否则距离+1)
代码胜过千言万语,详见代码和注释~
class UFSet{
public:
vector<int> fa, rank;
UFSet(int n): fa(n), rank(n, 1){
for(int i = 0; i < n; i++) fa[i] = i;
}
int find(int x){
return fa[x] == x ? x : (fa[x] = find(fa[x]));
}
void merge(int x, int y){
int fax = find(x), fay = find(y);
if(fax == fay) return;
if(rank[fax] > rank[fay]) swap(fax, fay);
fa[fax] = fay;
if(rank[fax] == rank[fay]) rank[fay]++;
}
};
class Solution {
public:
int minimumHammingDistance(vector<int>& source, vector<int>& target, vector<vector<int>>& allowedSwaps) {
int n = source.size();//数字个数
int ans = 0;
UFSet ufs(n);
for(const auto &a : allowedSwaps){
ufs.merge(a[0], a[1]);
}
// 为每个联通分支维护位置的集合, key:value = 根下标:同属一一个联通区域(可交换)的数字集合;因为存在重复数字,所以value用unorder_multiset来存储
unordered_map<int, unordered_multiset<int>> s, t;
for(int i = 0; i < n; i++){
int fai = ufs.find(i);
s[fai].insert(source[i]);
t[fai].insert(target[i]);
}
//s[i]中可交换的数,在t[i]中能找到则可以对应,否则距离+1
for(int i = 0; i < n; i++){
if(s.find(i) == s.end()) continue;
for(const auto &x : s[i]){
if(t[i].find(x) == t[i].end()){
ans++;
}else{
t[i].erase(t[i].find(x));// 不能使用 t[i].erase(x),不然会删掉所有的 x
}
}
}
return ans;
}
};