高数考研数学 基础知识篇

一、三角函数与反三角函数公式

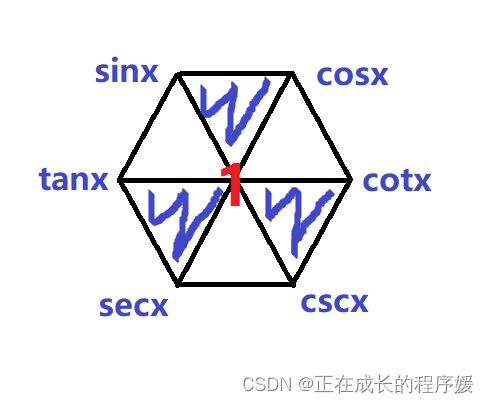
1. 三角函数基本关系

(1) 对角线上乘积为1：cscx = 1 / sinx , secx = 1 / cosx , cotx = 1 / tanx

(2) 顶点等于相邻两个顶点乘积: tanx = sinx / cosx , cotx = cosx / sinx

(3) 阴影三角形上两顶点的平方和等于下顶点的平方:

sin²x + cos²x =1 , 1 + tan²x = sec²x , 1 + cot²x = csc²x

2. 诱导公式

对于(kπ / 2) ± x (k ∈ Z) 的三角函数值

(1) 符号看象限: 把x看成0锐角,看(kπ / 2) ± x对应三角函数值的符号: (一正二正弦,三切四余弦)(即第一象限全部为正,第二象限只有sin为正,第三象限tan cot为正,第四象限只有cos为正)

(2) 奇变偶不变: 当k是偶数时,函数名不改变;当k是奇数时,函数名改变成相应的余函数值,即sin->cos , cos->sin , tan->cot , cot->tan

[例]

sin[(π / 2)  - x] = cosx

cos[(π / 2)  - x] = sinx

sin[(π / 2)  + x] = cosx

cos[(π / 2)  + x] = -sinx

sin(π - x) = sinx

cos(π - x) = -cosx

sin(π + x) = -sinx

cos(π + x) = -cosx

3. 二倍角公式

sin2x = 2sinxcosx , cos2x = cos²x - sin²x = 2cos²x - 1 = 1- 2sin²x

tan2x = 2tanx / (1 - tan²x) , cot2x = (cot²x - 1) / 2cotx

4. 半角公式(降幂公式)

sin²x = 1/2(1 - cos2x) , cos²x = 1/2(1+cos2x)

5. 和差公式

sin(x ± y) = sinxcosy ± cosxsiny ,

cos(x ± y) = cosxcosy ∓ sinxsiny , 

tan(x ± y) = (tanx ± tany) / (1 ∓ tanxtany) ,

cot(x ± y) = (cotxcoty ∓ 1) / (cotx ± coty) ,

asinx + bcosx = √ (a²+b²)    sin [x+arctan (b/a)]  (辅助角公式)

6. 积化和差公式

口诀:正余半正正 余余半余余 正正负半余减余

sinxcosy = 1/2[sin(x+y) + sin(x-y)]

cosxcosy = 1/2[cos(x+y) + cos(x-y)]

sinxsiny = -1/2[cos(x+y) - cos(x-y)]

7. 和差化积公式

口诀:正+正 二正余 正减正 二余正 余加余 二余余 余减余 负二正正

sinx+siny = 2sin (x+y)/2 cos (x-y)/2

sinx-siny = 2cos (x+y)/2 sin (x-y)/2

cosx+cosy = 2cos (x+y)/2 cos (x-y)/2

cosx-cosy = -2sin (x+y)/2 sin (x-y)/2

8. 万能公式

若t = tan(x/2) (-π

则sinx = 2t/(1+t²) , cosx = (1-t²)/(1+t²)

9.反三角函数基本关系

arcsinx + arccosx = π/2 (-1<=x<=1) , arctanx + arccotx = π/2 (-∞

二、代数与方程

1. 指数对数运算法则

aᵐ·aⁿ = aᵐ⁺ⁿ , (aᵐ)ⁿ = a(ᵐⁿ) , (ab)ⁿ = aⁿbⁿ ,  a^-1 = 1/a , ⁿ√a = a^(1/n) , a⁰=1 , √a² = |a| ,

lna + lnb =ln(ab) , ln(a/b) = lna - lnb , lnaⁿ =nlna , a = e^lna 

2. 常用数列

(1)等差数列: 首项为a1,公差为d(d!=0)

通项: an=a1+ (n-1)d

前n项和：Sn=n(a1+an)/2 

(2)等比数列: 首项为a1,公比为q(q!=0)

通项: an=a1q^(n-1)

前n项和:

Sn= na1  q=1 , 

    = [a1(1-q^n)] / (1-q)  q!=1

3. 因式分解公式

(a ± b)² = a² ± 2ab + b² 

(a ± b)³ = a³ ± 3a²b + 3ab² ± b³

a² - b² = (a + b)(a - b)

a³ - b³ = (a - b)(a² + ab + b²)

a³ + b³ = (a + b)(a² - ab + b²)

三、常用不等式

x-1 < [x] <= x < [x]+1

||a|-|b|| <= |a±b| <= |a|+|b|

x/(1+x) < ln(1+x) 0)

e^x >=x+1

sinx < x (x>0)

sinx < x < tanx (0

2/[(1/a)+(1/b)] <= √(ab) <= (a+b)/2 <= √[(a²+b²)/2]  (a,b>0)

四、阶乘与双阶乘

1. 阶乘：表示一个正整数与比它小的所有正整数之积。

例：

规定0！=1

3！=3*2*1

5！=5*4*3*2*1

2. 双阶乘：正整数的双阶乘表示不超过这个正整数且与它有相同奇偶性的所有正整数的乘积。

例：

1！！=1，

2！！=2，

4！！=2*4=8，

5！！=1*3*5=15，

6！！=2*4*6=48