并查集(Find-Union)解决无向图连通数量问题

性质

无向图中的边点关系满足三个性质：

1. 对称性：A和B联通，B和A也联通
2. 对称性：AB连通，BC连通，AC也连通
3. 自反性：自己对自己联通

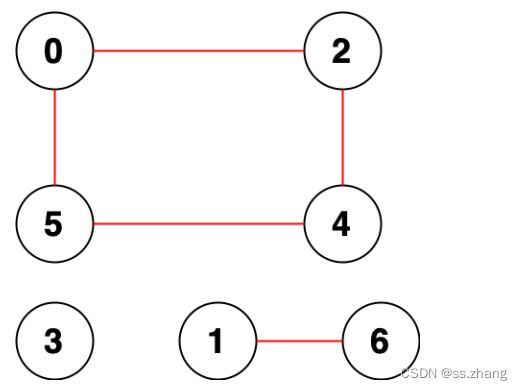
例如：统计无向图中无法互相到达点对数
给你一个整数 n ，表示一张 无向图 中有 n 个节点，编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。
请你返回 无法互相到达 的不同 点对数目 。

输入：n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
输出：14
解释：总共有 14 个点对互相无法到达：
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
所以我们返回 14 。

思路

一个连通集中的节点之间都能互相到达，而且都无法到达的节点个数都是相等的。如0245属于同一个联通集，互相连通，且无法到达的点书也相同。
如何表示边点的关系呢，如上图
可以将【0，1，2，3，4，5，6】表示为【0，1，0，3，0，0，1】

#初始化数组输出对应
p = [i for i in range(n)]

#连通
#e		dge表示所有边关系
        # [[0,2],[0,5],[2,4],[1,6],[5,4]]
        for i in edge:
            union(i[0],i[1])
        
        # union函数通过find可以找到给定点的根联通点
        # 如【0，2】的根分别是【0，2】，使用较小的点作为根，都用0表示
        # 【0，5】都用0表示，【2.4】中2的根为也用0表示，【1，6】都用1表示，【5，		  4】中根都是0，都用0表示
        def union(x,y):
            x = find(x)
            y = find(y)
            if x<=y:p[y] = x
            else:p[x] = y
            return
            
        #找到结点的联通集的根 
        #通过while循环的判断当前索引是否和值相同，
        #相同表示还没有并入其他连通集，
        #不同表示已经在之前做了变化，要继续寻找根点，由当前索引的值作为索引再次寻找
        #直到寻找到根，根满足索引与值相等的条件，停止循环
        def find(x):
            while x!=p[x]:
                x = p[p[x]]
            return x

D:\evo\anaconda\python.exe C:/onedrive/leetcode/test.py
p数组的变化过程如下：
	  [0, 1, 2, 3, 4, 5, 6]
[0,2],[0, 1, 0, 3, 4, 5, 6]
[0,5],[0, 1, 0, 3, 4, 0, 6]
[2,4],[0, 1, 0, 3, 0, 0, 6]
[1,6],[0, 1, 0, 3, 0, 0, 1]
[5,4],[0, 1, 0, 3, 0, 0, 1]

统计有多少个独立的连通集，每个连通集中有多少个节点。设连通集内节点个数=c，每个连通集贡献无法互相到达节点个数=(n-c)*c，累加res。就可以获得结果了，但是由于是双向计算2次，答案除以2。

        cnt = dict()
        for i in range(n):
        #找到当前点的根
            root = find(i)
            if root  in cnt:cnt[root]+=1
            #初始化点数为1
            else:cnt[root ] = 1

#三个连通集，其中结点三为独立
{0: 4, 1: 2, 3: 1}

		#计算互不连通的点的数量
        for i in cnt.values():
            res += (n-i)*i
        print(res/2)

14

完整代码

class Solution:
    def countPairs(self, n, edge):
        res = 0
        p = [i for i in range(n)]
        
        def find(x):
            while x!=p[x]:x = p[p[x]]
            return x
            
        def union(x,y):
            x = find(x)
            y = find(y)
            if x<=y:p[y] = xe
            else:p[x] = y
            return
            
        for e in edge:
            union(e[0],e[1])
            
        cnt = dict()
        for i in range(n):
            x = find(i)
            if x in cnt:cnt[x]+=1
            else:cnt[x] = 1
            
        for i in cnt.values():
            res += (n-i)*i
            
        return int(res/2)