STL之关联式容器----红黑树
-
标准STL关联式容器分为set(集合)和map(映射表)两大类以及这两大类的衍生体multiset(多键集合)和multimap(多键映射表),这些容器的底层机制均以RB-tree红黑树完成。它也是一个独立容器,但不开放给外界用
-
不在标准规格之列的关联式容器hash table(散列表/哈希表),和以hash table为底层机制的hash_set(散列集合)、hash_map(散列映射表)、hash_multiset(散列多键集合)、hash_multimap(散列多键映射表)
所谓关联式容器定义:
每个元素都有一个键值(key)和一个实值(value)。
当元素被插入到关联式容器中时,容器内部结构(可能是RB-tree,也可能是hash-table)便依照其键值大小,以某种特定规则将这个元素放置于适当位置。
关联式容器没有所谓头尾(只有最大最小元素),所以不会有push_back()、push_front()等这样的行为。
关联式容器的内部结构是一个平衡二叉树:包括AVL-tree、RB-tree、AA-tree,其中最被广泛运用于STL的是RB-tree
平衡二叉树:
AVL-tree(平衡二叉树):是一个加了“额外平衡条件”的二叉搜索树,其平衡条件的建立是为了保证整棵树的深度是O(logN)。任何结点的左右子树的高度相差最多是1
最小不平衡子树:距离插入结点最近的,且平衡因子的绝对值大于1的结点为根的子树。
AVL-tree的实现原理:在构建二叉排序树的过程中,每当插入一个结点时,先检查是否因插入而破坏了树的平衡性。若是,则找出最小不平衡子树。在保持二叉排序树特性的前提下,调整最小不平衡子树中各个结点之间的连接关系,进行相应的旋转,使之成为新的平衡子树。
调整规则:
当最小不平衡子树根结点的平衡因子BF大于1时,就右旋,小于-1时就左旋。
旋转之前先检查:插入节点后,当最小不平衡子树BF与他的子树的BF符号相反时,就需要对其子树进行一次旋转使得符号相同后,再反向旋转一次才能够完成平衡操作。具体见大话数据结构P333。
底层容器RB-tree(红黑树)
是高度平衡的二分搜索树
平衡二分搜索树的特点:排列规则有利于search和insert,并保持高度平衡即没有任何一个结点过深。
性质:
1. 节点是红色或黑色。
2. 根节点是黑色。
3. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点) (新增结点的父节点必须为黑)
4. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。 (新增结点必须为红)
性质3和性质4保证了其平衡性,所以在最坏的情况下它的查找和删除等操作是优于普通二叉排序树的。
红黑树的时间复杂度,由于它是基于排序二叉树的,所以它的查找和排序二叉树相同,都为O(log(n))。
插入结点
我们首先根据二叉搜索树的规则和新增结点必须为红的规则插入结点,如果此时破坏了RBtree的规则,就旋转树形并改变结点颜色。
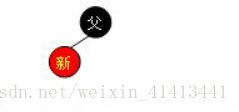
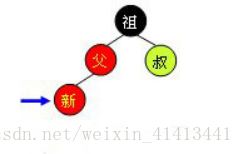
为了清楚地表示插入操作以下在结点中使用“新”字表示一个新插入的结点;使用“父”字表示新插入点的父结点;使用“叔”字表示“父”结点的兄弟结点;使用“祖”字表示“父”结点的父结点。插入操作分为以下几种情况:
1、黑父
如下图所示,如果新节点的父结点为黑色结点,那么插入一个红点将不会影响红黑树的平衡,此时插入操作完成。红黑树比AVL树优秀的地方之一在于黑父的情况比较常见,从而使红黑树需要旋转的几率相对AVL树来说会少一些。
2、红父
如果新节点的父结点为红色,这时就需要进行一系列操作以保证整棵树红黑性质。如下图所示,由于父结点为红色,此时可以判定,祖父结点必定为黑色。这时需要根据叔父结点的颜色来决定做什么样的操作。青色结点表示颜色未知。由于有可能需要根结点到新点的路径上进行多次旋转操作,而每次进行不平衡判断的起始点(我们可将其视为新点)都不一样。所以我们在此使用一个蓝色箭头指向这个起始点,并称之为判定点。
2.1 红叔
当叔父结点为红色时,如下图所示,无需进行旋转操作,只要将父和叔结点变为黑色,将祖父结点变为红色即可???不可以为黑色吗?。但由于祖父结点的父结点有可能为红色,从而违反红黑树性质。此时必须将祖父结点作为新的判定点继续向上(迭代)进行平衡操作。
需要注意的是,无论“父节点”在“叔节点”的左边还是右边,无论“新节点”是“父节点”的左孩子还是右孩子,它们的操作都是完全一样的(其实这种情况包括4种,只需调整颜色,不需要旋转树形)。
2.2 黑叔
当叔父结点为黑色时,需要进行旋转,以下图示了所有的旋转可能:
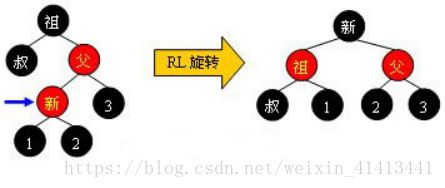
Case 1:新结点为外侧插入,叔为黑
先对父、祖做一次右旋转,并更改父、祖颜色.
注意结点3的去处,因为其比祖小比父大,故应放在祖的左结点处。
Case 2:新结点为内侧插入,叔为黑
先对父、新进行左旋转(2成为父的右子结点),再对祖 做右旋转
Case 3:新、父进行右旋转,之后祖、新进行左旋转
Case 4: 祖、父、新进行左旋转
可以观察到,当旋转完成后,新的旋转根全部为黑色,此时不需要再向上回溯进行平衡操作,
插入操作完成。需要注意,上面四张图的“叔”、“1”、“2”、“3”结点有可能为黑哨兵结点。
红黑树的数据结构
红黑树提供“遍历”操作以及iterators(迭代器)。
按正常规则(++ite)遍历,便能获得排序状态(sorted).
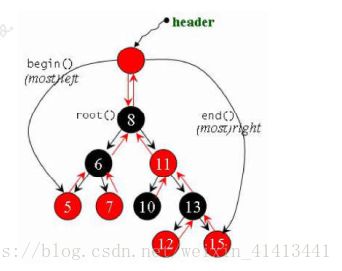
如上图所示STL为红黑树的根结点设计了一个父节点,名为header。初始化状态为:其左子结点和右子结点均为自己。,header的设计是为了实现上的方便,不是真正的元素。与list的空节点类似。
当有元素插入时,两者互为父节点。
红黑树维护着两个迭代器begin()和end(),begin()始终指向最左子节点,end()始终指向最右子节点。遍历的时候从begin()开始,end()结束。
我们不应使用红黑树的迭代器改变元素值(因为元素排列规则,红黑树是按照map的key排列的)。但编程层面是可以改的,因为红黑树即将为set和map服务,而map允许元素的data被改变,只有元素的key才是不可以被改变的。
红黑树的结点定义
RB-tree有红黑两色,并且拥有左右子节点,设计时将结点分为两层
typedef bool _rb_tree_color_type;
const _rb_tree_color_type _rb_tree_red=false;//红色为0
const _rb_tree_color_type _rb_tree_black=true;//黑色为1
Struct_rb_tree_node_base
{
typedef _rb_tree_color_type color_type;
typedef _rb_tree_node_base *base_ptr;
color_type color;//结点颜色,非红即黑
base_ptr parent;//红黑树的header
base_ptr left;//指向左结点
base_ptr right;//指向右结点
static base_ptr minimum(base_ptr x)
{
while(x->left!=0)
x=x->left;
return x;
}
static base_ptr maximum(base_ptr x)
{
while(x->right!=0)
x=x->right;
return x;
}
};
Template
struct _rb_tree_node:public _rb_tree_node_base
{
typedef _rb_tree_node* link_type;
Value value_field;//结点值
}; 面试时可以简答为:
enum Color
{
RED = 0,
BLACK = 1
};
struct RBTreeNode
{
struct RBTreeNode*left, *right, *parent;
int key;
int data;
Color color;
};
红黑树的构造函数
红黑树的构造有两种方式:1 以现有红黑树复制一个新的红黑树
2 产生一颗空的红黑树
rb_tree
红黑树的析构函数
析构函数负责清除和释放红黑树上的每一个节点,并且初始化该红黑树为空树,即恢复header为初始状态
红黑树提供两种insert操作:insert_union()和insert_equal().
返回值是一个RB-tree迭代器,指向新增结点
前者表示结点的key一定在整个tree中独一无二,否则安插失败;后者表示结点的key可重复。
RB-tree的find函数
//寻找红黑树中是否有键值为K的结点
rb_tree::find(const Key&k)
{
link_type y=header;//x的父节点
link_type x=root();//当前结点
while(x!=0)
if(!key_compare(key(x),k)//key_compare()是结点键值大小比较准则。
//x键值大于k,则向左走
y=x,x=left(x);
else x=right(x);
iterator j=iterator(y);
return (j=end()||key_compare(k,key(j.node)))?end():j;
} RB-tree的迭代器:
为了将RBtree实现为一个泛型容器,迭代器的设计很关键。
迭代器和节点一样,采用双层设计,STL红黑树的节点__rb_tree_node继承于__rb_tree_node_base;
STL的迭代器结构__rb_tree_iterator继承于__rb_tree_base_iterator。
其中有*、->、++(调用了基层increment())、--(调用了基层decrement())等迭代器操作算子。
RB-tree的迭代器是双向迭代器,但是不能随机访问。