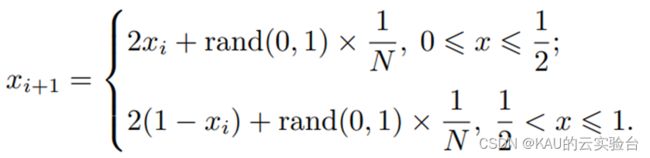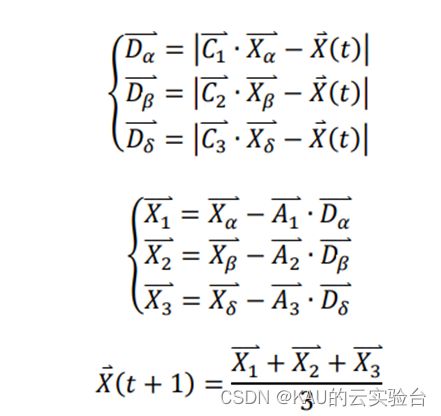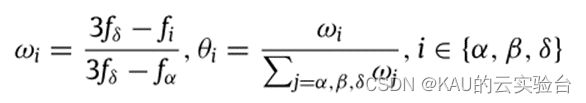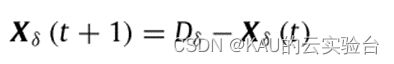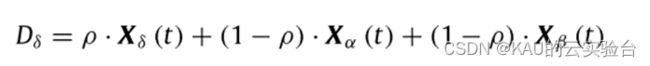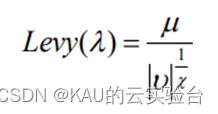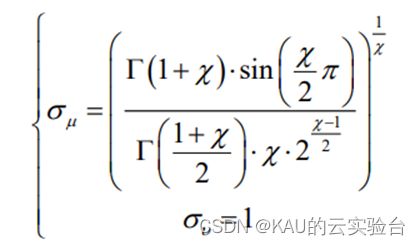性能优越!|融合多策略的灰狼优化算法
灰狼优化算法是Mirjalili等于2014年提出的一种新型SI算法,GWO通过模拟灰狼群体捕食行为,基于狼群群体协作的机制来达到优化的目的,这一机制在平衡探索和开发方面取得了不错的效果,并且在收敛速度和求解精度上都有良好的性能,目前已广泛应用于工程领域,如:神经网络、调度、控制、电力系统等。
然而GWO也存在早熟收敛的缺点,并且容易停滞在局部最优解。为解决该问题,有几类改进方向可以参考:
(1)调整控制参数
(2)引入新的搜索策略
(3)与其他优化算法混合
(4)修改狼群结构
基于以上思想,本文设计出融合多策略的灰狼优化算法,函数测试结果显示,改进的算法性能得到明显提升。
00 文章目录
1 灰狼优化算法原理
2 改进的灰狼优化算法
3 代码目录
4 算法性能
5 源码获取
6 总结
01 灰狼优化算法原理
灰狼优化算法原理及其MATLAB代码获取方式在前面的文章中已经介绍 ,这里不再阐述
02 改进的灰狼优化算法
2.1 改进的Tent混沌初始化
群体的算法的初始化影响其搜索性能。由于没有先验信息,个体通常是由随机初始化产生的。这种策略在某种意义上是有用的。但是,有时候个体在搜索域中的分布并不均匀,这可能会使个体远离全局最优解,导致收敛速度较低。
混沌具有遍历性、随机性和规律性等特征,是非线性系统中的一种普遍现象,利用混沌变量搜索显然比无序随机搜索具有更大的优越性。目前文献中常用的混沌扰动方程有Logistic映射和Tent映射等。由文献[3]可知Logistic映射的分布特点是:中间取值概率比较均匀,但在两端概率特别高,因此当全局最优点不在设计变量空间的两端时,对寻找最优点是不利的。而Tent混沌映射结构简单,具有比Logistic混沌映射更好的遍历均匀性和更快的搜索速度,但 Tent映射迭代序列中存在小周期, 还存在不稳定周期点, 为避免Tent混沌序列在迭代时落入小周期点和不稳定周期点,在原有的Tent 混沌映射表达式上引入一个随机变量rand(0, 1) × 1 /N[1]。则改进后的Tent混沌映射表达式如下:
其中: N 是序列内粒子的个数。引入随机变量rand(0, 1) /N ,不仅仍然保持了Tent混沌映射的随机性、遍历性、规律性,而且能够有效避免迭代落入小周期点和不稳定周期点内。本文算法引入的随机变量,既保持了随机性, 又将随机值控制在一定的范围之内,保证了Tent混沌 的规律性。

图显示了Logistic、Tent和改进的Tent混沌映射产生的混沌序列在二维区域中的初始分布,可以观察到,改进后的Tent混沌映射的分布均匀性较好,因此本文以改进Tent混沌性来代替麻雀搜索算法的随机初始化,以提高和改善初始种群在搜索空间上的分布质量,加强其全局搜索能力,从而提高算法求解精度。
2.2 自适应狩猎权重系数
GWO和其他SI算法之间的主要区别是其社会领导层次结构,这能够对GWO搜索能力的提高有相当的价值。等级越高的灰狼,对猎物的了解就越深,领导能力也就越强,这种关系在搜寻过程中对群体狩猎起着至关重要的作用。然而在原始GWO的狩猎中(见下式),三个头狼的权重系数相同,这显然与真实狼群的等级制度矛盾。
受引力搜索算法中的质量更新公式的启发,引入下式来衡量三个领头狼的重要度:
θi即为各头狼对应权重。式中,头狼离猎物(最优)越近,则权重越高,α狼为灰狼群落提供了主要的运动方向,而β狼和δ狼则提供了辅助方向,以加快对猎物的包围和攻击。
2.3 改进控制参数a
GWO中的参数a控制勘探和开发过程,其主要影响A的值,当 | A | >1 时,灰狼群体将扩大包围圈,以寻找更好的猎物,此时对应于全局搜索(勘探); 当| A | < 1 时,灰狼群体将收缩包围圈,以对猎物完成最后的攻击行为,此时对应于局部精确搜索(开发)。
参数a的变化是从勘探到开发过渡的控制因素,灰狼在自然界中的狩猎过程是复杂的,因此简单的线性变化不能有效的表征其搜索过程。本文使用正弦形式的a的变化来改进线性的搜索过程,其表达式如下:

其中,t表示当前迭代数,max_iter表示最大迭代数。
下图中展示了该非线性函数和标准GWO中的线性函数的比较。由图可知,本文的非线性函数在迭代初期,a的取值更广,其可用于勘探的范围也更广;而在迭代后期,a较小,有助于算法进行局部开发,加快其收敛速度。
2.4 改进的头狼位置更新方式
α、β和δ狼代表着GWO中种群的进化方向,对于搜索方向上的指导上发挥着至关重要的作用。然而,在传统GWO中所有灰狼的位置更新依赖于相同的机制,没有考虑到头狼的特殊地位,并且按照实际情况来看,灰狼个体只接受等级更高的狼的引导,然而在算法中α、β和δ狼也会受比其地位更低的狼的领导,这并不合理。此外,GWO算法的搜索性能有限,因为当所有的狼都被头狼吸引到一起时,种群多样性迅速变差,此时 GWO将早熟收敛。为解决该问题,对α、β和δ狼分别采用单独的更新策略:
(1)δ狼
δ狼将接受α和β狼的领导,其更新方式如下:
其中ρ是分布在[0,1]中的随机数。随机数能使GWO在整个优化过程中表现更多随机性,有助于全局探索。
(2)β狼
β狼将接受α狼的领导,本文参考鲸鱼算法的螺旋更新机制,使其以螺旋运动接近α狼,其更新方式如下:
![]()
其中,ρ是分布在[0,1]中的随机数。随机数的引入同样是增强β狼的探索能力。
(3)α狼
α狼在狼群中等级最高,理应不受其他狼的引导,因此引入随机游走的策略来更新α狼。由于Levy 飞行机制具有短距离的探索性和长距离的跳跃性,短距离的探索性与偶尔的较长距离跳跃性偶然转换。短距离的探索性保证α狼在自身周围进行搜索,增加寻优的速度和准确性,偶尔的较长距离跳跃性可以扩展α狼搜索的区域,搜索更加广泛。
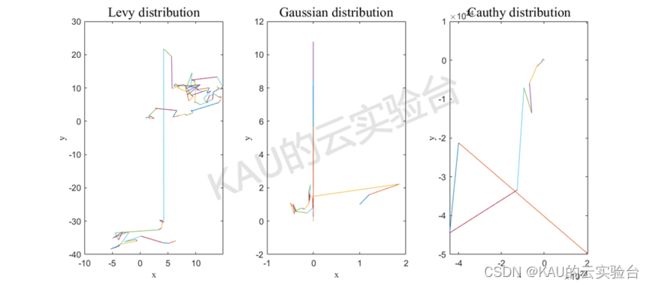
由图可知, Levy分布集成了高斯分布的小步长扰动和柯西分布大步长扰动的特点,因此能提高α狼的勘探和开发能力。同时,考虑到Levy机制存在随机性,因此借鉴“贪婪”选择思想,实现优胜劣汰的选择机制。引入Levy飞行机制:
![]()
Levy(λ)为随机搜索路径,➕代表点乘,α为步长控制因子,一般取0.01。
由于莱维分布十分复杂,无法实现,目前常用 Mantegna 算法模拟其飞行轨迹,其数学表达式如式所示:
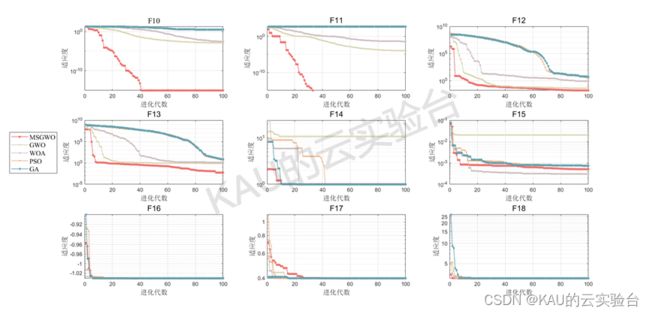
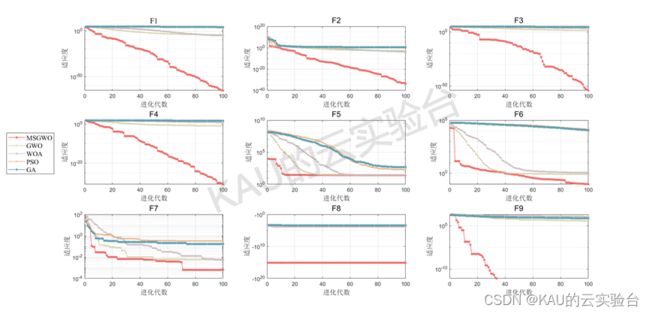
其中,参数c与Levy (l ) ~t^-l中的 l关系为 l=1+ c,且 0 式中,G为伽马函数,常数c一般取1.5 其中,rand4 表示[0,1]间的随机变量,p 为优胜劣汰选择概率,f (⋅) 为个体的适应度值。从上式可知,采用该策略,可使种群朝着最优的方向进化,同时有效地提高算法的搜索效率。 其中,Main_MSGWO.m为主程序,代码注释详细,一键运行Main_MSGWO即可得到所有运行结果。 运行结果包括:混沌序列比较图、控制参数比较图、levy与高斯、柯西分布比较图以及算法在各测试函数上的迭代图,最后将生成excel表,包含算法在各函数迭代n次的平均值,均值、运行时间、最优解。同时,文件也有乱码解决,给出了主要代码的txt文件。 生成excel文件:(其中12345分别对应MSGWO、GWO、WOA、PSO、GA) 由结果可以看到,除了少数函数外,改进的灰狼优化算法在大部分函数的收敛速度和精度都更好,改进算法的效果良好。 可私信作者或关注作者公众号:KAU的云实验台 本文提出的改进灰狼优化算法具有良好的性能,改进有效,同时,本文的改进策略也可以进行推广,比如将灰狼算法的领头狼的机制引入其他算法中。对于本文的算法,也可以进一步改进,比如引入人工蜂群中的食物源的思想,若算法出现进化停滞,可以辅以扰动,想必也能进一步提升性能。 [1]张娜,赵泽丹,包晓安等.基于改进的Tent混沌万有引力搜索算法[J].控制与决策,2020,35(4):893-900. [2]Long, W., Jiao, J., Liang, X., & Tang, M. (2018). Inspired grey wolf optimizer for solving large-scale function optimization problems. Applied Mathematical Modelling, 60,112–126. [3]Miao,Zhaoming等.Grey wolf optimizer with an enhanced hierarchy and its application to the wireless sensor network coverage optimization problem[J].APPLIED SOFT COMPUTING,2020,96. 另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。 如果这篇文章对你有帮助或启发,可以点击右下角的赞/在看(ง•̀_•́)ง(不点也行) 03 代码目录
04 算法性能
05源码获取
06 总结
参考文献