计算机组成原理 new09 定点数的移位运算
文章目录
-
-
-
- 原码/正数反码/正数补码的算术移位
- 负数反码的算术移位
- 负数补码的算术移位
- 算术移位总结
- 符号扩展
- 算术移位的应用
- 真值的算术移位
- 逻辑移位
- 逻辑移位的运用
- 循环移位
-
- 不带进位位的循环移位(小循环)
- 带进位位的循环移位(大循环)
- 原码定点一位乘法
- 原码定点一位乘法(手算) (这里我说了两个符号位都是0对数值位不会产生影响,对于原码是适用的,补码的乘法还不知道,这里需要再斟酌一下)
- 补码定点一位乘法
- 原码除法(恢复余数法)
-
- 补码的除法运算
- C语言类型转换
- 大端和小端
- 边界对齐(内存对齐)
- 两种对齐方式的访存消耗
-
-
 #### 算术移位
#### 算术移位
算术移位:一般用于原码,反码,补码。
原码/正数反码/正数补码的算术移位
因为正数的原反补相同,所以正数的反码和补码和原码的算术移位规则相同。
在没有丢失有效数据的的情况下,原码的算术左移一位相当于将原码的真值x2,算术右移相当于将原码的真值/2,反码和补码也是如此。
( 1 ) (1) (1)算术右移
一次的正常的算术右移相当于对真值/2,但是如果算术右移低位丢弃的不是0,就会导致精度丢失,例如:
在这次算术右移中,低位丢失的为1,所以导致精度丢失,原本-5/2应该得到-2.5,但是因为精度丢失,结果变成了-2。

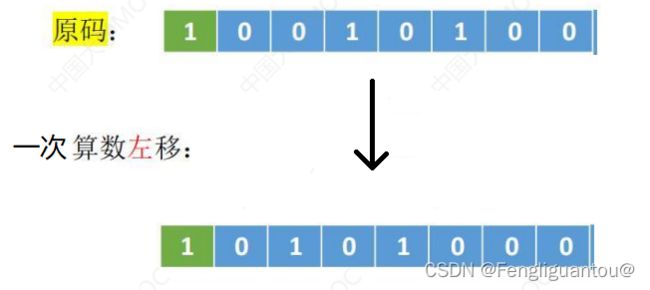
( 2 ) (2) (2)算术左移
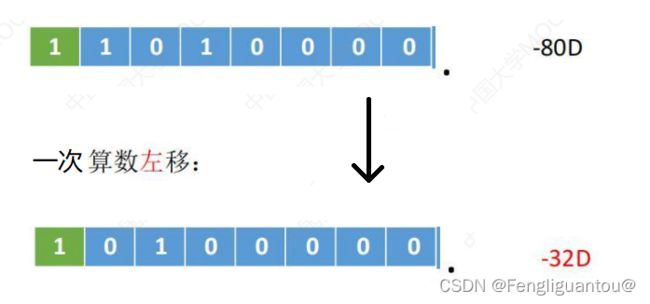
在算术左移过程中,丢失的是高权值位,所以如果高位丢失的是1,就会造成严重误差,例如:
这次算术左移过程中,高权值的1被丢弃,但是原本一次算术左移的真值应该是-160,因为高权值位的数据丢失,真值变成-32。
正数原码和负数原码的算术移位规则相同吗?
相同的,因为算术移位本质是对真值扩大2或者缩小2,正数原码和负数原码具有位权,所以规则是相同的。
负数反码的算术移位
首先,负数反码是由原码符号位不变,数值位按位取反得到的:
所以在负数反码中,负数反码的1本质上等于负数原码对应位置的0。
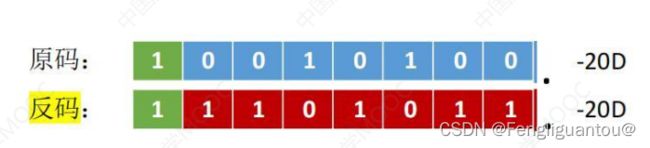
( 1 ) (1) (1)算术右移
规则:符号位不参与移动,高位补1,低位舍弃
算术右移时,若低位丢弃的不是1,则会造成精度损失,这很好理解,因为补码的1就是反码的0。
( 2 ) (2) (2)算术左移
规则:符号位不参与移动,高位舍弃,低位补1
算术左移时,如果高位丢弃的不是1,就会造成严重的误差。
负数补码的算术移位
首先回忆下,负数反码是如何转负数补码的:
从左到右找到第一个0,将这个0和这个0右侧的所有位全部取反。
可以看出,通过反码转原码的方法,可以将补码转成两个部分,补码第一1和这个1右侧的所有位和原码相同,这个1左侧的数值位和反码相同。
( 1 ) (1) (1)算术右移
规则:高位补1,低位舍弃
负数的补码在右移时,低位丢1,会造成精度的损失。
( 2 ) (2) (2)算术左移
规则:高位舍弃,低位补0
负数的补码在左移时,高位丢0,会产生巨大误差。
算术移位总结
为何正数原码和反码的移位都是补0
因为正数原码和反码的数值位具有权重。
符号扩展
我们先回到算术移位中,在原码的时候,为什么我们算术移位的时候都是补的0,因为无论是正数的原码还是反码,我们补进来的0,只会对数据的位置发生影响,即只会改变原数据的权重,例如00110,其中两个1的权重是2和4,我们进行一次左移,就会变成
01100,这时候我们在最低位补了0,但是我们补进来的0不会对让数据加上这个位上的数字,因为原码中0是无效的。所以我们原码就是进行补0
而负数反码是原码取反,所以为了使反码中补的数字也是无效的,所以反码我们需要补1
在负数补码中,数据被分成了反码和原码,所以同样是为了保持补进来数据的无效性,所以我们原码部分补0,反码部分补1。
我们分为有符号整数的扩展和有符号小数的扩展:
( 1 ) (1) (1)有符号整数(纯整数)的扩展
首先我们要知道,整数的扩展补的是高位,因为我们是纯整数。
在明白了上述以后,我们开始看向位数的扩展:
首先,我们需要知道位数扩展的本质是让位数变多,但是不影响原有数据的值,即扩展的都应该是当前状态下的无效位。
正数(正数原反补)的扩展:
假设需要扩展到n位,那么将符号位移动到第n位,然后在中间补0。
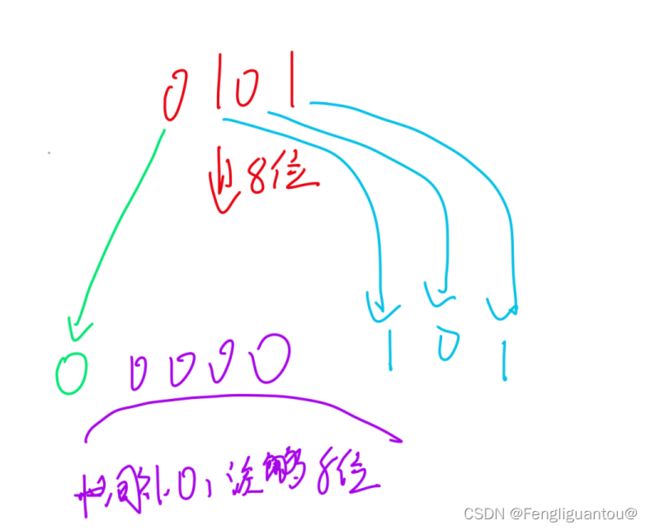
原码负数也是如此:先将符号位移动到扩展以后的最高位,然后中间补0。

负数反码:负数反码,因为反码的最高位已经是1了,然后中间补的又是1,所以我们可以省去符号位移动的步骤,直接在前面补1。
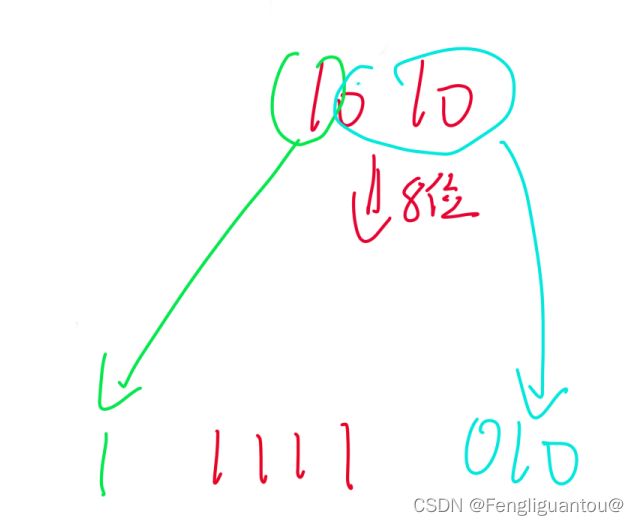
负数补码:和负数反码相同,可以省去符号位的移动,直接在前面补1即可。
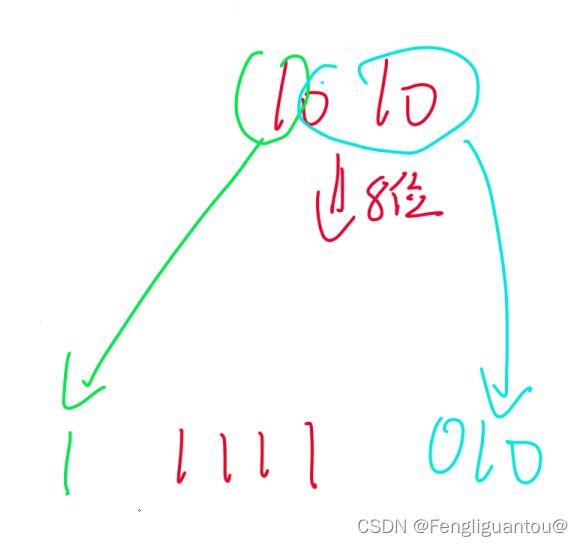
( 2 ) (2) (2)有符号小数(纯小数)的扩展
在小数中,我们补的是低位,因为我们是纯小数,所以我们只会往低位补位。补位的要求照样是相同的,补进来的是无效位。
对于正数(原反补)来说:
我们都是在最低位补0,负数原码也是如此
对于负数反码来说我们在末尾补1
而对于负数补码而言,因为右边同原码,所以我们末尾补0。
( 3 ) (3) (3)无符号数的扩展
无符号数扩展时,高位补0即可。
算术移位的应用
通过算术移位和加法的搭配使用,可以完成乘除法的运算:
( 1 ) (1) (1)乘法
1.乘上一个正数
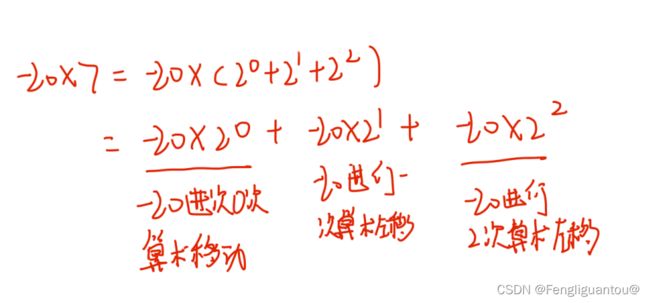
2.乘上一个负数(这里就有点问题了)
真值的算术移位
实际上我们得到的真值可能是带有小数和整数的,因为真值没有位数的限制,如果题目没有说要将真值存储在某个寄存器时,对其算术移动时,我们只需要移就好了,真值就没有什么算术左移和右移,就是直接移动就完事了。

逻辑移位
逻辑移位很简单,可以看作是对无符号数的移位,其每次移动是对所有二进制位的移动。
逻辑右移:高位补0,低位舍弃
逻辑左移:高位舍弃,低位补0
逻辑移位都是补0。
逻辑移位的运用
假设现在要将102,139,139这三个数字连接在一起,这时候就可以使用逻辑移位,通过逻辑移位将对应的二进制数字移动到对应的位置,最后将三个移动后的数字进行相加即可。

除此以外,循环移位还能完成数据的交换,例如1234通过循环移位以后可以变成4321
循环移位
循环移位分为不带进位位的循环移位和带进位位的循环移位,
两者的移位都是对所有二进制位的移动。
不带进位位的循环移位(小循环)
不带进位位不是说没有进位,而是说进位不一起参与循环移位。
( 1 ) (1) (1)循环左移
规则:将最高位多出来的位,补到最低位,并且将这位覆盖到进位内。
( 2 ) (2) (2)循环右移
将最低位多出来的位,补到最高位,并且将多出的位覆盖到进位内
带进位位的循环移位(大循环)
带进位位的循环移位和普通的循环移位相同,其只是多了一个CF进位标志,移位规则就是将这个CF一同参于移位,将CF看作是最高位。
CF的初值题目会给出。
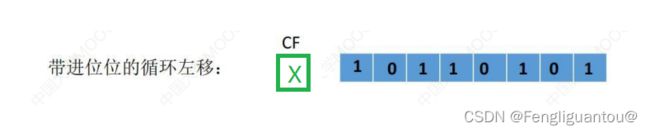
( 1 ) (1) (1)循环左移
规则:将最高位多出来的位,补到最低位。
( 2 ) (2) (2)循环右移
将最低位多出来的位,补到最高位
原码定点一位乘法
在说明如何进行一位乘法之前,我们先看下我们小学时候学过的乘法:
进行小学乘法的时候,我们每次都是让乘数的一个数位乘上被乘数得到该位的乘积,最后将乘数所有数值位的乘积相加得到结果,其中有一个需要注意的点是,在进行乘积相加的时候我们每次都会进行一个错位。这种每次计算一位乘积的就是一位乘法。
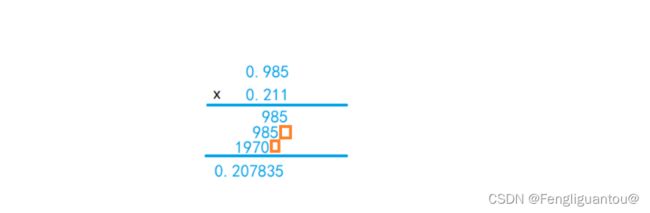
实际上,我们在计算二进制乘法的时候也是使用的十进制乘法的方式。

但是有个问题,我们在进行小学乘法的时候,都是正数x正数,如何其中有负数的时候要如何解决?
在计算机中,对于乘法的符号位进行了单独的处理,符号位=被乘数的符号位^乘数的符号位。
对于计算机中的乘法运算我们只需要记住一点:本质上就是模拟二进制的乘法运算。
( 1 ) (1) (1)定点小数的一位乘法运算
具体的实现原理我们开始进行一次操作:
第一步:
将
ACC置0,将被乘数和乘数全部取绝对值(即符号位都改为0)。在X内填入被乘数,MQ内填入乘数。
第二步:取乘数的最低位进行判断,如果是0,就让ACC+0(加0其实就是不变),如果是1,就让ACC加上被乘数。
第三步:让ALU和MQ整体逻辑右移,ACC顺位移动到MQ内部,MQ的低位舍弃,ACC高位补0。
然后再返回第一步,以此类推,直到MQ的最后一位是乘数取绝对值以后的符号位,即0。
即假设小数,例如上图中的小数在小数位有4位,那么就需要4次的运算和移位。
最后,当计算机侦测到计算到乘数取绝对值的符号位以后,停止计算。取乘数和被乘数没有取绝对值以前的符号位进行异或,根据异或的结果替换
ACC的最高位。最终完成这个操作以后,ACC的所有位+MQ去掉最后一位就是原乘数和被乘数相乘的结果。
注意:最后得到的结果,要将MQ的最后一位去掉,因为MQ的最后一位是符号位。
现在对于这个过程我们回答几个细节问题:
逻辑移位发生在什么时候?
首先我们回想我们进行十进制乘法的时候,我们得出第一次的位积的时候,我们是不用进行错位的,当我们从第二位的位积才开始需要进行错位,所以在计算机中也是如此,进行第一位的运算前,不进行逻辑右移。每当执行完一次乘积运算,即进行一次逻辑右移。假设乘数有
n+1位,数值位有n位,我们就需要进行n次的乘积运算,即n次的逻辑右移。
为什么进行完最后一位数值位的乘积运算以后,还需要进行逻辑右移?
因为在计算机中是通过判断当前位是否是乘数取绝对值以后的符号位,从而来判断乘法运算是否结束的,所以进行完最后一位数值位的乘积运算以后,进行一次逻辑右移,那么下次进行乘积运算的就应该是符号位,计算机检测到符号位,就停止计算。
原码的定点一位乘法中,乘数的符号位有没有参与运算?
没有参与运算,其只是作为计算机判断数值位计算结束的一个标志。
为什么被乘数的符号位也参与了运算?
首先,我们在进行运算之前,对被乘数和乘数的符号位取了绝对值,所以说被乘数和乘数在参与计算的时候,两者的符号位都是
0。所以MQ的最高位一直保持是0,无论乘数当前的位是0是1,填入ACC最高位的一定是0,所以虽然说符号位好像参与了运算,但是因为是0,所以对数值位的结果不造成影响的,只需要在最后的时候,对ACC的高位进行符号位修正即可。
现在我们返回来看这个计算过程,在整个计算过程中,MQ存储的是乘积低位,ACC存储的是乘积的高位,X存储的是被乘数。这里的乘积低位和乘积高位如何理解?
这里说的乘积高位和乘积低位指的是运算以后的结果,
MQ存储的是运算结果的低位,ACC存储的是高位。
对于上述的细节我们还需要进行补充:
我们在进行上述乘法运算过程中,每次都会进行逻辑右移操作,ACC会顺位移到MQ中,我们将ACC里的所有位和ACC移动到MQ里的位叫做部分积。这很好理解,部分积就是部分乘积的和。
原码定点一位乘法(手算) (这里我说了两个符号位都是0对数值位不会产生影响,对于原码是适用的,补码的乘法还不知道,这里需要再斟酌一下)
同样的,我们可以使用手算的方式来模拟计算机中,对于定点数的乘法运算。
其本质过程和机器相同。只不过这里我们采用了双符号位,但是实际上双符号位和单符号位对于运算没有影响,因为我们对乘数和被乘数都取了绝对值,所以即使有两个符号位,也是两个0,不会对数值位的运算产生影响。
下面的手算图中,我们会发现
MQ中没有表明符号位,实际上这个是不影响的,因为是手算,我们只要将乘数的所有数值位都参与了乘积运算即可停止,最后得到的运算答案也是要舍弃掉乘数的符号位的,所以说不影响。
注意:一开始加0是因为一开始要将ACC清零。
( 2 ) (2) (2)定点整数的一位乘法运算
定点整数的乘法运算也是一样的步骤,只是对于运算结果的解释方式不同,无论是定点整数还是定点小数,最后得到的结果中,最高位都是符号位,只不过定点小数的小数点在符号位后,定点整数的小数点在答案末尾。
补码定点一位乘法
补码的定义一位乘法中,大致思路和原码相似,但是仍然存在一些区别:
现在我们介绍一次计算机中完整的补码乘法:
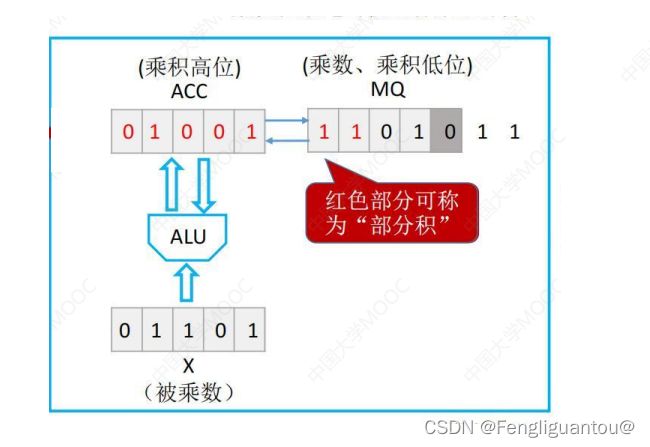
我们先看向补码乘法的一个框架:
假设是n位(包含符号位)的补码运算,需要n+1位的寄存器,下图中的x和y都是五位,所以需要的ACC,MQ,X都是6位。在MQ中我们设置了一个辅助位,在ACC和X中,设置了两个符号位用于表示符号信息。正数就是两个0,负数就是两个1,因为MQ使用了一个辅助位,所以其只有一个符号位。这里需要注意的是,实际上辅助位是MQ的最低位,但是因为接下来的运算需要使用到MQ和次低位和辅助位,所以这里我们修改下说法,将MQ的次低位叫成MQ的最低位,辅助位就是辅助位。(但是实际上我们心里是要清楚,辅助位其实是MQ的最低位),并且辅助位一开始的初值被设置为0。
注意:补码乘法中是算术右移,其在ACC的两个符号位不动,然后顺次移动到MQ内部,其在ACC高位缺出来的一位,如果是正数补0,负数补1。这里需要非常注意,虽然MQ也有符号位,但是这里MQ是整体移动一位的。
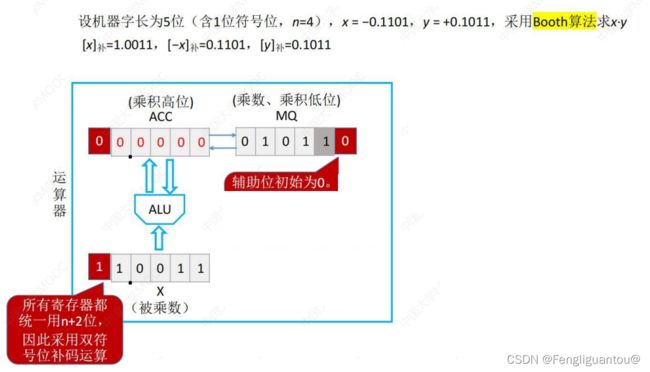
现在我们开始介绍如何运算,在补码的运算中,被乘数和乘数不需要取绝对值,两者的符号位可以直接参与运算,并且最后得到的结果也不需要对符号位进行修正。
所以我们就开始判断ACC需要加上什么数:
我们使用辅助位-MQ最低位来判断,当前ACC需要加上什么数据。
在加上数据以后,我们需要对ACC进行一次算术右移。
以此类推重复上述的步骤,直到我们开始执行乘数中符号位的位积,重点来了,计算完乘数中符号位的位积以后,我们不需要进行移位,也就是说算完乘数符号位的位积以后得到的结果就是乘法的答案,我们答案是ACC的所有位+MQ中的所有位除了辅助位。

最终我们得到答案:
一定要记住,我们的答案是

注意,无论时原码乘法还是补码乘法,最后的结果中的最后一位都是要去掉的。

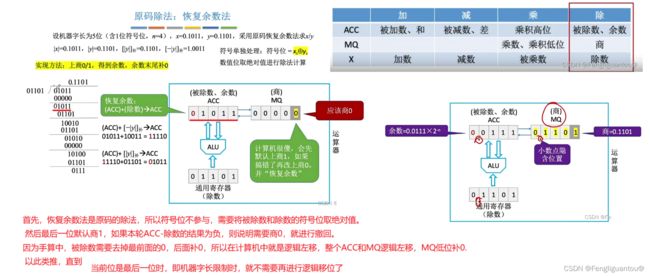
原码除法(恢复余数法)
首先,我们将被除数和除数扩大相同的倍数。
第一次商0,因为被除数小于除数,然后得到相减的结果1011,然后补一个0变成10110,然后商1得到结果1001,然后补一个0。
也就是说每次相减得到结果都需要补一个0。
这里因为机器字长是5位,所以我们的结果只需要包含5位即可。剩余的余数就不需要继续往下算了。

因为是原码的除法,符号位没法进行处理,所以这里我们和原码的乘法一样,符号位最后处理,先对符号位取绝对值。
然后一开始将被除数填入ACC,除数填入X。

首先,计算机对于每次商,其都会默认商1,例如每次商1,那么就需要让ACC-去X,但是计算机中只能进行加法,所以就需要减去|X|的求补以后的结果,即-X。然后我们这里的x存储的是|y|,因为是正数,所以-|y|这个原码就等于|y|看作是补码时候的-|y|。
然后商减去除数以后,内部会进行检查,发现符号位为1,说明相减的结果是一个负数,所以其需要退回本次的操作。
所以退回操作就是让11110加上原来的除数,然后写回ACC。
然后

所以这样一来,我们就可以得到本轮相减的结果01011。
这时候在手算中,我们的做法就是将01011中最前面的0去掉,然后在01011后面补上一个0,变成10110,而在计算机中的做法就是将ACC和MQ统一逻辑左移。

于是经过本次逻辑左移我们就可以得到:
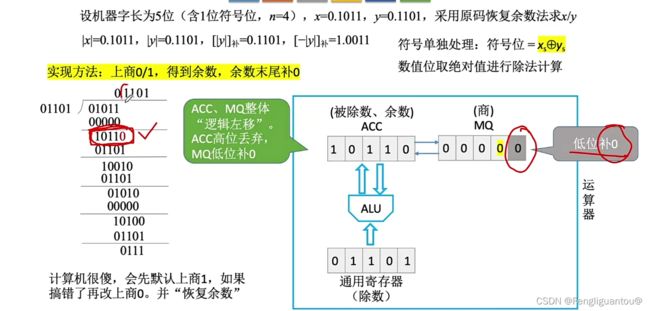
接下来下一步同样还是如此,使用MQ的最后一位作为商,先判断商1是否可行,本次是可行的,所以商1:
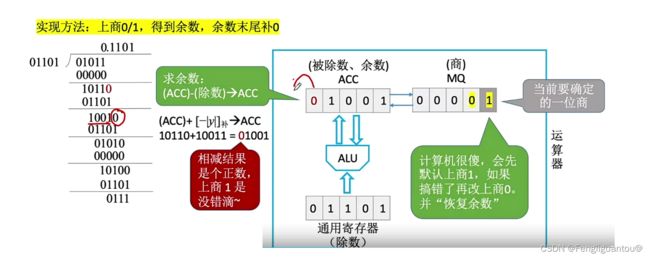
然后再进行一次逻辑左移:

这里需要注意的是,当我们进行最后一位商的时候,最后一次,即因为机器字长是5,所以最多商到第五位,所以第五位也就是最后一次商了,最后一次商完以后,是不会进行逻辑左移的。
其中最后ACC就是余数,我们的小数点是隐含在第一位后面的,但是余数还需要乘上2的-n次方。这里的n就为4,其小数位置的长度。

最后我们还需要对商的符号位进行一下修正,商最后的符号位取x和y的符号位相与以后的结果。

实际上恢复余数法我们可以进行一个优化:
如果本次商1失败,那说明其实本次其实就不需要商了,直接默认进行移位即可。
所以根据本次商0和下一次商中间的操作,实际上我们是可以跳过的。
也就是说如果本次商1失败,我们可以直接让ACC和MQ逻辑左移一位,然后加上除数。
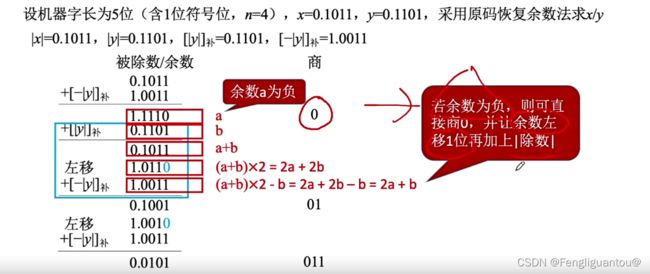
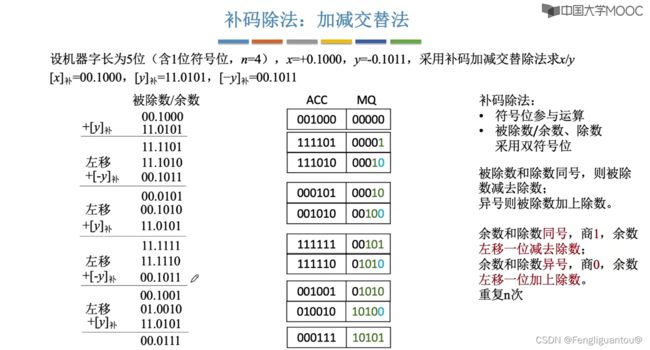
基于这个思想,我们就可以改进以后的原码除法,又叫做加减交替法,或者不恢复余数法:
即如果本轮商的结果是错误的,需要返回,就根据上面的方式直接跳到下一次商1,反之就正常商1:
但是需要注意的是,如果执行到最后一位商了,这时候如果本轮商是错误的,因为没有下一位商了,所以这时候就不能跳转了,而是应该进行恢复。
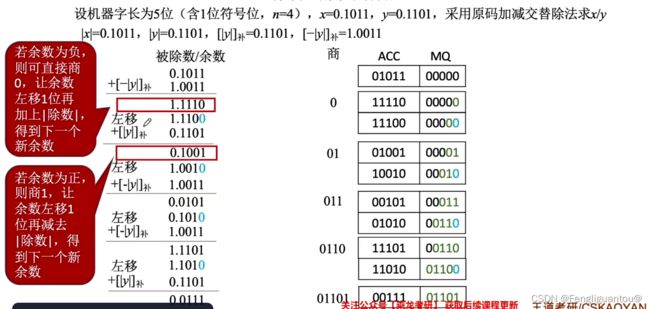
一共n+1位,所以商也是n+1位,所以需要加n+1次。但是如果最后一次出现错误,则需要加n+2次。

需要注意的是,在定点小数的除法中,得到的结果也必须是小数, 因为在计算机中小数和整数是不同的处理方式,其没办法同时处理,如果被除数大于除数,就会导致结果的第一位是1,即最后商的结果大于1,而定点小数是无法表示大于1的这个范围的。
所以也就是说定点小数的除法中,第一次肯定是商0,如果商1成功就代表除数大于被除数了,所以硬件就可以通过这个机制判断本次定点小数除法中,被除数和除数是否满足要求,如果第一轮商1,就说明有问题,其就会中止本次的除法操作。
补码的除法运算

对于补码除法的加减交替法和原码除法的加减交替法我们进行以下对比:
C语言类型转换
注意:数据类型的转换中,无论是强制还是隐式类型转换,或者是整形提升等等,都必须是补码级别的,也就是说必须先转换成补码,因为计算机存储的就是补码。
这里说的都是补码,计算机存储的本就也是补码。
( 1 ) (1) (1)相同长度有符号数和无符号数的转换
转换规则:直接拷贝,计算机只会改变对数字的解释方式。
例如:X的初值是1110 1111 0001 1111,因为x是有符号数,计算机就会使用有符号数的方式进行解释,对应真值就是-4321,将有符号数赋给无符号数的时候,是直接进行拷贝,只不过计算机解释无符号数的时候是以无符号数的方式。
这里无论是隐式类型转换还是强制类型转换都是如此。

( 2 ) (2) (2)长整数变短整数
无论是有符号/无符号长整数变有符号/无符号长整数都是相同的:
规则:直接高位截断。
例如int是32个bit,存储到unsigned short的时候会取int的最低16个bit拷贝到unsigned short。
( 3 ) (3) (3)短整数变长整数 (整形提升)
只需要知道一点,如果有强制类型转换,先进行强制类型转换,强制类型转换以后,再使用强制类型转换后的类型进行隐式类型转换。只有短整数到长整数需要整形提升。有符号的补符号位,无符号补0,char比较特殊是无符号,是进行补0。

大端和小端
大端存储:对于人类阅读比较友好,二进制在内存中存储和二进制本身的排序相同。
小端存储:适合计算机,因为计算机需要从低权值位开始读取。
最低有效字节(LSB):低权值位存储的数据
最高有效字节(MSB):高权值位存储的数据
例如二进制:00 11 22 33的高权值位就是00,低权值位就是11。
而在大小端中,高低权值位处于不同的位置:
大端中:低权值在高地址
小端中:低权值在低地址
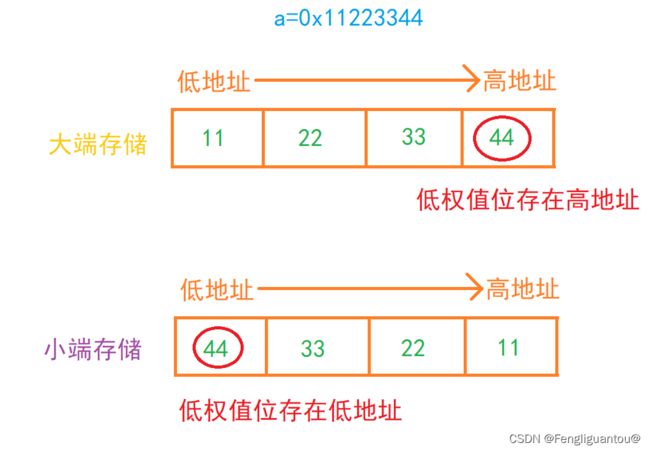
首先需要知道的是:内存中的地址都是按低到高的。虽然说有大小端之分,但是两者的存储区间都是相同的。
边界对齐(内存对齐)
首先我们要知道,现代计算机都是按字节进行编址的,按字节进行编址就是如下的:

什么是按字节编址,按字编址?
按字节的编址的意思是一个存储单元的大小是1个字节,按字编址的意思是一个存储单元的大小是一个字!
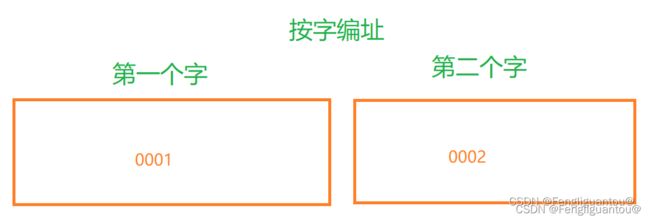
而计算机中的寻址方式有多种:
1.按字寻址
2.按半字寻址
3.按字节寻址
按字寻址我们可以理解为计算机根据字的大小对于内存进行了一种新的编址(实际上没有),也就是说假如一个字大小为4个字节,那么第0个字节就是第0个字,字地址为0,第5个字节就是第1个字,字地址为1。
按半字寻址也是如此,第0个字节就是第一个半字,半字地址为0,第3个字节就是第一个半字,半字地址为1。
按字节寻址就是普通的寻址方式。
从下图中我们可以看出在存储字长32bit的前提下:字地址,半字地址(实际上没有这两个玩意,为了便于理解)分别等于字节地址的4倍和2倍。所以我们根据字地址定位到某个字节的时候,需要将字地址x4转换成字节地址,半字地址也是如此,因为计算机中的x2就是逻辑左移,所以字转字节需要逻辑左移两次,半字转字节需要逻辑左移1次。

前面我们说了按字寻址,按字节寻址,按半字寻址,其最终都需要转成字节地址。而计算机每次访存的基本单位是一个存储单元,即一个字。例如我通过字节寻址定位到了第5个字节,那么计算机就会读取第5个字节所在的存储单元,即2号存储单元,这里需要非常注意,计算机读取的是所在的存储单元,而不是从第5个字节开始向后读取共4个字节。因为存储单元在主存中是一行一个,所以如果读1和存储单元的数据和2号存储单元的数据就需要两次访存。
因为计算机每次只能读取一个存储单元,所以计算机设计了两种关于内存的对齐方式:
( 1 ) (1) (1)边界对齐
边界对齐:当前存储单元如果能存的下就存,存不下就将剩余空间浪费,然后放到下一个存储单元存储。
例如计算机寻址到了第一个存储单元,然后想在这个存储单元存一个short,但是因为这个存储单元只剩一个字节了,存不下,所以计算机会放到下一个存储单元进行存储。
对于边界对齐还应该有更深刻的理解:
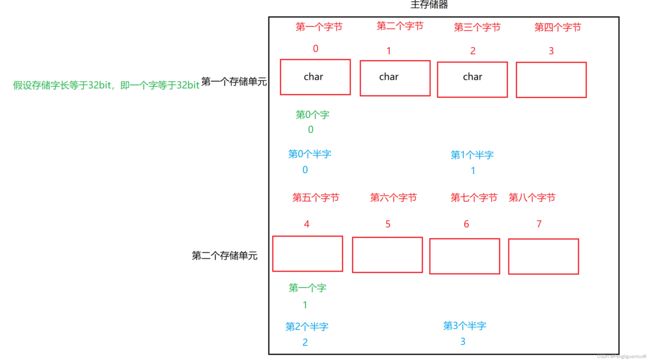
边界对齐本质上是要求:存储的地址要能够被数据的大小整除,例如下面的这道题:
虽然从0XC00D位置开始我们能够存入c这个数据,但是因为这个地址不是2的整数倍,所以我们不存这个位置,存0xC00E这个位置。

所以现在我们也就能够知道为什么在边界对齐中,无论是以字寻址还是半字寻址,只需要通过一次访问就可以取出数据,因为我们即对存储的地址做要求,还对存储单元做了要求,即必须存在一个存储单元内,并且开始存储的首地址需要被数据的大小整除。
( 2 ) (2) (2)边界不对齐
边界对齐:只要存储单元还有位置,就将数据存储进去,即使存的是数据的一半,三分之一等等
在边界不对齐中,想在1号存储单元存储一个short,因为只剩一个字节了,所以计算机就会存一半,将剩下一半放在下一个存储单元。
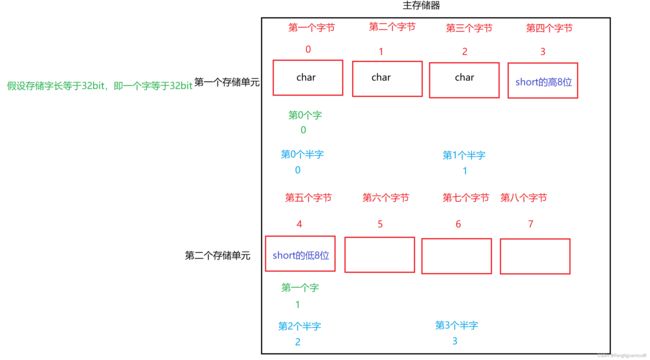
两种对齐方式的访存消耗
在边界对齐中,我们在存数据的时候可能会有存不下而造成空间的浪费,而在边界不对齐中不会造成空间的浪费。
但是当计算机想要将内存中的数据读取出来的时候,边界对齐和边界不对齐就会导致访存的次数不同:
在边界对齐中,访问一个字或者一个半字的数据肯定只需要一次访存,例如访问这里的short就只需要一次访存。
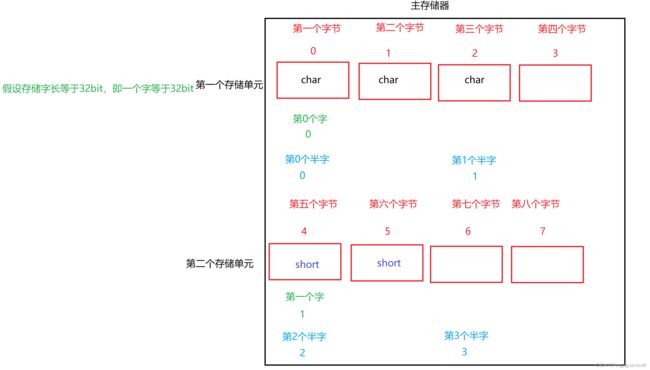
在边界不对齐中:
因为变量被分在了不同的存储单元,所以就可能需要两次访存。即计算机读取半字和一个字的数据的时候可能需要两次访存。
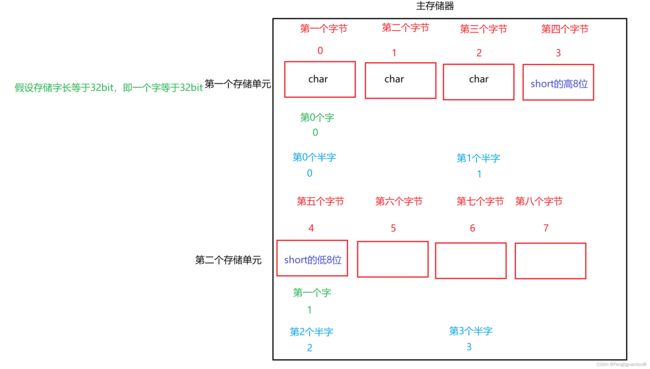
我们知道访存是很慢的,所以边界对齐方式实际上是一种空间换时间的操作。