剑指offer-寻找旋转数组中的最小值

第一种题型：数组没有重复的数字，即原数组是严格单调递增

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：
若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]
注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

示例 1：

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。
示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。
示例 3：

输入：nums = [11,13,15,17]
输出：11
解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。

题目解析

思路与算法

第一种：暴力解法，遍历数组找出最小值，时间复杂度为o(n)。

第二种解法：二分查找

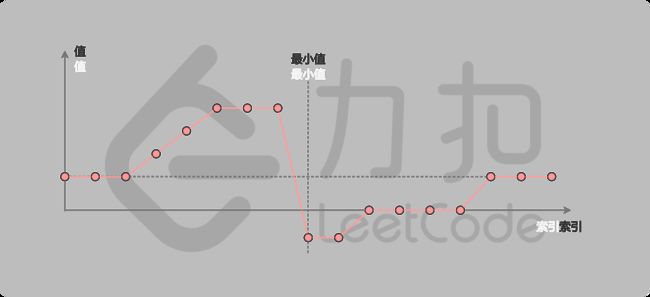
一个不包含重复元素的升序数组在经过旋转之后，可以得到下面可视化的折线图：

我们考虑数组中的最后一个元素 xx：在最小值右侧的元素（不包括最后一个元素本身），它们的值一定都严格小于 x；而在最小值左侧的元素，它们的值一定都严格大于 x。因此，我们可以根据这一条性质，通过二分查找的方法找出最小值。

在二分查找的每一步中，左边界为low，右边界为high，区间的中点为pivot，最小值就在该区间内。我们将中轴元素 nums[pivot] 与右边界元素 nums[high] 进行比较，可能会有以下的三种情况：

第一种情况是 nums[pivot]

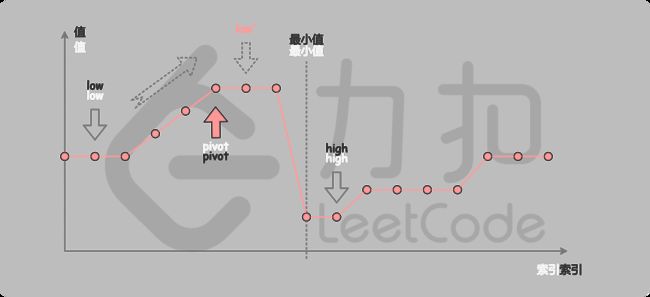
第二种情况是 nums[pivot]>nums[high]如下图所示，这说明 nums[pivot] 是最小值左侧的元素，因此我们可以忽略二分查找区间的左半部分。

由于数组不包含重复元素，并且只要当前的区间长度不为 1，pivot 就不会与high 重合；而如果当前的区间长度为 1，这说明我们已经可以结束二分查找了。因此不会存在nums[pivot]=nums[high] 的情况。

当二分查找结束时，我们就得到了最小值所在的位置。代码如下：时间复杂度为o(logn)，涉及到有序数组可以考虑作图的方法观察规律

 public int findMin(int[] nums) {
        int begin = 0;
        int end = nums.length-1;
        int mid = 0;
        while(begin < end) {
            mid = (begin + end) / 2;
            if(nums[mid] < nums[end]) {//如果右区间有序，则舍弃右区间
                end = mid;//这里end = mid而不是end = mid-1,这是因为右区间有序时，mid可能正好位于最小值的位置，所以如果end=mid-1可能会错过最小值
            } else {//如果左区间有序
                begin = mid+1;//根据图可以看出，如果区间[begin,mid]有序，则mid一定在最小值之前，故最小值在[mid+1,end]之间
            }
        }
        return nums[begin];
    }

 

 

对上述题目进行变形，如果数组中包含重复数字，即数组非递减，应该如何找出最小值？

第一种方法：暴力法，直接遍历，时间复杂度为o(n)

第二种：二分查找，需要上述思路做一下更改。

一个包含重复元素的升序数组在经过旋转之后，可以得到下面可视化的折线图：

我们考虑数组中的最后一个元素 x：在最小值右侧的元素，它们的值一定都小于等于 x；而在最小值左侧的元素，它们的值一定都大于等于 x。因此，我们可以根据这一条性质，通过二分查找的方法找出最小值。

在二分查找的每一步中，左边界为 low，右边界为high，区间的中点为pivot，最小值就在该区间内。我们将中轴元素nums[pivot] 与右边界元素 nums[high] 进行比较，可能会有以下的三种情况：

第一种情况是nums[pivot]

第二种情况是 nums[pivot]>nums[high]。如下图所示，这说明nums[pivot] 是最小值左侧的元素，因此我们可以忽略二分查找区间的左半部分，即让low = pivot+1;

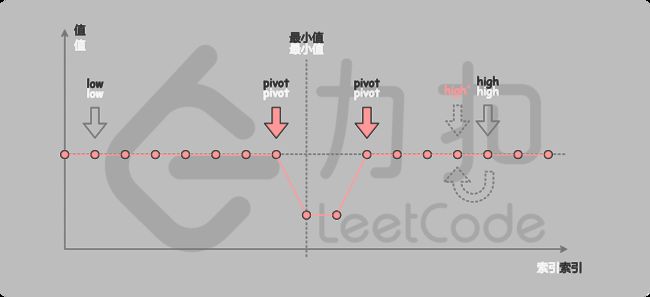
第三种情况是 nums[pivot]==nums[high]。如下图所示，由于重复元素的存在，我们并不能确定 nums[pivot] 究竟在最小值的左侧还是右侧，因此我们不能莽撞地忽略某一部分的元素。我们唯一可以知道的是，由于它们的值相同，所以无论nums[high] 是不是最小值，都有一个它的替代品nums[pivot]，因此我们可以忽略二分查找区间的右端点。

当二分查找结束时，我们就得到了最小值所在的位置，代码如下,时间复杂度为o(logn)

  public int findMin(int[] nums) {
        int low = 0;
        int high = nums.length - 1;
        while (low < high) {
            int pivot = low + (high - low) / 2;
            if (nums[pivot] < nums[high]) {
                high = pivot;
            } else if (nums[pivot] > nums[high]) {
                low = pivot + 1;
            } else {
                high -= 1;
            }
        }
        return nums[low];
    }

一般有如下情况：

如果是low<=high,则有low = mid+1,high = mid-1;

如果是low