LeetCode刷题总结C++-数组篇(下)
LeetCode刷题总结C++-数组篇(下)
本期讲O(n)类型问题,共14题。3道简单题,9道中等题,2道困难题。数组篇共归纳总结了50题,本篇是数组篇的最后一篇。其他三个篇章可参考:
- LeetCode刷题总结C++-数组篇(上),子数组问题(共17题)
- LeetCode刷题总结C++-数组篇(中),矩阵问题(共12题)
本系列50道题是作者在LeetCode题库数组标签中包含的202道题中,按照解答考点分类归纳总结的题型。解法仅供参考,主要在于题目和考点的分类。希望对准备刷LeetCode,而感觉题目繁多、标签太多、时间较少,不知道从何开始刷题的同学一点小小的帮助^~^,也是自己后期二刷的资料吧(PS:如果有时间的话)。
O(n)类型问题,是指要求算法的时间复杂度为O(n)。这类题目的特点是题意一般比较容易理解,而且其暴力求解的方案也比较容易想到。但是,题目确要求你不能采用暴力法求解,这往往是考察我们对双指针、快慢指针、动态规划、哈希数组和特定数学思想的应用。
在双指针方面,一般基础的策略是采用空间换取时间的策略。即先采用一个数组从原数组右边开始遍历,保存当前更新的临时变量。最后,从数组的左边开始依次遍历,不断更新最终的结果。此思路的应用,可以参考例9、例10和例11。
另外,双指针的应用解法也可以在O(1)的空间复杂度里面实现,采用一个临时变量随着遍历不断更新当前状态,夹杂着动态规划的思想。这类考点的应用,可以参考例5和例12。
在数学思维考察方面,组合数学的知识应用也是比较常见。比如考察对组合数学中字典序求解的应用,可以参考例1。数学中正负数转换为数组下标的思想,可以参考例2、例6。快速找到当前示例的数学规律,归纳出递推公式,可以参考例8、例13。
例3是一道非常经典的面试题,题目有多种解法,本文中给出是采用三次翻转求得最终结果的解法。在矩阵应用中,利用翻转操作一般也可以取得令人惊奇的效果。活用翻转也是一种技巧。
例4则是让人感叹的解法。采用摩尔投票法寻找数组中最多的元素。该思维应该可以归纳为寻找最多元素的一种特解思路。
在数组哈希思路的应用方面,可以参考例7和例14,是很典型的以空间换取时间的例题。
例1 下一个排列
题号:31,难度:中等
题目描述:
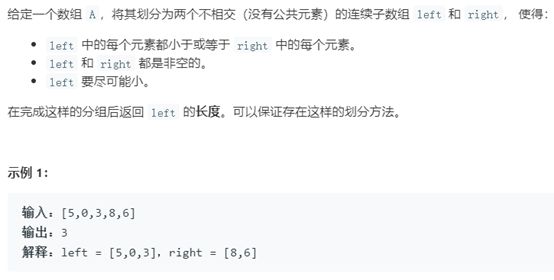
解题思路:
本题需要注意的关键点:原地修改,字典序。此题的解答用到了组合数学的知识,寻找比当前序列大的最小字典序。即从该序列尾部开始遍历,直到当前元素(假设位置为i)比该元素前面的元素大的时候停止。然后从i道最后一个元素序列中找到比第i-1个元素大的最小元素进行交换,最后把最后i个元素从小到大排序即可。
具体代码:
class Solution {
public:
void nextPermutation(vector& nums) {
int pos = nums.size() - 1;
while (pos > 0 && nums[pos] <= nums[pos - 1])
pos--;
reverse(nums.begin() + pos, nums.end()); //逆序
if (pos > 0){
int start = pos;
for (; start < nums.size(); start++){ //寻找第一个大于nums[pos - 1]的数
if (nums[start] > nums[pos - 1]){
swap(nums[start], nums[pos - 1]); //交换
break;
}
}
}
}
};
执行结果:
例2 缺失的第一个正数
题号:41,难度:困难
题目描述:
解题思路:
此题虽然被划分为困难题,实际上比较简单。题目要求是没有出现的最小正整数,那么返回的结果最大值只能是数组长度加1,最小值是1。那么只需要利用原有数组,把其中小于等于0的数字标记为大于数组长度*2的元素,剩下的把在1到数组长度之间的元素采用数组的下标元素取负数表示。最后,从数组第一个元素开始遍历,一旦出现大于0的元素,那么该元素下标即为最终结果。
具体代码:
class Solution {
public:
int firstMissingPositive(vector& nums) {
int n = nums.size();
for (int i = 0; i < n; ++i) {
while (nums[i] > 0 && nums[i] <= n && nums[nums[i] - 1] != nums[i]) {
swap(nums[nums[i] - 1], nums[i]);
}
}
for (int i = 0; i < n; ++i) {
if (nums[i] != i + 1) {
return i + 1;
}
}
return n + 1;
}
};
执行结果:
例3 旋转数组
题号:189,难度:简单
题目描述:
解题思路:
采用三次翻转操作。第一次将整个数组翻转一次,第二次将要右移的前K个元素翻转一次,第三次将剩余的k-n-1个元素翻转一次。最终得到的结构即为目标值。
具体代码:
class Solution {
public:
void rotate(vector& nums, int k) { // #include
reverse(nums.begin(), nums.end() - k % nums.size());
reverse(nums.end() - k % nums.size(), nums.end());
reverse(nums.begin(), nums.end());
}
};
执行结果:
例4 求众数II
题号:229,难度:中等
题目描述:
解题思路:
采用摩尔投票法,具体就是遇到相等的数,统计该数的个数自动加1,否则自动减一,一旦减到0后,更换当前存储的数字。摩尔投票法首次运用的题是求一维数组中数目超过一半的数(具体可参考题目:求众数, 题号169, 难度:简单)。本题稍作变换即可,开启两个变量计数和存储当前的数。开启两个数的数学意义在于,一个数组最多只能有两个数超过数组的三分之一。
具体代码:
class Solution {
public:
vector majorityElement(vector& nums) {
int n = nums.size();
vector result; //摩尔投票法
int count1 = 0, temp1 = 0;
int count2 = 0, temp2 = 0;
for(int i = 0;i < n;i++) {
if((count1 == 0 || temp1 == nums[i]) && temp2 != nums[i]) {
count1++;
temp1 = nums[i];
} else if(count2 == 0 || temp2 == nums[i]) {
count2++;
temp2 = nums[i];
} else{
count1--;
count2--;
}
}
count1 = 0;
count2 = 0;
for(int i = 0;i < n;i++) {
if(nums[i] == temp1)
count1++;
else if(nums[i] == temp2)
count2++;
}
if(count1 > n / 3)
result.push_back(temp1);
if(temp1 != temp2 && count2 > n / 3)
result.push_back(temp2);
return result;
}
};
执行结果:
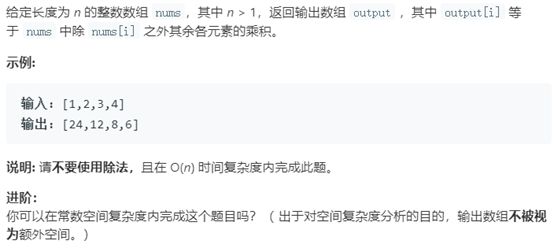
例5 除自身以外数组的乘积
题号:238,难度:中等
题目描述:
解题思路:
以空间换时间的策略,从数组左边依次遍历,保存连续乘积;然后,从数组右边依次遍历,保存连续乘积。最后,从数组第一数字开始遍历,取该数组左边的连续乘积和右边的连续乘积相乘即可。时间复杂度为O(n),空间复杂度为O(n)。
进阶如何使得空间复杂度为O(1)呢?即采用常数空间保存左边连续乘积,和右边连续乘积即可。这里感觉采用了动态规划的思路来临时保存左右连续乘积。
具体代码:
class Solution {
public:
vector productExceptSelf(vector& nums) {
vector result(nums.size());
int left = 1;
int right = 1;
for(int i = 0;i < nums.size();i++) {
result[i] = left;
left *= nums[i];
}
for(int i = nums.size() - 1;i >= 0;i--) {
result[i] *= right;
right *= nums[i];
}
return result;
}
};
执行结果:
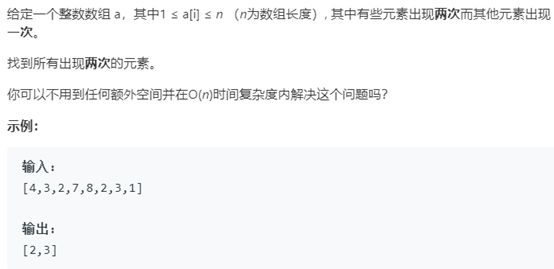
例6 数组中重复的数据
题号:442,难度:中等
题目描述:
解题思路:
可采用数组下标来判定出现两次的元素。题目中表明1 <= a[i] <= n,那么出现两次的元素i,对应下标i -1,出现一次时使得a[i - 1] * -1,当再次出现a[i - 1]小于零时,那么i就出现了两次。
具体代码:
class Solution {
public:
vector findDuplicates1(vector& nums) { // 方法1
vector result;
for(int i = 0;i < nums.size();i++) {
int j = abs(nums[i]) - 1;
if(nums[j] < 0)
result.push_back(j + 1);
else
nums[j] *= -1;
}
return result;
}
vector findDuplicates(vector& nums) { // 方法2 先排序再取重
vector vec;
sort(nums.begin(), nums.end());
for (int i = 1; i < nums.size(); i++) {
if (nums[i] == nums[i - 1]) {
vec.push_back(nums[i]);
}
}
return vec;
}
};
执行结果:
例7 数组拆分I
题号:561,难度:简单
题目描述:
解题思路:
题目中有说明元素的范围,且比较小。观察示例的数据发现,只需要对数据进行从小到大排序,依次选取两个元素中第一个元素作为最终结果的一部分即可。此时,可以采取数据哈希的思路来完成数据的排序操作,时间复杂度为O(n)。
具体代码:
class Solution {
public:
int arrayPairSum(vector& nums) {
sort(nums.begin(), nums.end());
int sum = 0;
for (int i = 0; i < nums.size(); i += 2) {
sum += nums[i];
}
return sum;
}
};
执行结果:
例8 优美的排列II
题号:667,难度:中等
题目描述:
解题思路:
此题考察我们寻找数学规律。先从1到k存储每个元素,然后从k+1开始每两个数存储(n--, k++)即可。
具体代码:
class Solution {
public:
vector constructArray(int n, int k) {
vector result(n);
int temp = 1;
for(int i = 0;i < n - k;i++)
result[i] = temp++;
int count = n;
bool judge = true;
for(int i = n - k;i < n;i++) {
if(judge) {
result[i] = count--;
judge = false;
} else {
result[i] = temp++;
judge = true;
}
}
return result;
}
};
执行结果:
例9 最多能完成排序的块 II
题号:768,难度:困难
题目描述:
解题思路:
此题考察双指针和动态规划思想的应用。双指针,从右边依次遍历存储当前的最小值。从左边开始依次遍历,存储当前的最大值。如果左边当前的最大值小于等于右边的最小值,则可以分割为一个块。
具体代码:
class Solution {
public:
int maxChunksToSorted(vector& arr) {
int n = arr.size();
vector rightMin(n);
for (int i = n - 1; i >= 0; i--) {
if (i == n - 1) {
rightMin[i] = arr[i];
} else {
rightMin[i] = min(arr[i], rightMin[i+1]);
}
}
int result = 1;
int leftMax = 0;
for (int i = 0; i < n - 1; i++) {
if(arr[leftMax] <= rightMin[i + 1]) {
result++;
leftMax = i + 1;
} else {
if(arr[leftMax] < arr[i]) leftMax = i;
}
}
return result;
}
};
执行结果:
例10 最佳观光组合
题号:1014,难度:中等
题目描述:
解题思路:
此题是一个双指针和动态规划思想的应用。可以把得分拆为两个部分,左边遍历,寻找max(A[i] + i);右边遍历,寻找max(A[j] - j)。可以采用一个数组保存右边最大值,让后从左边开始遍历,不断更新最终的最大值。
具体代码:
class Solution {
public:
int maxScoreSightseeingPair(vector& A) {
int n = A.size();
vector rightMax(n);
for(int i = n - 1; i >= 0; i--) {
if(i == n - 1)
rightMax[i] = A[i] - i;
else
rightMax[i] = max(A[i] - i, rightMax[i+1]);
}
int result = 0;
for(int i = 0;i < n - 1; i++)
result = max(result, A[i] + i + rightMax[i+1]);
return result;
}
};
执行结果:
例11 到最近的人的最大距离
题号:849,难度:简单
题目描述:
解题思路:
此题考察我们双指针的思想应用。可以采用一个指针从右边依次遍历,存储到当前元素的连续零的个数(此处需要注意尾部全为零的特殊情况)。然后,从左边开始遍历,计算左边连续零的个数,最后比较左边和右边零个数的大小即可。
具体代码:
class Solution {
public:
int maxDistToClosest(vector& seats) {
int n = seats.size();
vector right(n);
for (int i = n - 1; i >= 0; i--) {
if (i == n - 1) {
right[i] = seats[i] == 1 ? 0 : 1;
} else if (seats[i] == 0) {
right[i] = 1 + right[i+1];
}
}
int result = 0, left = n;
for (int i = 0; i < n; i++) {
if (seats[i] == 1) {
left = 1;
} else {
int temp = left;
if(right[i] < left && right[i] + i < n) {
temp = right[i];
}
result = max(result, temp);
left++;
}
}
return result;
}
}; 执行结果:
例12 分割数组
题号:915,难度:中等
题目描述:
解题思路:
此题同样是双指针思路的应用,但是可采用当前最大值和左数组最大值的思想来做。
具体代码:
class Solution {
public:
int partitionDisjoint1(vector& A) {
int n = A.size();
vector rightMin(n);
for(int i = n - 1;i >= 0;i--) {
if(i == n - 1)
rightMin[i] = A[i];
else
rightMin[i] = min(A[i], rightMin[i+1]);
}
int result = 0, rleftMax = A[0];
for (; result < n - 1;result++) {
rleftMax = max(A[result], rleftMax);
if(rleftMax <= rightMin[result + 1])
break;
}
return result + 1;
}
int partitionDisjoint(vector& A) { //当前最大值和左边最大值
if (A.size() == 0) {
return 0;
}
int leftMax = A[0];
int maxValue = A[0];
int index = 0;
for (int i = 0; i < A.size(); i++) {
maxValue = max(maxValue, A[i]);
if(A[i] < leftMax) {
leftMax = maxValue;
index = i;
}
}
return index + 1;
}
};
执行结果:
例13 将字符串翻转到单调递增
题号:926, 难度:中等
题目描述:
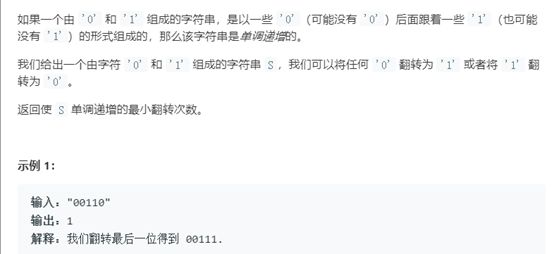
解题思路:
此题考察我们的数学思维。统计从左到右遍历时0的个数和1的个数,一旦零的个数大于1,结果自动增加1的个数,同时把0和1的个数置零,从新开始统计。
具体代码:
class Solution {
public:
/*
* 某一位为1时,前面一位是0或者1都可以
* 某一位为0时,前面一位只能为0
*/
int minFlipsMonoIncr(string S) {
int zero = 0, one = 0;
int result = 0;
for(char s: S){
if(s == '0')
zero++;
else
one++;
if(zero > one) {
result += one;
zero = 0;
one = 0;
}
}
result += zero;
return result;
}
};
执行结果:
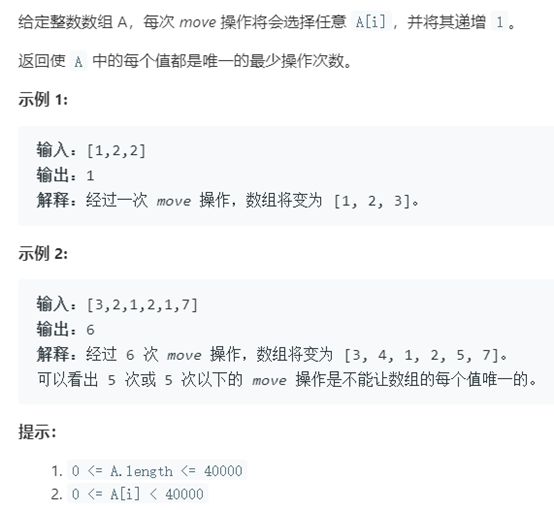
例14 使数组唯一的最小增量
题号:945,难度:中等
题目描述:
解题思路:
此题提示说明,0 <= A[i] < 40000。可知可以采用数组哈希的思想来求解本题,以空间换时间的思想,最终的时间复杂度为O(n)。
具体代码:
class Solution {
public:
int minIncrementForUnique1(vector& A) { // 超时
vector valueA;
sort(A.begin(), A.end());
for(auto a: A)
valueA[a]++;
int result = 0;
for(int i = 0;i < A.size();i++) {
if(valueA[A[i]] == 1)
continue;
int temp = A[i];
int count = 0;
while(valueA[temp] > 1) {
valueA[temp]--;
while(valueA[A[i]] > 0) {
count++;
A[i]++;
}
valueA[A[i]]++;
result += count;
}
}
return result;
}
int minIncrementForUnique(vector& A) {
sort(A.begin(), A.end());
int n = A.size();
int ans = 0;
for (int i = 1, j = 0; i < n; i++) {
if (A[i] - A[j] < i - j) { // 如果数字差小于数之间间隔,那么需要增加
ans += (A[j] + (i - j) - A[i]);
} else { // 否则建立新的比较起点
j = i;
i = j;
}
}
return ans;
}
};
执行结果:
本期讲思维转换类型问题,共7道题,三道简单题,四道中等题。
此部分题目是作者认为有价值去做的一些题,但是其考察的知识点不在前三篇总结系列里面。
- 例1解法:采用数组索引位置排序的思想。
- 例2解法:考察了组合数学的组合公式应用。有点类似动态规划的思想。
- 例3解法: 考察灵活运用二进制和整除余数的数学知识。
- 例4解法:动态规划思想的应用。
- 例5解法:分类讨论的数学思想。
- 例6解法:考察灵活运用哈希字典。
- 例7解法:考察闰年的数学判断公式,计算周几的细节处理能力。
例1 最大宽度坡
题号:962,难度:中等
题目描述:
解题思路:
采用索引排序的思路,使得从前往后遍历时,A[i] < A[j]。然后不断更新i的最小值,当前遍历的索引即为j。即可求取最终结果。
具体代码:
class Solution {
public:
int maxWidthRamp1(vector& A) { // 超时
int n = A.size();
int res=0;
for(int i = 0; i < n; i++){
for(int j = 0; j= A[j]) {
res = max(res, i-j);
break;
}
}
}
return res;
}
int maxWidthRamp(vector& A) { // 单调栈
stack s;
int res = 0, n = A.size();
for (int i = 0; i < n; i++) {
if (s.empty() || A[s.top()] > A[i]) s.push(i);
}
for (int i = n - 1; i >= res; i--) {
while (!s.empty() && A[s.top()] <= A[i]) {
res = max(res, i - s.top()), s.pop();
}
}
return res;
}
};
执行结果:
例2 总持续时间可被60整除的歌曲
题号:1010,难度:简单
题目描述:
解题思路:
本题考察了组合数学公式的应用,以及数学知识的转换和迁移应用。
具体代码:
class Solution {
public:
int numPairsDivisibleBy60(vector& time) {
vector temp(60);
int result = 0;
for(auto t: time) {
if(t % 60 == 0)
result += temp[0];
else
result += temp[60 - (t % 60)];
temp[t % 60]++;
}
return result;
}
}; 执行结果:
例3 可被5整除的二进制前缀
题号:1018,难度:简单
题目描述:
解题思路:
此题需要抓住整除的核心,即个位数是5的倍数时,即可整除5。我们只需要统计当前二进制数的个位数即可。
具体代码:
class Solution {
public:
vector prefixesDivBy5(vector& A) {
vector ans;
int num = 0;
for (int i = 0;i < A.size();i++) {
num <<= 1;
num += A[i];
num %= 10;
ans.push_back(num % 5 == 0);
}
return ans;
}
}; 执行结果:
例4 不相交的线
题号:1035,难度:中等
题目描述:
解题思路:
此题考察我们动态规划思想的应用。动态递推方程:可参考代码。
具体代码:
class Solution {
public:
int maxUncrossedLines(vector& A, vector& B) {
int n = A.size();
int m = B.size();
vector> dp(n+1, vector(m+1));
for (int i = 1; i < dp.size(); i++) {
for (int j = 1; j < dp[0].size(); j++) {
if (A[i - 1] == B[j - 1])
dp[i][j] = dp[i - 1][ j - 1] + 1;
else
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
}
}
return dp[n][m];
}
};
执行结果:
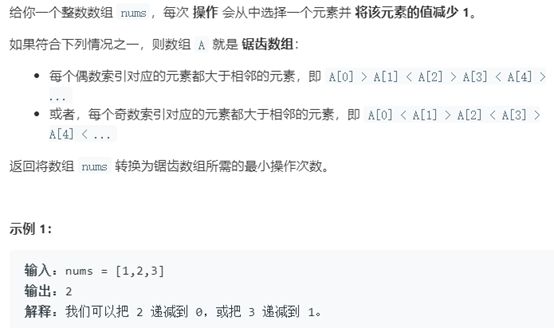
例5 递减元素使数组呈锯齿状
题号:1144,难度:中等
题目描述:
解题思路:
分类讨论。按照题目的意思,分奇数偶数讨论求解最终的最小操作次数即可。
具体代码:
class Solution {
public:
int movesToMakeZigzag(vector& nums) {
int odd = 0;
int eve = 0;
//偶数最高
for (int i = 0; i < nums.size(); i+=2) {
int temp = 0;
if(i ==0){
temp = nums [1];
}else if (i==nums.size() -1){
temp= nums[nums.size() -2];
}else {
temp = nums [i-1]>nums[i+1]?nums[i+1]:nums [i-1];
}
if(temp<=nums[i]){
eve+=nums[i]-temp+1;
}
}
//奇数最高
for (int i = 1; i < nums.size(); i+=2) {
int temp = 0;
if (i==nums.size() -1){
temp= nums[nums.size() -2];
}else {
temp = nums [i-1]>nums[i+1]?nums[i+1]:nums [i-1];
}
if(temp<=nums[i]){
odd+=nums[i]-temp+1;
}
}
return eve>odd?odd:eve;
}
};
执行结果:
例6 快照数组
题号:1146, 难度:中等
题目描述:
解题思路:
考察哈希字典的应用。
具体代码:
class SnapshotArray {
public:
int id;
unordered_map> data;
SnapshotArray(int length) {
id = 0;
}
void set(int index, int val) {
data[index][id] = val;
}
int snap() {
return id++;
}
int get(int index, int snap_id) {
auto it = data[index].upper_bound(snap_id);
if(it == data[index].begin())
return 0;
it--;
return it->second;
}
};
/**
* Your SnapshotArray object will be instantiated and called as such:
* SnapshotArray* obj = new SnapshotArray(length);
* obj->set(index,val);
* int param_2 = obj->snap();
* int param_3 = obj->get(index,snap_id);
*/
执行结果:
例7 一周中的第几天
题号:1185,难度:简单
题目描述:
解题思路:
此题考察闰年的数学判定公式,以及对于月份的边界处理,对于细节的处理考察比较多。也是一道锻炼我们代码能力的经典算法题。(PS:不能调用库函数)当然,此题还可以参考LeetCode的评论中,一个名为蔡乐公式的解法,但是一般是记不住的。
具体代码:
class Solution {
public:
string dayOfTheWeek1(int day, int month, int year) {
if(month==1||month==2) month+=12,year--;
int iWeek = (day + 2*month + 3*(month + 1)/5 + year + year/4 - year/100 + year/400)%7; //基姆拉尔森计算公式
string result[] = { "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday","Sunday"};
return result[iWeek];
}
// 普通方法 1971 01 01 friday
int month_days[13][2]={ {0, 0}, {31, 31}, {28, 29}, {31, 31}, {30, 30}, {31, 31}, {30, 30}, {31, 31}, {31, 31}, {30, 30}, {31, 31}, {30, 30}, {31, 31} };
string weeks[7]={"Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday"};
public:
//判断闰年
int isLeap(int year){
if((year%4==0 && year%100) || year%400==0) return 1;
else return 0;
}
int delta_days(int y1, int m1, int d1, int y2, int m2, int d2){
//默认 y1m1d1 > y2m2d2
int ans=0;
//时间调到m2月1日
while((y1>y2 || m1>m2 || d1>d2) && d2!=1){
ans++;
d2++;
if(d2==month_days[m2][isLeap(y2)]+1){
d2=1;
m2++;
}
if(m2==13){
m2=1;
y2++;
}
}
//按年跳
while(y1 > y2+1){
if(m2>2){
if(isLeap(y2+1)==1) ans+=366;
else ans+=365;
}
else{
if(isLeap(y2)==1) ans+=366;
else ans+=365;
}
y2++;
}
//按月跳
while(y1>y2 || m1>m2+1){
ans+=month_days[m2][isLeap(y2)];
m2++;
if(m2==13){
m2=1;
y2++;
}
}
//把时间准确调到y1m1d1
while(y1>y2 || m1>m2 || d1>d2){
ans++;
d2++;
if(d2==month_days[m2][isLeap(y2)]+1){
d2=1;
m2++;
}
if(m2==13){
m2=1;
y2++;
}
}
return ans;
}
string dayOfTheWeek(int day, int month, int year) {
int d; //d表示距2020.8.10(今天)的天数
if(year*10000+month*100+day > 20200810){
d = delta_days(year, month, day, 2020, 8, 10);
return weeks[(d+5)%7];//2020.8.27是周日
}
else{
d = delta_days(2020, 8, 10, year, month, day);
return weeks[(8-(d%7))%7];
}
}
};
执行结果: