力扣LeetCode(一)T01-T40
点击查看力扣LeetCode(二)T41-T80
文章目录
- 1.easy:两数之和(复杂度要为O(n))
- 2.easy:两数相加(链表怎么链起来?)
- 3.hard:无重复字符串的最长子串(滑动窗口&set去重)
- 4.寻找两个正序数组的中位数(要求时间O(log(m+n)))
- 5.最长回文子串
- 6. Z 字形变换
- 7.整数翻转(如何处理溢出的数据)
- 8.字符串转换整数 (atoi)(考虑越界截断)
- 9.回文数(判断一个数字是不是回文)
- 11.盛最多水的容器
- 12.整数转罗马数字
- 13.罗马数字转整数
- 14.最长公共前缀
- 15.三数之和
- 16.最接近的三数之和
- 17.电话号码的字母组合
- 18.四数之和
- 19. 删除链表的倒数第 N 个结点
- 20.有效的括号
- 21.合并两个有序链表(细节处理非常巧妙)
- 22.括号生成
- 24.两两交换链表中的节点
- 25.删除有序数组中的重复项
- 26.移除元素
- 28.实现 strStr()
- 29.两数相除
- 31.下一个排列
- 32.搜索旋转排序数组
- 34.在排序数组中查找元素的第一个和最后一个位置(三种二分模板)
- 35.搜索插入位置
- 36.有效的数独
- 38.外观数列
- 39.组合总和
- 40. 组合总和 II
1.easy:两数之和(复杂度要为O(n))
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。你可以按任意顺序返回答案。
1、用字典序map
注意初始化的时候之所以用i+1,是因为对于map中不存在的key,并且如果value值是int或者常量,默认值为0,
这里参见另一篇博客。https://blog.csdn.net/qq_44090228/article/details/120038984
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int,int> ump;
for(int i=0;i<nums.size();i++) {
ump[target-nums[i]]=i+1;//初始化:与map初始化值为0区分开
}
for(int i=0;i<nums.size();i++){
if(ump[nums[i]]>0&&ump[nums[i]]-1!=i){
return {ump[nums[i]]-1,i};
}
}
return {};
}
};
2、直接用find,就没有上文所说的胡扯八扯了。
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> hashtable;
for (int i = 0; i < nums.size(); ++i) {
auto it = hashtable.find(target - nums[i]);
if (it != hashtable.end()) {
return {it->second, i};
}
hashtable[nums[i]] = i;
}
return {};
}
};
3、下面是错误做法,用快排排序,再用双指针从头尾开始遍历,乍一看没问题,但是快排之后数组的值对应的索引
也改变了,这样求出来的值,自然就错了,所以这里排序是要记忆索引?使用pair,携带着数组中每个值对应的
原索引,这样的话复杂度就是O(nlogn+n),空间复杂度为O(n),直觉告诉我这不行。
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
vector<int> res;
if(nums.empty()) return res;
quicksort(nums,0,nums.size()-1);//快排排序
int p1=0,p2=nums.size()-1;//双指针
while(p1<p2&&nums[p2]+nums[p1]>target) p2--;
while(p1<p2&&nums[p2]+nums[p1]<target) p1++;
if(p1>=p2) return res;
res.push_back(p1);res.push_back(p2);
return res;
}
void quicksort(vector<int>&nums,int left,int right){
if(left>=right) return;
int i=left,j=right,base=nums[left];
while(i<j){
while(i<j&&nums[j]>=base) j--;
if(i<j) nums[i]=nums[j];
while(i<j&&nums[j]<base) i++;
if(i<j) nums[j]=nums[i];
}
nums[i]=base;
quicksort(nums,left,i-1);
quicksort(nums,i+1,right);
}
};
2.easy:两数相加(链表怎么链起来?)
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。

1、其实难点主要还是怎么将链表链起来。那么怎么把链表链起来呢?流程如下:
newhead=new();这是新链表的头结点
move=newhead;这是新链表的移动指针
while(){
tmp=new();构造下一个新的节点,如果直接move->next=new(),会运行出错的!
move->next=tmp;把新节点链接到链表中
move=move->next;移动指针移动,继续去构造并链接一个新的节点
}
2、另外要注意的就是最后如果有进位值还是要构造对应的新节点并链接起来。
3、空间o(1)(不是吧??明明构造了新节点使用了new()啊) 时间O(MAX(N+M))
—————————————————————————————————————————————————————————————————————————————————————————
代码可以写简短一些: 维护了一个变量t,那个更长的链表就不必单独再去遍历多出的节点了
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode dummyHead = new ListNode(-1), pre = dummyHead;
int t = 0;
while (l1 != null || l2 != null || t != 0) {
if (l1 != null) {
t += l1.val; l1 = l1.next;
}
if (l2 != null) {
t += l2.val; l2 = l2.next;
}
pre.next = new ListNode(t % 10);
pre = pre.next;
t /= 10;
}
return dummyHead.next;
}
}
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
if(l1==NULL) return l2;
if(l2==NULL) return l1;
ListNode* res,*move=NULL,*tmp,*p1=l1,*p2=l2;
res=new ListNode((p1->val+p2->val)%10);
move=res;
int up=(p1->val+p2->val)/10;
p1=p1->next;p2=p2->next;
while(p1!=NULL&&p2!=NULL){
tmp=new ListNode((p1->val+p2->val+up)%10);
move->next=tmp;
up=(p1->val+p2->val+up)/10;//进位值
move=move->next;
p1=p1->next;p2=p2->next;
}
while(p1!=NULL){
tmp=new ListNode((p1->val+up)%10);
move->next=tmp;
up=(p1->val+up)/10;//进位值
move=move->next;
p1=p1->next;
}
while(p2!=NULL){
tmp=new ListNode((p2->val+up)%10);
move->next=tmp;
up=(p2->val+up)/10;//进位值
move=move->next;
p2=p2->next;
}
if(up) {//最后这个进位可不要忘记!
tmp=new ListNode(up);
move->next=tmp;
}
return res;
}
};
3.hard:无重复字符串的最长子串(滑动窗口&set去重)
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int maxStr=0,left=0;//left是左边界
unordered_set<char> se;
for(int i=0;i<s.size();i++){//枚举右边界
while(se.find(s[i])!=se.end()){//这里要是不放心可以添加一个left
se.erase(s[left]);//删除窗口内的值
left++;//左边界同步进行右移动
}
se.insert(s[i]);//把重复的该删的也给删掉了,是时候将这个值加入滑动窗口了
maxStr=max(maxStr,i-left+1);
}
return maxStr;
}
};
写法2:需要注意的是,还在窗口内的字符要保持标记,离开窗口的一定要清除标记
class Solution {
public:
int lengthOfLongestSubstring(string s) {
unordered_map<char,int> vis;
int l=0,r=0,max_len=0;
while(r<s.size()){
if(vis[s[r]]==0) vis[s[r]]=1;//s[r]不重复,进入窗口内,并进行标记
else{//s[r]存在重复值,移动左指针,缩小窗口
while(s[l]!=s[r]) {
vis[s[l]]=0;//离开窗口的字符标记清除
l++;
}
l++;
}
max_len=max((r-l+1),max_len);
r++;
}
return max_len;
}
};
4.寻找两个正序数组的中位数(要求时间O(log(m+n)))
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

5.最长回文子串
1、动态规划:O(N^2) s[i:j]是回文子串的条件是s[i+1:j-1]&&s[i]=s[j]
class Solution {
public:
string longestPalindrome(string s) {
int sz=s.size(),left=0,right=0,maxlen=1,begin=0;
vector<vector<int> > dp(sz,vector<int>(sz,0));//初始化为0
for(int i=0;i<sz;i++) dp[i][i]=1;//单个字符一定是回文的
for(int len=2;len<=sz;len++){//必须枚举长度,这样的话,计算flag[i][j]时候才能保证flag[i+1][j-1]在之前已经算出来了
for(left=0;left<sz;left++){
right=left+len-1;
if(right>=sz) break;
if(s[left]==s[right]){
if(len<=3) dp[left][right]=1;
else dp[left][right]=dp[left+1][right-1];
}
if(dp[left][right]&&len>maxlen){
maxlen=len;
begin=left;
//break;//本意是以为不需要把所有长度为len的都找出来所以用break,后面发现不行,因为你要对dp进行初始化啊
//比如len=2的情况,我们找准了[0,1]符合条件,那如果及时终止了,dp[1,2],dp[2,3]....本该是1的,但是break后,就没有进行赋值为1
}
}
}
return s.substr(begin,maxlen);//记录下begin和maxlen,只在最后return的时候使用substr,而不是在循环里就使用substr,那样会很慢的!!!
}
};
2、暴力枚举:会超时
class Solution {
public:
string longestPalindrome(string s) {
string res="";
int flag=0;
for(int len=1;len<=s.size();len++){ //枚举每个回文子串可能的长度
for(int start=0;start<s.size();start++){ //枚举每个回文子串可能的其实位置
flag=0;
for(int i=start,j=start+len-1;i<=j&&j<s.size();i++,j--){
if(s[i]!=s[j]) {
flag=0;break;
}
flag=1;
}
if(flag&&len>res.size()) res=s.substr(start,len);
}
}
return res;
}
};
6. Z 字形变换
将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 “PAYPALISHIRING” 行数为 3 时,排列如下:

之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,比如:“PAHNAPLSIIGYIR”。
聪明做法:取模思维。时间: O ( n ) O(n) O(n),空间: O ( n ) O(n) O(n) 找准规律,找准周期 c y c l e = 2 ∗ n u m R o w s − 2 cycle=2*numRows-2 cycle=2∗numRows−2之后遍历字符串s并对其索引进行取模。取模后的操作如下图,把本该是同一行的内容存储到一个字符串中

class Solution {
public:
string convert(string s, int numRows) {
int sz=s.size(),cycle=numRows+numRows-2;
if(numRows<2) return s;
vector<string> v(numRows);
for(int i=0;i<sz;i++){
int mod=i%cycle;
if(mod<numRows) v[mod].push_back(s[i]);//行数递增存储
else v[cycle-mod].push_back(s[i]);//行数递减存储
}
string res="";
for(auto str:v) res+=str;
return res;
}
};
我自己的做法:不用被z字型吓到,其实根本用不着真的用这个z字型存储,比如针对于字符串“ILOVEENGLISHHOWABOUTYOU(我爱英语你呢)”,完全按行存储,获取结果的时候按列读取,当然你也可以存储的时候按列,读取的时候按行。

上图是按照行存储的,$符号表示这个地方不存储字符串s中的字符
class Solution {
public:
string convert(string s, int numRows) {
int sz=s.size(),groupsz=numRows+numRows-2;
if(numRows<2) return s;//注意这里的特殊情况
int group=sz/groupsz+(sz%groupsz>0?1:0);
int cols=numRows,rows=2*group; //确定出二维数组应该申请多大的内存
vector<vector<char> > tmp(rows,vector<char>(cols,'$'));
int tmprows=0,tmpcols=0,idx=0;
for(tmprows=0;tmprows<rows;tmprows=tmprows+2){//处理长度为numRows的列,从左到右存
for(tmpcols=0;tmpcols<cols&&idx<sz;tmpcols++) tmp[tmprows][tmpcols]=s[idx++];
idx=idx+cols-2;
}
idx=cols;
for(tmprows=1;tmprows<rows;tmprows=tmprows+2){//处理长度为numRows的列,从右到左存
for(tmpcols=cols-2;tmpcols>0&&idx<sz;tmpcols--) tmp[tmprows][tmpcols]=s[idx++];
idx=idx+cols;
}
string res;
for(int i=0;i<cols;i++){//答案要按列获取
for(int j=0;j<rows;j++){
if(tmp[j][i]!='$') res.push_back(tmp[j][i]);
}
}
return res;
}
};
7.整数翻转(如何处理溢出的数据)
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
解析:题目要求不允许使用 6464 位整数,即运算过程中的数字必须在 3232 位有符号整数的范围内,因此我们不能直接按照上述式子计算,需要另寻他路。

class Solution {
public:
int reverse(int x) {
int tmp=abs(x),res=0;
while(tmp){
if(res<INT_MIN/10||res>INT_MAX/10) return 0;
res=res*10+tmp%10;
tmp=tmp/10;
}
if(x<0) res=0-res;
return res;
}
};
8.字符串转换整数 (atoi)(考虑越界截断)
请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。
函数 myAtoi(string s) 的算法如下:
- 读入字符串并丢弃无用的前导空格
- 检查下一个字符(假设还未到字符末尾)为正还是负号,读取该字符(如果有)。 确定最终结果是负数还是正数。 如果两者都不存在,则假定结果为正。
- 读入下一个字符,直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
将前面步骤读入的这些数字转换为整数(即,“123” -> 123, “0032” -> 32)。如果没有读入数字,则整数为 0 。必要时更改符号(从步骤 2 开始)。 - 如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ,需要截断这个整数,使其保持在这个范围内。具体来说,小于 −231 的整数应该被固定为 −231 ,大于 231 − 1 的整数应该被固定为 231 − 1 。
- 返回整数作为最终结果。
注意:
- 本题中的空白字符只包括空格字符 ’ ’ 。
- 除前导空格或数字后的其余字符串外,请勿忽略 任何其他字符。
解析:这个题我是将 INT_MIN 和 INT_MAX 转化为字符串来和读入的字符串比较的,详细的思路在注释里。
class Solution {
public:
int myAtoi(string s) {
//1.记录上下限的数值部分(不管符号位):minStr=2147483648,maxStr=2147483647
int tmp=INT_MAX,idx=9,flag=1,res=0;//flag表示符号,res表示结果
string maxStr(10,' ');//2^31-1
while(tmp){
maxStr[idx--]=tmp%10+'0'; tmp=tmp/10;
}
string minStr(maxStr);
minStr[minStr.size()-1]+=1;//2^31
//2.读入有效数值部分并存储至num中
string num;
idx=0;
//去除前导空格
while(s[idx]==' ') idx++;
if(s[idx]=='+') flag=0,idx++;
else if(s[idx]>='0'&&s[idx]<='9') flag=0;
else if(s[idx]=='-') flag=1,idx++;
else return 0;//当前字符不是数字,读入暂停
//将num规范化
for(int i=idx;i<s.size()&&s[i]>='0'&&s[i]<='9';i++) num.push_back(s[i]);//中途遇到非数字就终止
for(idx=0;idx<num.size()&&num[idx]=='0';idx++)//去除前导0
num=num.substr(idx);//截取前导0之后的字符串 不管是正还是负,只保留了数字部分
if(num.empty()) return 0;
//3.转化为数字:如果是负数,那么如果数值部分长度大于minStr或者长度相等且值大于minStr,则越界;如果是正数,同理。
if(flag&&(num.size()>minStr.size()||num.size()==minStr.size()&&num>=minStr)) return INT_MIN;
if(!flag&&(num.size()>maxStr.size()||num.size()==maxStr.size()&&num>=maxStr)) return INT_MAX;
for(int i=0;i<num.size();i++) res=res*10+(num[i]-'0');
if(flag) return 0-res;
return res;
}
};
9.回文数(判断一个数字是不是回文)
给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。例如,121 是回文,而 123 不是。
解析,可以转化为字符串,然后左右两个指针,查看两个指针指向的值是否相等。注意处理特殊情况,比如数字值为0.
class Solution {
public:
bool isPalindrome(int x) {
string s;
if(x<0) s.push_back('-');
x=abs(x);
while(x){
s.push_back(x%10);
x=x/10;
}
int left=0,right=s.size()-1;
while(left<right&&s[left]==s[right]){
left++;right--;
}
if(left>=right) return 1;//这里的大于是为了处理x=0的情况
return 0;
}
};
11.盛最多水的容器
给你 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
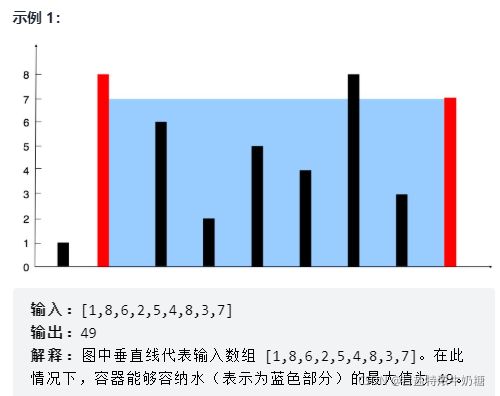
解析:双指针,至于左右两个指针,要移动哪个指针呢? 哪个指针对应的height小,就移动哪一个。
class Solution {
public:
int maxArea(vector<int>& height) {
int left=0,right=height.size()-1;
int cap=0;
while(left<right){
cap=max(cap,(right-left)*min(height[left],height[right]));
if(height[left]<height[right]) left++;
else right--;
}
return cap;
}
};
12.整数转罗马数字
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
- I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。
- X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。
- C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。
给你一个整数,将其转为罗马数字。
解析:对于罗马数字从左到右的每一位,选择尽可能大的符号值。对于 140140,最大可以选择的符号值为 C = 100 C = 100 \texttt{C}=100C=100 C=100C=100。接下来,对于剩余的数字 4040,最大可以选择的符号值为 XL = 40 X L = 40 \texttt{XL}=40XL=40 XL=40XL=40。因此,140140 的对应的罗马数字为 C + XL = CXL C + X L = C X L \texttt{C}+\texttt{XL}=\texttt{CXL}C+XL=CXL C+XL=CXLC+XL=CXL。
细节部分的处理:由于罗马数字从左到右每一位尽可能大,所以可以逆序遍历map,但是本意是想要用rbegin(),rend(),但是会报错,所以最后通过使用相反数来初始化map,从而顺序遍历也能达到逆序遍历的结果。
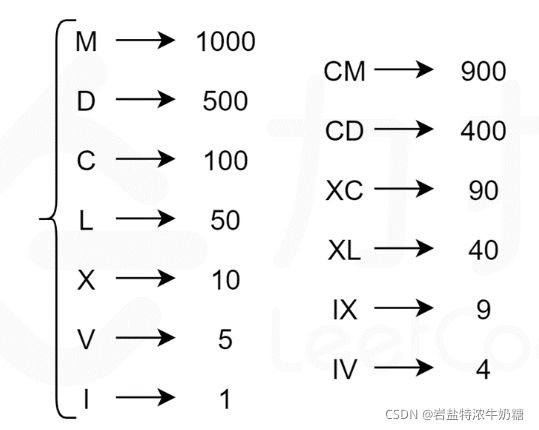
class Solution {
public:
string intToRoman(int num) {
map<int,string> mp{
{-1,"I"},{-5,"V"},{-10,"X"},{-50,"L"},{-100,"C"},{-500,"D"},{-1000,"M"},
{-4,"IV"},{-9,"IX"},{-40,"XL"},{-90,"XC"},{-400,"CD"},{-900,"CM"}
};
string res="";
for(auto it:mp){//逆序遍历
int tmp=0-it.first;
if(tmp<=num){
int cnt=num/tmp;
num=num%tmp;
while(cnt--) res+=it.second;
}
}
return res;
}
};
13.罗马数字转整数
class Solution {
public:
int romanToInt(string s) {
map<string,int> mp{
{"I",1},{"V",5},{"X",10},{"L",50},{"C",100},{"D",500},{"M",1000},
{"IV",4},{"IX",9},{"XL",40},{"XC",90},{"CD",400},{"CM",900}
};
int res=0;
for(int i=0;i<s.size();i++){
if(s[i]=='I'&&(s[i+1]=='V'||s[i+1]=='X')||s[i]=='X'&&(s[i+1]=='L'||s[i+1]=='C')||s[i]=='C'&&(s[i+1]=='D'||s[i+1]=='M')){
string tmp=""; tmp+=s[i]; tmp+=s[i+1];
i++;
res+=mp[tmp];
}
else{
string tmp="";
tmp+=s[i];
res+=mp[tmp];
}
}
return res;
}
};
14.最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 “”。
行式思维:
class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
string res="";
if(strs.empty()) return res;
res=strs[0];
for(int i=0,j=0;i<strs.size();i++){
for(j=0;j<res.size()&&j<strs[i].size();j++){ //
if(res[j]!=strs[i][j]) break;
}
res=strs[i].substr(0,j);
}
return res;
}
};
列式思维:
class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
string res="";
if(strs.empty()) return res;
int sz=strs[0].size();
for(int i=0;i<sz;i++){
for(int j=0;j<strs.size()-1;j++){
if(i<strs[j].size()&&strs[j][i]==strs[j+1][i]) continue;
else return res;
}
res.push_back(strs[0][i]);
}
return res;
}
};
15.三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
难点:如何去重!
这里的思路是,首先枚举我们选中的数字a,再用双指针的形式去寻找b和c。但是注意即使固定住a,b和c的值也可能不唯一,比如[-1,0,1], [-1,-1,2]
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int> > res;
sort(nums.begin(),nums.end());
for(int i=0;i<nums.size();i++){//选中这个数
if(nums[i]>0) return res;
if(i>0&&nums[i-1]==nums[i]) continue;//说明a已经取过这个值了
int tar=0-nums[i],left=i+1,right=nums.size()-1;
while(left<right){//以下循环中得出的b,c可能不唯一
while(left>i+1&&left<right&&nums[left]==nums[left-1]) left++;
//一开始忘了加left>i+1一直WA,这里如果不加left>i+1,也就是说left=i+1的时候,也会进行left++,
//形如排序后的数组如下:-4,-1,-1,0,1,2,当处理a=nums[1]=-1的情况时候,此时left=i+1,left再++,那么会导致b值取不到nums[2]=-1这个值,从而导致漏解。
//毕竟我们的目的是不让同一个值(a/b/c)取上同一个地方(同一个位置索引!)的值嘛
while(left<right&&nums[left]+nums[right]>tar) right--;
if(left<right&&nums[i]+nums[left]+nums[right]==0)
res.push_back({nums[i],nums[left],nums[right]});
left++;
}
}
return res;
}
};
16.最接近的三数之和
给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数,使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
class Solution {
public:
int threeSumClosest(vector<int>& nums, int target) {
sort(nums.begin(),nums.end());
int res=nums[0]+nums[1]+nums[2];
for(int i=0;i<nums.size();i++){
if(i>0&&nums[i-1]==nums[i]) continue;
int left=i+1,right=nums.size()-1;
while(left<right){
int tmp=nums[i]+nums[left]+nums[right];
if(tmp==target) return target;
if(abs(tmp-target)<abs(res-target)) res=tmp;
if(tmp>target){
right--;
while(left<right&&nums[right]==nums[right+1]) right--;//这里最开始还出错了
}
else{
left++;
while(left<right&&nums[left]==nums[left-1]) left++;//这里最开始还出错了
}
}
}
return res;
}
};
17.电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

示例:
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
BFS,比如输入234,其实就是把2对应的字符a,b,c入队,之后将a,b,c出队并在其后追加3对应的字符d,e,f,
之后ad,ae,af,bd,be,bf,cd,ce,cf再入队,之后再将这些出队,并追加3对应的字符并入队。最后队列里剩
下的值就是我们要求的结果。
class Solution {
public:
vector<string> letterCombinations(string digits) {
vector<string> v{"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
vector<string> res;
queue<string> q;
if(digits.empty()) return res;
int idx=digits[0]-'0';
int cnt=0,sz=v[idx].size();
for(int j=0;j<v[idx].size();j++) {
string tmp=""; tmp+=v[idx][j];
q.push(tmp);
}
for(int i=1;i<digits.size();i++){
while(cnt<sz){
string tmp=q.front();
q.pop();
cnt++;
for(int j=0;j<v[digits[i]-'0'].size();j++) q.push(tmp+v[digits[i]-'0'][j]);
}
sz=q.size();cnt=0;
}
while(!q.empty()) {
res.push_back(q.front());
q.pop();
}
return res;
}
};
18.四数之和
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] :
0 <= a, b, c, d < n
a、b、c 和 d 互不相同
nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按 任意顺序 返回答案 。
输入:nums = [1,0,-1,0,-2,2], target = 0
输出:[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int> > res;
sort(nums.begin(),nums.end());
int sz=nums.size();
//先选出两数之和,再选出两数之后,对这两个和进行双指针操作
for(int i=0;i<sz-3;i++){//选出第一个数
long long tmp=(long long)nums[i]+nums[sz-3]+nums[sz-2]+nums[sz-1];//转化为long long型
if(tmp<target) continue;//剪枝
tmp= (long long)nums[i]+nums[i+1]+nums[i+2]+nums[i+3];
if(tmp>target) break;//剪枝
if(i>0&&nums[i]==nums[i-1]) continue;//不要选上已经选过的数字
for(int j=i+1;j<sz-2;j++){//选出第二个数
if(j>i+1&&nums[j]==nums[j-1]) continue;
tmp=nums[i]+nums[j]+nums[sz-2]+nums[sz-1];
if(tmp<target) continue;//剪枝
tmp=nums[i]+nums[j]+nums[j+1]+nums[j+2];
if(tmp>target) break;//剪枝
int left=j+1,right=sz-1;
while(left<right){//之后双指针寻找后两个数
long long sum=(long long)nums[i]+nums[j]+nums[left]+nums[right];
if(sum==target) res.push_back({nums[i],nums[j],nums[left],nums[right]});
if(left<right&&sum>target) {
right--;
while(left<right&&nums[right]==nums[right+1]) right--;
}
else{
left++;
while(left<right&&nums[left]==nums[left-1]) left++;
}
}
}
}
return res;
}
};
19. 删除链表的倒数第 N 个结点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
进阶:你能尝试使用一趟扫描实现吗?

快慢指针,只遍历一次
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode*pfast=head,*pslow=head,*par=NULL;
for(int i=0;i<n-1;i++) pfast=pfast->next;
while(pfast->next!=NULL){
pfast=pfast->next;
par=pslow;
pslow=pslow->next;
}
if(par!=NULL) par->next=pslow->next;
else head=pslow->next;
delete pslow;
return head;
}
};
20.有效的括号
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
输入:s = "()[]{}"
输出:true
输入:s = "([)]"
输出:false
class Solution {
public:
bool isValid(string s) {
stack<char> st;
for(int i=0;i<s.size();i++){
if(s[i]=='('||s[i]=='['||s[i]=='{') st.push(s[i]);
if(s[i]==')'){
if(st.empty()||st.top()!='(') return 0;
st.pop();
}
if(s[i]==']'){
if(st.empty()||st.top()!='[') return 0;
st.pop();
}
if(s[i]=='}'){
if(st.empty()||st.top()!='{') return 0;
st.pop();
}
}
if(!st.empty()) return 0;
return 1;
}
};
21.合并两个有序链表(细节处理非常巧妙)
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
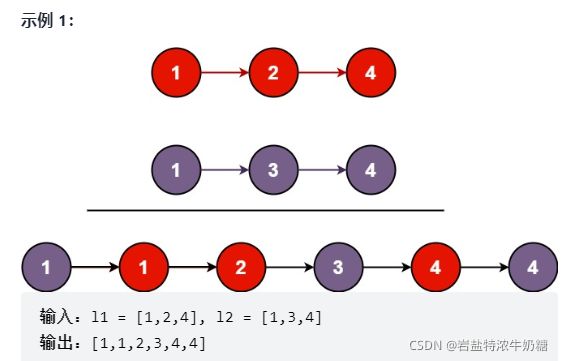
以前做过这种题目,但是以前每次处理,新建了节点,新链接起来的链表中的每个节点都是新创建的,空间复杂度飙升!
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
if(l1==NULL) return l2;
if(l2==NULL) return l1;
ListNode*head=new ListNode(-1);
ListNode* prev=head;
while(l1!=NULL&&l2!=NULL){
if(l1->val<l2->val){
prev->next=l1;
l1=l1->next;
}
else{
prev->next=l2;
l2=l2->next;
}
prev=prev->next;
}
prev->next=(l1==NULL?l2:l1);
return head->next;
}
};
22.括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
有效括号组合需满足:左括号必须以正确的顺序闭合
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
class Solution {
public:
vector<string> res;
vector<string> generateParenthesis(int n) {
if(n<=0) return res;
dfs("",n,0,0);
return res;
}
void dfs(string str,int n,int left,int right){
if(left>n||right>left) return;
if(str.size()==n*2){
res.push_back(str); return;
}
dfs(str+'(',n,left+1,right);
dfs(str+')',n,left,right+1);
}
};
24.两两交换链表中的节点
给定一个链表,两两交换其中相邻的节点,并返回交换后的链表。
你不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
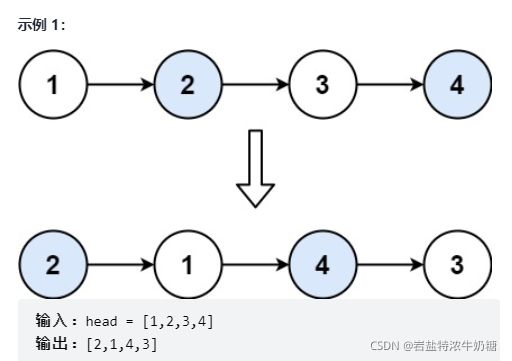
解析:做这道题的时候还是出现以前那样的情况:就是链表没链接起来,这真是个令人抓狂的问题。这里之前之所以没有链起来,是因为没有用前驱节点,只有一个par和cur,par是指向head的,那么再执行了par->next=cur->next; cur->next=par,再把par cur移动到下两个要处理的节点,最后返回head; 这样就会出现问题,比如当par还在head,cur还在head->next时,进行交换后,就相当于把cur移动到了head前面,但是我们最后返回的是head,自然就会遗漏节点。
究其原因其实就是因为没有前驱节点进行链接。如下代码中,par是前驱节点,再交换节点后至关重要的一步就是par->next=cur2。
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* newHead=new ListNode(-1);
newHead->next=head;
ListNode*par=newHead;
while(par->next!=NULL&&par->next->next!=NULL){
ListNode*cur1=par->next,*cur2=par->next->next;
cur1->next=cur2->next;
cur2->next=cur1;
par->next=cur2;//前驱节点链接
par=cur1;//移动par
}
return newHead->next;
}
};
25.删除有序数组中的重复项
给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

使用快慢指针,快指针去寻找不重复的元素,慢指针用于定位不重复的元素应该放到哪里(不重复元素应该去到的索引)
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
int sz=nums.size();
if(sz<=1) return sz;
int p1=0,p2=1;//慢指针、快指针
while(p2<sz){
if(nums[p2]!=nums[p2-1]) nums[++p1]=nums[p2];//快指针发现了不重复的元素,于是放到它该放的地方。
p2++;
}
return p1+1;//p1是最后一个不重复元素的索引,那么+1就是不重复数组的size了
}
};
26.移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
解析:思路和上一题几乎一致!
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
if(nums.empty()) return 0;
int p1=0,p2=0;
while(p2<nums.size()){
if(nums[p2]!=val) nums[p1++]=nums[p2];
p2++;
}
return p1;
}
};
28.实现 strStr()
实现 strStr() 函数。
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串出现的第一个位置(下标从 0 开始)。如果不存在,则返回 -1 。
说明:
当 needle 是空字符串时,我们应当返回什么值呢?这是一个在面试中很好的问题。
对于本题而言,当 needle 是空字符串时我们应当返回 0 。这与 C 语言的 strstr() 以及 Java 的 indexOf() 定义相符。
class Solution {
public:
int strStr(string haystack, string needle) {
if(needle.empty()) return 0;
int idx=0,res=-1;;
for(int i=0;i<haystack.size();i++){
if(haystack[i]==needle[idx]){
res=i;
int flag=i;
idx++;i++;
while(idx<needle.size()&&needle[idx]==haystack[i]&&i<haystack.size()){
idx++;i++;
}
if(idx==needle.size()) return res;
else i=flag,res=-1,idx=0;
}
}
return res;
}
};
29.两数相除
给定两个整数,被除数 dividend 和除数 divisor。将两数相除,要求不使用乘法、除法和 mod 运算符。
返回被除数 dividend 除以除数 divisor 得到的商。
整数除法的结果应当截去(truncate)其小数部分,例如:truncate(8.345) = 8 以及 truncate(-2.7335) = -2
提示:
被除数和除数均为 32 位有符号整数。
除数不为 0。
假设我们的环境只能存储 32 位有符号整数,其数值范围是 [−2^31, 2^31 − 1]。本题中,如果除法结果溢出,则返回 2^31 − 1。
一开始,是对除数进行+1操作,但是会超时,如果被除数很大,而除数是1,那么超时是必然的。
所以这里是指数趋势相加的。两个while循环。
我这里是把正数转化为负数处理的,这样的话溢出情况就可以减少一些。(如果转化为正数处理,那么
INT_MIN转成正数后就溢出了)
class Solution {
public:
int divide(int dividend, int divisor) {
if(dividend==INT_MIN&&divisor==-1) return INT_MAX;
int dend=dividend,sor=divisor;
if(dend>0) dend=-dend;
if(sor>0) sor=-sor;
long res=0,k=1;
while(dend<=sor){//当经过指数趋势处理后的除数过大,那么又回到外循环,除数也从原除数sor开始
long k=1,tmpsor=(long)sor;
while(dend<=tmpsor){//这里就是指数趋势的相加
dend-=tmpsor;
res+=k;
k+=k;//指数趋势
tmpsor+=tmpsor;
}
}
if(dividend>0&&divisor>0||dividend<0&&divisor<0) return (int)res;
else return (int)(0-res);
}
};
31.下一个排列
实现获取 下一个排列 的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列(即,组合出下一个更大的整数)。
如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。
必须 原地 修改,只允许使用额外常数空间。
输入 [5,6,1,2,4,3]
输出 [5,6,1,3,2,4]
预期结果 [5,6,1,3,2,4]
这个题难点主要是在于理解这个下一个排列,理解的关键点就在于 “组合出下一个更大的整数” 这句话
算法分三步:
第一步:数组中从后往前找到第一个nums[i-1]<nums[i],那么[i,sz]就是降序的。
第二步:从nums[sz]到nums[i]找到第一个比nums[i-1]大的数nums[j],然后交换nums[i-1]和nums[j]
第三步:将[i,sz]区间调整为升序,可用双指针。
如果整个数组都是降序的,那么就直接使用双指针,将整个数组调整为升序的。
class Solution {
public:
void nextPermutation(vector<int>& nums) {
int left=0,right=nums.size()-1;//如果整个数组都是降序的,那么双指针调整区间就是整个数组
for(int i=nums.size()-1,j=nums.size()-1;i>0;i--){
if(nums[i-1]<nums[i]){//找到第一个nums[i-1]
for(j=nums.size()-1;j>=i&&nums[j]<=nums[i-1];j--);//从后往前,找到第一个nums[j]>nums[i-1]
swap(nums[i-1],nums[j]);//交换
left=i,right=nums.size()-1;//需要用双指针将逆序转化为顺序的区间
break;
}
}
while(left<right){
swap(nums[left],nums[right]);
left++;right--;
}
}
};
32.搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
class Solution {
public:
int search(vector<int>& nums, int target) {
if(nums.empty()) return -1;
int left=0,right=nums.size()-1;
while(left<=right){
int mid=(left+right)/2;
if(nums[mid]==target) return mid;
if(nums[0]<=nums[mid]){//前半部分
if(target<nums[mid]&&target>=nums[0]) right=mid-1;
else left=mid+1;
}
// else{
if(nums[mid]<=nums[nums.size()-1]){//后半部分
if(target>nums[mid]&&target<=nums[nums.size()-1]) left=mid+1;
else right=mid-1;
}
}
return -1;
}
};
34.在排序数组中查找元素的第一个和最后一个位置(三种二分模板)
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你可以设计并实现时间复杂度为 O(log n) 的算法解决此问题吗?
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
解析:肯定是二分啊,但是学习了这么久的二分,我今天在做这道题的时候,才真的长记性了,有了下面这个知识点总结,以后的二分细节问题就能减少出错了。
二分模板1 :当我们将区间 [ l , r ] [l, r] [l,r] 划分成 [ l , m i d ] [l, mid] [l,mid] 和 [ m i d + 1 , r ] [mid + 1, r] [mid+1,r] 时,其更新操作是 r = m i d r = mid r=mid 或者 l = m i d + 1 l = mid + 1 l=mid+1,计算 mid 时不需要加1,即 m i d = ( l + r ) / 2 mid = (l + r)/2 mid=(l+r)/2 。
int bsearch_1(int l, int r){
while (l < r){
int mid = (l + r)/2;
if (check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
二分模板2:当我们将区间 [ l , r ] [l, r] [l,r] 划分成 [ l , m i d − 1 ] [l, mid - 1] [l,mid−1] 和 [ m i d , r ] [mid, r] [mid,r] 时,其更新操作是 r = m i d − 1 r = mid - 1 r=mid−1 或者 l = m i d l = mid l=mid,此时为了防止死循环,计算 mid 时需要加1,即 m i d = ( l + r + 1 ) / 2 mid = ( l + r + 1 ) /2 mid=(l+r+1)/2。
int bsearch_2(int l, int r){
while (l < r){
int mid = ( l + r + 1 ) /2;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
二分模板3:当我们将区间 [ l , r ] [l, r] [l,r] 划分成 [ l , m i d − 1 ] [l, mid - 1] [l,mid−1] 和 [ m i d + 1 , r ] [mid+1, r] [mid+1,r] 时,其更新操作是 r = m i d − 1 r = mid - 1 r=mid−1 或者 l = m i d + 1 l = mid+1 l=mid+1,此时 m i d = l + ( r − l ) / 2 mid = l+(r-l) /2 mid=l+(r−l)/2。
while(left<=right){//取等的
int mid=left+ (right-left) / 2;
if(check(mid)) res=mid,left=mid+1;
else right=mid-1;
}
return res;
———————————————————————————————————————————————————————
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
if(nums.empty()) return {-1,-1};
int left=0,right=nums.size()-1;
vector<int> res;
while(left<right){//左边第一个target
int mid=(left+right)/2;//这里本来加了1,但是出现死循环了,这里涉及一个二分模板的知识
if(nums[mid]>=target) right=mid;
else left=mid+1;
}
if(nums[right]!=target) return {-1,-1};
else res.push_back(right);
right=nums.size()-1;
while(left<right){//右边最后一个target
int mid=(left+right+1)/2;//这里必须+1,不然就会死循环
if(nums[mid]<=target) left=mid;
else right=mid-1;
}
res.push_back(right);
return res;
}
};
35.搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
输入: nums = [1,3,5,6], target = 5
输出: 2
输入: nums = [1,3,5,6], target = 2
输出: 1
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
if(nums.empty()||nums[0]>target) return 0;//特殊情况特殊处理
int left=0,right=nums.size()-1;
while(left<right){//如果没有target,那么left就是指向小于target的最大的一个数
int mid=(left+right+1)/2;
if(nums[mid]==target) return mid;
if(nums[mid]>target) right=mid-1;
if(nums[mid]<target) left=mid;
}
if(nums[left]==target) return left;
else return left+1;
}
};
36.有效的数独
请你判断一个 9x9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 ‘.’ 表示。
注意:
一个有效的数独(部分已被填充)不一定是可解的。
只需要根据以上规则,验证已经填入的数字是否有效即可。
输入:board =
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出:true
用空间换时间的算法,只需要扫描一遍board即可。
建立二维数组row,col,分别记录每行每列的数字出现的次数,一维索引标记行/列,二维索引标记数字。
建立三维数组box,表示盒子的位置,我们把盒子看做是一个整体,那么就相当于9x9的棋盘转化为3x3,那么每个盒子的行列索引就相当于
是盒子内小格子的行列索引的三分之一。
class Solution {
public:
bool isValidSudoku(vector<vector<char>>& board) {
int row[10][10]={0};
int col[10][10]={0};
int box[10][10][10]={0};
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
if(board[i][j]=='.') continue;
int num=board[i][j]-'0';
row[i][num]++;
col[j][num]++;
box[i/3][j/3][num]++;
if(row[i][num]>1||col[j][num]>1||box[i/3][j/3][num]>1) return 0;
}
}
return 1;
}
};
38.外观数列
给定一个正整数 n ,输出外观数列的第 n 项。
「外观数列」是一个整数序列,从数字 1 开始,序列中的每一项都是对前一项的描述。
你可以将其视作是由递归公式定义的数字字符串序列:
countAndSay(1) = “1”
countAndSay(n) 是对 countAndSay(n-1) 的描述,然后转换成另一个数字字符串。
前五项如下:
1. 1
2. 11
3. 21
4. 1211
5. 111221
第一项是数字 1
描述前一项,这个数是 1 即 “ 一 个 1 ”,记作 "11"
描述前一项,这个数是 11 即 “ 二 个 1 ” ,记作 "21"
描述前一项,这个数是 21 即 “ 一 个 2 + 一 个 1 ” ,记作 "1211"
描述前一项,这个数是 1211 即 “ 一 个 1 + 一 个 2 + 二 个 1 ” ,记作 "111221"
其实也是可以递归,但是这里我使用的迭代,但本质不变
class Solution {
public:
string countAndSay(int n) {
if(n==1) return "1";
string thelast="1";
for(int i=2;i<=n;i++){
string tmp="";
int cnt=0;
for(int j=0;j<thelast.size()-1;j++){//处理上一个字符串
cnt++;
if(thelast[j]!=thelast[j+1]){
char __cnt=cnt+'0';
tmp.push_back(__cnt);
tmp.push_back(thelast[j]);
cnt=0;
}
}
char __cnt=(++cnt)+'0';
tmp.push_back(__cnt);
tmp.push_back(thelast[thelast.size()-1]);
thelast=tmp;
}
return thelast;
}
};
39.组合总和
给定一个无重复元素的正整数数组 candidates 和一个正整数 target ,找出 candidates 中所有可以使数字和为目标数 target 的唯一组合。
candidates 中的数字可以无限制重复被选取。如果至少一个所选数字数量不同,则两种组合是唯一的。
对于给定的输入,保证和为 target 的唯一组合数少于 150 个。
还记得求组合的算法,吗?如下:
if(num==0){
for(int i=0;i
return;
}
if(id>=str.size()) return;//递归边界
res.push_back(str[id]); //把这个字符放到组合里面去
combination(str,id+1,num-1,res);
res.erase(res.end()-1);//不把这个字符放到组合里去
combination(str,id+1,num,res);
//我们先从头扫描字符串的第一个字符。针对第一个字符,我们有两种选择:
//第一是把这个字符放到组合中去,接下来我们需要在剩下的n-1个字符中选取m-1个字符;
//第二是不把这个字符放到组合中去,接下来我们需要在剩下的n-1个字符中选择m个字符。
这里其实异曲同工,但是需要注意的是,1)上面求组合是任意一个数字都能被选择或者不选择,这里的任意一个数字都能不选择,但是要符合target条件的才能被选择;2)每个数字可以重复选择,所以题解代码如下:
写法1:不太好理解,下次写我还是写不出来。。。。。 好好看写法2
class Solution {
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int> > res;
vector<int> tmp;
dfs(candidates,target,res,tmp,0);
return res;
}
void dfs(vector<int>&candidates,int target,vector<vector<int> >&res,vector<int>& tmp,int pos){
if(pos==candidates.size()) return;
if(target==0){
res.push_back(tmp); return;
}
dfs(candidates,target,res,tmp,pos+1);//每个数字都可以不被选择,直接跳过到下一个
if(target-candidates[pos]>=0){//但是并不是每个数字都能被选择,要符合这个条件的数字才能被选择
tmp.push_back(candidates[pos]);
dfs(candidates,target-candidates[pos],res,tmp,pos);//选择当前数,且重复选择了?
tmp.pop_back();//处理了这个数字被选择的情况,现在pop出来处理每个这个数字的情况。
}
}
};
写法2:更好理解
class Solution {
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
vector<vector<int> > res;
vector<int> tmp;
sort(candidates.begin(),candidates.end());
dfs(candidates,target,res,tmp,0);
return res;
}
void dfs(vector<int>&candidates,int target,vector<vector<int> >&res,vector<int>& tmp,int pos){
if(target==0){
res.push_back(tmp); return;
}
for(int i=pos;i<candidates.size()&&target-candidates[i]>=0;i++){
tmp.push_back(candidates[i]);
dfs(candidates,target-candidates[i],res,tmp,i);//是要重复! 所以是i
tmp.pop_back();
}
}
};
40. 组合总和 II
candidates 中的每个数字在每个组合中只能使用一次。
注意:解集不能包含重复的组合。
class Solution {
public:
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
vector<vector<int> > res;
vector<int> tmp;
sort(candidates.begin(),candidates.end());
dfs(candidates,target,0,res,tmp);
return res;
}
void dfs(vector<int>& candidates,int target,int pos,vector<vector<int> >&res,vector<int>&tmp){
if(target==0){
res.push_back(tmp); return;
}
for(int i=pos;i<candidates.size()&&target-candidates[i]>=0;i++){
if(i>pos&&candidates[i]==candidates[i-1]) continue; //避免重复选,1,1,1,1,6,7 target=3,这个例子中就能体现出这句代码可以去重的作用
tmp.push_back(candidates[i]);
dfs(candidates,target-candidates[i],i+1,res,tmp);//是i+1 !!! 不能重复的,上面那道题允许重复,所以是i
tmp.pop_back();
}
}
};
1,1,1,1,6,7 target=3,这个例子中就能体现出这句代码可以去重的作用
push了candistates[0]:1,之后for内进行dfs
push了candidates[1]:1,之后or内进行dfs
push了candidates[2]:1,发现满足target=3,之后return,返回原断点,也就是for内的dfs下一句,此时pos恢复1。
进行pop,现在tmp里面只有1,1。 之后继续for循环i++,此时i=3,pos=1, 正是因为有f(i>pos&&candidates[i]==candidates[i-1]) continue;
我们才不会把candidate[3]选上,如果选上的话,那么新的组合就是1,1,1,和组合candidates[0],[1],[2]重复了。