快速排序的三路划分方法和归并排序的递归和非递归实现
目录
快速排序的三路划分方法
归并排序的递归实现
归并排序的非递归实现
快速排序的三路划分方法
首先快排的时间复杂度为O(N*logN),空间复杂度O(logN),不稳定。
三路划分:将数据分为三份;可以提高当数据中出现多个重复数字时的效率。
如上图所示,小于key的值移动到左边,等于key的值放在中间,大于key的值移动到右边。
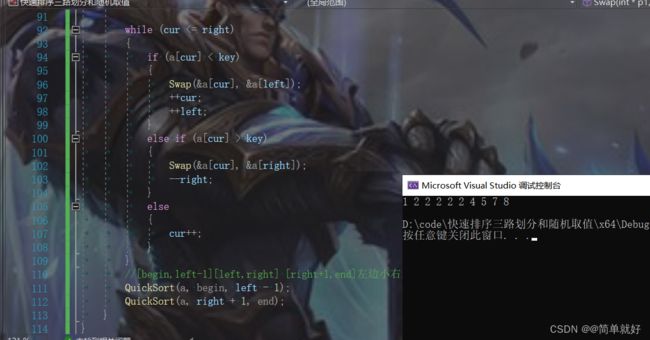
具体操作如下图所示:
核心思想:
- 比key小的值移动到左边
- 与key相等的值,往后移动
- 比key大的值移动到右边
- 与key相等的值移动到了中间
对于key的取值,我们选用随机取值的方法取值。因为如果使用三数取中的话,面对特殊用例的时候,可能大量区间选key让你选到比较小或者比较大的,导致性能下降。
代码:
#include /* printf, scanf, puts, NULL */
#include /* srand, rand */
#include /* time */
#include
void Swap(int *p1,int *p2)
{
int tmp=*p1;
*p1=*p2;
*p2=tmp;
}
void InsertSort(int* a, int n)
{
for (int i = 0; i < n-1; ++i)
{
int end = i;
int tmp = a[end + 1];
while (end>=0)
{
if (tmp a[end])
{
return begin;
}
else if (a[mid] < a[end])
{
return mid;
}
else
{
return end;
}
}
else//a[begin]>a[mid]
{
if (a[mid] > a[end])
{
return mid;
}
else if (a[begin] < a[end])
{
return begin;
}
else
{
return end;
}
}
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
if ((end - begin + 1) < 15)
{
//小区间用直接插入代替,减少递归调用次数
InsertSort(a + begin, end-begin+1);
}
else
{
int mid =GetMidIndex(a,begin,end);
Swap(&a[begin],&a[mid]);
int left=begin,right=end;
int key=a[begin];
int cur=begin+1;
while(cur<=right)
{
if(a[cur]key)
{
Swap(&a[cur],&a[right]);
--right;
}
else
{
cur++;
}
}
//[begin,left-1][left,right] [right+1,end]左边小右边大,中间的不处理
QuickSort(a, begin, left-1);
QuickSort(a, right+1, end);
}
}
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; ++i)
{
printf("%d ", a[i]);
}
printf("\n");
}
int main()
{
int a[]={2,1,2,7,2,2,4,5,2,8};
QuickSort(a,0,sizeof(a)\sizeof(int)-1);
PrintArray(a, sizeof(a) / sizeof(int));
return 0;
} 运行结果:
归并排序的递归实现
归并排序的时间复杂度为O(N*logN),空间复杂度O(N),稳定。
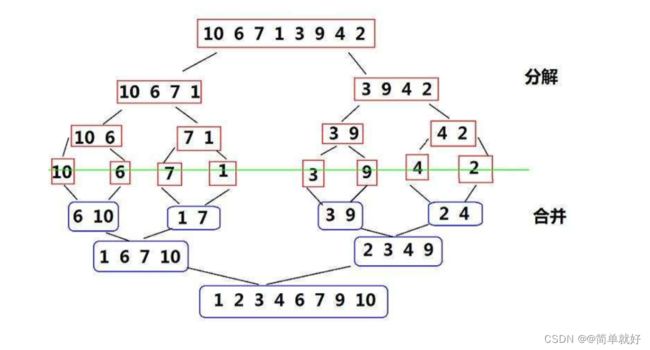
以升序为例,对于无序的数据,不断将数据划分为两个子区间,当每个子区间划分为只有一个数的时候认为有序,然后对每个子区间进行归并排序。
对于两个有序的子区间,依次比较,取小的尾插
当其中一个子区间尾插完,剩下的依次尾插到数组里;具体图下图所示。
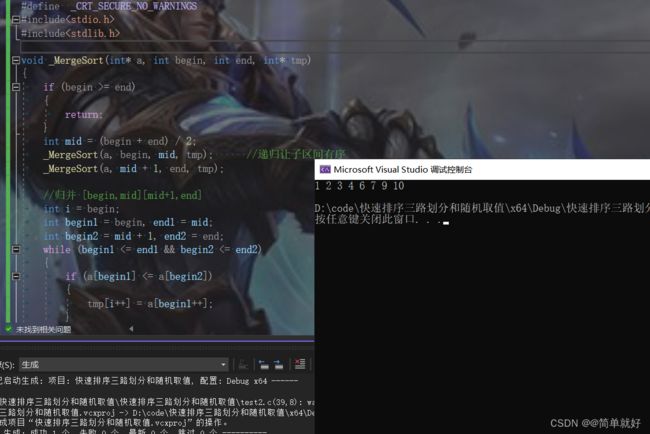
代码:
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin >= end)
{
return;
}
int mid = (begin + end) / 2;
_MergeSort(a, begin, mid, tmp); //递归让子区间有序
_MergeSort(a, mid + 1, end, tmp);
//归并 [begin,mid][mid+1,end]
int i = begin;
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
// 归并排序递归实现
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * (n));
if(tmp==NULL)
{
perror("malloc failed");
exit(-1);
}
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; ++i)
{
printf("%d ", a[i]);
}
printf("\n");
}
int main()
{
int a[]={10,6,7,1,3,9,4,2};
MergeSort(a,sizeof(a)\sizeof(int));
PrintArray(a, sizeof(a)\sizeof(int));
return 0;
}运行结果截图
归并排序的非递归实现
思想和递归的思想差不多,定义一个rangeN来控制数据跳动的步长,达到将数据分为子区间的效果。如下图所示。(begin1和end1作为左子区间的边界,begin2和end2作为右子区间的边界。)
但是控制不好会越界,越界访问需要注意的情况有
- end1 会越界
- begin2和end2越界
- end2越界
对于越界的边界,我们需要重新修正。
#define _CRT_SECURE_NO_WARNINGS
#include
#include
// 归并排序非递归实现
void MergeSortNonR(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
exit(-1);
}
int rangeN = 1;
while (rangeN < n)
{
for (int i = 0; i < n; i += 2 * rangeN)
{
int begin1 = i, end1 = i + rangeN - 1;
int begin2 = i + rangeN, end2 = i + 2 * rangeN - 1;
int j = i;
// end1 begin2 end2 越界
// 修正区间 ->拷贝数据 归并完了整体拷贝 or 归并每组拷贝
if (end1 >= n)
{
end1 = n - 1;
// 不存在区间
begin2 = n;
end2 = n - 1;
}
else if (begin2 >= n)
{
// 不存在区间
begin2 = n;
end2 = n - 1;
}
else if (end2 >= n)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
}
// 整体归并完了再拷贝
memcpy(a, tmp, sizeof(int) * (n));
rangeN *= 2;
}
free(tmp);
tmp = NULL;
}
void PrintArray(int* a, int n)
{
for (int i = 0; i < n; ++i)
{
printf("%d ", a[i]);
}
printf("\n");
}
int main()
{
int a[] = { 10,6,7,1,3,9,4,2 };
MergeSortNonR(a, sizeof(a)/sizeof(int));
PrintArray(a, sizeof(a)/sizeof(int));
return 0;
} 运行结果截图: