深入探讨磁盘B树的内部机制:代码实现与理论解析
深入探讨磁盘B树的内部机制:实际实现与理论解析
- 引言
- 一、背景知识:二叉树到B树的衍变
- 二、B树的性质
- 三、B树节点的定义
- 四、B树的添加
-
- 4.1、原理解析
- 4.2、代码实现
- 五、B树的删除
-
- 5.1、原理解析
- 5.2、代码实现
- 六、完整代码
- 总结
博主简介
一个热爱分享高性能服务器后台开发知识的博主,目标是通过理论与代码实践的结合,让世界上看似难以掌握的技术变得易于理解与掌握。技能涵盖了多个领域,包括C/C++、Linux、数据结构与算法、Nginx、MySQL、Redis、fastdfs、kafka、Docker、TCP/IP、协程、DPDK等。
️ CSDN实力新星、CSDN博客专家、华为云云享专家、阿里云专家博主
引言
红黑树、B/B+树、Hash是非常常用的数据结构,特别是布隆过滤器。这三个数据结构都是具备查找功能的,是一种强查找的数据结构。比如将它们用于存储一个集合,可以快速查找到指定的数据。排序的数据结构,在平常用的时候,基本上都是这几个。这篇文章都将帮助深入了解磁盘B树。
这篇文章将带领读者深入探讨磁盘B树的内部工作原理,提供了一种实际实现和理论解析相结合的方式。博主将手把手地教你理解B树的核心概念,包括节点结构、插入和删除操作,以及搜索算法。通过详细的示例和代码演示,学会如何构建和操作一个B树,从而提高数据存储的效率和性能。文章很长,耐心看完一定有所收获。

一、背景知识:二叉树到B树的衍变
在了解B树之前,先介绍一下二叉树。二叉树是一种常见的树状数据结构,它由节点组成,每个节点最多有两个子节点,分别称为左子节点和右子节点。二叉树具有以下特点:
-
树形结构:二叉树是一种层次结构,由根节点开始,每个节点可以有零、一个或两个子节点。这种结构使得数据可以以分层的方式进行组织和存储。
-
节点:二叉树的每个节点包含一个数据元素,通常表示某种值或对象,以及指向其左子节点和右子节点的指针(引用)。
-
根节点:树的顶部节点称为根节点。它是整个二叉树的起始点,所有其他节点都通过它连接。
-
叶节点:叶节点是没有子节点的节点,它们位于树的末端。
-
子树:每个节点的左子节点和右子节点都可以看作是一个独立的子树,这些子树也是二叉树。
再通俗一点,二叉树就是有两个叉的一种数据结构,二叉树的最大特点是最大的查询次数由树的层高决定。比如一个有1023个结点的二叉树,它的层高有10层;树的层高决定着查找时比较的次数,树的层数越多,对比的次数越多,寻址查找下一个节点的次数也变多。
二叉树的数据的存储在内存中的,准确的说是存储在一个进程的的堆上面的。二叉树的节点在内存上的排布:

内存上节点间可能连续,也可能不连续。树的形状是一个逻辑图,不是计算机系统中真实存在的树,物理内存上构建/组织出来的类似上图。因此,在查找时是通过不断对比寻找下一个节点,查找过程就是寻址过程;这里的寻址是说二叉树的节点中有一个指针指向内存,需要通过它来找到下一个内存块。
在内存中这种寻址效率是非常高的,这种查找到了的时间影响可以忽略不计。但是,可能有一些情况,数据会存储在磁盘中(内存不够时的虚拟内存、或者数据需要保存到磁盘中永久存储);这时候,如果数据在内存中没有命中,就需要到磁盘中查找;如果这些数据使用二叉树存储,并且节点存储在磁盘中,会发现每次查找下一个节点都要进行一次磁盘寻址,而磁盘寻址是一个非常耗时的操作,因此就衍生出一些降低层高的数据结构(平衡二叉树、AVL树、红黑树、B树和B+树)。
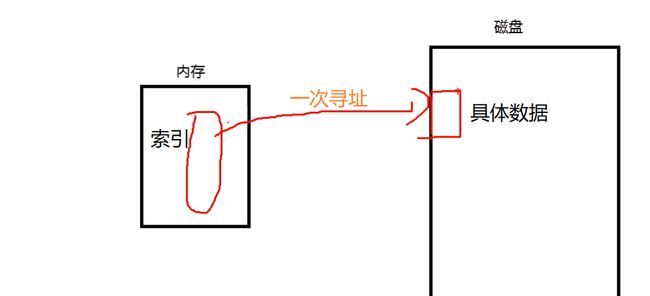
磁盘示意图如下:

在磁盘中,数据是存储在扇区上的,假设节点是4K,每次查找下一个节点相当于查找下一个扇区,这是一个极其耗时的操作。
对于二叉树,如果每一个节点都存储到磁盘中,那就相当于每次对比后找下一个节点都是一次磁盘寻址。层高越高,耗时越长。
所以,在磁盘中存储数据时二叉树不是一个很好的选择。因此衍生出了多叉树。多叉树(Multiway Tree)与二叉树不同,它允许一个节点可以有多个子节点,而不仅仅是两个。多叉树通常用于表示层次性数据,其中每个节点可以有零个或多个子节点,这些子节点之间没有固定的顺序。

通俗的讲,多叉树就是一个节点有多个叉。那么多叉树是如何降低层高的呢?二叉树如果有1024个节点,则层高是10;同样是1024个节点,4叉树每个节点存储3个数据,层高就为 l o g 4 ( 1024 ÷ 3 ) = 5 log_4(1024\div3) = 5 log4(1024÷3)=5。如果是更多叉的多叉树,那么层高会更低,比如1024叉,3层就可以存储1GB的数据。层数低带来的好处就是对比次数少,也就使得磁盘寻址次数少,从而加快查找速度。
注意,多叉树不等于B树,多叉树和B树的区别:
- 多叉树只是强调开叉,并没有强调所有节点在同一层上。比如,为了降低层高,多叉树只是开辟了多个叉允许一个节点可以有任意数量的子节点,而不限于特定的数量。每个节点的子节点数量可以是可变的,没有固定的规则。
- B树强调了所有的叶子节点在同一层。B树是一种平衡多路查找树,每个节点可以有多个子节点,但是在B树中,子节点的数量是有限的,通常被限制在一个范围内。B树通常是按照一定的度数(或阶数)来定义的,每个节点最多可以有该度数的子节点。
- 举个例子,5个节点的多叉树可能会连成一条线,它虽然开辟了多个叉,但是没有使用;而B树要求所有的叶子节点在同一层,也就是所有的叉都使用起来。
二、B树的性质
一颗M阶B树T,满足以下条件:
- 每个结点至多拥有M颗子树。
- 根结点至少拥有两颗子树。
- 除了根结点以外,其余每个分支结点至少拥有M/2课子树。
- 所有的叶结点都在同一层上。
- 有k课子树的分支结点则存在k-1个关键字,关键字按照递增顺序进行排序。
- 关键字数量满足ceil(M/2)-1 <= n <= M-1。
这些概念是一种学术概念,非常的严谨,所以会伴随一些数学公式 ,因为单纯的文字描述无法达到所需的严谨效果。从上面描述的性质中 ,可以提炼出一些关键词:“M”、“2”、“ M ÷ 2 M\div2 M÷2”、“同一层上”、“k与k-1”、“递增顺序”、“ceil(M/2)-1 <= n <= M-1”。
注意:关于第五条中的“关键字按照递增顺序进行排序”,这个是从数学严谨上角度所描述的,从工程应用的角度上说,“关键字按照递减顺序进行排序”也应该算是B树的范畴。
对上面的六个性质进行精简描述一下:
- 树开叉的数量上限是M颗,也就是定义了范围。
- 形容M颗子树与Key值的关系。
- 所有的叶子节点在同一层。
- 除了根节点以外,每个节点最少有 M ÷ 2 M\div2 M÷2颗子树。
三、B树节点的定义
为了代码实现方便,根据“除了根结点以外,其余每个分支结点至少拥有M/2课子树”的性质,会发现可以存在这样一组关系:M = 2 * SUB。因此,代码实现可以如下:
#define SUB_M 3
typedef struct _btree_node {
int keys[2*SUB_M - 1]; // key集合
// void * value;
struct _btree_node *childrens[2*SUB_M]; // 子树
int num; // 当前节点存储了多少个数据,即keys存储的数量
int leaf; // 代表是否为叶子节点
}btree_node;
上面的定义通过宏的方式将B树的叉数量固化了,为了灵活,也可以使用指针的方式,不定义具体的数量。
typedef struct _btree_node {
int *keys; // key集合
struct _btree_node **childres; // 子树
// void * value;
int num; // 当前节点存储了多少个数据,即keys存储的数量
int leaf; // 代表是否为叶子节点
}btree_node;
所以,当阅读代码,判断一个节点是不是B树时,可以借鉴上面的方式。
除了定义B树的普通节点,还要定义B树的根节点:
typedef struct _btree {
struct _btree_node *root;
int t; // M阶,t=M/2
}btree;
至此,B树的节点定义就算完成了。在这里再扩展一些知识:
- B-tree / B tree:这种名称定义都是说的B树,不存在B"减"树这个数据结构。
- B+tree:B树的所有节点都是存储数据的,B+树是B树的扩展或者变种,B+树的内节点不存储数据,只做索引,所有的数据都存储在叶子节点。此外,B+树适合范围查阅是由链表性质决定的。
- B+树更适合做磁盘索引,性能优于B树;因为B+树的内结点不存储数据。同样的内存空间,B树的结点除了要存储key值,还要存储value值,所以B树的节点会比B+树的节点内存占用大,从而存储B树的节点会少于B+树的节点。
- 内节点:有子节点的称为内节点
B树和B+树在使用场景上的差异说明:举个例子,假设有一个很大量的数据需要存储(比如100万个节点),内存上肯定无法全部存储,必然有很大部分在磁盘上。
- 如果使用B树进行存储,由于每个节点都存储数据,必然有一部分节点存储在内存中,一部分节点存储在磁盘上。
- 如果使用B+树存储,就有些不一样,由于B+树的内节点不存储具体数据,只做索引,所以B+树存储在内存中的节点数量会比B树多得多。所以,B+树做索引会更好,因为可以把所有的索引关系存储到内存中,然后通过一次性寻址找到存储具体数据的叶子节点。B树就无法做到这样,它只能一个节点一个节点的磁盘寻址。
- B树和B+树都可以做索引,但是B+树更常用于做索引,特别是索引磁盘数据。比如MySQL、mongodb、PostgreSql等数据库的索引使用的就是B+树。
四、B树的添加
4.1、原理解析
以六叉B树为例,演示添加26个英文字符的全过程,分析B树的添加原理。
首先是根节点的添加,在未满足分裂添加之前,添加过程如下:

接下来进入第一个难点:根节点分叉。
由原来的一个根节点分裂出三个节点:
- 将中间元素提取出来放在根节点;
- 然后比根节点小的放左边;
- 比根节点大的放右边。
如下图所示:
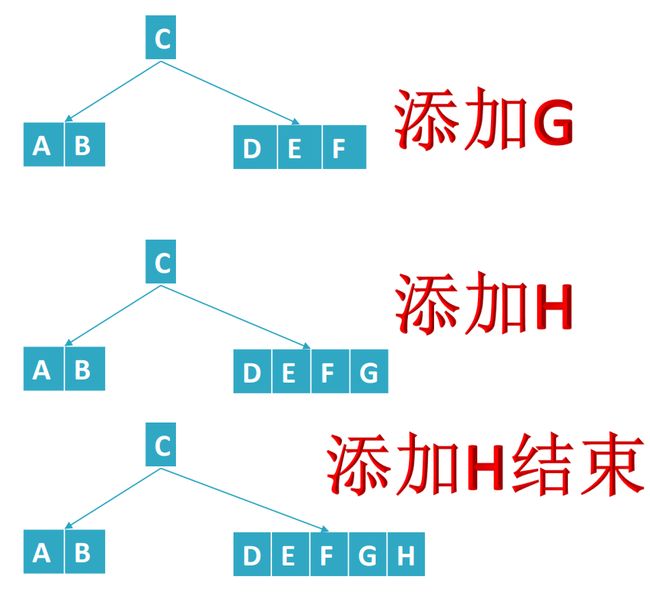
这时,再插入“I”,“I”比“C”大,放右边,但是右边的元素已经满5个,所以,进入第二个难点:节点分裂,将中间元素提取出来,放入父节点,原来的节点分裂成两个。如下图所示:

在这里可能会有疑问:为什么是中间的元素而不是两边的其中一个?
这是为了代码好实现而设计的,不是B树的定义决定,也可以取其他元素,但是不如取中间元素更优一些。取中间的元素作为分裂点,我们就可以定义key的数量为奇数,子树的数量为偶数;奇数可以让我们更好的将中间节点放入父节点中,然后分割出两个子树。
添加的时候,可以注意到:先分裂再添加。这很重要。
继续添加节点,直达到达下一个分裂条件:

继续添加,再次分裂,依旧是先分裂再添加的顺序:

继续添加,值得说明的是,在这颗六叉的B树中,当节点数量达到5时不会分裂,只有下一次插入时才会去分裂并添加。

继续添加:

这时候,发现根节点已经达到分裂的条件了。再添加节点就要开始对根节点进行拆分。

继续前面的步骤,继续添加节点,直到添加完26个字母。

可以思考一个问题:B树每次添加节点是添加到哪里?
B树添加节点都是添加到叶子节点,然后通过分裂将中间节点放到父节点,从而增加层高。 如果添加到中间节点,子树是比较难操作的,会添加代码的复杂性,效率不高而且不易维护。
B树在插入时采用插入叶子节点的方式是为了方便代码实现,通俗的说插入到叶子节点并且不违背B树性质是最容易实现的方式。
B树的查找时间复杂度是 l o g n ( m ÷ n ) log_n(m\div n) logn(m÷n) ,其中n是分叉数,m是节点数。
4.2、代码实现
B树的添加包含节点创建、分裂等操作;核心难点,根节点的分裂:1个分裂成3个。
(1)子节点、根节点的创建。
// 创建子节点
btree_node *btree_create_node(int t,int leaf)
{
btree_node *node = (btree_node *)calloc(1, sizeof(btree_node));
if (node == NULL)
return NULL;
node->keys = (KEY_VALUE *)calloc(1, (2 * t - 1)*sizeof(KEY_VALUE));
if (node->keys == NULL)
{
free(node);
return NULL;
}
node->childrens = (btree_node **)calloc(1, (2 * t)*sizeof(btree_node*));
if (node->childrens == NULL)
{
free(node->keys);
free(node);
return NULL;
}
node->leaf = leaf;
node->num = 0;
return node;
}
// 创建根结点
void btree_create(btree *T, int t) {
T->t = t;
btree_node *x = btree_create_node(t, 1);
T->root = x;
}
(2)子分裂节点:一分为二的情况。假设一颗M阶B数T,当B树的结点关键字达到M时,需要分裂。分裂时将M/2结点放到父结点,0 ~ (M/2-1)组成一个子树,(M/2+1) ~ (M-1)组成一个子树;当父结点结点关键字达到M时也要分裂。

代码实现如下:
// 子节点分裂
// 参数描述:T是B树、x是父节点、idx是指第几个子树。
void btree_split_child(btree *T, btree_node *x, int idx)
{
// 获取B树的阶数除2减1的值:M/2 - 1
int t = T->t;
// 保存x的对应索引的子树
btree_node *y = x->childrens[idx];
// 创建新节点
btree_node *z = btree_create_node(t,y->leaf);
// 设置新节点的可存放ke值数量
z->num = t - 1;
int i = 0;
// 将分裂节点的后面节点移动到新创建的节点中。
for (i = 0; i < t - 1; i++)
z->keys[i] = y->keys[t + i];
if (y->leaf == 0)//inner,内节点
{
for (i = 0; i < t; i++)
z->childrens[i] = y->childrens[t + i];
}
// 接下来操作y树
y->num = t-1;
// 对x的操作,移动、插入结点,保证B树有序性。
for (i = x->num; i >= idx + 1; i--)
{
x->childrens[i + 1] = x->childrens[i];
}
// 增加的子树保存到父节点
x->childrens[idx + 1] = z;
// 对x里的 key 进行交换,主要循环次数一定比childrens少一个。
for (i = x->num-1; i >= idx; i--)
{
x->keys[i + 1] = x->keys[i];
}
x->keys[idx] = y->keys[t-1];
x->num += 1;
}
(3)根节点分裂:一分为三的情况。先创建一个空节点(不存储任何数据),然后把空节点的第一颗子树(索引ID为0的子树)指向根节点;再将旧根节点的中间值放到空节点中;最后再分裂。

代码实现如下:
void btree_insert_nonfull(btree *T, btree_node *x, KEY_VALUE k) {
int i = x->num - 1;
if (x->leaf == 1) {
while (i >= 0 && x->keys[i] > k) {
x->keys[i + 1] = x->keys[i];
i--;
}
x->keys[i + 1] = k;
x->num += 1;
}
else {
while (i >= 0 && x->keys[i] > k) i--;
if (x->childrens[i + 1]->num == (2 * (T->t)) - 1) {
btree_split_child(T, x, i + 1);
if (k > x->keys[i + 1]) i++;
}
btree_insert_nonfull(T, x->childrens[i + 1], k);
}
}
void btree_insert(btree *T, KEY_VALUE key) {
btree_node *r = T->root;
if (r->num == 2 * T->t - 1) {
// 创建一个非叶子节点
btree_node *node = btree_create_node(T->t, 0);
// 更新根节点
T->root = node;
// 旧根节点赋给第一个子树
node->childrens[0] = r;
// 开始分裂
btree_split_child(T, node, 0);
// 开始插入
int i = 0;
if (node->keys[0] < key) i++;
btree_insert_nonfull(T, node->childrens[i], key);
}
else {
btree_insert_nonfull(T, r, key);
}
}
五、B树的删除
5.1、原理解析
假设存在这样一个B树:

现在想删除A这个节点,如果直接删除会违背B树的一个性质:“关键字数量满足ceil(M/2)-1 <= n <= M-1”。为了不违背这个性质,需要将节点合并,然后再删除。如下图所示:

这里合并C的原因是A比C小,所以合并C两侧的子树。这是第一种比较明显的情况:合并。
接下来看看删除B的过程:
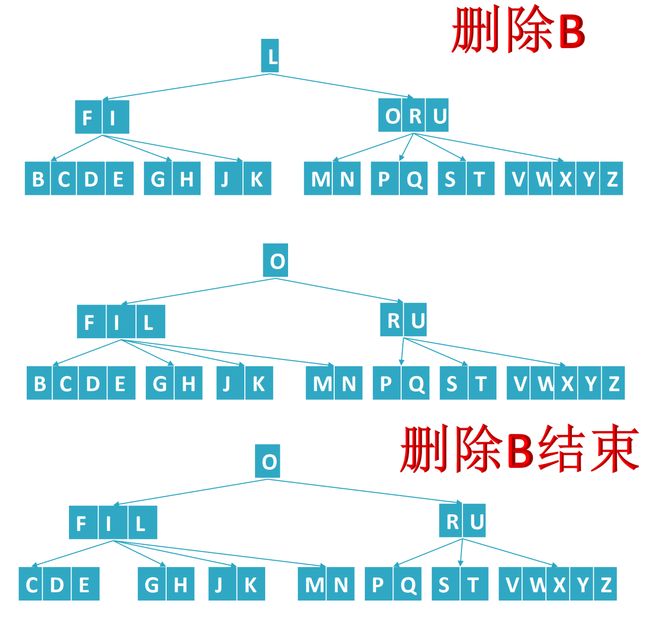
可以看到,这中间有一个借位的操作:把L放到左边,把O放在父节点;借位只能从父节点借位,不能从兄弟节点借位。因为从兄弟节点借位会打乱B树的有序性。
那么在什么时候需要借位呢?
当需要删除的节点的父节点的节点数量等于 ( M ÷ 2 ) − 1 (M\div 2) -1 (M÷2)−1时,则需要借位。借位的目的是为了避免资源不足。
再来看看删除C,删除C时直接删除不会影响B树的性质,因此可以直接删除。如下:
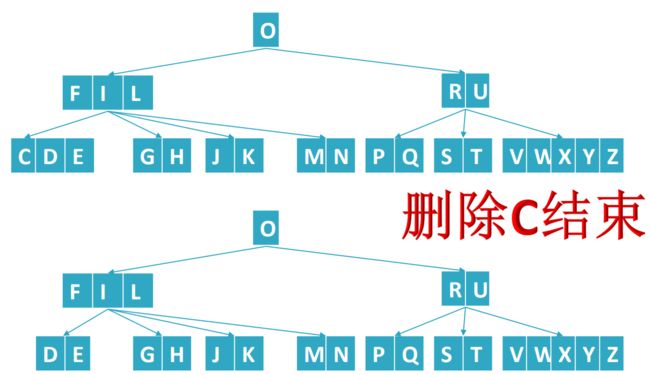
接着删除D,删除D和删除A的情况类似,需要合并。但是删除E就有点意思了,他需要借位,但是借不到了,怎么办呢?借不到就合并,如下:
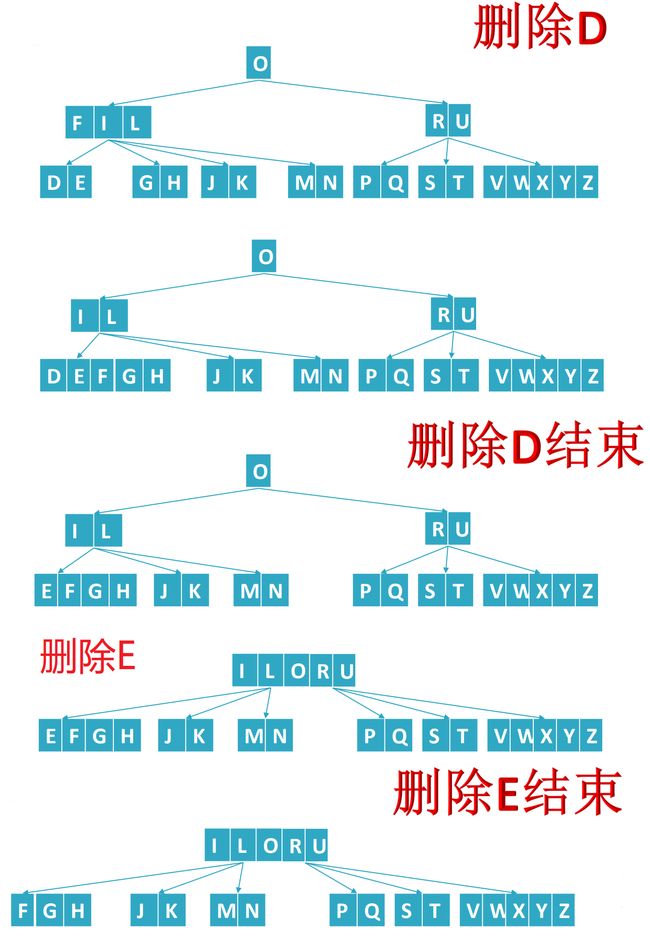
删除操作基本就上述几个情况,总结起来就是:先合并或借位,再删除;即先通过合并和借位的方式将B树转换为可删除的状态。
上面的演示,都是删除的叶子节点,那如果删除内节点呢?也是同样的,借位、合并、删除。如下删除O的过程:从叶子节点借位L放到当前位置,O合并到子节点,然后再删除。

5.2、代码实现
B树的删除包括:销毁、借位、合并等操作。借位是比较容易实现的,借位过程主要是赋值操作:在子树中找到满足key值数量大于 M ÷ 2 − 1 M\div 2 - 1 M÷2−1的条件,然后进行相关赋值。核心难点是合并操作。
(1)B树销毁节点。
void btree_destroy_node(btree_node *node)
{
if (node == NULL)
return;
if (node->childrens != NULL)
free(node->childrens);
if (node->keys != NULL)
free(node->keys);
free(node);
}
(2)合并。假设一颗M阶B数T,当要删除的结点所在子树的key数量等于ceil(M/2)时,需要进行合并。
/*************************合并 merge*****************************/
// 参数说明:T是B数,x是合并的父节点,idx是合并第几颗子树。
void btree_merge(btree *T, btree_node *x, int idx)
{
// 先保存要合并的两个子树
btree_node *left = x->childrens[idx];
btree_node *right = x->childrens[idx + 1];
// 先将要合并的key值保存到要合并的子树中
left->keys[T->t-1] = x->keys[idx];
// 合并keys
int i = 0;
for (i = 0; i < T->t-1; i++)
{
left->keys[T->t + i] = right->keys[i];
}
// 如果不是子树,需要拷贝结点
if (!left->leaf) {
for (i = 0; i < T->t; i++) {
left->childrens[T->t + i] = right->childrens[i];
}
}
// 合并后多了M/2个节点。
left->num += T->t;
btree_destroy_node(right);
// x 的key要前移
for (i = idx + 1; i < x->num; i++)
{
x->keys[i - 1] = x->keys[i];
x->childrens[i] = x->childrens[i + 1];
}
x->childrens[i + 1] = NULL;
x->num -= 1;
if (x->num == 0) {
T->root = left;
btree_destroy_node(x);
}
}
(2)B树的删除。
- 借位:如果子树关键字数量=M/2-1,需要借位,避免资源不足。 借不到就进行合并。
- 删除流程:B树可以删除的状态时直接删除;B树不可以删除状态时,先合并或借位,转换为B树可以删除的状态,再删除。
代码实现如下:
void btree_delete_key(btree *T, btree_node *node, KEY_VALUE key) {
if (node == NULL) return ;
int idx = 0, i;
while (idx < node->num && key > node->keys[idx]) {
idx ++;
}
if (idx < node->num && key == node->keys[idx]) {
if (node->leaf) {
for (i = idx;i < node->num-1;i ++) {
node->keys[i] = node->keys[i+1];
}
node->keys[node->num - 1] = 0;
node->num--;
if (node->num == 0) { //root
free(node);
T->root = NULL;
}
return ;
} else if (node->childrens[idx]->num >= T->t) {
btree_node *left = node->childrens[idx];
node->keys[idx] = left->keys[left->num - 1];
btree_delete_key(T, left, left->keys[left->num - 1]);
} else if (node->childrens[idx+1]->num >= T->t) {
btree_node *right = node->childrens[idx+1];
node->keys[idx] = right->keys[0];
btree_delete_key(T, right, right->keys[0]);
} else {
btree_merge(T, node, idx);
btree_delete_key(T, node->childrens[idx], key);
}
} else {
btree_node *child = node->childrens[idx];
if (child == NULL) {
printf("Cannot del key = %d\n", key);
return ;
}
if (child->num == T->t - 1) {
btree_node *left = NULL;
btree_node *right = NULL;
if (idx - 1 >= 0)
left = node->childrens[idx-1];
if (idx + 1 <= node->num)
right = node->childrens[idx+1];
if ((left && left->num >= T->t) ||
(right && right->num >= T->t)) {
int richR = 0;
if (right) richR = 1;
if (left && right) richR = (right->num > left->num) ? 1 : 0;
if (right && right->num >= T->t && richR) { //borrow from next
child->keys[child->num] = node->keys[idx];
child->childrens[child->num+1] = right->childrens[0];
child->num ++;
node->keys[idx] = right->keys[0];
for (i = 0;i < right->num - 1;i ++) {
right->keys[i] = right->keys[i+1];
right->childrens[i] = right->childrens[i+1];
}
right->keys[right->num-1] = 0;
right->childrens[right->num-1] = right->childrens[right->num];
right->childrens[right->num] = NULL;
right->num --;
} else { //borrow from prev
for (i = child->num;i > 0;i --) {
child->keys[i] = child->keys[i-1];
child->childrens[i+1] = child->childrens[i];
}
child->childrens[1] = child->childrens[0];
child->childrens[0] = left->childrens[left->num];
child->keys[0] = node->keys[idx-1];
child->num ++;
node->keys[idx-1] = left->keys[left->num-1];
left->keys[left->num-1] = 0;
left->childrens[left->num] = NULL;
left->num --;
}
} else if ((!left || (left->num == T->t - 1))
&& (!right || (right->num == T->t - 1))) {
if (left && left->num == T->t - 1) {
btree_merge(T, node, idx-1);
child = left;
} else if (right && right->num == T->t - 1) {
btree_merge(T, node, idx);
}
}
}
btree_delete_key(T, child, key);
}
}
int btree_delete(btree *T, KEY_VALUE key) {
if (!T->root) return -1;
btree_delete_key(T, T->root, key);
return 0;
}
六、完整代码
完整代码很长,已上传gitee,可点击链接进入查看。同时欢迎关注我的公众号《Lion 莱恩呀》,随时随地学习技术。
总结
B树是多叉树的一种,但B树不等于多叉树;B树的主要目的是降低层高。B树和B+树的区别在于B树的所有结点都是存储数据的;而B+树的内结点不存储数据,而是作为索引,数据存储在外结点;B+树更适合做磁盘索引,性能优于B树。
假设一颗M阶B树,它满足:
(1)每个结点至多拥有M颗子树;
(2)根结点至少拥有两颗子树;
(3)除了根结点以外,其余每个分支结点至少拥有M/2颗子树;
(4)所有叶子结点在同一层上;
(5)有K颗子树的分支结点则存在K-1个关键字,关键字按照递增顺序进行排序;
(6)关键字数量满足ceil(M/2)-1 <=n<=M-1。
另外,分裂只有在添加的时候才有;合并与借位只有在删除的时候有。


