关于模拟信号理想抽样和恢复sinc(x),使用matlab实现,加详细注释
有关对于信号的抽样和恢复问题
最近在学习数字信号处理这门课程,真的是头都要炸了,第一棘手的问题就是关于模拟信号的抽样,还有恢复问题
关于模拟信号的抽样
- 首先对于模拟信号的抽样是要对于频带受限的信号,存在一个最大上限频率
- 就是利用奈奎斯特抽样定理进行抽样
fs 作为抽样频率
关于模拟信号的抽样,抽样之后的信号的频谱是原模拟信号的频谱的以2pifs 为周期的周期延拓,幅值是以fs加权之后的幅值
通过matlab实验可以更加的直观的加深我们的理解
clear;
close all ;
clc;
fs = 10000 ; fs1 = 1000; fs2 = 400; fs3 = 200 ;
%求近似模拟信号的频谱
t = 0 : 1/fs : 0.1 ; %采集信号的长度为0.1秒
A = 444.128; a = 50*sqrt(2)*pi ; b = a ; %连续时间信号的参数
xa = exp(-a*t).*sin(b*t) ;
k = 0 : 511 ;
f = fs*k/512 ;
w = 2*pi*k/512 ;
%首先这里的e的指数部分,首先进行一次矩阵的相乘运算
%得到一个length(xa)*512的矩阵,其中的每一列对应的都是每一点的w值所对应的
%e的指数形式的在采集信号长度内的求和
%然后外部有进行一次矩阵的乘法运算
%得到一个1*512的矩阵,就是对应采样点的w(就是频率)所对应的值
Xa = xa*exp(-1i*[1:length(xa)]'*w) ; %求的近似模拟信号的频谱
%求抽样频率为1kHz时抽样信号的频谱
T1 = 1/fs1 ; t1 = 0 : T1 : 0.1 ; %采集信号的长度为0.1秒
x1 = exp(-a.*t1).*sin(b*t1) ; %1kHz的抽样序列x1(n)
X1 = x1*exp(-1i*[1: length(x1)]'*w) ; %x1(n)的512点DTFT
%求抽样频率为400Hz时抽样信号的频谱
T2 = 1/fs2 ; t2 = 0 : T2 : 0.1 ; %采集信号的长度为0.1秒
x2 = exp(-a.*t2).*sin(b*t2) ; %1kHz的抽样序列x2(n)
X2 = x2*exp(-1i*[1: length(x2)]'*w) ; %x2(n)的512点DTFT
%求抽样频率为200Hz时抽样信号的频谱
T3 = 1/fs3 ; t3 = 0 : T3 : 0.1 ; %采集信号的长度为0.1秒
x3 = exp(-a.*t3).*sin(b*t3) ; %1kHz的抽样序列x1(n)
X3 = x3*exp(-1i*[1: length(x3)]'*w) ; %x1(n)的512点DTFT
figure(1) ;
subplot(2, 2, 1) ;
plot(t, xa) ;
axis([0, max(t), min(xa), max(xa)]) ;
title('模拟信号') ;
xlabel('t(s)') ;
ylabel('Xa(t)') ;line([0, max(t)],[0,0]) ;
subplot(2, 2, 2) ;
plot(f, abs(Xa)/max(abs(Xa))); %这里进行归一化处理
title('模拟信号的幅度频谱') ;
axis([0, 500, 0, 1]) ;
xlabel('f(Hz)') ;
ylabel('|Xa(jf)|') ;
subplot(2, 2, 3) ;
stem(t1, x1, '.') ;
line([0, max(t1)], [0, 0]) ;
axis([0, max(t1), min(x1), max(x1)]) ;
title('抽样序列x1(n)(fs1=1kHz)') ;
xlabel('n') ;
ylabel('X1(n)') ;
f1 = fs1*k/512 ; %产生512个点
subplot(2, 2, 4) ;
plot(f1, abs(X1)/max(X1) ) ;
title('x1(n)的幅度谱') ;
xlabel('f(Hz)') ;
ylabel('|X1[jf]|');
figure(2) ;
subplot(2, 2,1) ;
stem(t2, x2, '.') ;
line([0, max(t2)], [0, 0]) ;
axis([0, max(t2), min(x2), max(x2)]) ;
title('抽样序列x2(fs2 = 400Hz)') ;
xlabel('n') ;
ylabel('X2(n)') ;
f = fs2*k/512 ;
subplot(2, 2, 2) ;
plot(f, abs(X2)/max(abs(X2))) ;
title('x2(n)的幅度谱') ;
xlabel('f(Hz)') ;
ylabel('|X2(jf)|') ;
subplot(2, 2,3) ;
stem(t3, x3, '.') ;
line([0, max(t3)], [0, 0]) ;
axis([0, max(t3), min(x3), max(x3)]) ;
title('抽样序列x3(fs3 = 200Hz)') ;
xlabel('n') ;
ylabel('X3(n)') ;
f = fs3*k/512 ;
subplot(2, 2, 4) ;
plot(f, abs(X3)/max(abs(X3))) ;
title('x3(n)的幅度谱') ;
xlabel('f(Hz)') ;
ylabel('|X3(jf)|') ;
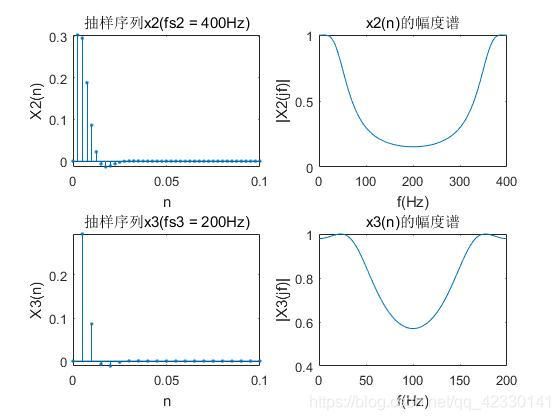
这里可以看到原信号的频谱在500hz之后,幅值基本上就减小到零了。然后观察使用的三种不同频率的抽样结果,可以看到使用抽样频率为1000的抽样后,频谱和原信号的频谱最契合,而其余两种的混叠失真比较严重,也验证了奈奎斯特抽样定理。
是指对于模拟信号,频谱可以延伸到无穷大,这里使用频率1000也是由混叠的,但是混叠的成分很小。
然后,在来看看使用内插函数的方法怎么实现对抽样信号的恢复
使用的函数为sinc(x) = sin(x)/x
有公式推导可以得到信号恢复的公式为:
这里需要注意的是,在使用matlab的sinc(x)的函数的时候,sinc(x) 代表的是 sin(pix)/(pix) ;
%这里使用频率为1000和频率为400的抽样信号进行
%对信号的恢复,观察两者之间的效果
%信号为444.128*exp(50*sqrt(2)*t)*sin(50*sqrt(2)*t))
clear ;
close all ;
clc ;
A = 444.128;
a = 50*sqrt(2)*pi ;
b = a ;
for k = 1:2
if k==1 Fs=400 ;
elseif k==2 Fs = 1000 ;
end
T = 1/Fs ; dt = T/3 ; %在每个抽样点前面插入两个值
Tp = 0.03; %重构的时间区间为0 - 0.03 ;
t = 0 : dt : Tp ; %生成时间序列
n = 0 : Tp/T ; %计算在重构的时间区间之内有多少个采样周期
%这里的减号前的一项完成将t序列复制length(n)的功能
%每一行都是从0-TP,步长为dt
%后一项时间n序列中的每一个值都复制一行0 - length(n)
%得到的两个矩阵的行和列是相等的
%ones(n,1)右乘1*m的矩阵是将右边的矩阵逐行复制n行
%ones(1,n)左乘m*1的矩阵是将左边的矩阵复制n列
%这里的结果产生的是(t-nT)/T
TMN = ones(length(n), 1) * t - n'*T*ones(1, length(t)) ; %生成TMN矩阵
x = A*exp(-a*n*T) .* sin(b*n*T) ;
%已知TMN是一个length(n)*length(t)的矩阵
%然后和exp(-a*n*T)这个1*length(n)的矩阵形成之后
%得到的是一个1*length(t)的矩阵
%就是每一个t所对应的值
xa = x*sinc(Fs*TMN) ;
subplot(2, 1, k) ;
plot(t, xa) ;
hold on
stem(x, n,'k') ;
axis([0, max(t), min(xa)-10 , max(xa)+10]) ;
st1 = sprintf('由Fs=%d', Fs);
st2 = 'Hz抽样序列x(n)重构产生的信号';
ylabel('x_a(t)') ;
st = [ st1, st2 ] ;
title(st) ;
xo = A*exp(-a.*t).*sin(b*t) ;
stem(t, xo, '.') ;
line([0, max(t)], [0,0]) ;
emax2 = max(abs(xa - xo) ) ;
end

在代码中加了大量的注释的地方也是我感觉自己在刚开始理解的时候不是很好理解的地方,希望对于也正在学习的你有帮助。
关于代码中的TMN矩阵的分析
关于ones(1,n)右乘和ones(n,1)左乘
在使用矩阵的时候这两个乘法应该是经常遇到的
假如ones(n,1)右乘一个1m的矩阵,那么矩阵相乘之后的结果肯定是一个nm的矩阵,这个矩阵的结果代表的含义就是将第二个矩阵复制m行。
假如ones(1,n)左乘一个m1的矩阵,那么得到的也是一个mn的矩阵,这代表着将这个列矩阵复制m列
我也是看了好多网上的解释,加上自己的理解写的小结,如果有错误,还望大佬指出。

