CSP-S 模拟赛 2023.7.20

CSP-S 模拟赛 $\mathrm{2023.7.20}$

第 $1$ 题 回文

题目

小 X 有 $N$ 个正整数 $a_1,a_2,...,a_N$。
他可以进行任意次操作，每次操作选取相邻的两个数 $a_x$ 和 $a_{x+1}$，将它们替换为一个数 $a_x+a_{x+1}$。例如，$[1,1,4,5,1,4]$ 可以在一次操作中变成 $[1,1,9,1,4]$。
小 X 想知道最少需要多少次操作，才能使得 $a$ 变为回文数组。如：$[1,2,3,2,1]$ 和 $[1,2,2,1]$ 是回文数组，而 $[1,1,4]$ 不是回文数组。

输入格式

第一行一个整数 $N$。
第二行 $N$ 个整数，依次表示 $a_{\mathrm{1...}N}$。

数据范围

对于 $30\%$ 的数据，$1⩽N⩽10$。
对于另外 $20\%$ 的数据，$1⩽N⩽100$。
对于 $100\%$ 的数据，$1⩽N⩽10^6,a_{\mathrm{1...}N}⩽1000$。

输出格式

一行一个整数表示答案。

样例

样例 $1$

输入

3
1 2 3

输出

1

解释

对 $a_1$ 和 $a_2$ 进行一次操作，$a=[3,3]$，是回文数组。

样例 $2$

输入

5
1 2 4 6 1

输出

1

解释

对 $a_2$ 和 $a_3$ 进行一次操作，$a=[1,6,6,1]$，是回文数组。

样例 $3$

输入

4
1 4 3 2

输出

2

解释

对 $a_1$ 和 $a_2$ 进行一次操作，$a=[5,3,2]$；
对 $a_2$ 和 $a_3$ 进行一次操作，$a=[5,5]$，是回文数组。

样例 $4$、$5$

点击下载

解法

如果 $a_l=a_r$，可以不考虑它们。
如果 $a_l<a_r$，合并 $a_{r-1}$ 和 $a_r$ 只会让右边更大，不能回文；所以合并 $a_l$ 和 $a_{l+1}$。
如果 $a_l>a_r$，合并 $a_l$ 和 $a_l+1$ 只会让右边更大，不能回文；所以合并 $a_{r-1}$ 和 $a_r$。
一直重复，直到 $l⩾r$ 即可。
时间复杂度 $\Theta (N)$。

代码

// 第一题：回文
// Created by 老徐 on 2023/7/21.
// 2023.7.20 测试
#include 

int N;
long long Arr[1000005];

int main() {
	std::cin >> N;
	for (int i = 1; i <= N; i++) {
		std::cin >> Arr[i];
	}
	int i = 1, j = N, Ans = 0;
	for (; i < j;) {
		if (Arr[i] == Arr[j]) {
			i++;
			j--;
		} else if (Arr[i] < Arr[j]) {
			Arr[i + 1] += Arr[i];
			i++;
			Ans++;
		} else if (Arr[i] > Arr[j]) {
			Arr[j - 1] += Arr[j];
			j--;
			Ans++;
		}
	}
	std::cout << Ans << '\n';
	return 0;
}

第 $2$ 题 配对

题目

小 X 有一个质数 $P$ 和一个非负整数 $K$。
小 Y 有 $N$ 个互不相同的非负整数 $a_1,a_2,...,a_N$。
小 X 和 小 Y 想贴贴，所以他们想知道有多少数对 $(i,j)$ 满足以下条件
$1⩽i<j⩽N,(a_i+a_j)({a_i}^2+{a_j}^2)\equiv K(\mathrm{mod}P)$

输入格式

第一行三个整数 $N,P,K$。
第二行 $N$ 个整数，依次表示 $a_{\mathrm{1...}N}$。

数据范围

对于 $30\%$ 的数据：$1⩽N⩽3000,2⩽P⩽3\times 10^5,0⩽K,a_i<P$。
对于 另外 $20\%$ 的数据：$1⩽N⩽3\times 10^5,2⩽P⩽10^9,K=0,0⩽a_i<P$。
对于 另外 $10\%$ 的数据：$1⩽N⩽3\times 10^5,2⩽P⩽10^9,K=1,0⩽a_i<P$。
对于 $100\%$ 的数据：$1⩽N⩽3\times 10^5,2⩽P⩽10^9,0⩽K,a_i<P$。

样例

样例 $1$

输入

3 3 0
0 1 2

输出

1

解释

$(2,3)$

样例 $2$

输入

6 7 2
1 2 3 4 5 6

输出

3

解释

$(1,5),(2,3),(4,6)$

样例 $3$、$4$、$5$、$6$

点击下载

解法

平方差公式：$a^2-b^2=(a+b)(a-b)$
观察式子，考虑左右同时 $\times (a_i-a_j)$，则根据平方差公式可得
$\equiv$ 左边 $=(a_i-a_j)(a_i+a_j)({a_i}^2+{a_j}^2)=({a_i}^2+{a_j}^2)({a_i}^2+{a_j}^2)={a_i}^4-{a_j}^4$
$\equiv$ 右边 $=K(a_i-a_j)=K{a}_i-K{a}_j$
将所有关于 $i$ 的项移到左边，所有关于 $j$ 的项移到右边得到 $K{a}_i-{a_i}^4\equiv K{a}_j-{a_j}^4(\mathrm{mod}P)$
问题就变成 $K\times a_i-{a_i}^4$ 相等的对数，开个 map存一下就解决了。
时间复杂度 $\Theta (N\log N)$，一重 for循环执行 $N$ 次，map内部复杂度 $\Theta (\log N)$。

代码

#include 
#include 

int N, Mod, Num;
int Arr[300005];
long long Ans;
std::map<int, int> Map;

int main() {
	std::cin >> N >> Mod >> Num;
	for (int i = 0; i < N; i++) {
		std::cin >> Arr[i];
		Arr[i] = int((long long) (Num) * Arr[i] % Mod) -
				 int((long long) (Arr[i]) * Arr[i] % Mod * Arr[i] % Mod * Arr[i] % Mod);
		Arr[i] = (Arr[i] % Mod + Mod) % Mod;
		Ans += Map[Arr[i]];
		Map[Arr[i]]++;
	}
	std::cout << Ans << '\n';
	return 0;
}

第 $3$ 题 地震恢复

题目

小 X 所在地区不幸地发生了地震，幸运的是人没事，但是他需要你帮助他规划地震后的修复工作。
形式化地说，小 $X$ 所在地区原本是一张 $N$ 个点 $M$ 条边的无向连通图，每个点 $Node$ 有点权 $NodeWeigh{t}_{Node}$，第 $i$ 条边有一个权值 $EdgeWeigh{t}_i$。由于地震影响，这 $M$ 条边都需要修复，未修复的边是无法连通的，这意味着这 $N$ 个点初始时互不连通。
第 $i$ 条边 $(Node1,Node2,Weight)$ 能被修复当且仅当 点 $Node1$ 所在的连通块的权值和 $+$ 点 $Node2$ 所在的连通块的权值和 $⩾$ $Weight$。
地震后的修复十分重要，所有你需要尽可能多地修复道路，但是为了效率，你不能修复一条无用的道路，即道路 $(Node1,Node2,Weight)$ 若被修复必须保证修复前 $Node1$ 和 $Node2$ 不连通。
请你在保证修复边尽可能长的情况下，构建出字典序最小的修复方案。一个修复方案指一个修复边的序列。

输入格式

第一行两个整数 $N,E$，分别表示点数和边数。

接下来一行 $N$ 个整数，第 i 个整数表示点 i 的权值 $NodeWeight$。

接下来 $E$ 行，每行三个整数 $Node1,Node2,Weight$，表示一条边 $(Node1,Node2,Weight)$。

数据范围

本题共 $25$ 个测试点。

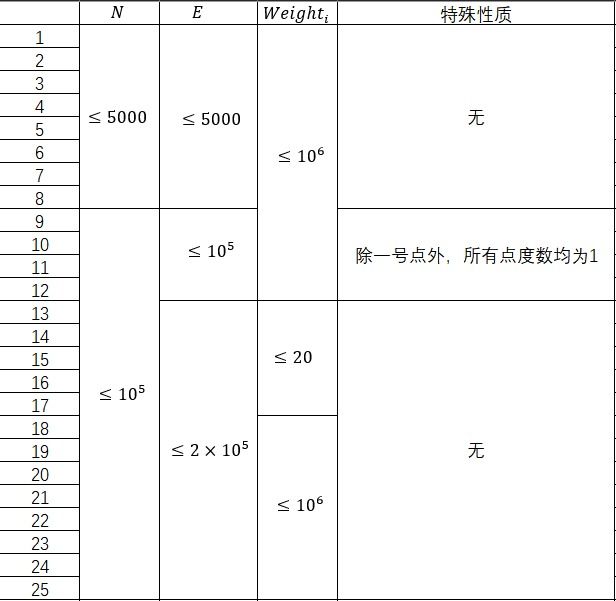
对于所有数据，保证给定的图连通且无自环，$0⩽NodeWeight[i]⩽10^6，1⩽Node1,Node2⩽N$。

输出格式

第一行一个整数 $K$，表示最多能修复的边数。
接下来一行 $K$ 个整数，表示一次修复的边的编号。

样例

样例 $1$

输入

5 5
1 1 1 1 1
1 2 3
2 3 2
3 4 1
4 5 1
5 1 1

输出

4
2 1 3 4

样例 $2$、$3$

点击下载

解法

$1$ 到 $8$ 测评点

贪心。
每次找到编号最小的能够修复的边并修复，时间复杂度 $\Theta (NE)$，正确性不难证明。
得分：32分

$9$ 到 $12$ 测评点

只有一号点度数不为 $1$，则这是一个菊花图，开个堆维护还没选的边即可。时间复杂度 $\Theta (N\log N)$
得分：16分

$13$ 到 $17$ 测评点

启发正确算法
每次合并两个连通块时，暴力合并还不能修复的出边，并将能修复的出边加入一个优先队列里，每次取出编号最小的修复并合并两个连通块即可。由于 $Weigh{t}_i⩽20$, 每条边最多被访问 $20$ 次就会变成可修复的边，所以时间复杂度为 $\Theta (N\log N+N\times Weigh{t}_i)$。
得分：20分

$18$ 到 $25$ 测评点

可以发现合并时，我们没有必要访问所有还不能修复的出边。具体来说，如果边 $i$ 还差权值 $k$ （还差指的是限制权值 $-$ 两端连通块目前的权值和），那么如果边两端的连通块权值增加都小于 $\frac{k}{2}$，那么这条边一定仍然无法修复。
那么我们就用一个优先队列维护连通块的所有出边，给每条边设置一个触发点 $\frac{k}{2}$。
每次合并两个连通块的出边，并对所有达到出发点的边进行一次 $Check$。

合并方法

出边少的连通块弹出所有出边，插入到出边较多的那个连通块。

如果一条边被 $Check$ 但是仍然不合法，那么就更新它的 $k$，并重新设置触发点。
可以发现，每条边只会被触发 $\Theta (\log Weigh{t}_i)$ 次，故总时间复杂度 $\Theta (N\log N+N{\log }^{2}Weigh{t}_i)$

代码

#include 
#include 
#include 
#include 

int N, M;

struct Node {
	int Id;
	int Limit;

	bool operator<(Node A) const {
		return Limit > A.Limit;
	}
} Nodes[100005];

int NodeWeight[100005], UFS[100005];
struct Edge {
	int Node1, Node2, Weight;
} Edges[200005];

int Find(int X) {
	if (UFS[X] == X) return X;
	return UFS[X] = Find(UFS[X]);
}

std::priority_queue<Node> Queue[100005];
std::priority_queue<int, std::vector<int>, std::greater<> > Tmp;

void Insert(int EdgeId) {
	int Root1 = Find(Edges[EdgeId].Node1), Root2 = Find(Edges[EdgeId].Node2);
	if (Root1 == Root2) return;
	if (NodeWeight[Root1] + NodeWeight[Root2] >= Edges[EdgeId].Weight) {
		Tmp.push(EdgeId);
		return;
	}
	int Diff = Edges[EdgeId].Weight - NodeWeight[Root1] - NodeWeight[Root2];
	Queue[Root1].push({EdgeId, NodeWeight[Root1] + (Diff + 1) / 2});
	Queue[Root2].push({EdgeId, NodeWeight[Root2] + (Diff + 1) / 2});
}

void Merge(int Node1, int Node2) {
	if (Queue[Node1].size() < Queue[Node2].size()) std::swap(Node1, Node2);
	while (!Queue[Node2].empty()) {
		Queue[Node1].push(Queue[Node2].top());
		Queue[Node2].pop();
	}
	UFS[Node2] = Node1;
	NodeWeight[Node1] = std::min(0x3F3F3F3F, NodeWeight[Node1] + NodeWeight[Node2]);
	while (!Queue[Node1].empty()) {
		Node Current = Queue[Node1].top();
		if (Current.Limit > NodeWeight[Node1]) break;
		Queue[Node1].pop();
		Insert(Current.Id);
	}
}

std::vector<int> Ans;

int main() {
	std::cin >> N >> M;
	for (int i = 1; i <= N; i++) {
		std::cin >> NodeWeight[i];
		UFS[i] = i;
	}
	for (int i = 1; i <= M; i++) {
		std::cin >> Edges[i].Node1 >> Edges[i].Node2 >> Edges[i].Weight;
		Insert(i);
	}
	while (!Tmp.empty()) {
		int Id = Tmp.top();
		Tmp.pop();
		int Node1 = Find(Edges[Id].Node1), Node2 = Find(Edges[Id].Node2);
		if (Node1 == Node2) continue;
		Ans.push_back(Id);
		Merge(Node1, Node2);
	}
	std::cout << Ans.size() << '\n';
	for (int i: Ans) std::cout << i << ' ';
	std::cout << '\n';
	return 0;
}

第 $4$ 题 好奇宝宝

题目

小 X 有 $N$ 个数 $a_1,a_2,...,a_N$。
好奇宝宝小 Y 不仅对小 $X$ 感兴趣，他也对这 $N$ 个数感兴趣。所以，他会进行 $M$ 次以下三种类型的操作之一
$1.$ $1LRX$ 将 $a_{[L...R]}$ 中每个元素二进制与一个数 $X$。
$2.$ $2LRX$ 将 $a_{[L...R]}$ 中每个元素二进制或一个数 $X$。
$3.$ $3LR$ 查询 $a_{[L...R]}$ 中的最小值。

输入格式

第一行两个整数 $N,M$
接下来一行 $N$ 个整数，表示 $a_{[\mathrm{1...}N]}$。
接下来 $M$ 题，每行表示一个操作。

数据范围

本题共 $25$ 个测试点。
$1$ 到 $5$：$1⩽N,M⩽1000$
$6$ 到 $12$：$1⩽N,M⩽10000$
$13$ 到 $20$：$1⩽N,M⩽100000$
$21$ 到 $25$：$1⩽N,M⩽500000$
对于所有数据，$0⩽a_i,X<2^{3}1$。

输出格式

对于每个操作 $3$，输出一行一个答案。

样例

样例 $1$

输入

5 4
4 5 1 2 7
3 2 4
1 1 3 3
2 2 5 2
3 2 5

输出

1
2

解释

第一个操作 $324$

数组为 $[4,5,1,2,7]$。
查询 $[5,1,2]$ 的最小值，为 $1$。

第二个操作 $1133$

数组为 $[0,1,1,2,7]$。

第三个操作 $2252$

数组为 $[0,3,3,2,7]$。

第四个操作 $325$

数组为 $[0,3,3,2,7]$。
查询 $[3,3,2,7]$ 的最小值，为 $2$。

样例 $2$、$3$、$4$

点击下载

解法

用线段树维护 $And,Or,Min$ 值，对于操作：
$1.$ $And(X)$，设当前点为 $This$，区间值分别为 $An{d}_{This},O{r}_{This},Mi{n}_{This}$:
如果 $X\&O{r}_{This}=O{r}_{T}his$，则该操作对当前区间无效；
如果 $O{r}_{This}\&X=An{d}_{This}\&X$，则该操作对当前区间的每个数影响都是一样的，可以打懒标记维护；
否则直接暴力递归。
$2.$ $Or(X)$，设当前点为 $This$，区间值分别为 $An{d}_{This},O{r}_{This},Mi{n}_{This}$:
如果 $An{d}_{This}\&X=X$，则该操作对当前区间无效；
如果 $O{r}_{This}\&X=An{d}_{This}\&X$，则该操作对当前区间的每个数影响都是一样的，可以打懒标记维护；
否则直接暴力递归。
分析一下时间复杂度：每次暴力递归都会使得当前区间内所有数的某一位相同，每个区间不同位的总数为 $\Theta (N\log N\log$ 值域$)$，时间复杂度就是 $\Theta (N\log N\log$ 值域$)$。

代码

#include 
#include 

int N, M;
int Arr[500005];

struct Node {
	int And, Or, Min, AndTag, OrTag;

	void AddAndTag(int X) {
		And &= X;
		Or &= X;
		Min &= X;
		AndTag = ((~AndTag) ? (AndTag & X) : (X));
		OrTag &= X;
	}

	void AddOrTag(int X) {
		And |= X;
		Or |= X;
		Min |= X;
		OrTag |= X;
		AndTag = ((~AndTag) ? (AndTag ^ (AndTag & X)) : (AndTag));
	}
} Tree[5000005];

int LChild(int Node) {
	return Node * 2;
}

int RChild(int Node) {
	return LChild(Node) + 1;
}

void Up(int Node) {
	Tree[Node].And = Tree[LChild(Node)].And & Tree[RChild(Node)].And;
	Tree[Node].Or = Tree[LChild(Node)].Or | Tree[RChild(Node)].Or;
	Tree[Node].Min = std::min(Tree[LChild(Node)].Min, Tree[RChild(Node)].Min);
}

void PushDown(int Node) {
	if (~Tree[Node].AndTag) {
		Tree[LChild(Node)].AddAndTag(Tree[Node].AndTag);
		Tree[RChild(Node)].AddAndTag(Tree[Node].AndTag);
	}
	if (Tree[Node].OrTag) {
		Tree[LChild(Node)].AddOrTag(Tree[Node].OrTag);
		Tree[RChild(Node)].AddOrTag(Tree[Node].OrTag);
	}
	Tree[Node].AndTag = -1;
	Tree[Node].OrTag = 0;
}

void BuildTree(int Node, int L, int R) {
	Tree[Node].AndTag = -1;
	Tree[Node].OrTag = 0;
	if (L == R) {
		Tree[Node].And = Tree[Node].Or = Tree[Node].Min = Arr[L];
		return;
	}
	int Mid = (L + R) / 2;
	BuildTree(LChild(Node), L, Mid);
	BuildTree(RChild(Node), Mid + 1, R);
	Up(Node);
}

void Query1(int Node, int TreeL, int TreeR, int InputL, int InputR, int X) {
	if ((Tree[Node].Or & X) == Tree[Node].Or) return;
	if (TreeL != TreeR) PushDown(Node);
	if (InputL <= TreeL && TreeR <= InputR) {
		if (TreeL == TreeR || (Tree[Node].Or & X) == (Tree[Node].And & X)) {
			Tree[Node].AddAndTag(X);
			return;
		}
	}
	int Mid = (TreeL + TreeR) / 2;
	if (InputL <= Mid) Query1(LChild(Node), TreeL, Mid, InputL, InputR, X);
	if (InputR > Mid) Query1(RChild(Node), Mid + 1, TreeR, InputL, InputR, X);
	Up(Node);
}

void Query2(int Node, int TreeL, int TreeR, int InputL, int InputR, int X) {
	if ((Tree[Node].And & X) == X) return;
	if (TreeL != TreeR) PushDown(Node);
	if (InputL <= TreeL && TreeR <= InputR) {
		if (TreeL == TreeR || (Tree[Node].Or & X) == (Tree[Node].And & X)) {
			Tree[Node].AddOrTag(X);
			return;
		}
	}
	int Mid = (TreeL + TreeR) / 2;
	if (InputL <= Mid) Query2(LChild(Node), TreeL, Mid, InputL, InputR, X);
	if (InputR > Mid) Query2(RChild(Node), Mid + 1, TreeR, InputL, InputR, X);
	Up(Node);
}

int Query3(int Node, int TreeL, int TreeR, int InputL, int InputR) {
	if (InputL <= TreeL && TreeR <= InputR) {
		return Tree[Node].Min;
	}
	int Mid = (TreeL + TreeR) / 2;
	PushDown(Node);
	if (InputL > Mid) return Query3(RChild(Node), Mid + 1, TreeR, InputL, InputR);
	if (InputR <= Mid) return Query3(LChild(Node), TreeL, Mid, InputL, InputR);
	return std::min(Query3(LChild(Node), TreeL, Mid, InputL, InputR),
					Query3(RChild(Node), Mid + 1, TreeR, InputL, InputR));
}

int main() {
	std::scanf("%d%d", &N, &M);
	for (int i = 1; i <= N; i++) std::scanf("%d", &Arr[i]);
	BuildTree(1, 1, N);
	for (int i = 0; i < M; i++) {
		int Op, L, R, X;
		std::scanf("%d%d%d", &Op, &L, &R);
		if (Op != 3) {
			std::scanf("%d", &X);
			if (Op == 1) Query1(1, 1, N, L, R, X);
			if (Op == 2) Query2(1, 1, N, L, R, X);
		} else {
			std::printf("%d\n", Query3(1, 1, N, L, R));
		}
	}
	return 0;
}