day57-day58【代码随想录】二刷数组

---

前言

1、螺旋矩阵||
2、螺旋矩阵
3、顺时针打印矩阵
4、在排序数组中查找元素的第一个和最后一个位置
5、有多少小于当前数字的数字
6、有效的山脉数组
7、平均等待时间
8、独一无二的出现次数

---

一、螺旋矩阵||（力扣59）

给定一个正整数 n，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

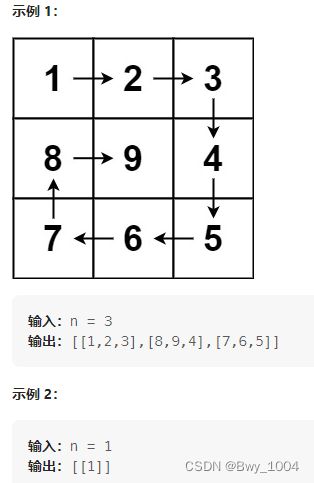
注意：循环次数，以及只有一个字符时的情况，或者转完一圈后，剩一个字符的情况。绕啊绕

class Solution {
    public int[][] generateMatrix(int n) {
        int loop = 0;//循环次数
        int[][] res = new int[n][n];
        int count =1; 
        int start =0;
        int i,j;
 
        while(loop++<n/2){ 
            for(j=start;j<n-loop;j++){
                res[start][j] = count++;
            }
            for(i=start;i<n-loop;i++){
                res[i][j] = count++;
            }
            for(;j>=loop;j--){
                res[i][j] = count++;
            }
            for(;i>=loop;i--){
                res[i][j] = count++;
            }
            start++;
        }
        if(n%2==1){  //既包括了一个字符的情况 也包括了转完一圈后剩一个字符的情况
            res[start][start]=count;
        }
        return res;
    }
}

方法二：
该方法可以作为一个模板

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] res = new int[n][n];
        int left = 0;
        int right = n-1;
        int top = 0;
        int bottom = n-1;
        int count = 1;

    res[0][0] =1;

        while(true){
            for(int i=left;i<=right;i++){
                res[top][i] = count++;
            }
            if(++top>bottom) break;

            for(int j=top;j<=bottom; j++){
                res[j][right] = count++;
            }
            if(--right<left) break;

            for(int i=right;i>=left;i--){
                res[bottom][i] = count++;
            }
            if(--bottom<top) break;

            for(int j=bottom;j>=top;j--){
                res[j][left] = count++;
            }
            if(++left>right) break;
        }
        return res;
    }
}

二、螺旋矩阵（力扣54）

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> res = new ArrayList<Integer>();

        int left = 0;
        int right = matrix[0].length-1;
        int top = 0;
        int bottom = matrix.length-1;

        while(true){
            for(int i=left;i<=right;i++){
                res.add(matrix[top][i]);
            }
            if(++top>bottom) break;

            for(int j=top;j<=bottom;j++){
                res.add(matrix[j][right]);
            }
            if(--right<left) break;

            for(int i=right;i>=left;i--){
                res.add(matrix[bottom][i]);
            }
            if(--bottom<top) break;

            for(int j=bottom;j>=top;j--){
                res.add(matrix[j][left]);
            }
            if(++left>right) break;
        }
        return res;

    }
}

三、顺时针打印矩阵（剑指 Offer29）

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。
与上一题的区别，这道题可以从0开始，也就是一开始的matrix={}
此时如果
int bottom = matrix.length-1;
int right = matrix[0].length-1;
放在开头就会报错

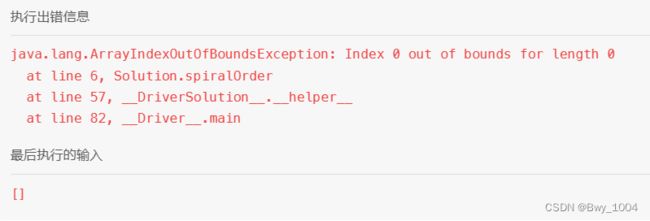
因此需要加一行：

if(matrix.length==0 ||matrix[0].length==0){
            return new int[0];
        }

class Solution {
    public int[] spiralOrder(int[][] matrix) {
        int top =0;
        int left = 0;
        
        if(matrix.length==0 ||matrix[0].length==0){
            return new int[0];
        }
        int bottom = matrix.length-1;
        int right = matrix[0].length-1;
        int[] res = new int[(bottom+1)*(right+1)];
        int k = 0;
        res[0]=1;

        while(true){
            for(int i=left;i<=right;i++){
                res[k++] = matrix[top][i];
            }
            if(++top>bottom) break;

            for(int j=top;j<=bottom;j++){
                res[k++] = matrix[j][right];
            }
            if(--right<left) break;

            for(int i=right;i>=left;i--){
                res[k++] = matrix[bottom][i];
            }
            if(--bottom<top) break;

            for(int j=bottom;j>=top;j--){
                res[k++] = matrix[j][left];
            }
            if(++left>right) break;
        }
        return res;
    }
}

四、在排序数组中查找元素的第一个和最后一个位置（力扣34）【二分查找】

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target，返回 [-1, -1]。

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int leftBorder = getLeftBoreder(nums,target);
        int rightBorder = getRightBoreder(nums,target);

        if(rightBorder==-2 || leftBorder==-2){
            return new int[]{-1,-1};
        }

        if(rightBorder-leftBorder>1){
            return new int[]{leftBorder+1,rightBorder-1};
        }
        else return new int[]{-1,-1};
    }
    public int getLeftBoreder(int[] nums, int target){
        int left = 0;
        int right = nums.length-1;
        int mid;
        int leftBorder=-2;
        while(left<=right){
            mid = (left+right)/2;
            if(nums[mid]>=target){
                right=mid-1;
                leftBorder = right;
            }else{
                left = mid +1;
            }
        }
        return leftBorder;
    }

    public int getRightBoreder(int[] nums, int target){
        int left = 0;
        int right = nums.length-1;
        int mid;
        int rightBorder=-2;
        while(left<=right){
            mid = (left+right)/2;
            if(nums[mid]<=target){
                left=mid+1;
                rightBorder = left;
            }else{
                right = mid -1;
            }
        }
        return rightBorder;
    }
}

五、有多少小于当前数字的数字（力扣1365）

给你一个数组 nums，对于其中每个元素 nums[i]，请你统计数组中比它小的所有数字的数目。
换而言之，对于每个 nums[i] 你必须计算出有效的 j 的数量，其中 j 满足 j != i 且 nums[j] < nums[i] 。
以数组形式返回答案。

找个桶，这个桶用来存放每个数字出现的次数，然后依次遍历这个桶，处理桶中的数据
比如 在案例中
bucket[1] =1
bucket[2] =2
bucket[3] =1
bucket[8] =1
遍历桶的时候 ：

		int count =0;
        for(int i=0;i<barcket.length;i++){
           int temp = barcket[i];
           barcket[i] = count;
           count +=temp;
        }

最后只取桶中我们需要的数据

class Solution {
    public int[] smallerNumbersThanCurrent(int[] nums) {
        //桶 存放数字n出现的次数
        int[] barcket = new int[101];
        for(int i:nums){
            barcket[i]++;
        }
        int[] res = new int[nums.length];
        int count =0;
        //处理桶
        for(int i=0;i<barcket.length;i++){
           int temp = barcket[i];
           barcket[i] = count;
           count +=temp;
        }
        int k=0;
        for(int i:nums){
            res[k++] = barcket[i];
        }
        return res;
    }
}

六、有效的山脉数组（力扣941）【双指针】

给定一个整数数组 arr，如果它是有效的山脉数组就返回 true，否则返回 false。
如果 arr 满足下述条件，那么它是一个山脉数组：
arr.length >= 3
在 0 < i < arr.length - 1 条件下，存在 i 使得：
arr[0] < arr[1] < … arr[i-1] < arr[i]
arr[i] > arr[i+1] > … > arr[arr.length - 1]

注意这个测试用例：

先上山， i=1;iarr[i-1];i++
如果 退出这个循环后 i依然等于1 或者i等于 arr.length时 说明上山上不动或者一次爬到终点两种情况 均return false

此时i指向最高点的下一位

再下山，;iarr[i];i++
如果退出循环后 i可以等于arr.length 说明下山成功 可以下到山脚
如果;iarr[i+1];i++ 退出循环后 i如果等于arr.length-1 这样子
就会出现测试用例的情况

class Solution {
    public boolean validMountainArray(int[] arr) {
        int i ;

        for(i=1;i<arr.length && arr[i-1]<arr[i];i++);
            //上山爬不动或者一次爬到终点
        if(i==1 || i==arr.length) return false;

        for(;i<arr.length-1 && arr[i]>arr[i+1];i++);
        return i==arr.length-1;
    }
}

七、平均等待时间（力扣1701）

有一个餐厅，只有一位厨师。你有一个顾客数组 customers ，其中 customers[i] = [arrivali, timei] ：
arrivali 是第 i 位顾客到达的时间，到达时间按 非递减 顺序排列。
timei 是给第 i 位顾客做菜需要的时间。
当一位顾客到达时，他将他的订单给厨师，厨师一旦空闲的时候就开始做这位顾客的菜。每位顾客会一直等待到厨师完成他的订单。厨师同时只能做一个人的订单。厨师会严格按照 订单给他的顺序 做菜

类似于先来先服务调度算法 ，先计算到达时间， 开始时间不一定等于到达时间，可能上一位顾客结束比较晚，那么开始时间就应该等到上一位顾客结束之后 start 和arrival应该取较大值，然后等待时间累加即可

class Solution {
    public double averageWaitingTime(int[][] customers) {
   
    int start=0;
    double wait =0;
        for(int[] customer:customers){
            int arrivali = customer[0];
            start =Math.max(start,arrivali);  //一定要取最大值 [5,2],[5,4]
            start +=customer[1];  //结束时间
            wait += start-arrivali; //等待时间总和
        }
        return wait/customers.length;
    }
}

八、独一无二的出现次数（力扣1207）

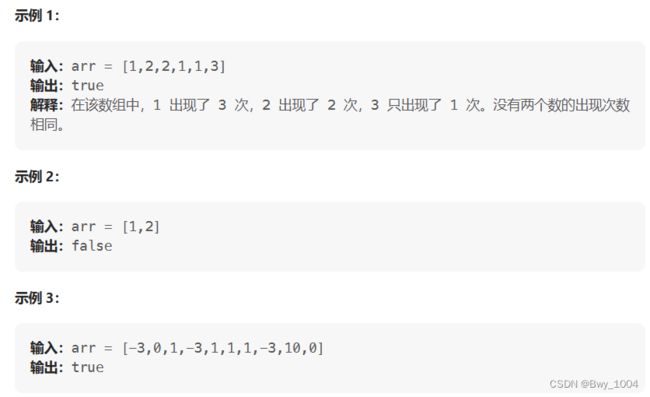
给你一个整数数组 arr，请你帮忙统计数组中每个数的出现次数。
如果每个数的出现次数都是独一无二的，就返回 true；否则返回 false。

class Solution {
    public boolean uniqueOccurrences(int[] arr) {
        HashMap<Integer,Integer> map = new HashMap<>();
        for(int i:arr){
            map.put(i,map.getOrDefault(i,0)+1);
        } 
        //遍历数组 看数组有没有重复的值
        //统计不同的出现次数的数目。如果不同的出现次数的数目等于不同数字的数目
        Set<Integer> times = new HashSet<Integer>();
        for(Map.Entry<Integer,Integer> x:map.entrySet()){
            times.add(x.getValue());
        }
        return times.size() == map.size();   
    }
}

---

每日一题：二进制数转字符串（力扣05.02）

二进制数转字符串。给定一个介于0和1之间的实数（如0.72），类型为double，打印它的二进制表达式。如果该数字无法精确地用32位以内的二进制表示，则打印“ERROR”。

class Solution {
    public String printBin(double num) {
        StringBuilder ans = new StringBuilder();
        ans.append("0.");
        while(num>0 && ans.length()<=32){
            num = num*2.0;
            if(num>=1){
                ans.append("1");
                num=num-1;
            }else{
                ans.append("0");
            }
        }
        return ans.length() <= 32 ? ans.toString() : "ERROR";
    }
}

每日一题：保证文件名唯一（力扣1487）

给你一个长度为 n 的字符串数组 names 。你将会在文件系统中创建 n 个文件夹：在第 i 分钟，新建名为 names[i] 的文件夹。
由于两个文件 不能 共享相同的文件名，因此如果新建文件夹使用的文件名已经被占用，系统会以 (k) 的形式为新文件夹的文件名添加后缀，其中 k 是能保证文件名唯一的 最小正整数 。
返回长度为 n 的字符串数组，其中 ans[i] 是创建第 i 个文件夹时系统分配给该文件夹的实际名称。

创建一个哈希表，遍历names数组，拿到name之后去哈希表中看看有没有出现过，如果没有 names数组不需要做任何操作，哈希表需要记录一下 此name出现的次数为1。如果出现过，首先先获取一下出现了多少次，假设gta出现了1次，注意：不能直接在出现次数上+1=2 gta(2)，而需要看看names中有没有这个次数 如果有 则次数需要继续++，并且需要修改map中该元素出现的次数。

class Solution {
    public String[] getFolderNames(String[] names) {
        Map<String,Integer> d = new HashMap<>();
        for(int i=0;i<names.length;i++){
            if(d.containsKey(names[i])){
                int k = d.get(names[i]);//获取出现的次数
                while(d.containsKey(names[i] + "(" +k+")")){
                    k++;
                }
                //更新值
                d.put(names[i],k);
                names[i] += "(" +k+ ")"; 
            }
            d.put(names[i],1);    
        }
        return names;
    }
}