【数据结构与算法】字符串匹配，BF算法和KMP算法，next数组求法
朴素的模式匹配算法
bf算法
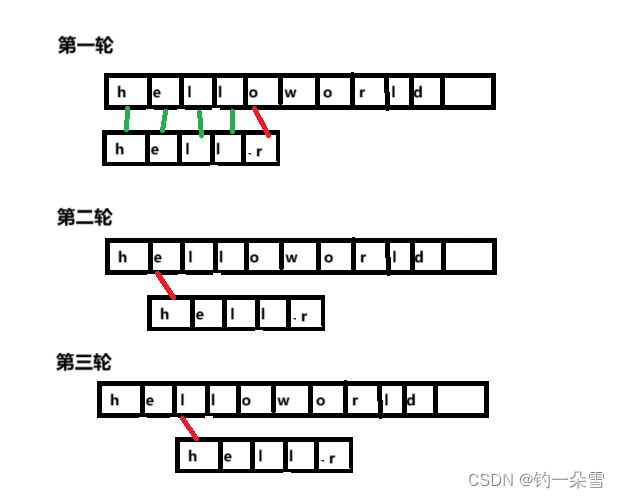
假设在主串S="helloworld"中找T="hellr"这个子串的位置
实现的思路如下
- 第一轮：子串中的第一个字符和主串中的第一个字符进行比较
- 如果相等，继续比较主串和子串中的第二个字符
- 如果不相等，进行第二轮比较
- 第二轮：子串中的第一个字符和主串中的第二个字符进行比较
- 如果相等则继续比较子串和主串的下一个字符。
- 如果不相等，这进行下一轮比较。
- 第N轮：同第二轮
如果主串中没有匹配的字符串就返回-1。
int bfFind(char*s,int slen,char*t,int tlen) {
//主串和子串的指针，i主串，j子串
int i, j;
//主串比子串小，匹配失败，curLenght为串的长度
if (slen< tlen)
return -1;
while (i < slen && j < tlen) {
//对应字符相等，指针后移
if (s[i] == t[j])
i++, j++;
else { //对应字符不相等
i = i -j + 1; //主串指针移动
j = 0; //子串从头开始
}
//返回子串在主串的位置
if (j >= tlen)
return (i -tlen);
else return -1;
}
}
KMP算法
KMP算法是一种对朴素模式匹配算法的改进，核心就是利用匹配失败后的信息，尽量减少子主串的匹配次数，其体现就是 主串指针一直往后移动，子串指针回溯。
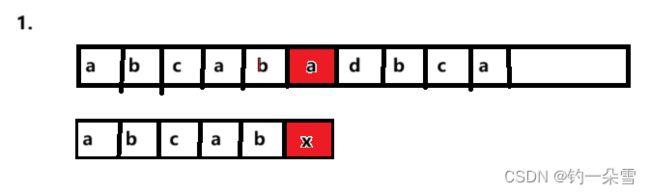
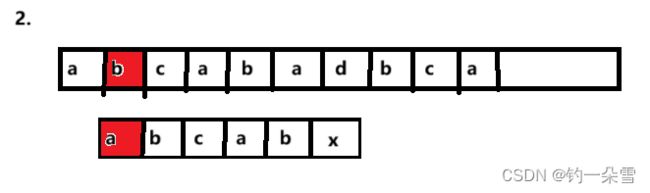
考虑这样的主串S="abcabadbca"和子串T=“abcabx”
如果采用朴素模式匹配算法的过程大致如下
-
第一个轮 主串S和子串T前五个字符匹配，第六个字符开始失配。
-
第二轮 按照BF算法，接下来匹配主串第2个字符和子串的第一个字符
-
第三轮
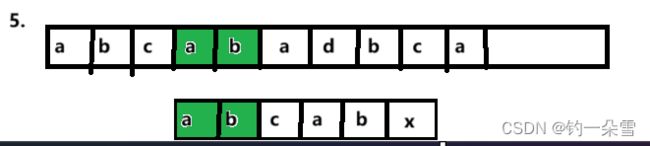
由S[0]==T[0],S[1]==T[1],S[2]==T[2],且T[0],T[1],T[2]互不相等，那么第二和第三轮比较是可以跳过的。
4. 第四轮
- 第五轮
由于子串T[0]==T[3],T[1]==T[4],根据第一轮的比较，T[0…1]==S[3…4],那么第四、第五轮比较是可以跳过的。 - 第六轮
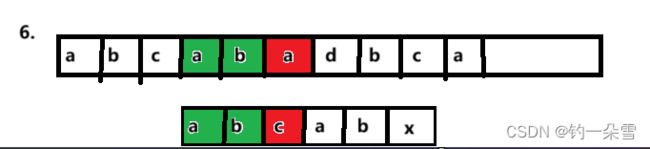
那么，采用KMP算法在第一轮失配后会直接进行第六轮的比较。那么在某一个字符处失配后，子串指针要移动到那一个位置？KMP算法还要求一个next数组，next数组给出了要移动到的位置。
next数组
next数组的公式
n e x t [ j ] = { − 1 当 j = 0 M a x ( k ∣ 1 < k < j 且 ′ p 0 ⋅ ⋅ ⋅ p k − 1 ′ = = ′ p j − k + 1 ⋅ ⋅ ⋅ p j − 1 ′ ) 0 其他情况 next[j]=\begin{cases} -1 & 当j=0 \\ Max(k|1
next数组的含义：next[j]表示T[j]字符前面的字符串中最大的公共前后缀的长度。
比如abcabx,这个字符串字符x前面的字符串abcab。
前缀集合:
{ a , a b , a b c , a b c a } \{ a,ab,abc,abca \} {a,ab,abc,abca}
后缀集合：
{ b , a b , c a b , b c a b } \{ b,ab,cab,bcab \} {b,ab,cab,bcab}
那么最长相等前后缀就是ab。
前缀不包含最后一个字符，后缀不包含第一个字符
next数组的求法
请先点击这里看看求next数组的代码，如果看不懂请回到这里。
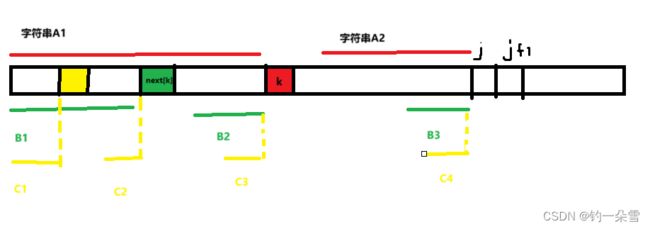
先看这个图，这个图表示的就是要查找的字符串，求next数组使用类似数学归纳法的三个步骤：
- 初始条件（next[0]=-1,k=-1,j=0;）
- 假设第j位和第j位前都求出来了
- 推论第j+1位
这个图可以得到的条件如下：
next[j]==k
next[k]==绿色块的索引
next[绿色块的索引]=黄色块的索引
- 由
next[j]==k这个条件，可以得到字符串A1==字符串A2 - 由
next[k]==绿色块的索引，可以得到B1==B2 - 由
next[绿色块的索引]=黄色块的索引，可以得到C1==C2 - 由1和2可以推出B1B2B3
- 由2和3可以推出C1C2C3,再结合4可以得到C1C2C3==C4
根据这些条件，接下来开始推导如果第j+1位失配时next[j+1]的值
已知A1==A2,那么A1和A2分别往后加一个字符是否会相等？
- 如果str[k]==str[j],显然A1和A2往后加一个字符会相等，这个时候next[j+1]的值就是
k+1 - 如果str[k]!=str[j],那么str从0到j位的最大前后缀就不可能是A1和A2了，那么接下来从B1和B3这两个前后缀入手。
B1和B3分别往后加一个字符是否会相等？
处理B1和B3是先要挪一下k的位置next[k]==绿色块的索引，令k=next[k]，也就是把k移到绿色块那里。
- 如果str[k]==str[j],显然B1和B2会往后加一个字符相等，这个时候next[j+1]的值就是k+1(next[j]+1)
- 如果str[k]!=str[j],那么str从0到j位的最大前后缀就不可能B1和B3了，那么接下来从C1和C4这两个前后缀入手······按照这个流程推导下去就可以把next[j+1]求出来了。（因为j+1位之前的next数组都已经假设求出来了，这个流程是一定会结束的）
在这个过程要考虑一个特殊情况，当k=-1的时候是不能继续的（也就是根本就没有相同的前后缀），这个时候next[j+1]=0。比如abaca这个串求最后一个a的next值
求next数组代码
根据这个过程给出的求next数组的代码。
点击这里转到代码解释
void Getnext(char*str,int strlen,int*next){
int j=0;
int k=-1;
next[0]=-1;
while (j<strlen)
{
if(k==-1||str[j]==str[k]){
++j;
++k;
next[j]=k;
}else{
k=next[k];
}
}
}
KMP算法的代码
int KMP(char*s,int slen,char*t,int tlen)
{
int next[255];
int i=0;
int j=0;
Getnext(t,tlen,next);
while(i<slen&&j<tlen){
if(j==-1||s[i]==t[j]){
i++;
j++;
}else{
j=next[j];
}
}
if(j>=tlen){
return i-tlen;
}
else{
return -1;
}
}