算法-动态规划-java

动态规划

动态规划的核心

哪些不记得过去的人，都注定要重蹈覆辙
（因为要记录过去的事情，所以是典型的空间换时间）

动态规划算法的两种形式

上面已经知道动态规划算法的核心是记住已经求过的解，记住求解的方式有两种：
①自顶向下的备忘录法 ②自底向上。
举一个最简单的例子，使用斐波那契数列来理解

首先使用递归的方法实现这个算法

public int fib(int n)
{
	if(n<=0)
		return 0;
	if(n==1)
		return 1;
	return fib( n-1)+fib(n-2);
}
//输入6
//输出：8

使用递归数，分析一下递归算法的执行流程，假如输入6，递归树如下：

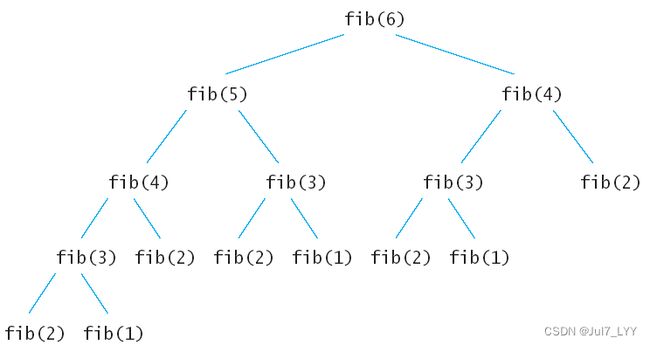
上面的递归树中的每一个子节点都会执行一次，很多重复的节点被执行，fib(2)被重复执行了5次。由于调用每一个函数的时候都要保留上下文，所以空间上开销也不小。这么多的子节点被重复执行，如果在执行的时候把执行过的子节点保存起来，后面要用到的时候直接查表调用的话可以节约大量的时间。下面就看看动态规划的两种方法怎样来解决斐波拉契数列数列问题。

①自顶向下的备忘录法

public class FibonacciMemoization {
    public static int Fibonacci(int n) {
        if (n <= 1)
            return n;
//这里为什么开辟空间的时候需要length+1，因为在求最优解的时候会用到Memo[0]
//到后边还有更清晰的图解
        int[] Memo = new int[n + 1];
        for (int i = 0; i <= n; i++)
            Memo[i] = -1;

        return fib(n, Memo);
    }

    public static int fib(int n, int[] Memo) {
        if (Memo[n] != -1)
            return Memo[n];

        Memo[n] = fib(n - 1, Memo) + fib(n - 2, Memo);

        return Memo[n];
    }

    public static void main(String[] args) {
        int n = 6;
        int result = Fibonacci(n);
        System.out.println("Fibonacci(" + n + ") = " + result);
    }
}

备忘录法也是比较好理解的，创建了一个n+1大小的数组来保存求出的斐波拉契数列中的每一个值，在递归的时候如果发现前面fib（n）的值计算出来了就不再计算，如果未计算出来，则计算出来后保存在Memo数组中，下次在调用fib（n）的时候就不会重新递归了。比如上面的递归树中在计算fib（6）的时候先计算fib（5），调用fib（5）算出了fib（4）后，fib（6）再调用fib（4）就不会在递归fib（4）的子树了，因为fib（4）的值已经保存在Memo[4]中。

②自底向上的动态规划（推荐使用）

备忘录法还是利用了递归，上面算法不管怎样，计算fib（6）的时候最后还是要计算出fib（1），fib（2），fib（3）…,那么何不先计算出fib（1），fib（2），fib（3）…,呢？这也就是动态规划的核心，先计算子问题，再由子问题计算父问题。

public class FibonacciDP {
    public static long calculateFibonacci(int n) {
        if (n <= 1) {
            return n;
        }

        long[] fibArray = new long[n + 1];
        fibArray[0] = 0;
        fibArray[1] = 1;

        for (int i = 2; i <= n; i++) {
            fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
        }

        return fibArray[n];
    }

    public static void main(String[] args) {
        int n = 6; // 想要计算的斐波那契数列的项数
        long result = calculateFibonacci(n);
        System.out.println("第 " + n + " 项斐波那契数列的值为: " + result);
    }
}

一般来说由于备忘录方式的动态规划方法使用了递归，递归的时候会产生额外的开销，使用自底向上的动态规划方法要比备忘录方法好。

更好的理解动态规划

经典例题：钢条分割

首先使用递归的方法实现这个算法

public static int cut(int []p,int n)
	{
		if(n==0)
			return 0;
		int q=Integer.MIN_VALUE;
		for(int i=1;i<=n;i++)
		{
			q=Math.max(q, p[i-1]+cut(p, n-i));	
		}
		return q;
	}

递归很好理解，如果不懂可以看上面的讲解，递归的思路其实和回溯法是一样的，遍历所有解空间但这里和上面斐波拉契数列的不同之处在于，在每一层上都进行了一次最优解的选择，q=Math.max(q, p[i-1]+cut(p, n-i));这个段语句就是最优解选择，这里上一层的最优解与下一层的最优解相关。

①自顶向下的备忘录法

public static int cutMemo(int []p)
	{
		int []r=new int[p.length+1];
		for(int i=0;i<=p.length;i++)
			r[i]=-1;						
		return cut(p, p.length, r);
	}
	public static int cut(int []p,int n,int []r)
	{
		int q=-1;
		if(r[n]>=0)
			return r[n];
		if(n==0)
			q=0;
		else {
			for(int i=1;i<=n;i++)
				q=Math.max(q, cut(p, n-i,r)+p[i-1]);
		}
		r[n]=q;
		
		return q;
	}

有了上面求斐波拉契数列的基础，理解备忘录方法也就不难了。备忘录方法无非是在递归的时候记录下已经调用过的子函数的值。这道钢条切割问题的经典之处在于自底向上的动态规划问题的处理，理解了这个也就理解了动态规划的精髓。

②自底向上的动态规划（推荐使用）

public static int buttom_up_cut(int []p)
	{
		int []r=new int[p.length+1];
		for(int i=1;i<=p.length;i++)
		{
			int q=-1;
			//①
			for(int j=1;j<=i;j++)
				q=Math.max(q, p[j-1]+r[i-j]);
			r[i]=q;
		}
		return r[p.length];
	}

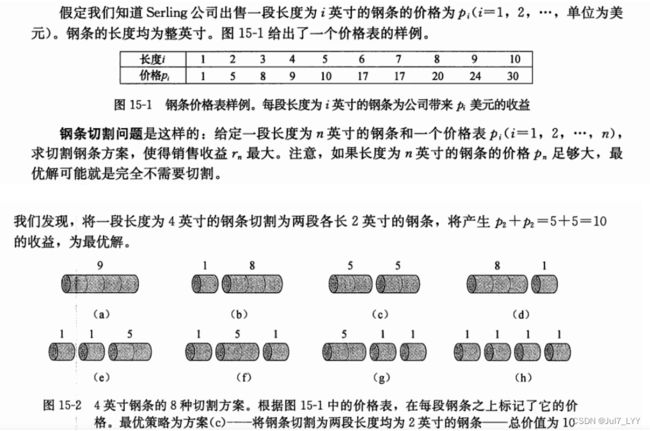
自底向上的动态规划问题中最重要的是理解注释①处的循环，这里外面的循环是求r[1],r[2]…，里面的循环是求出r[1],r[2]…的最优解，也就是说r[i]中保存的是钢条长度为i时划分的最优解，这里面涉及到了最优子结构问题，也就是一个问题取最优解的时候，它的子问题也一定要取得最优解。下面是长度为4的钢条划分的结构图。
从这个图也能理解，为什么r开辟空间的时候需要p.length+1，因为在求最优解的时候会用到r[0]